1. 引言
乳腺癌是威胁着全世界女性健康的一种常见恶性肿瘤。它已经成为目前世界上致死率较高的癌症之一 [1]。全球每年有52.2万人死于乳腺癌疾病,其中发达国家的发病率高于欠发达国家 [2]。雌激素受体活性α (Estrogen receptors alpha, Erα)是治疗乳腺癌的重要指标 [3],对于能够抑制其活性的化合物都有可能成为治愈乳腺癌的候选药物。药物不仅要有一定的活性,而且其药代动力学性质和安全性(简称ADMET)也必须得到一定的保障。
新药物的产生不可避免地需要兼顾建立化合物结构和生物活性模型和药代动力学性质的分类预测模型。这两个模型的建立也为后续优化药物生物活性和药代动力学性质打下了基础,使得研发人员在药物研发过程中具有更加灵活的自主性 [4]。
本文根据Erα拮抗药物的相关数据信息,利用基于遗传算法优化的神经网络建立化合物生物活性的定量预测模型,利用支持向量机SVM建立ADMET性质的分类预测模型,以此可作为优化Erα拮抗剂的生物活性和ADMET性质的预测的手段。本文数据来自2021年华为杯中国研究生数学建模竞赛D题,数据集为含有1974个化合物对Erα的生物活性数据、1974个化合物的729个分子描述符信息、1974个化合物的5种ADMET性质的数据。
2. ERα生物活性的定量预测模型
为了从1974个化合物中找到能够显著影响药物活性的化合物,首先对数据集进行预处理,将各个化合物的ERα生物活性绘制散点图,通过绘制散点图,可剔除与ERα生物活性无关,或影响极小的分子描述符,其部分分子描述散点分布图如图1所示,可以看出nAcid、ALogp2、nB等含量对化合物ER 生物活性并不敏感,应该予以剔除,对所有分子描述符进行处理后,再对化合物进行异常值处理,将不满足正态分布的自变量利用拉伊达准则去异,异常值处理流程图(图2)如下所示:
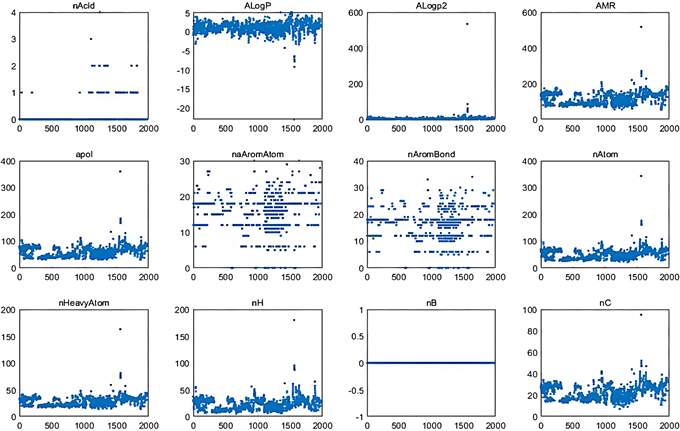
Figure 1. Scatter plot of partial molecular descriptor variables
图1. 部分分子描述符变量散点图
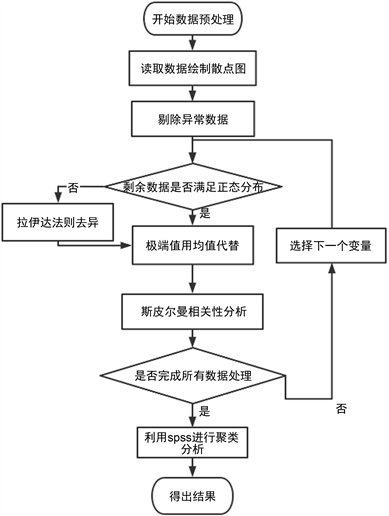
Figure 2. Abnormal data processing flow chart
图2. 异常数据处理流程图
2.1. 斯皮尔曼相关性分析及系统聚类
上述数据预处理中表明,分子描述符数据并不符合正态分布,根据这一特点,本题选择斯皮尔曼等级相关系数来分析各分子描述符对ERα生物活性的影响大小。
斯皮尔曼等级相关性系数反映两个变量之间的依赖性,用单调方程评价变量之间的相关性表示变量之间的关系强弱。其公式如下:
式中:
表示两个变量之间的差值,n表示样本大小。
由上述计算方法得出分子描述符变量ERα的生物活性值的相关性系数,如下图(图3)所示为相应的斯皮尔曼等级相关系数频率直方图:
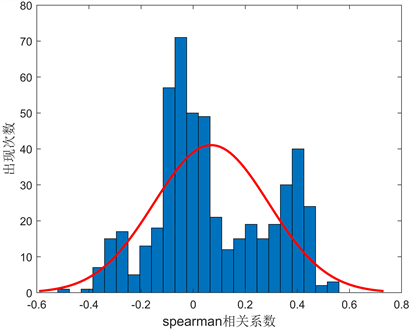
Figure 3. Spearman rank correlation coefficient frequency histogram
图3. 斯皮尔曼等级相关系数频率直方图
相关性显著性检验没有明确的规则限制,可以按照以下取值范围进行相关性强弱判断:
变量极强相关
变量强相关
变量中等相关
变量弱相关
变量极弱相关或者变量不相关
为了降低变量之间相关性,提升数据信息含量,在等级相关性分析的基础上,选出相关性系数绝对值大于0.4的前60个变量。再将这60个相关性系数较高的变量进行系统聚类分析,依据变量之间较大的距离作为类距将60个分子描述符变量分成20类,对每一类中的分子描述符按照斯皮尔曼等级相关性系数排名,选出每组中相关性最大一个变量。通过聚类分析和斯皮尔曼等级相关性排序,能得出对ERα生物活性影响最大且变量间相关性较小的前20个分子描述符,完成了从729个分子描述符到20个分子描述符的筛选降维,以此作为ERα生物活性预测模型的自变量,提高了模型训练的效率,且通过剔除无关变量,保证了预测、优化模型搭建的准确性,最后选出的二十个分子描述符变量如表1所示。

Table 1. 20 molecular descriptors after clustering optimization
表1. 聚类优化后的20个分子描述符
2.3. 基于遗传算法优化的BP神经网络预测模型
2.3.1. BP神经网络预测模型
BP神经网络是一种前馈神经网络,通过反向传播误差不断调整权重与偏置量,使得误差逐渐减小,得到一个接近正确值的最终结果。当训练集足够大、神经网络学习完成时得到的误差较小即可认为输入与输出之间的模型建立完成。本小节将训练集、测试集以7:3的比例进行分配,隐含层神经元个数设置为33个,其神经网络输入输出层关系图(图4)如下:
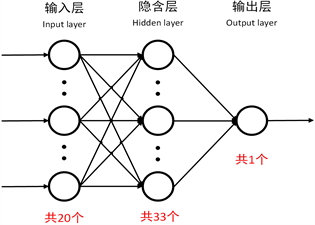
Figure 4. Neural network I/O layer diagram
图4. 神经网络输入输出层关系图
2.3.2. 遗传算法优化
往往BP神经网络容易陷入局部最优解,使得求解误差大,求解精度降低,遗传算法借鉴了生物进化的理论,将问题编码,类似于进化论里面的基因。而染色体则由基因组成。通过染色体的选择、变异、交叉的运算过程,多次迭代直至输出优质结果。这里使用遗传算法优化BP神经网络的初始权值和阈值,以神经网络输出的误差为种群适应度,可得到更为精确地拟合模型,图5为遗传算法优化的BP神经网络(GABP)的原理图。

Figure 5. Schematic of neural network optimized by genetic algorithm
图5. 遗传算法优化的神经网络原理图
经过多次试验,迭代数为200、种群数为30的模型训练效果较好,训练效率高。得到如下神经网络拟合图(图6)及回归分析图(图7):将两者结合起来不仅能够发挥遗传算法全局搜索的优势,而且保留了BP神经网络广泛映射的特点。
通常用神经网络结果的均方误差(MSE)和真实值R来判断神经网络模型的预测精度。均方误差(MSE)是预测值和真实值之差的平方和的平均值,MSE值越小,该模型的预测精度就越高。真实值R反映了预测模型的拟合程度,R越接近1效果越好。由模型预测结果图可以看出预测折线图和期望折线图的走势基本一致,并且数值距离较近。根据回归分析图(图7)可得误差分析结果可得训练集相关度R = 0.88468,测试集相关度R = 0.81827,总体相关度R = 0.79296,均方误差为0.5092,得到了较好的预测结果。
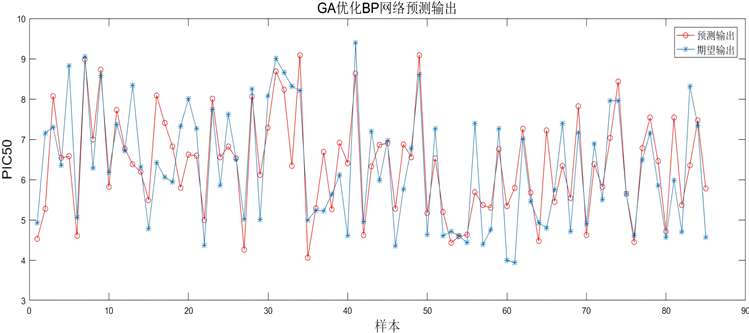
Figure 6. Fitting diagram of GABP neural network
图6. GABP神经网络拟合图
3. 基于支持向量机(SVM)的ADMET性质分类预测模型
本小节需要以化合物Caco-2、CYP3A4、hERG、HOB、MN的729个分子描述符为数据集,对药代动力学性质(ADMET)进行预测。其中5个药代动力学性质的取值都为0或1,是典型的二分类模型,支持向量机作为优秀的二分类器,其借助凸优化理论可以很好的解决二分法问题。
支持向量机的主要思想是:建立一个最优决策超平面,使得该平面两侧距离该平面最近的两类样本之间的距离最大化,从而对分类问题提供良好的泛化能力。对于一个多维的样本集,系统随机产生一个超平面并不断移动,对样本进行分类,直到训练样本中属于不同类别的样本点正好位于该超平面的两侧,满足该条件的超平面可能有很多个,SVM正式在保证分类精度的同时,寻找到这样一个超平面,使得超平面两侧的空白区域最大化,从而实现对线性可分样本的最优分类。
为了建立药代动力学性质与分子描述符之间的关系模型,首先对729个变量进行降维处理。由于本题的建模需要找出的是分子描述符之间分别与五个药代动力学性质的关系,这就使得在降维过程中必须考虑每个化合物对应的分子描述符与每个药代动力学性质的相关性。因此,针对五个药代动力学性质分别利用进行了5次相关性分析,下图分别是分子描述符对应的Caco-2、CYP3A4、hERG、HOB、MN的等级相关系数频谱图(图8),再将相关系数高的分子描述符进行聚类分析。
采用系统聚类分析,分成20个不同的类,并在每一个类中选取相关性系数较高的一个,选出的5组模型变量带入SVM中进行二分类。
对经过聚类分析优化得出的利用SVM支持向量机,可以得出五种ADMET性质(Caco-2,CYP3A4,hERG,HOB,MN)的测试集准确度分别为86.7%,95.2%,82.4%,90.4%,92.3%,利用SVM能够较为准确的预测所需的输出值。
4. 多目标优化及神经网络遗传算法函数极值寻优
4.1. 多目标优化问题
本小节优化目标为,寻找并阐述化合物的哪些分子描述符,能够使化合物对抑制ERα具有更好的生物活性,同时具有更好的ADMET性质(给定的五个ADMET性质中,至少三个性质较好),并给出分子描述符的取值或取值范围。
由于ADMET性质与药物活性指标pIC50为两个需要优化的条件,是多目标优化问题,通常来说多目标优化问题需要选择一个目标优先予以满足,已知pIC50值越大越好,而ADMET性质有五类性质,需要同时满足多项,参考多目标优化思想,以同时满足三个及以上ADMET性质的优化目标为优先目标。
为了验证该目标的正确性,本文通过MATLAB筛选出同时满足三个及三个ADMET性质的样本(“M”,“T”为毒性指标,为0时表现较好)。从1974个样本中,选出了632个样本作为满足多条ADMET性质条件的样本集。其中满足5个性质都好的样本有11个,满足4个性质都好的样本有177个,满足3个性质较好地有444个。可以看出,同时满足5个条件的样本个数只占样本的0.5%,满足4个性质的样本占8.9%,而满足3个性质的样本占22.4%,总体概率不到33%,而药物活性指标pIC50较好(假设pIC50 > 8)的概率达到了74.5%,由此可得出结论:应以满足ADMET性质为优先目标。从而将双目标优化问题转化为单目标优化问题。
4.2. 遗传算法函数极值寻优
本小节同样可以利用遗传算法进行神经网络遗传算法函数极值寻优,主要分为BP神经网络训练拟合和遗传算法极值寻优两步,神经网络训练拟合根据寻优函数的特点构建合适的BP神经网络,用非线性函数的输出数据训练BP网络,训练后的BP神经网络就可以预测函数输出。
化合物对Erα的生物活性值(用IC50表示,为实验测定值,单位是纳米(nm),值越小代表生物活性越大,对抑制Erα活性越有效);pIC50 (即IC50值的负对数,该值通常与生物活性具有正相关性,即pIC50值越大表明生物活性越高),以pIC50作为遗传算法极值寻优目标,把训练后的BP神经网络预测结果作为个体适应度值,通过选择、交叉和变异操作寻找函数的全局最优值及对应输入值。因为之前搭建的GABP神经网络预测模型对pIC50预测效果较好,可以利用第一小节选出的能影响pIC50变化的20个化合物,以及第二小节的GABP神经网络模型为本节的神经网络函数,把预测结果为遗传算法中的适应度,带入遗传算法寻优。
观察Erα的生物活性值IC50可知,实验中对IC50的测量值精度最高为0.1 nm,相应的其负对数pIC50的取值范围应为(0, 10],以适应度值越大为目标进行优选,神经网络训练结束后,可以利用遗传算法寻找该非线性函数的最大值。遗传算法的迭代次数是50次,种群规模是20,交叉概率为0.5,变异概率为0.2,采用浮点数编码,个体长度为20,优化过程中最优个体适应度值变化曲线如下图9所示,本小节优化原理图如图10所示。
遗传算法得到的最优个体适应度值(即pIC50活性)为9.93,最优个体为即为分子描述符最优取值,结果如下表2。
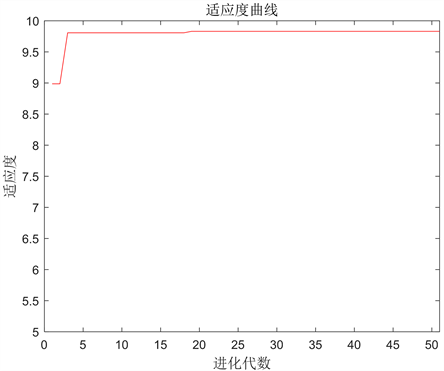
Figure 9. Genetic algorithm to optimize the fitness curve
图9. 遗传算法寻优适应度曲线

Table 2. Molecular descriptors and their value ranges
表2. 分子描述符及其取值范围
将得出的预测结果与实验中(pIC50 = 9.86)结果最好的化合物组合的取值范围,分别在同一量纲下进行对比,得到了如下图所示的实验最优解与预测解的对比折线图(图10),横坐标为20个分子描述符,纵坐标为其取值。从下图可以看出,预测结果与实验所得最优结果相差不大,且由于其差异性,得到了更优的预测值,体现了优化预测模型的正确性,及遗传算法寻优结果的准确性。
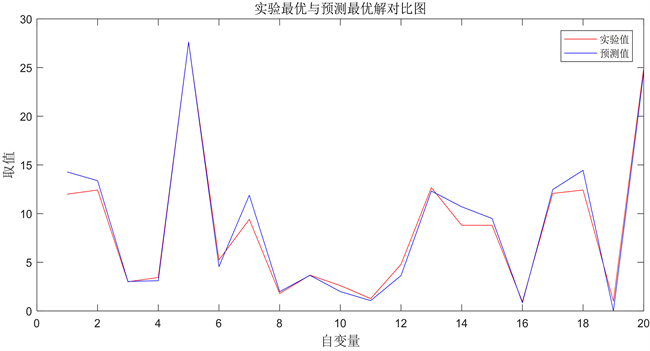
Figure 10. Comparison diagram of experimental optimal solution and predicted solution
图10. 实验最优解与预测解对比图
5. 总结与分析
本文根据通过系统聚类及相关性分析得出的20个主要分子描述符,利用遗传算法优化的BP神经网络模型对ERα的生物活性进行了预测,利用支持向量机模型对药物活性值(ADMET)进行了预测,得到了较好的优化效果,最后利用遗传算法优化GABP神经网络,以预测值pIC50为适应度目标,进行遗传算法寻优,找出了能同时满足pIC50值较大,ADMET性质较好的分子描述符取值范围。通过本文的模型搭建,能得出以下结论:
1) 从729个分子描述符中选择出了20个对ERα的生物活性影响较大的分子描述符为MDEC-23、MLogP、LipoaffinityIndex、nC等。
2) 通过建立遗传算法优化的GABP神经网络模型,对BP神经网络模型阈值进行择优,最后得到训练集相关度R = 0.88468,测试集相关度R = 0.81827,总体相关度R = 0.79296,均方误差为0.5092,得到了较好的预测结果。
3) 对于二分类目标,利用SVM支持向量机对ADMET五种性质进行预测,得出五种性质的预测准确率分别为86.7%,95.2%,82.4%,90.4%,92.3%。
4) 利用多目标优化思想,将多目标优化问题转换成单目标优化问题,再将前几小节选出的20个分子描述符和GABP神经网络模型,与遗传算法加以结合,以预测结果为适应度,得到50次迭代后的最优适应度(即pIC50活性)为9.93,其分子描述符的取值范围见表2。再将实验值与预测值进行对比,验证了遗传算法寻优模型的准确性。