1. 概述
近年来,随着互联网科学技术的兴起,每个行业的网络数据都变得无比庞大,其增长速度也呈指数级增长并且没有上限。特别是近几年大数据研究的高速发展,互联网中几乎每天都会产生很多新的来自于各个方面的数据,比如年度网络热词、电商平台和网红视频等等。这些数据来自各行各业,而又一同汇聚到互联网中。其关联关系网极其复杂。我们拥有海量的数据,但如何处理这些日渐庞大的数据量,然后高效地从这些数据中获取到我们所渴望的知识成为了所有人研究的热点。由此,数据挖掘应运而生。
数据挖掘 [1],旨在从海量的模糊随机数据中提取出人们事先不知道的有潜在价值的信息。数据挖掘不仅仅只是对数据进行简单的增删改查,它要做的是对这些海量的数据进行数据分析处理,挖掘出信息与信息之间的潜在关系。然后从多个层次、多个方面来进行研究。它可以对之前的数据进行统计分析,也可以基于当下的数据分析结果来对未来进行预测。数据挖掘在目前的大数据时代具有很大的应用价值。在数据挖掘领域中,关联规则挖掘 [2] 是一个非常值得关注的课题,它在教育、军工、电商等等领域都具有非常重要的研究意义。
然而关联规则挖掘领域中的最经典的几种传统算法对于当前大数据环境而言都具有局限性。比如Apriori算法,该算法思想简单,容易实现且扩展性高。但挖掘过程太过繁琐,频繁遍历中间结果集导致磁盘I/O过高,效率低下。另一种FP-growth算法速度快效率高,但可扩展性低,对于大型数据集来说经常会出现内存资源紧张的情况,容易导致内存溢出。针对以上算法的局限性,本文结合两种算法的优点,提出了基于深度递归与散列技术的改进Apriori算法。该算法参考FP-growth算法,结合深度递归思想避免了传统Apriori算法的频繁遍历过程,很大程度上减少了磁盘I/O,同时也保证了传统Apriori算法的可扩展性优点。改进算法参照散列技术改善存储结构,避免了FP-growth算法的内存溢出问题。以上改进解决了传统Apriori算法中固有的性能问题,并且让算法可以尽可能达到FP-growth算法层次的速度。
2. 关联规则挖掘算法
2.1. Apriori算法
关联规则挖掘的概念于1993年被Rakesh Agrawal提出 [3]。次年,R. Agrawal和R. Srikant在他们发表的论文 [4] 中提出了Apriori算法,该算法是关联规则挖掘领域中最经典的算法之一,它是一种先验性算法。传统Apriori算法通过多次的连接剪枝操作来遍历数据库,第一步从数据库中进行连接操作获取到低阶候选集,然后利用剪枝操作获取到候选集对应的频繁项集。第二步开始利用前一步获取到的低阶频繁项集再次进行连接操作得到中间候选集,然后再次利用剪枝操作获取到对应的二阶频繁项集。按此操作循环往复,直至获取到的频繁项集阶数达到研究人员要求的阶数停止。获取到频繁项集之后再利用其每一项的最小支持度来筛选出符合最小置信度的频繁项,按照置信度再获取到最终的强关联规则。该算法简单有效,但中间需要进行多次连接剪枝迭代,频繁进行磁盘I/O。当面临较大的数据集时,算法效率会大幅降低。优缺点明显。
2.2. FP-Growth算法
在2000年,由于当时Apriori算法缺点的局限性,Han与Pei等人提出了著名的FP-growth算法 [5],对于传统的Apriori算法来说,FP-growth算法相当于关联规则挖掘概念史上的一次技术革命,在算法效率上远超传统的Apriori算法。它基于树形数据结构,将所有的频繁项集用一棵树来表示,称为FP-tree。只需要对数据库进行两次扫描,避免产生大量的候选集。利用空间换时间,算法效率很高。但对内存不够友好,当面临大型数据集时,构建的FP-tree过于庞大,可能会导致内存溢出。
3. 基于递归的Apriori改进
3.1. 改进算法介绍
3.1.1. 改进算法分析
Apriori算法需要频繁遍历结果集,并且会产生大量的候选集,但是算法简单稳定易于实现,FP-growth算法可以不用产生大量的候选集,对数据库也只需要扫描两次即可。但对于大量的业务数据算法会产生一个体型庞大的FP树,该树存放于内存中,如果数据过大则可能会导致内存溢出。在算法挖掘过程中,中间出现错误之后对于问题追踪难度很大,虽然效率高但稳定性一般,本文提出基于递归的改进Ariori算法 [6] - [12],该算法结合Apriori算法和FP-growth算法的优点,避免两个算法的缺点,可以尽量少的遍历数据集,并且保证算法的稳定性。
Apriori改进算法描述如图1所示:
1) 给定支持度,置信度,以及最高获取到频繁项集的长度k。遍历事务数据集。支持度公式如下:
(1)
2) 遍历每一条数据,遍历过程中进行递归连接操作一次性生成所有的中间候选集。
3) 计算每一项中间候选集对应的支持度,运用散列技术将项集与其支持度按照映射关系存储在哈希存储中。存储完成之后以此候选集为基础连接下一个数据进入下一层递归操作。
4) 算法频繁递归生成所有的中间候选集,并按照候选集长度将其存储于事先设定好的哈希结构中。
5) 数据集的所有数据遍历完成后,得到所有的候选集,然后统一按照其支持度进行剪枝操作,剪枝完成之后即得到所有的频繁项集。
6) 利用最终结果中的频繁项集计算其置信度,然后将结果以映射结构存储于哈希结构中得到初步的关联规则。置信度公式如下:
(2)
7) 按照要求过滤掉不满足要求的弱关联规则,最终得到研究人员需要的强关联规则。

Figure 1. Description diagram of improved Apriori algorithm
图1. 改进Apriori算法描述图
3.1.2. 改进算法优势
本文提出的Apriori改进算法通过结合Apriori和FP-growth两个算法的优点并避免两个算法的缺点,在算法进行过程中获取事务集到中间候选集以及结果集的映射,再将映射存储在哈希存储中来进行数据挖掘,改进的算法共有以下优势:
8) 利用递归思想避免了传统的Apriori算法频繁遍历中间结果集和数据集的缺点,在第一次遍历数据集时就递归生成候选集,当所有的候选集生成之后统一利用支持度来进行剪枝,因为是根据初始数据集的每一条项集来生成的候选集,所以无需像传统Apriori算法那样将中间结果集与初始数据集进行比对计算支持度,对挖掘工作效率做出了比较大的改进。
9) 借鉴FP-growth算法的思想,尽量降低遍历数据集的次数。将递归产生的中间结果集存放于内存中。在内存资源充足的理想情况下,改进的算法可以做到只需遍历一次数据集即可完成数据挖掘工作。
10) 中间结果集运用哈希存储,哈希天然具有自动去重特性,这可以减少程序运行所需要的空间,降低算法的空间复杂度。
11) 由于改进算法存储了项目与事务之间的映射关系,在计算项目的支持度时,无需重新遍历原始数据库,只需取对应的事务集并做交集运算即可,有效提高了计算速度。
12) 使用哈希运算获得局部锁,可以提升算法在计算过程中的并行性能。当数据库中重复的事务较多时,计算事务权重能够大幅压缩事务集,从而提高计算速度。
13) 针对关联规则挖掘问题,对哈希函数进行优化,降低了哈希冲突的概率,同时对已计算出的项集对应的哈希值进行缓存,避免了重复计算。
3.2. 算法实例说明
以一实例来对该算法进行简单说明,如表1为事务数据库T:
1) 输入n = 3,指最多获取到频繁三项集,指定支持度Supmin = 3,置信度Confmin = 0.5。
2) 扫描数据库T,获取第一项TID为1的数据元素{1, 2, 5},进入第一层递归。
3) 递归生成第一项C1。
4) 将C1支持度加1,以映射的形式存储于哈希存储中,具体为:({1}, 1),哈希内部存储图如图2所示。
Figure 2. Frequent itemset hash storage graph
图2. 频繁项集哈希存储图
5) 由{1}作为输入进入第二层递归,连接第二个元素{2},生成C2。
6) 将C2支持度加1,以映射的形式存储于哈希存储中,具体为:({1, 2},1)。
7) 依次连接每一个元素,直至k达到要求。
8) 按照支持度进行剪枝操作,生成L1到Lk所有频繁项集,部分剪枝效果如图3所示。
9) 计算置信度,生成强关联规则,弱关联规则。得到结果为频繁二项集{1, 2}、{2, 4}为强关联规则,置信度分别为1, 0.6。

Figure 3. Frequent itemset pruning result graph
图3. 频繁项集剪枝结果图
4. 算法实验分析性能以及验证结果分析
为了比较基于递归散列改进的Apriori算法与经典Apriori算法的效率,更好证明改进后的算法相比于改进前的算法在性能及效率上的提升,因此进行了对比实验。在不同事务数以及不同最小支持度阈值的情况下,对比改进前的算法与改进后的算法在运行后产生频繁项集所需的时间。从而更加清晰直观有效的证明了改进后的算法在效率上有了相当大的提升。测试算法环境为:电脑Intel(R) Core(TM) i5-6200U,CPU为2.30 GHz,内存为12 G,操作系统为Windows10,编译软件为python3.8。
4.1. 不同事务数下对比结果分析
本实验所采用的数据集为国外某超市一段时间内共卖出的所有商品清单数据,共有9835条记录,我们总共将其分成7组数据,分别为500,1000,2000,3000,5000,7000以及9835条事务。按照不同的事务数量,测试在不同数据量和相同最小支持度阈值的情况下改进算法的效率。测试最小支持度阈值为15,测试结果如图4。
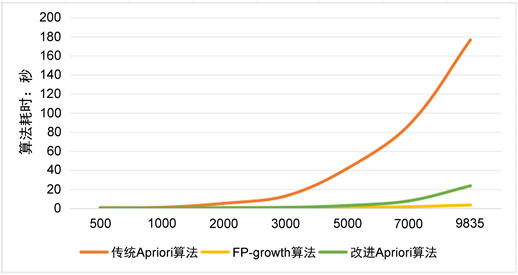
Figure 4. Comparison results of different transaction numbers
图4. 不同事务数比较结果图
由图4可知:事务数据量在500到2000条之间时,各个算法耗时相差不多,都保持在0.5秒左右,改进算法略高于另外两个传统算法;当事务数据量达到2000时,传统Apirori算法耗时变高,增长为4.998秒,FP-growth算法与改进Apriori算法相差不多,都为0.5秒左右;事务数据量达到3000时,传统Apriori算法耗时12.642秒,FP-growth算法耗时0.723秒,改进Apriori算法耗时0.786秒;事务量为5000时,传统Apriori算法耗时41.439秒,FP-growth算法耗时1.561秒,改进Apriori算法耗时2.771秒;事务量为7000时,传统Apriori算法耗时86.932秒,FP-growth算法耗时2.761秒,改进Apriori算法耗时7.615秒;事务量为9835时,传统Apriori算法耗时176.24秒,FP-growth算法耗时5.62秒,改进Apriori算法耗时23.369秒;由以上数据可知,无论是传统的Apriori算法还是改进之后的Apriori算法,在支持度阈值相同的情况下,事务数据的数量与算法运行的耗时是成正比的。然而相比较传统的Apriori算法,在事务数据量相等的情况下,改进后的算法运行起来效率要快很多。
4.2. 不同支持度下对比结果分析
本节目的是测试在相同事务数据量和不同最小支持度阈值的情况下改进算法的效率。我们将支持度分别设置为6个等级,分别为15、25、35、55、75和85来测试数据,实验将事务数据量固定为9835条。测试结果如图5。

Figure 5. Comparison results of different minimum support
图5. 不同最小支持度比较结果图
由图5可知:最小支持度阈值为15时,传统Apirori算法耗时176.24秒,FP-growth算法耗时5.62秒,改进Apriori算法耗时23.198秒;最小支持度阈值为25时,传统Apirori算法耗时86.784秒,FP-growth算法耗时2.371秒,改进Apriori算法耗时4.657秒;最小支持度阈值为35时,传统Apriori算法耗时53.977秒,FP-growth算法耗时1.731秒,改进Apriori算法耗时2.525秒;最小支持度阈值为55时,传统Apriori算法耗时30.555秒,FP-growth算法耗时1.233秒,改进Apriori算法耗时1.609秒;最小支持度阈值为75时,传统Apriori算法耗时26.01秒,FP-growth算法耗时1.049秒,改进Apriori算法耗时1.435秒;最小支持度阈值为85时,传统Apriori算法耗时21.804秒,FP-growth算法耗时1秒,改进Apriori算法耗时1.398秒;由以上数据可知,三种在事务数据量相同的情况下,算法耗时与最小支持度阈值成反比;与传统Apriori算法相比,改进后的算法运行起来效率要快很多,甚至在支持度阈值达到25之后算法耗时与FP-growth算法不相上下仅有毫秒之差。所以由以上结果可知,在不同支持度情况下,改进后的Apriori算法相比传统Apriori算法具有绝对优势。相比FP-growth算法则差距不多,在时间上能够达到接近FP-growth算法的速度,同时又保证了可扩展性。
5. 结束语
本文针对传统Apriori算法磁盘I/O过多且反复遍历中间结果次数过多导致执行速度太慢的问题,提出一种基于递归散列的Apriori改进算法。利用递归思想避免过多的磁盘I/O,再加上散列思想优化存储结构。而因为哈希天生的特性,我们还可以对所有的事务集去重压缩,然后统一进行加权计算得出最后的强关联规则。由于算法避免了过多的冗余计算,从而达到改进算法性能、提高算法效率的目的。本文实验结果表明,该改进后的算法可以在很大程度上降低算法运行过程中过多的磁盘I/O,减少运行耗时,相比较传统Apriori算法在性能上有很大提升,甚至在一定情况下算法耗时可以达到FP-growth算法的效果,且避免掉了FP-growth算法对于大量的业务数据算法可能会导致内存溢出,且中间出现错误之后对于问题追踪难度很大的问题。相较于传统的几种关联规则挖掘算法,本文提出的递归散列Apriori改进算法效率更高,可扩展性更高,磁盘I/O更少。然而因为是递归思想改进算法,会有一个伴生问题,就是随着一条事务数据的长度增加,递归的层数也会增加,最后导致栈内存溢出。对于此问题,该算法的下一步将会针对事务长度来进行改进,研究出能够分散事务的算法来进一步改善改进算法的效率。