一种兼容单相系统的通用软件锁相环设计

A General Software Phase-Locked Loop Compatible with Single-Phase System

摘要: 大功率车载充电机V2G工作模式，进行并网时，会存在单相三相系统切换的应用场景。本文提出一种通用型三相系统锁相环控制方法，该方法将单相系统视为三相不平衡故障的一种特例，基于移相控制的方式实现电压信号的正负序分离，设计出通用型软件锁相环，使其不仅能够适用于三相系统，也能够实现单相系统的兼容。最后通过模型仿真，针对三相电压不平衡和单相三相系统切换的应用场景，仿真验证了该锁相环设计的正确性。

Abstract: When the high-power onboard charger works as V2G mode, there will be an application scenario of single-phase three-phase system switching. In this paper, a general three-phase system phase- locked loop control method is proposed. This method regards the single-phase system as a special case of three-phase unbalanced fault, and realizes the positive and negative sequence separation of the voltage signal based on the phase-shift control method. The universal software phase- locked loop makes it not only suitable for three-phase systems, but also compatible with single- phase systems. Finally, through model simulation, for the application scenarios of three-phase voltage unbalance and single-phase three-phase system switching, the simulation verifies the correctness of the phase-locked loop design.

1. 引言

锁相环技术PLL (Phase-locked loop)是并网系统、大功率车载充电机OBC (On board charger)，尤其是V2G (Vehicle to grid)工作模式时的关键技术，精确快速检测电网电压相位信息是保证并网系统稳动态性能的重要前提。

对于三相并网系统，基于同步旋转坐标系的软件锁相法是当前采样最为广泛的锁相算法，但是当出现三相交流电压不平衡、畸变或者缺相时，该软件锁相法的锁相可靠性与精度仍然存在缺陷 [1]。针对电网电压进行正负序分量分离是普遍采用的一种方法，但这种方法将三相电压转换到两相坐标系后，采用低通滤波器、带通滤波器或陷波器等各类滤波器进行电网相位提取 [2] [3]。这种方法虽然理论可行，但是采用滤波器会带来大延迟，同时也存在一定的稳态误差。文献 [4] [5] 提出采用高阶滤波器的方法，可以具有更好的相位提取效果，但其实现算法也更复杂。基于积分器的软件锁相环不仅能解决电压不对称是的锁相问题而且对电压谐波不敏感，因此得到广泛应用，但是当电网中出现直流分量时，由于直流量的积分效果，将极大地损坏锁相环的效果 [6] [7]。为消除软件锁相振荡，文献 [8] 提出采用硬件过零点检测进行软件锁相误差校正的方法，增加了一定的系统成本。文献 [9] 提出扩展卡尔曼滤波器以提高锁相效果，但是其实现算法复杂，运算负担大，难以在现有运算器中实现。

为此，本文提出一种通用型三相系统锁相环控制方法，该方法将单相系统视为三相不平衡故障的一种特例，使得不仅能够适用于三相系统，针对国内更常见的单相交流充电桩也同样适用，从而实现单相系统锁相环控制的兼容。

2. 单相电压的同步旋转坐标等效模型分析

三相交流电压以对称的正序分量为主要成分，工频正序分量在同步旋转坐标系下，将被变换为已处理和分辨的直流信号，其中当Park变换用的相位信号与系统同步时，Q轴分量应为0，因而基于DQ同步旋转坐标的三相电压锁相环技术得到了广泛的应用 [10] [11]。在GB/T 18487中国电动汽车传导充电系统以及IEC 61851欧洲电动车辆充电系统中都包含了单相系统与三相系统的应用场合，只有在美国、日本等国家庭充电系统只需要满足单相充电，因此进行可靠的兼容单相系统的通用型锁相很有必要。按以上分析，如果将单相电压视为三相系统不平衡故障的一种特例，就可以在三相软件锁相环控制的基础上，实现单相系统的软件锁相控制。

2.1. 单相电压等效为三相不平衡故障的电压模型

在三相交流系统分析中，任意一组三相电压信号都可以被表示为对称的三相正序电压分量，对称的三相负序电压分量和对称的三相零序电压分量之和，而单相电压信号可以等效为三相电压不平衡的特例，如式(1)所示。

$\{\begin{array}{l}{u}_a\left(t\right)=A\sin \left(\omega t+\phi \right)\hfill \\ u_b\left(t\right)=0\hfill \\ u_c\left(t\right)=0\hfill \end{array}$ (1)

即单相电压可以表示为A相电压，而B相和C相电压为零，可组成一组三相不平衡电压。将此不平衡三相电压分解为正序电压分量、负序电压分量以及零序电压分量，如图1所示。

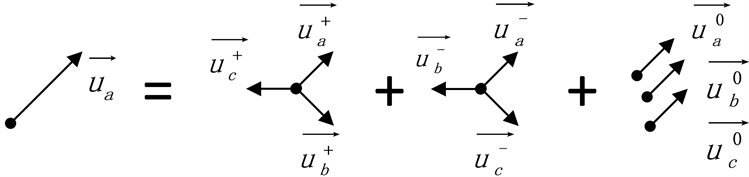
Figure 1. Three-phase unbalanced voltage model of single-phase grid voltage

图1. 单相电网电压等效三相不平衡模型

图中， $u_a^{+}$ 、 $u_b^{+}$ 、 $u_c^{+}$ 分别为ABC三相电压正序分量， $u_a^{-}$ 、 $u_b^{-}$ 、 $u_c^{-}$ 分别为ABC三相电压负序分量， $u_a^0$ 、 $u_b^0$ 、 $u_c^0$ 分别为ABC三相电压零序分量。因分解为对称的正序分量、负序分量、零序分量，所以有 $u_a^{+}=u_b^{+}=u_c^{+}$， $u_a^{-}=u_b^{-}=u_c^{-}$， $u_a^0=u_b^0=u_c^0$，则单相电压的数学公式如式(2)：

$\{\begin{array}{l}{u}_a=u_a^{+}{\text{e}}^{j0˚}+u_a^{-}{\text{e}}^{j0˚}+u_a^0{\text{e}}^{j0˚}\\ 0=u_a^{+}{\text{e}}^{j240˚}+u_a^{-}{\text{e}}^{j120˚}+u_a^0{\text{e}}^{j0˚}\\ 0=u_a^{+}{\text{e}}^{j120˚}+u_a^{-}{\text{e}}^{j240˚}+u_a^0{\text{e}}^{j0˚}\end{array}$ (2)

解方程组，有

$u_a^{+}=u_a^{-}=u_a^0=\frac{A}{3}$ (3)

即

$\left[\begin{array}{c}{u}_a\\ 0\\ 0\end{array}\right]=\frac{A}{3}\left[\begin{array}{c}{\text{e}}^{j0˚}\\ {\text{e}}^{j240˚}\\ {\text{e}}^{j120˚}\end{array}\right]+\frac{A}{3}\left[\begin{array}{c}{\text{e}}^{j0˚}\\ {\text{e}}^{j120˚}\\ {\text{e}}^{j240˚}\end{array}\right]+\frac{A}{3}\left[\begin{array}{c}{\text{e}}^{j0˚}\\ {\text{e}}^{j0˚}\\ {\text{e}}^{j0˚}\end{array}\right]$ (4)

可见，单相电压等效的不平衡三相电压的正负零序分量幅值相等，尤其是 $u_a^{+}$ 、 $u_a^{-}$ 、 $u_a^0$ 与 $u_a$ 的相位也相同，由此可知，A相电压的正序电压分量 $u_a^{+}$ 与单相电压信号 $u_a$ 相位相同。如果能够锁住A相电压的正序分量的相位，就能够实现单相电压 $u_a$ 的锁相。对于三相无中线系统，一般不考虑零序电压分量，而对于兼容单三相的系统，因存在中线，需要考虑零序电压分量的影响，可采用先将三相电压求和，得到零序分量，再在三相电压中减去零序分析的方法，得到仅存在正序电压分量和负序电压分量的电压信号，故以下不做零序分量的影响分析。

2.2. 双同步旋转坐标系下的特性分析

由以上分析，不考虑零序电压分量的影响，建立双同步旋转坐标系，这两个旋转坐标系的角速度相同，都为ω，但方向相反，如图2所示。

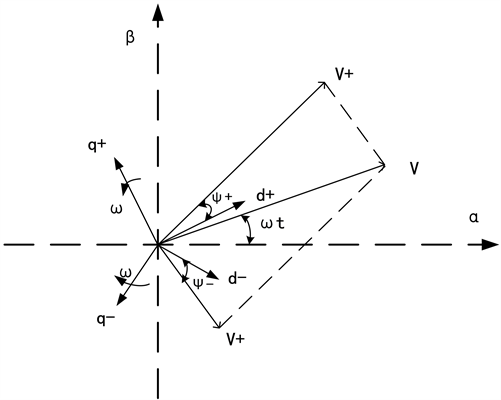
Figure 2. Double synchronous rotating coordinate

图2. 双同步旋转坐标系

将电压信号经过正序Park变换和负序Park变换后，d、q轴电压分量如式(5)和式(6)所示。

$\left[\begin{array}{c}{V}_d^{+}\\ V_q^{+}\end{array}\right]=\frac{A}{3}\left[\begin{array}{c}\cos \left(\phi \right)\\ \sin \left(\phi \right)\end{array}\right]+\left[\begin{array}{cc}\cos \left(-2\omega t\right)& -\sin \left(-2\omega t\right)\\ \sin \left(-2\omega t\right)& \cos \left(-2\omega t\right)\end{array}\right]\times \frac{A}{3}\left[\begin{array}{c}\cos \left(-\phi \right)\\ \sin \left(-\phi \right)\end{array}\right]$ (5)

$\left[\begin{array}{c}{V}_d^{-}\\ V_q^{-}\end{array}\right]=\frac{A}{3}\left[\begin{array}{c}\cos \left(-\phi \right)\\ \sin \left(-\phi \right)\end{array}\right]+\left[\begin{array}{cc}\cos \left(2\omega t\right)& -\sin \left(2\omega t\right)\\ \sin \left(2\omega t\right)& \cos \left(2\omega t\right)\end{array}\right]\times \frac{A}{3}\left[\begin{array}{c}\cos \left(\phi \right)\\ \sin \left(\phi \right)\end{array}\right]$ (6)

可见，正序分量在正序同步旋转坐标系上投影为直流分量，负序分量在负序同步旋转坐标系上投影为直流分量。而负序电压分量在正序同步旋转坐标系上投影为二倍频交流分量，同时正序电压分量也将在负序同步旋转坐标系上投影为二倍频交流分量。传统的控制器只能对直流量进行无静差控制，因此负序电压分量的存在，会对锁相环的输出产生很大的扰动。

3. 兼容单相系统的通用型锁相环控制设计

由以上分析，采用较低截止频率的低通滤波器LPF (low pass filter)，滤除二倍频及更高次交流分量，可以实现提取正序电压分量，但是较低的截止频率以牺牲锁相环控制的动静态性能为代价，其不能做到无差分离，且有可能破坏系统的稳定性，并不可取。本兼容的通用型锁相环控制方案，采用移相控制器来消除两倍于工频频率的扰动，此方案既能实现交流信号的滤除，也能保证锁相具有较好的动态性能。

3.1. 移相控制器实现正负序分离

将三相电压信号进行Park变换，得到d，q坐标系下包含正负分量的电压方程：

$\{\begin{array}{l}{u}_d=U^{+}\cos {\phi }^{+}+U^{-}\cos \left(2{\omega }_{0}t+{\phi }^{-}\right)\\ u_q=U^{+}\sin {\phi }^{+}-U^{-}\sin \left(2{\omega }_{0}t+{\phi }^{-}\right)\end{array}$ (7)

其中， ${\phi }^{+}$ 和 ${\phi }^{-}$ 为正、负序初始角。

将 $u_d$， $u_q$ 相移90˚，得到：

$\{\begin{array}{l}\overline{u_d}=U^{+}\cos {\phi }^{+}+U^{-}\sin \left(2{\omega }_{0}t+{\phi }^{-}\right)\\ \overline{u_q}=U^{+}\sin {\phi }^{+}+U^{-}\cos \left(2{\omega }_{0}t+{\phi }^{-}\right)\end{array}$ (8)

根据以上两式，可以进行正序分离， $u_d^{+}$， $u_q^{+}$ 为d，q坐标系下分解得到的正序分量：

$\{\begin{array}{l}{u}_d^{+}=U^{+}\cos {\phi }^{+}=0.5\left(u_d+u_q+\overline{u_d}-\overline{u_q}\right)\\ u_q^{+}=U^{+}\sin {\phi }^{+}=0.5\left(-u_d+u_q+\overline{u_d}+\overline{u_q}\right)\end{array}$ (9)

3.2. 移相控制器

移相控制器的基本原理可以表示为

$\{\begin{array}{l}\cos 2\omega t+\cos 2\omega \left(t-\frac{T}{4}\right)=0\\ \sin 2\omega t+\sin 2\omega \left(t-\frac{T}{4}\right)=0\end{array}$ (10)

在控制系统中，移相控制器须以离散形式表示，其离散结构图如图3所示。

Figure 3. Discrete block diagram of a phase-shift controller

图3. 移相控制器的离散框图

其中N为一个工频周期内电压信号的采样次数。

3.3. 通用性锁相环控制框图

基于以上分析，通用型锁相环控制框图如图4所示。

Figure 4. Control block of phase-locked loop

图4. 锁相环控制框图

基于对称分量提取的正序分量进行的电压锁相环，可以有效抑制不平衡电网中负序分量对锁相环控制的影响，但仍有一些缺点。当电网电压的频率发生变换时，对输入电压进行实时相移90˚时非常困难的，所以该方法对频率的适应性较差。同时，由于相移90˚，当电网相位或幅值发生突变时，整个锁相环的响应时间至少需要1/4个电网周期。

针对以上难点，可采用基于二阶广义积分器的90˚相角偏移特性，来实现两相正交信号，这一方案不仅可以实现90˚相角偏移，还可以滤除高次谐波，具有更高的系统带宽。二阶广义积分器如图5所示。

Figure 5. Phase-shift control based on second-order generalized integrator

图5. 二阶广义积分器为核心的移相控制

基于二阶广义积分器的软件锁相环控制框图如图6所示。

Figure 6. Software phase locked loop based on second order generalized integrator

图6. 基于二阶广义积分器软件锁相环

其中广义积分器用 $\int$ 表示，K值越小，滤波效果越好，但是系统响应速度变慢，折中滤波效果与响应带宽，常选取 $K=\sqrt{2}$。当电网电压出现三相不平衡跌落时，或者由三相电网切换到单相系统时，基于广义积分器的软件锁相环能够快速准确地获取电网电压正序分量的频率和相位信息，且当频率发生突变时，依旧能够快速获取电网电压正序分量的频率和相位信息。

4. 仿真与实验效果

为了验证所提出的通用软件锁相环控制的有效性，搭建了Simulink模型，在电网不平衡及单相三相系统切换的情形下进行锁相效果仿真。初始为三相平衡系统，在t = 0.05 s时出现B相电压跌落故障，电压跌落40%，C相电压出现电压突升，电压升至120%，在t = 0.09 s时电网电压恢复正常。仿真电压波形如图7所示。

Figure 7. The simulated three-phase voltage

图7. 仿真三相电压信号

锁相环仿真输出如图8所示。从仿真结果可以看出，采用以上锁相环控制，可以具有很好的动态效果，即使在t = 0.05 s以及t = 0.09 s仿真时刻，B、C相电压出现了突变，锁相环也能够快速进行相位锁定，图中的锁相环结果只出现了轻微的抖动，即可重新锁定。

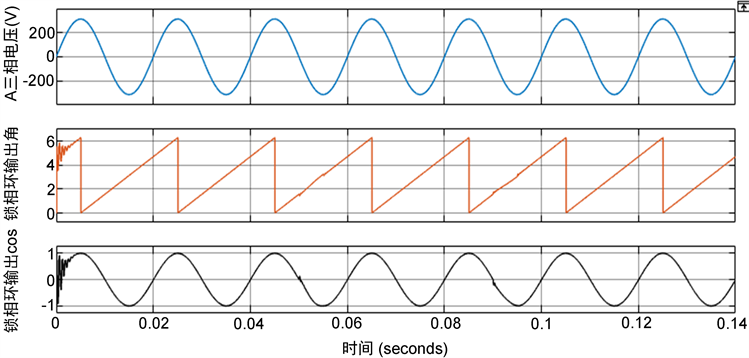
Figure 8. The output of the phase-locked loop

图8. 锁相环输出信号

为仿真验证单相三相系统的通用性，设定t = 0.05 s时，BC两相电压跌落为0，即切换为单相电压系统，t = 0.09 s时，BC相电压恢复，恢复为三相系统。电压波形如图9所示。

如图10所示为单相三相电压系统切换时锁相环的输出仿真。从仿真结果可以看出，当单相三相系统进行切换时，使用该通用锁相环，可以维持锁相环的稳定输出，即使出现的很小的偏差，也可以在1/4个周期内完成偏差的修正。

Figure 9. Single-phase three-phase voltage switching simulation waveform

图9. 单相三相电压切换仿真波形

Figure 10. Phase-locked loop output when single-phase three-phase voltage switching

图10. 单相三相电压切换锁相环输出

5. 结论

针对V2G等应用场合对单三相统一型锁相环的需求，本文在分析了单相的等效三相不平衡电压模型以及双同步旋转坐标系下的特性后，基于移相控制方式实现电压信号的正负序分离理论，提出了兼容单相系统的通用型软件锁相环理论。最后，针对三相不平衡和单三相系统切换的应用场景进行仿真，证明该通用型软件锁相环既适用于三相电压不平衡系统，又适用于单相三相经常切换的系统，且该方法锁相精度高，响应快，具有较强的实际应用价值。