具有工作休假和休假中断的M/M/1重试排队系统策略分析

Equilibrium of M/M/1 Retrail Queue System with Working Vacations and Vacation Interruption

摘要: 本文对具有工作休假和休假中断的M/M/1重试排队进行了研究。在队列中，顾客根据服务台是否被占用，服务台是否休假的情况，选择是否进入重试空间。通过对重试系统进行拟生灭过程研究并利用矩阵几何解法求出系统的性能指标，给出了顾客均衡和最优进队策，并给出均衡策略和最优策略下的社会均衡收益和社会最优收益。通过数值算例，比较了不同信息水平下的策略和收益。

Abstract: This paper studies M/M/1 retrail queue with working vacations and vacation interruption. In the queue, customers choose whether to enter the retrial orbit according to whether the server is oc-cupied and whether the server is on vacation. By studying the quasi-birth-death process of the retrail system and using the matrix geometric solution to obtain the performance index of the system, the customer equilibrium and the optimal queue strategy are given, and the social equi-librium income and social optimal income under the equilibrium strategy and optimal strategy are given. Through numerical examples, strategies and benefits under different information levels are compared.

1. 引言

在过去的几十年中Naor [1] 对客户的平衡和社会最优排队策略进行了深入研究，重试和休假的排队系统也随之发展。重试排队的通用模型、方法、结果、示例和应用可以在Artalejo和Corral以及Tian和Zhang中找到 [2] [3]。Wang，Zhang和Huang研究了在N策略下的重试排队的策略分析和优化 [4]。近年来，Li和Tian首先在文 [5] 中介绍，并研究了带有工作休假和假期中断的M/M/1排队，当系统在工作休假期服务完一个顾客后，若发现系统中仍有顾客，此时，系统中止休假，进入正常的服务状态，否则继续休假。Wang和Zhang考虑了单工作休假的马尔可夫队列中的均衡策略 [6]。此外，一旦系统的某些索引，例如：客户数量，在工作休假期间达到一定的价值。可以假设休假中断是在服务完成瞬间发生的。休假排队模型在计算机系统、通信系统和管理工程等领域都有重要的应用。对于假期中断模型，而后李继红、李文焘和田乃硕研究了带有部分工作休假和休假中断的M/M/c排队 [7]。在M/M/1重试队列中，Do研究了具有工作休假和恒定重试率的均衡客户行为 [8]。在离散时间下，重试空间的休假中断和工作休假的策略分析问题和可以参考Tao Li的文献 [9]。Li，Liu和Wang研究了在GI/M/1重试排队中带有启动期的单重工作休假和休假中断模型和在GI/M/1重试排队中带有伯努利策略的工作休假和休假中断模型 [10]。

2. 模型描述

在本文中，我们考虑具有工作休假和休假中断的M/M/1的重试排队，设：新顾客的到达形成强度为 $\lambda$ 的泊松过程。当系统不在休假时的服务速率为 $\mu$ 的指数分布。如果服务台忙，到达顾客可能会加入到无限大的重试空间，当重试空间不为空时，重试遵循速率为 $\alpha$ 的Posion过程。服务规则为FCFS。

如果重试空间上没有任何顾客，则单个服务台在客户离开系统时开始工作休假。休假时间服从参数 $\theta$ 的指数分布。在休假期间，占用服务台的顾客以速率 $\eta$ 接受服务( $\eta <\mu$ )，在服务完成的瞬间，服务器将停止休假。

设 $I\left(t\right)$ 为t时刻重试空间中的顾客数， $J\left(t\right)$ 为t时服务台的状态.在单一服务台的条件下有四种可能的状态如下：

$J\left(t\right)=\{\begin{array}{l}0,时刻服务台处于休假过程且服务台未被占用,\\ 1,时刻服务台处于休假过程且服务台正被占用,\\ 2,时刻服务台处于工作状态且服务台未被占用,\\ 3,时刻服务台处于工作状态且服务台正被占用.\end{array}$

所有的顾客都遵循一个混合的策略“当服务台的状态为 $j\left(j=0,1,2,3\right)$ 时，顾客选择进入系统的概率为 $q_j$ ”。假设到达时间、重试时间、服务时间、休假时间是相互独立的。

假定顾客到达时自己决定是否进入排队．一旦进入排队，中途退出是不允许的，每一个顾客完成服务都会有一个收益R，同时，当顾客进入系统，顾客需要因在系统中逗留(包括在重试空间中逗留和服务区域内逗留)而产生的一个单位时间的等待费用C。

拟生灭过程模型

当遵循混合策略“当服务台的状态为 $j\left(j=0,1,2,3\right)$ 时，顾客选择进入系统的概率为 $q_j$ ”时， $\{I\left(t\right),J\left(t\right)\}$ 是状态空间 $\Omega =\{\left(i,j\right),j\ge 0,i=0,1,2,3\}$ 的马尔科夫过程。令 ${\lambda }_v=\lambda q_0$， ${\lambda }_b=\lambda q_2$。

按字典顺序排列上述状态，则无穷小生成元矩Q阵被写成如下的分块三对角矩阵

$Q=\left(\begin{array}{cccc}{A}_0& C& & \\ B& A& C& \\ & & \ddots & \ddots \end{array}\right),$

由于矩阵Q的分块结构，称 $\{I\left(t\right),J\left(t\right)\}$ 为QBD过程。

3. 稳态性能分析

因为矩阵D可约，在文献 [11] 中的定理7.3.1中给出QBD过程的正常返条件，经过行列变换后，QBD是正常返的当且仅当

$v\left(\begin{array}{cc}0& \alpha \\ 0& 0\end{array}\right)e>v\left(\begin{array}{cc}0& 0\\ 0& \lambda q_3\end{array}\right)e,$

其中 $e={\left[\begin{array}{cccc}1& 1& \cdots & 1\end{array}\right]}^{\text{T}}$，v是 $\{\begin{array}{l}v\left(\begin{array}{cc}-{\lambda }_b-\alpha & {\lambda }_b+\alpha \\ \mu & -\mu \end{array}\right)=0\\ ve=1\end{array}$ 的解。

故QBD是正常返的当且仅当 $\alpha \mu >\left({\lambda }_b+\alpha \right)\lambda q_3$。

定理1 如果 $\alpha \mu >\left({\lambda }_b+\alpha \right)\lambda q_3$，则拟生灭过程 $\{Q\left(t\right),J\left(t\right)\}$ 的稳态分布可以表示为

$\{\begin{array}{l}{\pi }_{k0}=0,k\ge 1\\ {\pi }_{k1}={\pi }_{01}{r}_1{}^k,k\ge 0\\ {\pi }_{k2}={\pi }_{01}\left(r_2{r}_1{}^{k-1}\text{+}\frac{r_3{r}_4}{r_5-r_1}\left(r_5{}^{k-1}-r_1{}^{k-1}\right)\right)+{\pi }_{03}{r}_4{r}_5{}^{k-1}=0,k\ge 1\\ {\pi }_{k3}={\pi }_{01}\frac{r_3}{r_5-r_1}\left(r_5{}^k-r_1{}^k\right)+{\pi }_{03}{r}_5{}^k,k\ge 0\end{array}$

证明 使用 [11] 中的矩阵几何解法，有

${\pi }_k={\pi }_0{R}^k,k\ge 1$

其中

$B\left[R\right]=\left(\begin{array}{cc}{A}_0& C\\ B& RA+B\end{array}\right)$, $R=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& r_1& r_2& r_3\\ 0& 0& 0& 0\\ 0& 0& r_4& r_5\end{array}\right)$.

$r_1=\frac{\lambda q_1}{\lambda q_1+\eta +\theta }$, $r_2=\frac{\lambda q_1}{\alpha }$, $r_3=\frac{\lambda q_1\left(\alpha \theta +\alpha \lambda q_1+\eta {\lambda }_b+\theta {\lambda }_b+\lambda q_1{\lambda }_b\right)}{\alpha \mu \left(\lambda q_1+\eta +\theta \right)}$, $r_4=\frac{\lambda q_3}{\alpha }$, $r_5=\frac{\lambda q_3\left({\lambda }_b+\alpha \right)}{\alpha \mu }$.

由正规化条件

$\{\begin{array}{l}{\pi }_0\left(A_0+RB\right)=0,\\ {\pi }_0{\left(I-R\right)}^{-1}e=1.\end{array}$

得到

$\{\begin{array}{l}{\pi }_{00}=\frac{\eta +\theta +\lambda q_1}{\left(\frac{1}{1-r_1}+\frac{r_3+r_3{r}_4-r_2\left(-1+r_5\right)}{\left(-1+r_1\right)\left(-1+r_5\right)}-\frac{\left(\theta +\alpha r_2\right)\left(1+r_4\right)}{\left(\mu +\lambda q_3-\alpha r_4\right)\left(-1+r_5\right)}+\frac{\eta +\theta +\lambda q_1}{{\lambda }_v}\right){\lambda }_v},\\ {\pi }_{01}={\left(\frac{1}{1-r_1}+\frac{r_3+r_3{r}_4-r_2\left(-1+r_5\right)}{\left(-1+r_1\right)\left(-1+r_5\right)}-\frac{\left(\theta +\alpha r_2\right)\left(1+r_4\right)}{\left(\mu +\lambda q_3-\alpha r_4\right)\left(-1+r_5\right)}+\frac{\eta +\theta +\lambda q_1}{{\lambda }_v}\right)}^{-1},\\ {\pi }_{03}=\frac{\theta +\alpha r_2}{\left(\mu +\lambda q_3-\alpha r_4\right)\left(\frac{1}{1-r_1}+\frac{r_3+r_3{r}_4-r_2\left(-1+r_5\right)}{\left(-1+r_1\right)\left(-1+r_5\right)}-\frac{\left(\theta +\alpha r_2\right)\left(1+r_4\right)}{\left(\mu +\lambda q_3-\alpha r_4\right)\left(-1+r_5\right)}+\frac{\eta +\theta +\lambda q_1}{{\lambda }_v}\right)}.\end{array}$

令 $p_j={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\pi }_{k,j}}$ 为系统在状态j时的概率，可以得到服务台忙的概率为

$P_b=p_1+p_3=P\left\{J=1\right\}+P\left\{J=3\right\}=\frac{1-r_5+r_3}{\left(1-r_5\right)\left(1-r_1\right)}{\pi }_{01}+\frac{1}{1-r_5}{\pi }_{03}.$

服务台空闲的概率是

$P_f=p_0+p_2=P\left\{J=0\right\}+P\left\{J=2\right\}={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\pi }_{k0}}+{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\pi }_{k2}}=1-P_b.$

设L为重试空间上的顾客数，得

$\begin{array}{c}E\left[L\right]={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}k\left({\pi }_{k0}+{\pi }_{k2}\right)}+{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}k\left({\pi }_{k1}+{\pi }_{k3}\right)}\\ ={\pi }_{00}+{\pi }_{01}\frac{\left(r_1+r_2\right){\left(1-r_5\right)}^2+r_3{r}_4\left(2-r_1-r_5\right)+r_3\left(1-r_1{r}_5\right)}{{\left(1-r_1\right)}^2{\left(1-r_5\right)}^2}+{\pi }_{03}\frac{r_4+r_5}{{\left(1-r_5\right)}^2}.\end{array}$

设 $L_s$ 为系统中的顾客数量，则有

$E\left[L_s\right]={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}k\left({\pi }_{k0}+{\pi }_{k2}\right)+{\displaystyle \underset{k=0}{\overset{\infty }{\sum }}\left(k+1\right)\left({\pi }_{k1}+{\pi }_{k3}\right)}}=E\left[L\right]+P_b$

顾客在到达时发现服务台处于状态j的平均逗留时间 $T\left(j,q_1,q_3\right)$ 可以表示为

$T\left(0\right)=\frac{\mu +\theta }{\left(\eta +\theta \right)\mu },$

$T\left(1,q_1\right)=\frac{\theta +\mu }{\mu \left(\eta +\theta \right)}+\frac{{\lambda }_b+\alpha +\mu }{1-r_1},$

$T\left(2\right)=\frac{1}{\mu },$

$T\left(3,q_1,q_3\right)=\frac{1}{\mu }+\frac{{\lambda }_b+\alpha +\mu }{\alpha \mu }\left({\pi }_{01}\frac{r_3}{{\left(r_5-r_1\right)}^2}+{\pi }_{03}\right)\left(\frac{1}{1-r_5}-{\pi }_{01}\frac{r_3}{{\left(1-r_1\right)}^2}\right)\frac{\left(1-r_1\right)\left(1-r_5\right)}{{\pi }_{03}\left(1-r_1\right)+{\pi }_{01}{r}_3}.$

因此，当服务台在状态j时到达时，决定加入系统的客户的预期净利润为

$S_e\left(j,q_1,q_3\right)=R-CT\left(j,q_1,q_3\right),\left(j=0,1,2,3\right)\text{.}$

4. 完全不可视的情形的均衡策略和社会最优解

假设顾客不知道服务台是否在忙或是否在休假，此时顾客进入系统的混合策略是：客户进入系统的概率为 $q_j=q\left(i=1,3\right)$，在这种情况下，顾客的有效到达率是 ${\lambda }^{*}=\lambda q$。存在一个唯一得混合纳什均衡策略，顾客以 $q_e$ 的概率进入队列。

设W为顾客重试空间内的等待时间，因此根据Little’s公式，有

$E\left[W\right]=E\left[L\right]/\lambda q.$

则顾客在到达时决定进入服务器的平均逗留时间为

$E\left[W_s\right]=E\left[L_s\right]/\lambda q,$

因此，该顾客决定进入系统的净收益为

$S_e\left(q\right)=R-CE\left[W_s\right],$

社会最优解为

$S_{soc}\left(q\right)=\lambda q\left(R-CE\left[W_s\right]\right).$

通过社会收益最大化可以得到顾客的最优进队概率 $q^{\text{*}}$，令x是 ${S^{\prime }}_{soc}\left(q\right)=0$ 的解，则 $q^{*}=\max \left\{0,\min \left(x,1\right)\right\}$。

5. 数值分析

在完全不可见的情况下，图1~5为顾客均衡进队概率和最优进队概率。不同参数对顾客的均衡进队概率 $q_e$ 和最优进队概率 $q^{*}$ 的影响，在图1和图2中显示服务回报R和休假时的服务速率 $\eta$ 越大，进队概率越大。在图3和图4中显示随着休假率 $\theta$ 和重试率 $\alpha$ 的越大，顾客进队概率越大，这是因为，随着休假期时间的减少和重试率的增大，服务员可以更快的进入忙期，因此可以有更多的顾客可以进入系统。

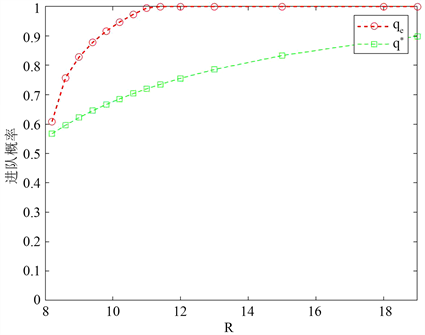
Figure 1. Probability of entering the system $C=1,\alpha =2,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

图1. 进队概率 $C=1,\alpha =2,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

Figure 2. Probability of entering the system $C=1,\alpha =2,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

图2. 进队概率 $C=1,R=9,\alpha =2,\lambda =0.6,\mu =1,\eta =0.1$

Figure 3. Probability of entering the system $C=1,R=9,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

图3. 进队概率 $C=1,R=9,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

Figure 4. Probability of entering the system $C=1,R=9,\alpha =2,\lambda =0.6,\mu =1,\theta =0.1$

图4. 进队概率 $C=1,R=9,\alpha =2,\lambda =0.6,\mu =1,\theta =0.1$

在完全不可见的情况下，研究了不同参数对顾客的均衡收益和最优收益的影响。在完全不可见排队中，顾客的均衡策略为 $q_e$，顾客遵循均衡策略时，收益用 $S_{soc}\left(q_e\right)$ 表示。顾客遵循最优策略 $q^{*}$ 时，收益用 $S_{soc}\left(q^{*}\right)$ 表示。在完全不可见排队中，顾客均衡收益和最优收益的数值分析具体算例如图5~8所示。

Figure 5. Social equilibrium benefit and optimal benefit $C=1,\alpha =2,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

图5. 社会均衡收益与最优收益 $C=1,\alpha =2,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

Figure 6. Social equilibrium benefit and optimal benefit $C=1,R=9,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

图6. 社会均衡收益与最优收益 $C=1,R=9,\lambda =0.6,\mu =1,\theta =0.1,\eta =0.1$

Figure 7. Social Equilibrium Benefit and Optimal Benefit $C=1,R=9,\lambda =0.6,\mu =1,\theta =0.1$

图7. 社会均衡收益与最优收益 $C=1,R=9,\lambda =0.6,\mu =1,\theta =0.1$

Figure 8. Social Equilibrium Benefit and Optimal Benefit $C=1,R=9,\alpha =2,\lambda =0.6,\mu =1,\eta =0.1$

图8. 社会均衡收益与最优收益 $C=1,R=9,\alpha =2,\lambda =0.6,\mu =1,\eta =0.1$

6. 定价策略

在完全不可视排队中，服务员对于进入系统的顾客费用为 $\rho$，则顾客的均衡策略满足 $R-\rho -CE\left(W_s\right)=0$。服务员的收益 ${\Pi }_s=\lambda q\rho$。顾客满足均衡收益时

$\rho =R-CE(\; W\; s\; )$

令上式和 $S_{soc}\left(q\right)$ 对比发现 ${\Pi }_s=S_{soc}\left(q\right)$。因此，我们可以通过让系统收取一定的费用促使顾客以最优策略 $q^{*}$ 进入系统，同时也使服务员的收益最大化。同时，最优策略 $q^{*}$ 也是顾客得均衡策略，最优定价为 ${\rho }^{\text{*}}=R-CE\left(W_s\left(q^{*}\right)\right)$，服务员收益最大化为 ${\Pi }_s=S_{soc}\left(q^{\text{*}}\right)$。

7. 结论

本文研究了具有工作休假和休假中断的M/M/1重试排队。顾客使用系统提供的信息来决定是进入系统还是止步。在不可见排队中过数值实例比较了均衡策略和社会最优策略，均衡策略下的社会收益和社会最优收益。均衡策略基本上大于社会最优策略，在不可见排队中均衡策略基本上大于社会最优策略，当服务员收取一定的费用时，可以促使顾客以社会最优策略进入系统。