带Group Lasso正则项的Pi-Sigma神经网络在线梯度算法研究

Online Gradient Algorithm for Pi-Sigma Neural Networks with Smooth Group Lasso Regularizer

摘要: Pi-Sigma神经网络是隐层带有求和神经元，输出层带有求积神经元的一种前馈神经网络，该网络具有较强的非线性映射能力。在误差函数中添加正则项是神经网络常用的优化方法，和传统的L2、L1/2正则项相比Group Lasso正则项可以在组级别上消除不必要的权值，具有良好的稀疏效果。众所周知，利用梯度法进行权值更新的学习方式有两种：一种是批处理学习算法，另一种是在线学习算法。本文提出带Group Lasso正则项的在线梯度学习算法来训练Pi-Sigma神经网络。最后，数值实验结果表明改进后的算法收敛速度更快并且具有较好的泛化性能。

Abstract: Pi-Sigma neural network is a feedforward neural network with summation neurons in hidden layer and quadrature neurons in output layer, which has strong nonlinear mapping ability. Adding regular terms to the error function is a common optimization method for neural networks. Compared with the traditional L2 and L1/2 regular terms, the Group Lasso regular terms can eliminate unnecessary weights at the group level and have a good sparse effect. As is known to all, there are two learning methods for weight update using gradient method: one is batch learning algorithm; the other is online learning algorithm. This paper proposes an online gradient learning algorithm with Group Lasso regularized terms to train Pi-Sigma neural networks. Finally, numerical results show that the improved algorithm converges faster and has better generalization performance.

1. 引言

人工神经网络已经被广泛应用于各种领域 [1]。其中前馈神经网络以其结构灵活性，具有与不同训练算法的兼容性的特点成为最受欢迎的体系结构之一。Pi-Sigma神经网络(简称PSNN)由Shin和Ghosh在1991年首先提出，它是前馈神经网络中的一种，具有良好的收敛性和泛化性能，该网络也具有较为规则的结构，并且具有更快的学习速度，能够通过增量添加单元来达到所需的复杂度水平 [2]，在分类实验和函数逼近实验中得到了良好的收敛性和准确性。该网络利用乘积神经元作为输出单元，在使用较少的权值和处理单元的同时，间接结合了高阶网络的能力，并且成功地应用到了许多领域 [3] [4] [5]。但该网络隐层中的求和神经元个数不易太多，否则会因为使用的权值太多而使该网络的学习速率降低，因此网络中隐层神经元的个数的多少很重要。合适大小的网络可以提高其泛化性能，因此寻找最合适的网络体系结构一直是一个重要的问题。正则化方法可以用来确定具有好的泛化性能的网络结构。

各种正则项已经被广泛应用，并且不同的正则项具有不同的作用，L₀正则项能够得到稀疏解，但它面临着NP难题且很难求解；对于L₁正则项来说，它的求解较为容易并且具有稀疏性；L₂正则项是很常用的一个正则项，它可以抑制权值过大的增长，但是没有稀疏性 [6]；L_1/2正则项具有稀疏性并且可以使网络具有好的泛化能力 [7]，但它只能删除接近于零的个体权值，而不能删除连接权值都接近于零的隐藏神经元；Group Lasso正则项可以在组水平上修剪不必要的权值和节点，使网络结构更稀疏 [8]。综上所述，L₂正则项不具有稀疏性，L_1/2正则项虽然具有稀疏性，但是稀疏效率不高，只能去掉个别稀疏的权值但并不能去掉整个的神经元节点，所以针对这一关键问题，在这里我们借用Group Lasso的思想在训练PSNN的过程中消除隐藏层的分组权重。Group Lasso正则项具有稀疏性，在网络结构的稀疏方面具有良好的效果，它的优势是具有组水平上的稀疏性，当保留必要的节点，同时将冗余的节点作为一个组进行惩罚时，修剪将更加直观和有效。

2. 相关研究

PSNN由于其良好的特性已经被许多学者研究，并且得到成功应用。熊焱 [9] 研究了PSNN的几种梯度学习算法，同时给出了相应算法学习能力和收敛性理论上的分析，并用仿真实验进行了验证；在喻昕等人 [10] 的论文中，为了克服权值过小导致的网络收敛速度慢的缺点，给出了基于乘子法随机单点在线梯度算法；聂勇等人 [11] 将混合遗传算法运用到PSNN中，并且证明了这种算法比遗传算法收敛更快；亢喜岱 [12] 给出了PSNN的随机输入在线梯度算法，对相应的收敛性进行了证明。在这篇文章中，我们给出带Group Lasso正则项的PSNN的在线梯度学习算法，来进一步优化网络结构。

3. Pi-Sigma神经网络算法描述

令PSNN输入层的神经元个数为n，隐层(求和层)的神经元个数为D，输出层(求积层)的神经元个数1，记连接输入层和求和层第l个神经元的权值向量为 $w_l={\left(w_{l1},\cdots ,w_{\mathrm{l}n}\right)}^{\text{T}}\in R^n\left(1\le l\le D\right)$，并记 $w={\left(w_1^{\text{T}},\cdots ,w_D^{\text{T}}\right)}^{\text{T}}\in R^{nD}$。对于连接求和层和输出层的权值都为1。有一个输入为 $x_n=-1$，对应的偏置为 $w_{Dn}$。激活函数为 $g:R\to R$。结构图如图1所示。

Figure 1. Structure diagram of Pi-Sigma neural network

图1. Pi-Sigma神经网络结构图

通过给定一个输入向量 $x\in R^n$，网络的实际输出为

$y=g\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(w_{li}{x}_i\right)}\right)}\right)=g\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x\right)}\right)$ (1)

其中 $w_l\cdot x$ 代表着 $w_l$ 和x的内积。

3.1. 带L₂正则项的在线梯度算法

将训练样本 ${\left\{x^m,O^m\right\}}_{m=1}^M\subset R^n\times R$ 输入给网络，其中 $O^m$ 是输入向量 $x^m$ 的理想输出。将L₂正则项加入误差函数中，最终的误差函数形式为：

$\begin{array}{c}E\left(w\right)=\frac{1}{2}{\displaystyle \underset{m=1}{\overset{M}{\sum }}{\left(O^m-g\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right)\right)}^2}+\lambda {\displaystyle \underset{l=1}{\overset{D}{\sum }}{\Vert w_l\Vert }^2}\\ ={\displaystyle \underset{m=1}{\overset{M}{\sum }}{g}_m}\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right)+\lambda {\displaystyle \underset{l=1}{\overset{D}{\sum }}{\Vert w_l\Vert }^2}\end{array}$ (2)

其中， $\lambda$ 是正则项的参数， $g_m\left(t\right)=\frac{1}{2}{\left(O^m-g\left(t\right)\right)}^2$。

因此可以得到(2)式关于 $w_k$ 的偏导：

$E_{w_k}\left(w\right)={\displaystyle \underset{m=1}{\overset{M}{\sum }}{g^{\prime }}_m}\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right){\displaystyle \underset{\begin{array}{l}l=1\\ l\ne k\end{array}}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)x^m}+2\lambda w_k$ (3)

其中 $l=1,2,\cdots ,D$。

给定一个随机初始权值 $w_0$，在线学习算法的权值更新公式为：

$w^{iM+m}=w^{iM+m-1}-{\eta }_i{\Delta }_m^i{w}^{iM+m-1}$ (4)

其中 $i=0,1,2,\cdots ;m=1,2,\cdots ,M$。

${\Delta }_m^i{w}_k^{iM+m-1}={g^{\prime }}_m\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l^{iM+m-1}\cdot x^m\right)}\right){\displaystyle \underset{\begin{array}{l}l=1\\ l\ne k\end{array}}{\overset{D}{\prod }}\left(w_l^{iM+m-1}\cdot x^m\right)x^m}+\frac{2\lambda }{M}{w}_k^{iM+m-1}$ (5)

3.2. 带L_1/2正则项的在线梯度算法

将一组训练样本 ${\left\{x^m,O^m\right\}}_{m=1}^M\subset R^n\times R$ 输入到网络，其中 $O^m$ 是输入向量 $x^m$ 的理想输出。将L_1/2正则项加入误差函数中，误差函数最终的形式为：

$\begin{array}{c}E\left(w\right)=\frac{1}{2}{\displaystyle \underset{m=1}{\overset{M}{\sum }}{\left(O^m-g\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right)\right)}^2}+\lambda {{\displaystyle \underset{l=1}{\overset{D}{\sum }}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|w_{li}\right|}}}^{\frac{1}{2}}\\ ={\displaystyle \underset{m=1}{\overset{M}{\sum }}{g}_m}\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right)+\lambda {{\displaystyle \underset{l=1}{\overset{D}{\sum }}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|w_{li}\right|}}}^{\frac{1}{2}}\end{array}$ (6)

其中， $\lambda$ 是正则项的系数， $g_m\left(t\right)=\frac{1}{2}{\left(O^m-g\left(t\right)\right)}^2$。

因此可以得到(6)式关于 $w_{ki}$ 的偏导：

$E_{w_{ki}}\left(w\right)={\displaystyle \underset{m=1}{\overset{M}{\sum }}{g^{\prime }}_m}\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right){\displaystyle \underset{\begin{array}{l}l=1\\ l\ne k\end{array}}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)x_i^m}+\frac{\lambda \mathrm{sgn}\left(w_{ki}\right)}{2{\left|w_{ki}\right|}^{\frac{1}{2}}}$ (7)

其中 $l=1,2,\cdots ,D$。

给定一个随机初始权值 $w_0$，在线学习算法的更新公式为：

$w^{iM+m}=w^{iM+m-1}-{\eta }_i{\Delta }_m^i{w}^{iM+m-1}$ (8)

其中 $i=0,1,2,\cdots ;m=1,2,\cdots ,M$。

${\Delta }_m^i{w}_{ki}^{iM+m-1}={g^{\prime }}_m\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l^{iM+m-1}\cdot x^m\right)}\right){\displaystyle \underset{\begin{array}{l}l=1\\ l\ne k\end{array}}{\overset{D}{\prod }}\left(w_l^{iM+m-1}\cdot x^m\right)x_i^m}+\frac{\lambda \mathrm{sgn}\left(w_{ki}^{iM+m-1}\right)}{2M{\left|w_{ki}^{iM+m-1}\right|}^{\frac{1}{2}}}$ (9)

3.3. 带Group Lasso正则项的在线梯度算法

将一组训练样本 ${\left\{x^m,O^m\right\}}_{m=1}^M\subset R^n\times R$ 输入到网络，其中 $O^m$ 是输入向量 $x^m$ 的理想输出。将Group Lasso正则项加入误差函数中，误差函数最终的形式为：

$\begin{array}{c}E\left(w\right)=\frac{1}{2}{\displaystyle \underset{m=1}{\overset{M}{\sum }}{\left(O^m-g\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right)\right)}^2}+\lambda {\displaystyle \underset{l=1}{\overset{D}{\sum }}\Vert w_l\Vert }\\ ={\displaystyle \underset{m=1}{\overset{M}{\sum }}{g}_m}\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right)+\lambda {\displaystyle \underset{l=1}{\overset{D}{\sum }}\Vert w_l\Vert }\end{array}$ (10)

其中， $\lambda$ 是正则项的系数， $g_m\left(t\right)=\frac{1}{2}{\left(O^m-g\left(t\right)\right)}^2$。

因此可以得到(10)式关于 $w_k$ 的偏导：

$E_{w_k}\left(w\right)={\displaystyle \underset{m=1}{\overset{M}{\sum }}{g^{\prime }}_m}\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)}\right){\displaystyle \underset{\begin{array}{l}l=1\\ l\ne k\end{array}}{\overset{D}{\prod }}\left(w_l\cdot x^m\right)x^m}+\lambda \frac{w_k}{\Vert w_k\Vert }$ (11)

其中 $l=1,2,\cdots ,D$。

给定一个随机初始权值 $w_0$，在线学习算法的更新公式为：

$w^{iM+m}=w^{iM+m-1}-{\eta }_i{\Delta }_m^i{w}^{iM+m-1}$ (12)

其中 $i=0,1,2,\cdots ;m=1,2,\cdots ,M$。

${\Delta }_m^i{w}_k^{iM+m-1}={g^{\prime }}_m\left({\displaystyle \underset{l=1}{\overset{D}{\prod }}\left(w_l^{iM+m-1}\cdot x^m\right)}\right){\displaystyle \underset{\begin{array}{l}l=1\\ l\ne k\end{array}}{\overset{D}{\prod }}\left(w_l^{iM+m-1}\cdot x^m\right)x^m}+\frac{\lambda w_k^{iM+m-1}}{M\Vert w_k^{iM+m-1}\Vert }$ (13)

4. 数值模拟

为了验证该算法的有效性，这里使用一个函数逼近实验为例，利用带L₂正则项，L_1/2正则项，Group

Lasso正则项的算法来逼近函数： $G\left(x\right)=x\cdot coc\left(\frac{\pi }{2}x\right)$。输入样本维数为3，输入样本个数为101个，3个

隐层神经元，1个输出，在这里惩罚项系数 $\lambda =0.0001$，学习率为 $\eta =0.0004$，最大迭代步数为5000，误差标准为10⁻⁴。图2，图3和图4分别为带L₂正则项，带L_1/2正则项以及带Group Lasso正则项的算法逼近函数 $G\left(x\right)$ 的图像，在这三幅图中，实线为函数 $G\left(x\right)$ 函数图，另一条为相应的逼近图。图5和图6分别给出了这三种算法的误差函数图和梯度范数图。

在这三种算法的逼近图中，实线为要逼近的函数的曲线，另一条为相应算法逼近该函数的曲线，两条曲线的重合度越高，则说明相应的算法的逼近效果越好。从图2，图3和图4中我们可以看到，在相同的参数条件下，带Group Lasso正则项的算法逼近 $G\left(x\right)$ 的曲线与 $G\left(x\right)$ 本身的曲线重合度最高，因此说明提出的新算法比带L₂正则项和带L_1/2正则项的算法的逼近效果都好，同时也说明了新算法具有更好的泛化性能。三种算法的误差函数和梯度范数是单调递减并且收敛的，收敛前越靠近y轴，说明收敛的速度越快，收敛后越接近x轴说明误差或梯度范数越小，从图5和图6中可以看到，带这三种正则项的算法的误差函数和梯度范数单调都是单调递减趋于0的，同时可以看出带Group Lasso正则项的算法收敛速度最快，误差最小。

Figure 2. Algorithm approximation diagram with L₂ regular term

图2. 带L₂正则项的算法逼近图

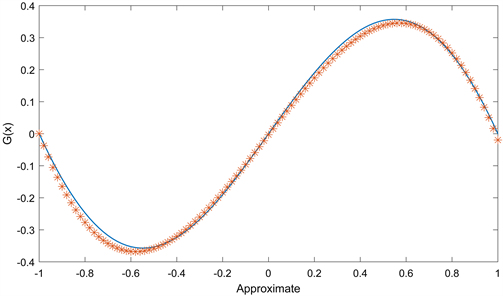
Figure 3. Algorithm approximation diagram with L_1/2 regular term

图3. 带L_1/2正则项的算法逼近图

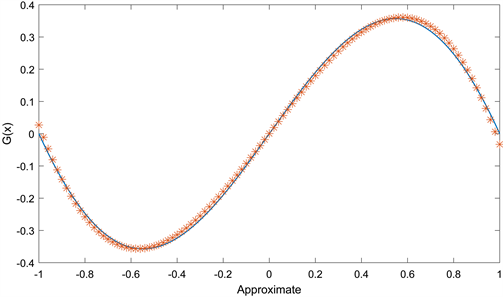
Figure 4. Algorithm approximation diagram with Group Lasso regular term

图4. 带Group Lasso正则项的算法逼近图

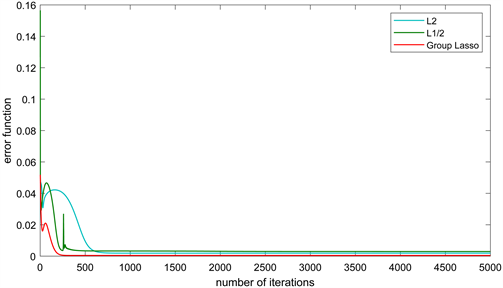
Figure 5. Error function diagram of three algorithms

图5. 三种算法的误差函数图

Figure 6. Norm of gradient graph of three algorithms

图6. 三种算法的梯度范数图

5. 结束语

本文中，我们考虑了Group Lasso惩罚项的良好稀疏性能，提出了带Group Lasso正则项的Pi-Sigma神经网络的在线梯度学习算法。通过函数逼近实验，根据三种算法的逼近效果图，误差函数图以及梯度范数图验证了该算法的有效性。