基于EIN覆盖网的复杂网络最短路径近似算法

The Approximate Shortest Path Algorithm for Complex Networks Based on EIN Overlay Network

摘要: 在网络规模远超出最短路径经典算法适用范围的情况下，最短路径近似算法成为有效的替代解决方案。针对现有近似算法存在的预处理阶段计算效率低、算法性能受网络规模影响较大等问题，提出一种基于EIN覆盖网络的大规模复杂网络最短路径近似算法。算法基于边递归网络(The network created by edge iterations, EIN)的生成和标号方式在实际复杂网络上抽象出具有确定性拓扑结构的标号覆盖网络，结合覆盖网络标号节点间确定的位置信息快速推导出实际复杂网络中最短路径的近似解，在确定性网络层面高效解决非确定性复杂网络的最短路径问题。真实网络数据集上的实验结果表明，所提方法在大规模复杂网络上能保证较高精确度的同时，大幅度降低计算成本。

Abstract: The shortest path approximation algorithm becomes an effective alternative solution when the network scale is far beyond the scope of the classical shortest path algorithm. Aiming at the problems existing in the existing approximation algorithms, such as low computational efficiency in the preprocessing stage, and the algorithm performance that is greatly affected by the network scale, a shortest path approximation algorithm for large-scale complex networks based on EIN overlay network is proposed. The algorithm abstracts the label overlay network with deterministic topology structure on the actual complex network based on the generation and labeling method of EIN (The network created by edge iterations), and quickly deduces it by combining the location information determined between the label nodes of the overlay network. The approximate solution of the shortest path in the actual complex network can efficiently solve the shortest path problem of the non-deterministic complex network at the deterministic network level. The experimental results on real network datasets show that the proposed method can greatly reduce the computational cost while ensuring high accuracy on large-scale complex networks.

1. 引言

信息时代已成为人类社会发展的必然趋势，科学信息化、社会信息化带动着世界性的巨大变革。在大数据时代的背景下，复杂网络自然而然地成为了一门深刻的研究课题。复杂网络是现实世界中各种实体之间关系的高度抽象，包括社交网络、交通系统、电网和病毒传播。因此，关于复杂网络的理论研究涵盖了实际生活中的众多领域，具有巨大的应用价值。

在复杂网络中寻找任意两个节点之间的最短路径 [1] 一直是众多专家研究和讨论的一个重要问题。现有的最短路径精确算法，例如Dijkstra [2] 和Floyd [3]，是通过大量的计算来求得节点间的精确距离，这很适用于早期的小型网络。但随着数据规模的迅猛增长，精确算法效率低的缺点被不断放大。对于大规模网络和实时网络，学者们更关注于算法的计算效率。在误差可接受的范围内，高效计算出良好的近似路径来替代精确路径已被证实为可行的替代解决方案。最短路径近似算法的常用设计方法包括启发策略 [4] [5]、分层策略 [6] [7]、地标点策略 [8] [9] 等，都是通过预处理保留网络部分重要信息，达到提高计算效率的目的。文献 [10] 提出了基于区域中心点距离(centers distance of zone, CDZ)的最短路径近似算法，该算法结合了中心性度量方法筛选出中心节点集合，基于区域中心点间的精确路径去估算全局节点对间的最短路径。CDZ算法的准确性在大规模网络上表现突出，但其预处理阶段花费的时间较长，算法的时间效率受网络规模的影响较大。文献 [11] 中提出的基于k-shell的最短路径(K-shell shortest path approximation algorithm, KS)近似算法将网络划分为不同层次的k-shell子图，利用高层网络间的精确路径引导路径搜索。虽然KS算法相比于CDZ算法降低了中心节点的规模，但仍旧依赖于区域节点间的精确计算，导致计算效率偏低。Dennis [12] 提出超点聚合的分层方法来降低网络的规模，通过压缩搜索空间来提高计算效率。但算法在聚合中心节点的过程中需要构建多层网络，消耗了过多的存储空间。

尽管近年来围绕着大规模复杂网络的最短路径近似算法方面的研究已经取得了一些突破和成果，但是，总体上该研究仍然处于发展中阶段。现有的最短路径近似算法大都或多或少的存在一些缺陷与不足，在搜索效率、计算精度以及存储消耗方面通常各有利弊，很多算法效率的提高都是以牺牲大量的预处理或搜索精度为代价的，因而如何在保障精确度的情况下不消耗过多的预处理时间及存储空间来找到近似路径，尚有待于进一步研究。复杂网络拓扑的随机性是加重最短路径计算成本的主要原因之一，目前针对复杂网络随机性展开的研究寥寥无几。而确定性复杂网络 [13] 相较于随机网络的优势在于能依据确定的拓扑关系推断出复杂网络结构性质的解析解。鉴于此，本文结合覆盖网络和确定性网络的概念，提出基于EIN [14] 覆盖网络(EIN overlay network，简称EON)的最短路径近似算法，EON算法基于边递归网络模型EIN的生成方式与拓扑特性构建确定性覆盖网络并对节点进行标号，将随机网络任意两点间的最短路径问题抽象到确定性网络的层面处理，利用节点标号性质更加准确高效地搜索大规模复杂网络节点之间的最短路径。

2. 基本概念

2.1. 基于标号的确定性路由算法

确定性网络作为研究人员设计出来分析计算复杂网络的工具，结构和特征都接近于实际中的网络。相比于随机网络，确定性网络的优势在于能通过严格的推导求出特定解。文献 [15] 提出了一种用于Farey族顶点的标号方法，并基于标号推导出Farey族网络任意节点间的最短路径。

Farey网由著名的Farey序列 [16] [17] [18] 推导而来。假设Farey图为 $F\left(t\right)$，其中是t迭代的步数， $F\left(t\right)$ 通过以下两个步骤迭代生成：

1) 当 $t=0$ 时， $F\left(0\right)$ 由两个初始节点和一条活动边组成。

2) 当 $t\ge 0$ 时， $F\left(t\right)$ 由 $F\left(t-1\right)$ 得到，方法是在所有 $t-1$ 时刻加入的活动边上增加一个新节点，并将新节点与边两端的节点相连。

边递归网络EIN是Farey网的衍生，它由三个Farey网络而组成，记为 $N\left(t\right)$。其生成方式为以下两步：

1) 当 $t=0$ 时， $N\left(0\right)$ 由三个初始节点和三条活动边组成。

2) 当 $t\ge 0$ 时，在 $N\left(t-1\right)$ 中所有 $t-1$ 时刻加入的活动边上增加一个新节点并连接至边的两端，得到 $N\left(t\right)$。

结合确定性网络的生成方式对节点进行标号，是推导最短路径的关键，标号能反映出节点间的拓扑关系。Farey网和EIN网的生成和标号过程分别如图1和图2所示。

Figure 1. The labeling of $F\left(t\right)$ for $t=0,1$ and 2

图1. $t=0,1$ 和2时刻递归生成的标号 $F(\; t\; )$

Figure 2. The labeling of $N\left(t\right)$ for $t=0,1$ and 2

图2. $t=0,1$ 和2时刻递归生成的标号 $N(\; t\; )$

Farey网和EIN网络具有以下标号性质：

性质1：Farey网和EIN网中的任意节点能根据标号推导出所有相邻节点标号。

性质2：对于 $t\ge 1$ 的 $F\left(t\right)$，可视为由两个子网 $F_1\left(t-1\right)$ 和 $F_2\left(t-1\right)$ 组成。不同子网节点对间最短路径经过的中间节点，可由节点对所处区域(根据标号来判断)间的关系推导出。

性质3：对于Farey网中的每个节点对，存在一个最小公共子网(MCSG)包含其所有最短路径。

基于以上标号性质，可以线性时间复杂度找出Farey网和EIN网中任意标号节点对间的所有最短路径。

算法1：(SPAF) Farey网的最短路径算法主要分为三步。首先，通过性质3确定目标节点对的最小公共子网MCSG。其次，根据性质2找出最短路径经过的中间节点。最后，目标节点与中间节点组成新的节点对继续重复整个流程，直到根据性质1判断出所有新的节点对都互为邻居为止，得出目标节点对之间的所有最短路径。

算法2：(SPAN)将 $N\left(t\right)$ 看作由三个Farey子网 $F_0\left(t\right)$ 、 $F_0\left(t\right)$ 和 $F_2\left(t\right)$ 组成。当目标节点对位于相同子网时，求最短路径的过程与上述SPAF算法相同。当目标节点对位于不同子网时，两个子网可构成一个完整的 $F\left(t+1\right)$，输入标号改变后可由SPAF算法求出最短路径。

SPAF算法和SPAN算法都能在线性时间 $O\left(n\right)$ 内确定任意节点对间最短路径的所有可能，求出所有节点对的最短路径也仅用次平方的时间复杂度。

2.2. 覆盖网络

覆盖网络是面向应用层的顶层网络，常为特定应用提供专用的虚拟网络拓扑。覆盖网络中的边是底层网络中物理路径的抽象，节点针对需求以多种方式逻辑互连。这种灵活性让覆盖网络成为了互联网中特定问题的有效解决方案，文献 [19] 提出了一种覆盖网络对IP层路径异常进行快速检测和恢复，以此提高用户体验。本文EON算法结合覆盖网络思路，构建虚拟EIN网络拓扑，实现大规模复杂网络近似路径的高效搜索。

3. 基于EIN的最短路径近似算法EON

EON算法的思路是将实际非确定性复杂网络任意两点间的最短路径问题带到确定性网络的层面上来解决。需要结合覆盖网络技术，基于边递归网络EIN的生成和标号方式在实际复杂网络上抽象出服务于高效最短路径近似搜索的EIN覆盖网络。

3.1. EIN覆盖网络构建

节点集V和边集E组成的无向无权网络记为 $G=\left(V,E\right)$，EON算法构建出来的覆盖网络则表示为 $G_o\left(t\right)=\left(O,E_o\right)$。其中覆盖网的节点集合 $O=\left(O_1,O_2\right)$ 由两类节点组成， $O_1$ 表示EIN覆盖网中的标号节点集合， $O_2$ 则表示EIN覆盖网中标号节点的邻居节点集合。覆盖网标号节点依据EIN网的生成方式进行覆盖，将t时刻的活动边记为 $E_a\left(t\right)$。EON算法构建EIN覆盖网络基于以下步骤：

1) 选择EIN覆盖网络的三个初始节点。

从EIN网的生成过程来看，图的所有顶点在每一步迭代中将它们的度数增加两个单位，越早加入的节点度数越高。因此本文对底层网络节点 $v\in V$ 进行度值排序，依照度值逆序在前1%的节点中找到能形成三角结构且度值之和最大的三个节点作为初始标号节点0，1，2。

2) 基于EIN网络的生成方式进行覆盖网络扩展。

标号节点间的路径是EON算法进行最短路径近似搜索的依据。大部分实际复杂网络具有无标度特性，其度分布均符合或接近幂律分布 [10]。当标号节点度数之和超过全图的50%时，标号节点直接涉及全图大部分的边。因此，EON算法基于以下步骤进行覆盖网络的构建：

Step 1：将初始节点0，1，2加入集合 $O_1$，此时 $t=0$， $E_a\left(0\right)=E_o\left(0\right)=\left\{\left(0,1\right),\left(0,2\right),\left(1,2\right)\right\}$。

Step 2：依次找到 $E_a\left(t\right)$ 中每条活动边两端节点s和t的度值最高的共同邻居 $v_n$ 加入 $O_1\left(t+1\right)$，其组成的边 $\left(s,v_n\right)$ 和 $\left(v_n,t\right)$ 则加入 $E_a\left(t+1\right)$ 中。

Step 3：判断 $E_a\left(t+1\right)$ 是否为空，是则表示无符合生成方式的节点进行扩展，依次找到 $G_o$ 最外层中每条边的两端节点s和t的度值最高的邻居 $v_n$ 加入 $O_1\left(t+1\right)$，其组成的边 $\left(s,v_n\right)$ 和 $\left(v_n,t\right)$ 则加入 $E_a\left(t+1\right)$ 中，此时边 $\left(s,v_n\right)$ 和 $\left(v_n,t\right)$ 与底层网络对应边的映射关系如图3所示， $\left(s,v_n\right)$ 在覆盖网络的权重为2。

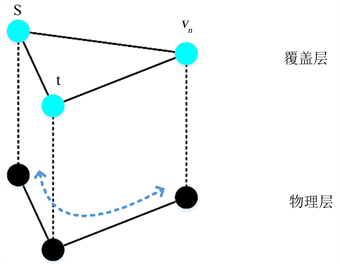
Figure 3. Mapping of conflicting nodes

图3. 冲突节点的映射方式

Step 4：如果集合 $O_1$ 中节点的度数之和大于全图度数之和的50%，则转到第五步；反之，使 $t=t+1$， $E_o\left(t\right)=E_a\left(t\right)$，继续执行第二步。

Step 5： $O_1$ 节点间在实际网络中的路径映射到覆盖网络中，覆盖网络 $G_o$ 初步构造完成，将 $V-O_1$ 的节点加入集合 $O_2$。

3) 基于EIN网络的标号方式对覆盖网络的节点进行标号。

节点标号格式为 $a.b.c$，其中 $a\in \left\{0,1,2\right\}$ 表示节点所属的Farey子网 $F_a\left(t\right)$， $b\in \left\{1,2,\cdots ,t\right\}$ 和 $c\in \left\{1,2,\cdots ,2^{b-1}\right\}$ 则表示节点在子网 $F_a\left(t\right)$ 中的位置。

4) 建立标号节点与其余节点的联系。

通过广度优先遍历依次找到最接近标号节点 $s\in O_1$ 的邻居 $t\in O_2$，将其在实际网络中的路径抽象到覆盖网络上的边 $\left(s_o,t_o\right)$。

图4为构建EIN覆盖网的一个简单示例。图4(a)~(d)展示了基于边递归网络EIN的生成方式进行覆盖网络初步覆盖的过程，t时刻的活动边用红色标注。图4(e)和图4(f)表示GEIN覆盖网的标号过程。完整的EIN覆盖网如图4(g)所示。

3.2. 最短路径近似搜索

在实际复杂网络上抽象出EIN覆盖网络后，标号节点间的位置信息能通过标号快速推导出来。EON算法利用标号节点的位置信息，在目标节点对进行最短路径近似搜索的过程中，利用EIN覆盖网络标号节点对间的距离判断节点出现在最短路径的可能性，排除低概率的节点方向来限制搜索范围，从而提高路径搜索的效率。EON算法的最短路径近似搜索过程如下：

Figure 4. Construction process of EIN overlay network

图4. EIN覆盖网的构建过程

1) 计算EIN覆盖网络标号节点间的最短路径距离。

记 $d_E\left(l_s,l_t\right)$ 为标号节点 $s,t$ 在EIN网络拓扑上的最短路径距离，其中 $l_s,l_t$ 为节点标号。 $d_E$ 作为EON算法对路径近似估算的判断，可用SPAN算法高效得出。在算法SPAN中，求得全节点对间最短路径(The all-pairs shortest paths problem, APSP)需要次平方的运算时间 $O\left(n^{2-\delta }\right)$，其中 $\delta >0$。由于边递归网络EIN是递归构成的，外层节点对间的最短路径包含内层节点对的最短路径。因此由内向外去计算标号节点对间的最短路径距离，能提高SPAN算法的计算效率。

2) 基于 $d_E$ 值迭代搜索最短近似路径

节点在搜索去往目标节点最短路径的过程中，选取 $d_E$ 值与边权重之和最低的邻居加入最短近似路径序列，并将其作为新的起始节点，直到与目标节点直接相连。

实际网络中任意节点间的距离 $d\left(s,t\right)$ 可以表示为：

$d\left(s,t\right)=\{\begin{array}{ll}{d}_O\left(l_s,l_t\right)\hfill & s,t\in O_1\hfill \\ d\left(s,n_{s_o}\right)+d_O\left(l_{n_{s_o}},l_t\right)\hfill & s\in O_2,t\in O_1\hfill \\ d\left(s,n_{s_o}\right)+d_O\left(l_{n_{s_o}},l_{n_{t_o}}\right)+d\left(t,n_{t_o}\right)\hfill & s,t\in O_2,l_s\ne l_t\hfill \\ d\left(s,LC{A}_{st}\right)+d\left(t,LC{A}_{st}\right)\hfill & s,t\in O_2,l_s=l_t\hfill \end{array}$ (1)

如果目标节点都属于标号节点集合 $O_{\text{1}}$，节点间的距离为其在EIN覆盖网络上的最短近似路径长度 $d_O$。

如果目标节点对中存在 $O_{\text{2}}$ 集合中的节点，节点间的距离除了包括标号节点对间的最短近似路径长度，还需要考虑节点 $S\in O_{\text{2}}$ 和其覆盖网络邻居 $n_{S_O}$ 在实际网络上的映射路径长度。

如果目标节点都属于 $O_{\text{2}}$ 集合，且它们在覆盖网络上具有相同的标号邻居。通过节点对到标号节点的最短路径序列可以快速找到它们的最近公共祖先。目标节点间的距离为其通往最近公共祖先的路径长度之和。

图5为EON算法的一个简单示例。节点9到节点7的最短近似路径搜索过程中，核心在于选取节点5之后最有可能存在最短路径上的节点。此时节点5的邻居标号分别为1、2和2.1.1，通过SPAN算法可推导出节点1，3，4在EIN网络拓扑上到节点7的最短路径集合分别为{{1，2.1.1，2.2.1}，{1，0，2.2.1}}、{{2，0，2.2.1}}和{{2.1.1，2.2.1}}，由此可推断节点4为最可能出现在最短路径上的节点。最终得到节点9到节点7的最短近似路径{9，8，5，4，7}。

Figure 5. Example diagram of EON

图5. EON算法示例图

4. 实验与分析

4.1. 数据集及评估指标

EON算法在PyCharm集成开发环境上使用Python语言实现，运行环境处理器为Intel Corei5-8265U @1.80 GHz，内存为8 GB。选用四个不同规模和类型的无向无权真实网络评估本文算法，分别是ego-Facebook [20]、email-Enron [21]、com-DBLP [22] 和soc-BC。ego-Facebook数据的采集来自Facebook应用程序调查的参与者，节点代表参与者的账号，边则代表两个账号之间的好友关系。email-Enron涵盖了上万封Enron公司管理的电子邮件通信记录，数据集最初由联邦能源监管委员会在调查期间公开并发布到网络上。soc-BC为博客目录网络，包含了用户之间的所有链接。com-DBLP来源于计算机科学杂志，网络代表同期刊或会议等出版地点的作者形成的真实社区。如表1所示，通过4个指标来展示实验网络的基本信息，分别是节点数量V、边的数量E、平均聚类系数ACC和网络直径D。

Table 1. Basic information on the five networks

表1. 实验网络的基本信息

本文选择平均路径比p [23] 作为最短路径近似算法准确性的度量指标。p的定义如下：

$p=\frac{{\displaystyle \underset{i=1}{\overset{p_r}{\sum }}{p}_{A_i}}}{{\displaystyle \underset{i=1}{\overset{p_r}{\sum }}{p}_{D_i}}}$ (2)

其中 $p_r$ 是节点对的数量， $p_{A_i}$ 代表由近似算法求出的第i对节点间的近似距离， $p_{D_i}$ 代表由Dijkstra算法求出的第i对节点间的精确距离。近似算法的精确度取决于p接近1的程度。

最短路径近似算法的计算效率由预处理时间 $T_{init}$ 和平均查找时间 $T_S$ 来反映。实验通过在测试网络上随机得到10,000个节点对，取其平均运行时间作为算法的 $T_S$。

4.2. 实验结果与分析

表2展示了EON算法、KS算法和CDZ算法在4个目标网络的准确性实验结果。三种算法在4个实验网络中的平均路径比p都低于1.1，说明EON算法、KS算法和CDZ算法计算出的近似路径仅与精确路径存在不到10%的误差，都具有较高的准确率。KS算法和CDZ算法利用不同的中心性指标去评估节点的重要性，选取一定规模的重要节点作为中心节点，通过中心节点间的精确路径来保证算法的准确性。EON算法则是利用实际网络中的确定性拓扑结构的位置信息来保证算法的准确性。

Table 2. Accuracy of approximation algorithms in different networks

表2. 近似算法在不同网络上的准确性

从表3中可以发现，EON算法在计算效率上相较于其他两种近似算法有明显的优势。KS算法和CDZ算法在预处理时间 $T_{init}$ 和平均查找时间 $T_S$ 这两个数据方面远劣于本文算法，特别是在大规模网络com-DBLP的实验中，时间开销是EON算法的上百倍。

Table 3. Computational efficiency of approximation algorithms in different networks

表3. 近似算法在不同网络上的计算效率

CDZ算法和KS算法在最短路径近似搜索的过程中依赖于中心/高层节点间的精确路径，需要在预处理阶段花费 $O\left(d^3\right)$ 的时间，其中d为中心/高层节点的数量。虽然中心/高层节点在全图的占比(约占节点总数5%~10%)并不高，但放大到大规模实际网络中，这任是一笔不可忽视的巨大开销。EON算法的近似搜索则依赖于标号节点间在EIN拓扑结构上的精确路径，结合包含节点间拓扑关系的标号信息，仅需 $O\left(t^{2-\delta }\right)$ 的时间复杂度可推导出，其中t为覆盖网络标号节点的数量。

EON算法基于边递归网络EIN的生成方式构建覆盖网络，标号节点间的拓扑结构是固定的，因此提前计算并存储一定规模EIN网络标号节点间的最短路径，不同实际网络的近似路径搜索情况下，能节省大量的重复计算时间。复杂的网络系统是呈现动态的 [24]，这种动态由多种变化过程产生，例如进化、学习和衰老。巨大的预处理开销在需要频繁的对网络进行重复计算或者只计算部分重要节点对的最短路径的情况下显然是不能被接受的。相比于现有的最短路径近似算法，EON算法能快速适应网络变化，更具灵活性。

EON算法和CDZ算法在email-Enron网络和soc-BC网络不同规模子网络上的性能变化如表4和表5所示。相比于CDZ算法，EON算法具有明显的性能优势，特别是在平均计算时间数据方面的表现上。5000到30,000节点规模的跨度中，CDZ算法的平均计算时间横跨了三个计数单位，本文算法在保证高准确度的同时，能维持平均计算时间的增长在一个计数单位内。证明EON算法适应网络规模增长代价低，更加适用于节点规模大的实际复杂网络。

Table 4. Performance of approximation algorithms in different scale email-Enron networks

表4. 近似算法在不同规模email-Enron网络上的表现

Table 5. Performance of approximation algorithms in different scale soc-BC networks

表5. 近似算法在不同规模soc-BC网络上的表现

5. 总结

本文针对复杂网络最短路径近似算法预处理阶段时间或空间成本过高、计算效率受网络规模影响较大的问题，利用确定性网络能够基于节点间确定的位置关系快速推导出最短路径解析解这一特点，提出基于EIN覆盖网络最短路径近似算法EON。经过在社交网络、引文网络、博客目录网络等实际复杂网络的一系列实验结果表明，EON算法在不同规模的无向无权网络中能保证高准确度和计算效率的同时，以较低的代价适应网络规模的增长，更适用于大规模实际复杂网络。

从确定性模型的层面去解决随机场景下的网络节点间最短路径问题是近似算法的一种新的解决思路。深入研究不同类型的实际复杂网络与确定性网络拓扑之间的联系，评估与改进覆盖网络的构建方法，是我们未来研究工作的重点。