基于椭球积分的集群扰动及其数值方法

Cluster Disturbance Based on Ellipsoid Calculus and Its Numerical Method

摘要: 本文基于椭球积分考察了具有随机扰动的集群控制问题。通过HJB方程计算值函数，并建立数值方法得到集群的最优控制。主要结论可用于处理集群在风场、信号场等现实场景的运动控制问题。

Abstract: In this paper, the cluster control problem with random disturbance is investigated based on the ellipsoid integral. The value function is calculated by the HJB equation, and a numerical method is established to obtain the optimal control of the swarm. The main conclusions can be used to deal with the movement of the cluster in real scenes such as wind field and signal field.

1. 引言

本文考察具有非退化椭球值轨迹的多值控制微分系统。无论是Pontryagin LS处理基于控制参数满足限制条件的最优控制问题 [1]，还是Bellman R和Kalaba R等学者依据Lyapunov技术、Bellman动态规划和Pontryagin极大值原理的优化技术进行分析和综合 [2]，或者是Krasovskii NN提出的关于线性系统的运动控制理论 [3]，这些理论方法都是解决最优控制问题的相关工具，对集值微积分和集值动力学的发展具有重要意义 [4]。

俄罗斯莫斯科国立大学的Kurzhanski AB教授团队一直致力于对控制问题的各方面研究，尤其在根据椭球逼近方法考察集群运动问题上颇有成果。早在1991年该团队就考察了椭球技术在动力学系统建模中各种问题中的应用 [5]。以Krasovski NN的极值瞄准策略概念为基础 [6]，研究了集值映射的椭圆值演算的构造解及其相关逼近技术。产生了适用于算法过程和计算机图形模拟的建设性方案 [7]。进一步在控制综合问题中引入有界扰动，Kurzhanski AB团队同样采用动态系统的椭球技术来处理此类不确定系统的问题 [8]。

本文共分为五节，第一节介绍基本椭球系统；第二节介绍具有随机扰动的椭球系统，并给出最优控制的求解过程；第三节通过数值仿真给出椭球运动的轨迹管；第四节分析了算法的合理性；第五节是对全文的总结和展望。

2. 基本椭球系统

首先介绍椭球控制中的基本概念符号，包括非退化椭球的定义、椭球中心、构型矩阵、目标函数等内容。

定义1.1 [9] 定义 ${ℝ}^n$ 空间中以q为中心、以Q为构型矩阵的非退化椭球如下

$\epsilon \left(q,Q\right)=\left\{x\in {ℝ}^n:\langle x-q,Q^{-1}\left(x-q\right)\rangle \le 1\right\},$

其中 $q\in {ℝ}^n$， $Q\in {ℝ}^{n\times n}$， $Q=Q^{\prime }>0$， $Q^{\prime }$ 表示矩阵Q的转置， $\langle \cdot ,\cdot \rangle$ 表示内积， $\langle x,Qx\rangle >0$ 对所有 $x\in {ℝ}^n$ 均成立。

考察定义在时间区间 $\left[t_0,\theta \right]$ 上的线性时变系统，其运动方程为

$\stackrel{\dot{}}{q}\left(t\right)=A\left(t\right)q+C\left(t\right)u\left(t\right),q\left(t_0\right)=q^0,$ (1)

$\stackrel{\dot{}}{Q}\left(t\right)=T\left(t\right)Q+Q^{\prime }T\left(t\right)+B\left(t\right)U\left(t\right)B^{\prime }\left(t\right),Q\left(t_0\right)=Q^0,$ (2)

矩阵函数 $A\left(t\right)\in {ℝ}^{n\times n}$， $B\left(t\right)\in {ℝ}^{n\times m_2}$， $C\left(t\right)\in {ℝ}^{n\times m_1}$， $T\left(t\right)\in {ℝ}^{n\times n}$ 均关于时间t连续，其中 $u\left(t\right)\in {ℝ}^{m_1}$ 是对中心q的控制， $U\left(t\right)\in {ℝ}^{m_2\times m_2}$ 是对构型矩阵Q的控制，且 $T\left(t\right)$ 、 $U\left(t\right)$ 为对称矩阵。

本文研究的椭球类型为 $\epsilon \left[t\right]=\epsilon \left(q\left(t\right),Q\left(t\right)\right)$，初始椭球表示为 $\epsilon \left[t_0\right]=\epsilon \left(q^0,Q^0\right)$，目标集 $\mathcal{M}$ 是目标椭球 $\epsilon \left(m,M\right)$ 的邻域，即

$\mathcal{M}=\left\{\left(q,Q\right):\langle q-m,q-m\rangle +\left[Q-M,Q-M\right]\le {\omega }^2,0<\omega <1\right\},$ (3)

其中 $\left[·,·\right]$ 表示矩阵内积。

我们要解决的问题是寻找控制 $u\left(t\right)$ 、 $U\left(t\right)$，使得目标函数最小，即

$\begin{array}{c}\Psi \left(t_0,q^0,Q^0|\beta \text{,}u(\cdot ),U(\cdot )\right)={\displaystyle {\int }_{t_0}^{\theta }\left[U\left(t\right),U\left(t\right)\right]\text{d}t}+\left[\left(Q\left(\theta \right)-M\right),\left(Q\left(\theta \right)-M\right)\right]\\ +{\displaystyle {\int }_{t_0}^{\theta }\langle u\left(t\right),u\left(t\right)\rangle \text{d}t}+\langle q\left(\theta \right)-m,q\left(\theta \right)-m\rangle \\ =\underset{u,U}{\min }.\end{array}$ (4)

使得椭球体能够在控制的作用下从初始状态运动到目标椭球。

3. 具有随机扰动的椭球系统

在现实集群运动中，我们忽略风、空气对流等扰动因素对集群内部每个成员的影响。当集群内部成员较多时，对每个成员在避免相互碰撞又共同向既定目标运动的情形下加入扰动的刻画是非常复杂的，我们考虑扰动因素对集群外部的椭球体影响。基于这样的背景，寻找集群的最优控制 $u_1\left(t\right),U_1\left(t\right)$。

考察定义在时间区间 $\left[t_0,\theta \right]$ 上的线性时变系统，对椭球中心 $q_1$ 与构型矩阵 $Q_1$ 的方程分别加入扰动 $f\left(t\right)$ 、 $F\left(t\right)$，那么运动方程可以表述为

${\stackrel{\dot{}}{q}}_1\left(t\right)=A_1\left(t\right)q_1+C_1\left(t\right)u_1\left(t\right)+f\left(t\right),q\left(t_0\right)=q^0,$ (5)

${\stackrel{\dot{}}{Q}}_1\left(t\right)=T_1\left(t\right)Q_1+{Q^{\prime }}_1{T}_1\left(t\right)+B_1\left(t\right)U_1\left(t\right){B^{\prime }}_1\left(t\right)+F\left(t\right),Q_1\left(t_0\right)=Q_1^0,$ (6)

目标椭球表示为 $\epsilon \left(m_f,M_F\right)$。

定义具有随机扰动的椭球系统的目标函数为

$\begin{array}{l}{\Psi }_1\left(t_0,q_1{}^0,Q_1{}^0|\beta ,u_1(\cdot ),U_1(\cdot )\right)\\ ={\displaystyle {\int }_{t_0}^{\theta }\beta \left[U_1\left(t\right),U_1\left(t\right)\right]\text{d}t}+\left[\left(Q_1\left(\theta \right)-M_F\right),\left(Q_1\left(\theta \right)-M_F\right)\right]\\ +{\displaystyle {\int }_{t_0}^{\theta }\langle u_1\left(t\right),u_1\left(t\right)\rangle \text{d}t}+\langle q_1\left(\theta \right)-m_f,q_1\left(\theta \right)-m_f\rangle \\ =\underset{u,U}{\min }.\end{array}$ (7)

为简化矩阵运算，按照文献 [10] 的思想方法，将矩阵转化为向量，设矩阵 $E={\left(e_{ij}\right)}_{n\times n}$ 改写后形式为

$\bar{E}={\left[e_{11},e_{12},\cdots ,e_{1n},e_{21},e_{22},\cdots ,e_{2n},\cdots ,e_{n1},e_{n2},\cdots ,e_{nn}\right]}^{\prime }.$

引入Kronecker积(也称张量积，符号表示为 $\otimes$ )，矩阵 $E\in {ℝ}^{m\times n}$ 和矩阵 $J\in {ℝ}^{r\times s}$ 的Kronecker积是一个 $mr\times ns$ 的分块矩阵，即

$E\otimes J=\left[\begin{array}{ccc}{e}_{11}J& \cdots & e_{1n}J\\ ⋮& \ddots & ⋮\\ e_{m1}J& \cdots & e_{mn}J\end{array}\right],$

那么运动方程可以表述为

${\stackrel{\dot{}}{q}}_1\left(t\right)=A_1\left(t\right)q_1+C_1\left(t\right)u_1\left(t\right)+f\left(t\right),q_1\left(t_0\right)=q_1{}^0,$ (8)

${\stackrel{\dot{}}{\bar{Q}}}_1\left(t\right)=\left(T_1\left(t\right)\otimes I\right){\bar{Q}}_1\left(t\right)+\left(I\otimes T_1\left(t\right)\right){\bar{Q}}_1\left(t\right)+\left(B_1\left(t\right)\otimes B_1\left(t\right)\right){\bar{U}}_1\left(t\right)+\bar{F}\left(t\right),{\bar{Q}}_1\left(t_0\right)={\bar{Q}}_1^0.$ (9)

该问题的值函数为

$\begin{array}{c}{V}_1\left(t,q_1,{\bar{Q}}_1\right)=\underset{u_1,{\bar{U}}_1}{\min }\left\{{\Psi }_1\left(t,q_1,{\bar{Q}}_1|{\beta }_1,u_1,U_1\right)\right\}\\ =\underset{u_1,{\bar{U}}_1}{\min }{\displaystyle {\int }_{t_0}^{\theta }{\beta }_1\langle {\bar{U}}_1\left(t\right),{\bar{U}}_1\left(t\right)\rangle }+\langle u_1\left(t\right),u_1\left(t\right)\rangle \text{d}t+\langle q_1\left(\theta \right)-m_f,q_1\left(\theta \right)-m_f\rangle \\ +\langle {\bar{Q}}_1\left(\theta \right),{\bar{Q}}_1\left(\theta \right)\rangle -2\langle {\bar{Q}}_1\left(\theta \right),{\bar{M}}_F\rangle +\langle {\bar{M}}_F,{\bar{M}}_F\rangle ,\end{array}$ (10)

边界条件为

$V_1\left(\theta ,q_1,{\bar{Q}}_1\right)=\langle q_1\left(\theta \right)-m_f,q_1\left(\theta \right)-m_f\rangle +\langle {\bar{Q}}_1\left(\theta \right),{\bar{Q}}_1\left(\theta \right)\rangle -2\langle {\bar{Q}}_1\left(\theta \right),{\bar{M}}_F\rangle +\langle {\bar{M}}_F,{\bar{M}}_F\rangle .$ (11)

得到Hamilton-Jacobi-Bellman方程为

$\begin{array}{l}\frac{\partial V_1}{\partial t}+\underset{u_1,{\bar{U}}_1}{\min }\{\langle \frac{\partial V_1}{\partial q_1},A_1\left(t\right)q+C_1\left(t\right)u_1\left(t\right)+f\left(t\right)\rangle +\langle \frac{\partial V_1}{\partial {\bar{Q}}_1},\left(T_1\left(t\right)\otimes I\right){\bar{Q}}_1+\left(I\otimes T_1\left(t\right)\right){\bar{Q}}_1+\bar{F}\left(t\right)\rangle \\ +\langle \frac{\partial V_1}{\partial {\bar{Q}}_1},\left(B_1\left(t\right)\otimes B_1\left(t\right)\right){\bar{U}}_1\left(t\right)\rangle +\beta \langle {\bar{U}}_1\left(t\right),{\bar{U}}_1\left(t\right)\rangle +\langle u_1\left(t\right),u_1\left(t\right)\rangle \}=0.\end{array}$ (12)

那么(10)式为(12)式HJB方程的解 [11]，将(12)式第二项括号内的部分记为H，

$\begin{array}{c}H=\langle \frac{\partial V_1}{\partial q_1},A_1\left(t\right)q+C_1\left(t\right)u_1\left(t\right)+f\left(t\right)\rangle +\langle \frac{\partial V_1}{\partial {\bar{Q}}_1},\left(T_1\left(t\right)\otimes I\right){\bar{Q}}_1+\left(I\otimes T_1\left(t\right)\right){\bar{Q}}_1+\bar{F}\left(t\right)\rangle \\ +\langle \frac{\partial V_1}{\partial {\bar{Q}}_1},\left(B_1\left(t\right)\otimes B_1\left(t\right)\right){\bar{U}}_1\left(t\right)\rangle +\beta \langle {\bar{U}}_1\left(t\right),{\bar{U}}_1\left(t\right)\rangle +\langle u_1\left(t\right),u_1\left(t\right)\rangle \end{array}$

并对H分别关于 $u_1,{\bar{U}}_1$ 求偏导，即

$\frac{\partial {\left(\frac{\partial V_1}{\partial q_1}\right)}^{\prime }{C}_1\left(t\right)u_1\left(t\right)}{\partial u_1}+\frac{\partial {u^{\prime }}_1\left(t\right)u_1\left(t\right)}{\partial u_1}={C^{\prime }}_1\left(t\right)\frac{\partial V_1}{\partial q_1}+2u_1\left(t\right)=0,$

$\frac{\partial {\left(\frac{\partial V_1}{\partial {\bar{Q}}_1}\right)}^{\prime }{\left(B_1\left(t\right)\otimes B_1\left(t\right)\right)}^{\prime }{\bar{U}}_1\left(t\right)}{\partial {\bar{U}}_1}+\frac{\partial {{\bar{U}}^{\prime }}_1\left(t\right){\bar{U}}_1\left(t\right)}{\partial {\bar{U}}_1}={B^{\prime }}_1\left(t\right)\frac{\partial V_1}{\partial {\bar{Q}}_1}{B}_1\left(t\right)+2\beta {\bar{U}}_1\left(t\right)=0,$

得到最优控制 $u_1,{\bar{U}}_1$，如下

$u_1\left(t\right)=-\frac{1}{2}{C^{\prime }}_1\left(t\right)\frac{\partial V_1}{\partial q_1},$ (13)

${\bar{U}}_1\left(t\right)=-\frac{1}{2\beta }{\left(B_1\left(t\right)\otimes B_1\left(t\right)\right)}^{\prime }\frac{\partial V_1}{\partial {\bar{Q}}_1}.$ (14)

将最优控制(13)、(14)式代入Hamilton-Jacobi-Bellman方程，此时的控制 $u_1,{\bar{U}}_1$ 是使目标函数最小的控制，则(12)式变为

$\begin{array}{l}\frac{\partial V_1}{\partial t}+\langle \frac{\partial V_1}{\partial {\bar{Q}}_1},\left(T_1\left(t\right)\otimes I\right){\bar{Q}}_1+\left(I\otimes T_1\left(t\right)\right){\bar{Q}}_1+\left(B_1\left(t\right)\otimes B_1\left(t\right)\right){\bar{U}}_1\left(t\right)+\bar{F}\left(t\right)\rangle +\beta \langle {\bar{U}}_1\left(t\right),{\bar{U}}_1\left(t\right)\rangle \\ +\langle \frac{\partial V_1}{\partial q_1},A_1\left(t\right)q_1+C_1\left(t\right)u_1\left(t\right)+f\left(t\right)\rangle +\langle u_1\left(t\right),u_1\left(t\right)\rangle \\ =\frac{\partial V_1}{\partial t}+\langle \frac{\partial V_1}{\partial {\bar{Q}}_1},\left(T_1\left(t\right)\otimes I\right){\bar{Q}}_1+\left(I\otimes T_1\left(t\right)\right){\bar{Q}}_1+\left(B_1\left(t\right)\otimes B_1\left(t\right)\cdot \left(\frac{-1}{2\beta }{\left(B_1\left(t\right)\otimes B_1\left(t\right)\right)}^{\prime }\right)\frac{\partial V_1}{\partial {\bar{Q}}_1}\right)\rangle \\ +\langle \frac{-1}{2\beta }{\left(B_1\left(t\right)\otimes B_1\left(t\right)\right)}^{\prime }\frac{\partial V_1}{\partial {\bar{Q}}_1},\frac{-1}{2\beta }{\left(B_1\left(t\right)\otimes B_1\left(t\right)\right)}^{\prime }\frac{\partial V_1}{\partial {\bar{Q}}_1}\rangle +\langle \frac{-1}{2}{C^{\prime }}_1\left(t\right)\frac{\partial V_1}{\partial q_1},\frac{-1}{2}{C^{\prime }}_1\left(t\right)\frac{\partial V_1}{\partial q_1}\rangle \\ +\langle \frac{\partial V_1}{\partial q_1},A_1\left(t\right)q_1+C_1\left(t\right)\cdot \left(\frac{-1}{2}{C^{\prime }}_1\left(t\right)\frac{\partial V_1}{\partial q_1}\right)+f\left(t\right)\rangle +\langle \frac{\partial V_1}{\partial {\bar{Q}}_1},\bar{F}\left(t\right)\rangle =0.\end{array}$ (15)

由(15)式可知，值函数是关于椭球中心 $q_1$ 和构型矩阵 ${\bar{Q}}_1$ 的二次形式，由此构造线性矩阵系统二次形式的值函数，如下式

$V_{E_1}\left(t,q_1,{\bar{Q}}_1\right)=\langle {\bar{Q}}_1,P_1\left(t\right){\bar{Q}}_1\rangle +\langle q_1,p_1\left(t\right)q_1\rangle +\langle {\bar{Q}}_1,K_1\left(t\right)\rangle +\langle q_1,k_1\left(t\right)\rangle +r_1\left(t\right),$ (16)

其中 $P_1\left(t\right)=P_1\left(t\right)\otimes I$， $K_1\left(t\right)={\bar{K}}_1\left(t\right)$， $P_1\left(t\right)={P^{\prime }}_1\left(t\right)>0$，且 $P_1\left(t\right)$ 、 $p_1\left(t\right)$ 、 ${\bar{K}}_1\left(t\right)$ 、 $k_1\left(t\right)$ 、 $r_1\left(t\right)$ 均关于时间t连续可微。

关于值函数 $V_{E_1}\left(t,q_1,{\bar{Q}}_1\right)$ 分别对t、 $q_1$ 、 ${\bar{Q}}_1$ 求偏导得

$\frac{\partial V_{E_1}}{\partial t}=\langle {\bar{Q}}_1,{\stackrel{\dot{}}{P}}_1\left(t\right){\bar{Q}}_1\rangle +\langle q_1,{\stackrel{\dot{}}{p}}_1\left(t\right)q_1\rangle +\langle {\bar{Q}}_1,{\stackrel{\dot{}}{K}}_1(t)\rangle +\langle q_1,{\stackrel{\dot{}}{k}}_1\left(t\right)\rangle +{\stackrel{\dot{}}{r}}_1\left(t\right),$ (17)

$\frac{\partial V_{E_1}}{\partial q_1}=2p_1\left(t\right)q_1+k_1\left(t\right),$ (18)

$\frac{\partial V_{E_1}}{\partial {\bar{Q}}_1}=2P_1\left(t\right){\bar{Q}}_1+K_1\left(t\right),$ (19)

此时最优控制变为

$u_1\left(t\right)=-\frac{1}{2}{C^{\prime }}_1\left(t\right)\left(2p_1\left(t\right)q_1+k_1\left(t\right)\right),$ (20)

${\bar{U}}_1\left(t\right)=-\frac{1}{2\beta }{\left(B_1\left(t\right)\otimes B_1\left(t\right)\right)}^{\prime }\left(2P_1\left(t\right){\bar{Q}}_1+K_1\left(t\right)\right).$ (21)

并且记

$\begin{array}{l}{A}_1\left(t\right)=T_1\left(t\right)\otimes I+I\otimes T_1\left(t\right),\\ B_1\left(t\right)=B_1\left(t\right)\otimes B_1\left(t\right),\\ F\left(t\right)=\bar{F}\left(t\right),M_F={\bar{M}}_F.\end{array}$ (22)

将(11)、(17)、(18)、(19)、(22)式代入(15)式得到关于值函数 $V_{E_1}\left(t,q_1,{\bar{Q}}_1\right)$ 的各未知参数的一组微分方程，如下

$\begin{array}{l}{\stackrel{\dot{}}{p}}_1\left(t\right)+2p_1^{\text{T}}\left(t\right)A_1\left(t\right)-p_1^{\text{T}}\left(t\right)C_1\left(t\right){C^{\prime }}_1\left(t\right)p_1\left(t\right)=0,\\ {\stackrel{\dot{}}{k}}_1\left(t\right)+2p_1^{\text{T}}\left(t\right)f\left(t\right)+k_1^{\text{T}}\left(t\right)A_1\left(t\right)-p_1^{\text{T}}\left(t\right)C_1\left(t\right){C^{\prime }}_1\left(t\right)k_1\left(t\right)=0,\\ {\stackrel{\dot{}}{P}}_1\left(t\right)+2{P^{\prime }}_1\left(t\right)A_1\left(t\right)-\frac{1}{\beta }{P^{\prime }}_1\left(t\right)B_1\left(t\right){B^{\prime }}_1\left(t\right)P_1\left(t\right)=0,\\ {\stackrel{\dot{}}{K}}_1\left(t\right)+2{P^{\prime }}_1\left(t\right)F\left(t\right)+{K^{\prime }}_1\left(t\right)A_1\left(t\right)-\frac{1}{\beta }{P^{\prime }}_1\left(t\right)B_1\left(t\right){B^{\prime }}_1\left(t\right)K_1\left(t\right)=0,\\ {\stackrel{\dot{}}{r}}_1\left(t\right)+k_1^{\text{T}}\left(t\right)f\left(t\right)+{K^{\prime }}_1\left(t\right)F\left(t\right)-\frac{1}{4}{k}_1^{\text{T}}\left(t\right)C_1\left(t\right){C^{\prime }}_1\left(t\right)k_1\left(t\right)-\frac{1}{4\beta }{K^{\prime }}_1\left(t\right)B_1\left(t\right){B^{\prime }}_1\left(t\right)K_1\left(t\right)=0.\end{array}$

其中 $p_1\left(\theta \right)=I$， $k_1\left(\theta \right)=-2m_f$， $P_1\left(\theta \right)=I$， $K_1\left(\theta \right)=-2M_F$， $r_1\left(\theta \right)={m^{\prime }}_f{m}_f+{M^{\prime }}_F{M}_F$。

观察上述微分方程组，其中涉及非线性项，通常我们无法求出解析解，因此本文考虑用数值方法逼近。选取合适的步长，将时间离散化，给定终端时刻各参数的值，运用隐式欧拉法得到对应每个时刻参数 $P_1$ 、 $p_1$ 、 $K_1$ 、 $k_1$ 的值，运用显式欧拉法得到最优控制 $u_1$ 、 ${\bar{U}}_1$，从而 ${\stackrel{\dot{}}{q}}_1$ 、 ${\stackrel{\dot{}}{\bar{Q}}}_1$ 可解，最后使用Matlab软件进行数值模拟得到椭球轨迹管。

4. 数值仿真

本节将给出上述两个椭球系统的数值算例，时间区间取 $t\in \left[0,1\right]$，运动方程中各矩阵函数分别为

$A\left(t\right)=\left[\begin{array}{cc}0.916t& 0\\ 0& 0.916t\end{array}\right],B\left(t\right)=\left[\begin{array}{cc}\cos \left(\pi t\right)& -\sin \left(\pi t\right)\\ \sin \left(\pi t\right)& \cos \left(\pi t\right)\end{array}\right],$

$C\left(t\right)=\left[\begin{array}{cc}1.011t& t\\ t& 1.011t\end{array}\right],T\left(t\right)=\left[\begin{array}{cc}-4.021t& 0\\ 0& -4.021t\end{array}\right],$

$A_1\left(t\right)=\left[\begin{array}{cc}0.916t& 0\\ 0& 0.916t\end{array}\right],B_1\left(t\right)=\left[\begin{array}{cc}\cos \left(\pi t\right)& -\sin \left(\pi t\right)\\ \sin \left(\pi t\right)& \cos \left(\pi t\right)\end{array}\right],$

$C_1\left(t\right)=\left[\begin{array}{cc}1.011t& t\\ t& 1.011t\end{array}\right],T_1\left(t\right)=\left[\begin{array}{cc}-4.021t& 0\\ 0& -4.021t\end{array}\right].$

两个椭球控制系统的初始椭圆 $\epsilon \left(q^0,Q^0\right)$ 和 ${\epsilon }_1\left(q_1^0,Q_1^0\right)$ 、目标椭圆 $\epsilon \left(m,M\right)$ 和 $\epsilon \left(m_f,M_F\right)$ 分别为

$\begin{array}{l}{q}^0=\left[0,0\right],Q^0=\left[\begin{array}{cc}1& -1\\ -1& 2\end{array}\right],m=\left[\begin{array}{cc}1& 1\end{array}\right],M=\left[\begin{array}{cc}1& -1\\ -1& 2\end{array}\right],\\ q_1{}^0=\left[0,0\right],Q_1{}^0=\left[\begin{array}{cc}1& -1\\ -1& 2\end{array}\right],m_f=\left[\begin{array}{cc}1& 1\end{array}\right],M_F=\left[\begin{array}{cc}1& -1\\ -1& 2\end{array}\right].\end{array}$

值函数中参数取 $\beta =0.059,{\beta }_1=0.059$，扰动 $f\left(t\right)$ 和 $F\left(t\right)$ 均取随机变量，服从正态分布 $N\left(0,3\right)$，数值仿真结果如图1所示。

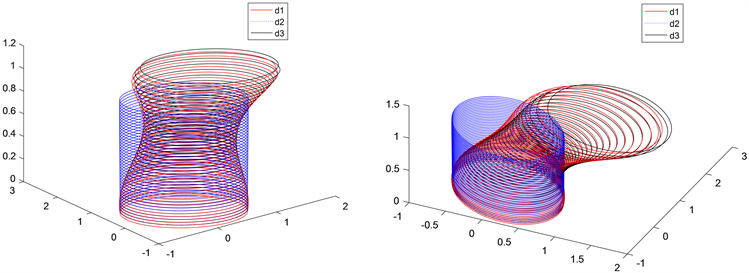
Figure 1. Comparison of ellipsoid motion with and without disturbance

图1. 有无扰动的椭球运动对比

图1刻画有无扰动的椭球运动，底面相交两轴表示初始椭圆所在的平面，与底面垂直的轴为时间轴。由d1形成的是系统加入随机扰动后的椭圆轨迹管，由d2形成的是初始椭圆无任何约束下形成的初始轨迹管，由d3形成的是无扰动时椭圆轨迹管。加入扰动项后，具有扰动的椭球系统以向左偏离的轨迹到达目标集。两个系统在 $\theta =1$ 时的椭圆切面 $\epsilon \left(q\left(1\right),Q\left(1\right)\right)$ 和 ${\epsilon }_1\left(q_1\left(1\right),Q_1\left(1\right)\right)$ 分别为

$q\left(1\right)=\left[\begin{array}{cc}1.0070& 1.0069\end{array}\right],Q\left(1\right)=\left[\begin{array}{cc}1.3273& -1.4378\\ -1.3115& 2.5248\end{array}\right],$

$q_1\left(1\right)=\left[\begin{array}{cc}0.9661& 0.9661\end{array}\right],Q_1\left(1\right)=\left[\begin{array}{cc}1.3280& -1.4645\\ -1.3745& 2.5352\end{array}\right].$

5. 结果分析

本文考察了二维情形下的系统，基本椭球系统的终端椭圆切面的中心与目标椭圆的中心几乎重合，二者构型矩阵之间的差距较小。由(3)式，目标集是椭球 $\epsilon \left(m,M\right)$ 的邻域，基本椭球系统的终端椭圆切面与目标椭圆满足关系式

$\begin{array}{l}\langle q\left(1\right)-m,q\left(1\right)-m\rangle +\left[Q\left(1\right)-M,Q\left(1\right)-M\right]\\ ={0.007}^2+{0.0069}^2+{0.3273}^2+{\left(-0.4378\right)}^2+{\left(-0.3115\right)}^2+{0.5248}^2\\ \approx 0.6711<1,\end{array}$

通过计算，无扰动的情形下基本椭球系统的终端椭圆切面位于目标椭圆的邻域内，表明我们研究的椭球在最优控制下到达了既定的目标集，验证了本文数值算法的合理性。

同样地，具有随机扰动的椭球系统终端椭圆切面的中心与目标椭圆的中心差距很小，二者构型矩阵之间的差距较小。具有随机扰动的椭球系统的终端椭圆切面与目标椭圆之间满足

$\begin{array}{l}\langle q_1\left(1\right)-m_f,q_1\left(1\right)-m_f\rangle +\left[Q_1\left(1\right)-M_F,Q_1\left(1\right)-M_F\right]\\ ={\left(-0.0339\right)}^2+{\left(-0.0339\right)}^2+{0.328}^2+{\left(-0.4645\right)}^2+{\left(-0.3745\right)}^2+{0.5352}^2\\ \approx 0.8196<1\end{array}$

通过计算发现，在具有扰动的情形下，系统的终端椭圆切面同样位于目标椭圆的邻域内，这表明我们研究的椭球能够通过控制运动到达目标集。当然，在扰动较大时，我们研究的具有扰动的椭球系统终端会出现不在目标椭球邻域内的情况，此时可以通过引入脉冲控制衰减系统扰动 [12]，使得系统能够在控制的作用下到达目标集。

6. 总结

本文主要贡献是基于椭球积分给出具有随机扰动的集群控制问题的数值算法，仿真结果表明，本文的算法能够较好地实现在控制的作用下集群运动到既定目标。作者希望通过对此类问题的考察，能够为现实复杂环境中的集群运动提供思路。