1. 引言
挠度是梁或柱型结构在受力形状发生变化时,轴线在其垂直方向的上的位移 [1]。无论是在建筑、桥梁等健康评估方面还是对梁、柱型结构的材料进行弹性模量的测量方面,挠度在某种程度上反映了梁的整体竖向刚度和线性变化特征,挠度检测为评判梁或柱型结构的安全性与耐久性提供重要的依据,因此测量挠度尤为重要。目前挠度测量的传统方式有悬锤法、水准仪直接测量法,较大地受到桥上桥下环境的影响。新兴的测量方式比如倾角仪法、GPS遥感法、光电成像法、激光图像法 [2],但设备昂贵,无法实现对单一位置的桥梁或建筑结构全天候的实时监测,一些需要通过光学传感的设备会受到大气和天气等环境因素的影响从而使精度降低。随着光纤传感的发展,对以上问题提供了较好的解决方法。光纤由于其本身的特性可以很好地适用较为复杂的环境,以及其较高的测量精度可适用于大小型结构的测量 [3] [4] [5]。光纤传感器广泛应用于梁或柱型结构的弯曲 [6] 和位移 [7] 的测量以及解决形变与温度交叉问题 [8],目前分布式光纤传感 [9] 和准分布式光纤传感 [10] 在梁柱型结构中应用较多,但其测量技术与成本较为昂贵还无法大范围应用。
光纤传感始于上世纪70年代,自出现以来在诸多领域得到了发展和推广,广泛用于建筑、机械、电子仪器、航天航空、石油、化工、核工业等诸多领域 [11] [12]。光纤传感器具有抗电磁干扰,耐腐蚀,电绝缘性好等特点,光纤的体积小,质量轻,便于实现传感器的小型化。光纤应变传感器灵敏度高,分辨率高。传输损耗小,传输容量大,可传感器能够复用。以光纤布拉格光栅(Fiber Bragg Grating, FBG)为代表的传感器由于外界环境对Bragg波长的调制,通过监测波峰的漂移量来实现对外界环境变化传感的目的。
2. 简支梁挠度公式推导和仿真
2.1. 简支梁挠度理论
简支梁的两端搁置在支座上,支座仅约束梁垂直方向的位移,梁的两端可自由转动 [1]。为使整个梁不产生水平移动,在一端加设水平约束如图1中的A端,该处的支座称为铰支座,另一端不加水平约束的支座称为滚动支座如图中的B端。现有这样一个简支梁材料的弹性模量为E,截面的惯性矩为I,长为l,C点为跨中位置,D点处施加荷载以向下的压力F来代替集中荷载。设D点到左端距离为a,到右端距离为b,求解梁上任意位置x处的挠度,在这里取向下为正,所有的数值都取正值。
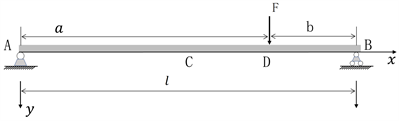
Figure 1. Diagram of simply supported beam
图1. 简支梁示意图
对于简支梁的挠度公式在材料力学、弹性力学等学科中均已给出这里直接引用。集中荷载位于AD段即
时任意位置的挠度
为
(1)
集中荷载位于BD段即
时任意位置的挠度
为
(2)
以上两式表示在施加集中载荷后简支梁上任意位置的挠度,以AD段为例求得简支梁上最大挠度
(3)
由式(3)可知在AD段最大挠度的值会随着集中荷载的位置变化而变化,不是一个确定的值,最大挠度处也不是一个确定的位置。下面计算出简支梁的跨中C点,即
处挠度的值为
(4)
2.2. 简支梁跨中挠度仿真
在这里我们采用有限元分析软件Workbench对荷载处于简支梁上不同位置时梁的挠度情况进行分析,模拟参数如表1所示。
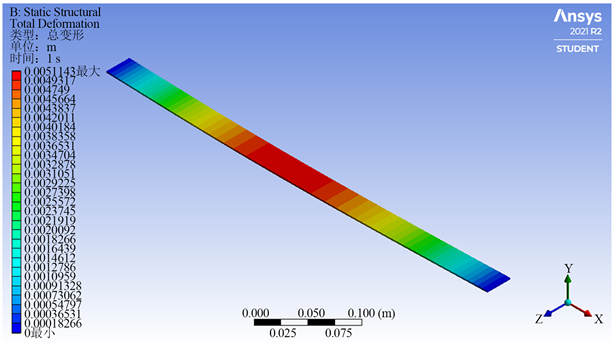
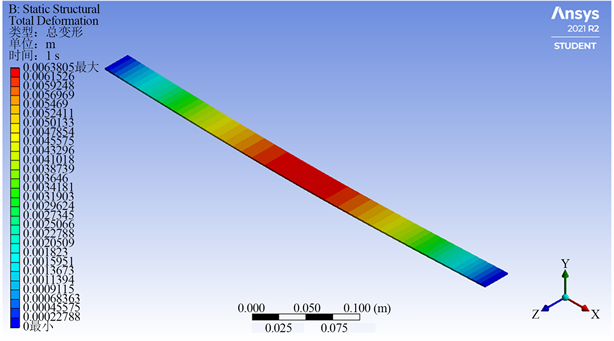
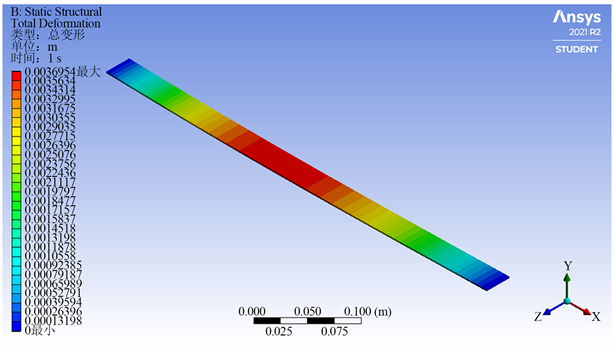
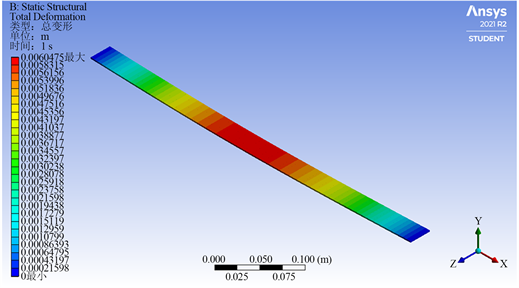
Figure 2. Diagram of simply supported beam
图2. 简支梁示意图
通过软件模拟得到简支梁的示意图,部分如图2所示,图中红色位置表示挠度最大处,蓝色表示挠度最小处,可以发现最大挠度处处于跨中附近,可以看出在
端上受任意荷载的简支梁,只要挠曲线上没有拐点均可近似的将梁中点的作为最大挠度处。通过以上计算发现,当荷载非常接近简支梁的端点时,简支梁的跨中挠度和最大挠度有2.6549%的误差,而当荷载越靠近中点误差越小只有0.0046%的误差。跨中是一个特殊位置可以在实验前可以提前测量得知,并不受实验过程中变量的影响,所以将中点看作最大挠度处并将测量点放在跨中位置可大大降低实验中计算难度和测量难度。
可以得到梁上任意位置施加荷载时跨中处的挠度方程,
时
(5)
时
(6)
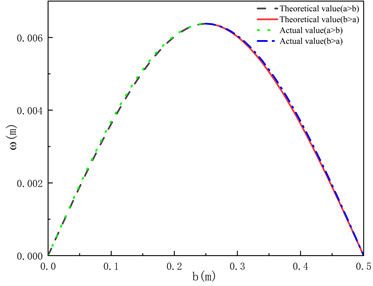
Figure 3. (a) Relationship between load position and mid-span deflection of simply supported beam with 9.8 N load; (b) Comparison between theoretical value and actual maximum deflection of simply supported beam mid-span deflection
图3. (a) 简支梁荷载为9.8 N时,荷载位置与跨中挠度的关系;(b) 简支梁跨中挠度的理论值与实际最大挠度值的对比
根据式(5)和式(6)可以画出跨中位置处挠度的理论值图像如图3(a)所示,并与实际最大挠度对比如图3(b)所示。通过以上两图和计算可知跨中挠度和实际最大挠度相差不大,在测量时可以以跨中位置的挠度来代替实际最大挠度。
3. FBG对简支梁跨中挠度测量的实验研究
3.1. 简支梁跨中挠度与FBG应变关系推导
FBG的谐振方程
,
为谐振波长,
为光栅的有效折射率,
为光栅的周期。光栅的有效折射率和周期的变化都会引起谐振波长的变化,因此可以影响有效折射率和周期的物理量如应变或温度都可以通过FBG进行测量 [13]。对于应变和温度引起的波长变化量
可表示为
(7)
式中
为光纤的光弹系数对于石英光纤可取0.217,
为应变的变化量,
为光纤的热光系数可取6.34 × 10−6/℃,
为温度的变化量。
通过进行力学分析得到FBG的应变与梁的挠度的关系,在梁上截取一小段如图4,长为L,厚为h,根据平面假设,在变形过程中,变形前为平面的横截面变形后仍保持为平面且与变形后梁的轴线垂直 [14] [15],变形后各自绕中轴线相对旋转角度为
。
变形前后中轴线上的长度不变,中轴线上梁的应变
可以写为
(8)
这里可以假设FBG的应变和梁的应变是相等的,但是在实际中还要考虑光纤本身的半径和粘贴的厚度,但是这些在测量时并不方便而且在涂抹胶时并不能保证每个部分都是均匀的厚度,在这里我们可以假设FBG的应变为
(9)
其中的k值与光纤半径和粘贴厚度有关 [7] [16],简支梁在发生形变时,对应的跨中位置在竖直方向发生的位移可近似的看作该点的挠度w,可通过图3进行计算得
(10)
通过泰勒级数展开并消去影响较小的高阶次项,使用FBG的应变来表达梁的挠度公式
(11)
可以发现梁的跨中挠度和FBG的应变是正比例关系,且比例系数是和梁本身还有FBG的粘贴情况有关,所以上式可以简单的表达为
(12)
通过实验测量FBG的波长漂移量来计算FBG的应变,计算应变和跨中挠度的比值来确定两者间的比例系数。
3.2. 准备实验
考虑到FBG的栅区的没有涂覆层保护是非常脆弱的,如果栅区弯曲过大会造成FBG的损坏,在粘贴时出于保护实验装置的目的将整个栅区都用胶粘贴到梁的底部。FBG在室温下谐振波长为1549 nm,栅区长度为10 mm,光纤类型为SMF-28e,反射率大于85%,带宽小于0.25 nm。
第一步:在简支梁上画出等距的标记,每隔10 mm做出标记作为梁上的施力位置。
第二步:粘贴FBG,先在简支梁上标记出跨中位置,并在距离跨中位置左右各2 cm处和上下各0.5 cm处粘贴电工胶带,用胶带围出一个4 cm × 1 cm的空,将FBG栅区中间对准跨中位置,左右两端固定,固定时给FBG施加一个很小的预应力,排除由于光栅位置弯曲而带来的误差。使用AB胶涂满留出的空,并用刮板刮平AB胶,等AB胶将要固化时撕去胶带,这样就能留下一个如图5的粘贴形状规则厚度均匀的粘贴式FBG传感器。
第三步:搭建简支梁模型,采用悬挂重物的方式来模拟集中荷载在简支梁上的作用。每隔10 mm作为一个测量点。
第四步:重物在梁上反复移动,并用砂纸打磨简支梁的边缘使其光滑防止在实验过程中由于悬挂重物的绳子与梁有摩擦力影响绳子的移动从而造成测量误差。
第五步:组装简支梁挠度测量的检测系统,主要实验仪器有放大自发辐射光源(Amplified Spontaneous Emission, ASE),可以输出10 mW功率波长在1525~1600 nm的范围内高稳定的光。光谱仪(Optical Spectrum Analyzer, OSA),波长扫描范围为600~1700 nm,最大波长分辨率为0.02 nm。以及粘贴好的FBG应变传感器。在这里我们使用透射式的传感方式因为透射式相较于反射式可以消除由于光纤端面反射和熔接损耗带来的波形噪声,尽可能地保证波形的完整性更方便观察波长的漂移情况。如图6中的连接方式。

Figure 6. Detection system for mid-span deflection measurement of simply supported beam
图6. 简支梁跨中挠度测量的检测系统
3.3. 测量实验
实验开始前将实验装置放在同一温度场中两小时以上,这样可以排除实验过程中实验材料温度不均的影响,将光谱仪开机后需预热一小时左右后进行波长校准,防止光谱仪长时间放置对测量结果造成影响。
使用9.8 N的荷载在梁上标注的位置进行逐一测量,参考图1中的b值,荷载从0到500 mm,每间隔10 mm进行一次测量得到跨中位置应变的透射光谱图,实验在室内进行温度未发生较大变化,在这里不考虑温度的影响。

Figure 7. Transmission spectrum of FBG when the load is at different positions on the simply supported beam
图7. 荷载在简支梁上不同位置时FBG的透射光谱图
由图7中透射光谱图中的Bragg峰的变化计算出对应的应变,并和图1中简支梁上载荷位置b建立关系。通过数据处理软件可以画出简支梁上载荷位置与应变之间的关系如图8(a),
时拟合出的曲线
,与图3(a)中的理论挠度值之间的比例系数为
,
时拟合出的曲线
,与理论挠度值之间的比例系数为
,两边存在0.013的差值。此外我们又以不同的荷载做了对比试验,分别以4.9 N、7.35 N、12.25 N和14.70 N的荷载在简支梁上进行实验,通过Bragg的波长漂移量计算FBG的应变,得到不同荷载下荷载位置与FBG的应变的关系如图8(b)所示,并根据理论值拟合出相关曲线。将上边结果用表格表示,如表2所示。
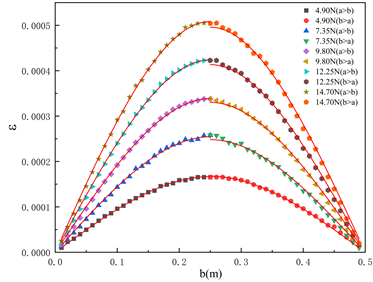
Figure 8. (a) Relationship between load position and FBG strain on simply supported beam; (b) Mid-span deflection and fitting curve of simply supported beam under different loads
图8. (a) 简支梁上荷载位置与FBG应变的关系;(b) 不同荷载下的简支梁跨中挠度和拟合曲线

Table 2. The mid-span deflection measurement experiment of simply supported beam under different loads
表2. 不同荷载下的简支梁跨中挠度测量实验
4. 结论
挠度检测为评判梁或柱型结构的安全性与耐久性提供重要的依据,因此测量挠度尤为重要。光纤光栅有着对应变高度敏感的特性,可以通过谐振波长的漂移量来计算应变并通过转换用于测量梁的挠度,此方法具有提高测量精度、保障测量的稳定性的特点。本文应用FBG对简支梁和两端固支梁的跨中进行了挠度测量,并引入了荷载位置这一参量,通过计算证明了简支梁跨中挠度和实际最大挠度会随着荷载到跨中的距离远近有2.6549%到0.0046%的误差。在误差允许的范围内适合使用在跨中位置粘贴FBG应变传感器的方式进行测量。以9.8 N荷载为例,测量结果计算出FBG应变值的数据拟合曲线和跨中理论挠度值曲线的相关度达到0.99945和0.99786,计算的应变值和挠度的理论值的比例系数分别为0.05306和0.05176,我们分析引起这一误差的原因其一是在粘贴FBG时造成的人为误差,其二在较靠近跨中的位置测量时谐振波的峰值变化量不大,光谱仪的测量精度不能区分,造成了越靠近跨中位置前后间隔的两个点波长漂移量相近或者相同。本次研究证明了荷载位置确实会对简支梁跨中挠度的测量有影响以及在跨中位置安装测量点可以对整个梁进行粗略地监测,对今后进行挠度测量时安装FBG传感器的位置以及进行准分布式测量时安装传感器的距离提供一定的理论参考。
NOTES
*通讯作者。