直线图形剪拼的基本数学活动案例

Basic Mathematical Activity Cases of Straight Line Graphics Cutting and Splicing

摘要: 义务教育数学课程标准中提出了培养学生基本数学活动经验的要求，但在教学实践中构建良好的数学活动往往是一大挑战。三角形和特殊四边形是初中阶段的基本直线形，在不同条件下如何实现这些图形的转化一直是数学中令人感兴趣的问题。在计算与推理基础上利用图形剪拼不仅可以实现这些重要图形的转化，并且也提供了一个融手脑并用、几何直观和逻辑推理于一体的活动范例。既增加学生动手操作实践经验，也可以深化学生对于几何知识的理解，感受“数学活动”的独特魅力。

Abstract: Compulsory education mathematics curriculum standards put forward the requirements of cultivating students’ experience in basic mathematics activities, but constructing good mathematics activities in teaching practice is often a big challenge. Triangles and special quadrilaterals are the basic straight lines in junior high school. How to realize the transformation of these figures under different conditions has always been an interesting problem in mathematics. On the basis of calculation and reasoning, the use of graph cutting and spelling can not only realize the transformation of these important graphs, but also provide an activity paradigm that integrates hand and brain, geometric intuition and logical reasoning. It not only increases students’ hands-on experience, but also deepens students’ understanding of geometric knowledge and feels the unique charm of “mathematical activities”.

1. 前言

与数学基本知识和数学基本技能不同，基本数学活动经验需要在一项项整体性、综合性的活动中让学生亲身感悟与思考，并且不断积累，最终形成自己的数学理解。史宁中教授在2006~2007年数学教育高级研讨班中就提出应加强对于学生“基本数学活动经验”的关注 [1]，认为其与学生的学习过程、情感、情境创设等息息相关，在教学中应加以重视。国家在《义务教育数学课程标准(2011年版)》中则明确将基本活动经验作为课程目标而设定，同时将其应用于综合与实践这一内容领域 [2]。对于数学活动经验，存在不同的看法，有学者认为活动指的是具体的动手操作活动，亦有学者认为活动指的是思维活动 [3]。孔凡哲认为数学活动经验实质指的是围绕特定的课程教学目标，学生经历了与学科相关的各类基本活动之后，所留下的直接感受、体验、感悟，既包括行为操作活动经验，也包括思维反思活动经验 [4]。数学活动经验需要在“做”的过程和“思考”的过程中沉淀，既需要动手活动获得直接操作性经验，也需要通过抽象、推理等思维活动获得反思性经验。

但在实际的教学过程中，教师由于时间不足、资源短缺、活动设计经验匮乏等问题，在教学中仍以大量的间接经验教授学生知识。即使在同类项、勾股定理、直角坐标系、直线(圆)与圆的位置关系等内容的教学中我们经常会看到“活动”，但往往是为活动而活动，或者活动的表面化给人“去数学化”的诟病。因此，本文以直线图形的剪拼为例，设计了一次有关几何教学的基本活动，让学生在动手操作的过程中，通过折纸活动更加深刻地体会到图形的变化和基本图形的内在关系，理解图形的基本性质，进而提高学生对于几何图形的学习兴趣，增强学生几何学习的自信心，激发学生的创造力。

2. 基本活动设计

剪拼过程从长方形不断延申、拓展至正方形，几何内容知识在面积相等的出入相补原理基础上从中位线定理到三角形全等、射影定理，最后到勾股定理，剪拼难度逐渐提高，几何知识的运用也由浅入深。既让学生在折纸的动手中获得操作性经验，也让学生在思考中获得反思性经验。下面对具体活动过程进行阐述。

准备工作：每位学生准备直尺、铅笔、本子以及十张以上长方形的纸，可折叠撕开即可。

(一) 探究活动一：请学生思考一下仅仅借助直尺、铅笔如何将一张长方形的纸张折叠剪拼为三角形？并动手操作。

学生1：将长方形沿对角线折叠撕开，而后将对边拼接在一起，即为三角形，如图1所示。

老师在此基础上继续提问：除此之外，还有其他的剪拼方法吗？试想想，剪拼前后图形的哪些地方发生了变化，哪些地方没有发生变化？

学生2：图形的边、角、形状均发生了改变，但剪拼前后图形的面积不变。

从图形的面积公式入手思考，已知 $S_{长}=ab$， $S_{三}=\frac{1}{2}{a}_{底}h$，要使得 $S_{长}=S_{三}$，可让 $a=a_{底}$， $b=\frac{1}{2}h$ 或 $a=\frac{1}{2}{a}_{底}$， $b=h$。按照两种分类将学生分成两组对长方形剪拼为三角形进行探索并展示成果，若学生无法直接进行剪拼，可让其先在纸上绘图，而后再动手操作。

Figure 1. Rectangle to isosceles triangle

图1. 长方形转等腰三角形

Figure 2. Rectangle to triangle exploration 1

图2. 长方形转三角形探索1

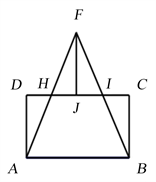
Figure 3. Rectangle to general triangle 1

图3. 长方形转一般三角形1

组1：若 $a=a_{底}$， $b=\frac{1}{2}h$，如图2所示。直线l到AB的距离为BC的2倍，在l上任取一点，与A、B所围成的三角形面积和长方形ABCD的面积均相等。但折纸操作以 $\Delta ABF$ 为最佳。

操作过程如图3所示，在CD上取两点H、I，分别沿AH、BI折叠撕开，拼接于CD的上方，即为 $\Delta ABF$。又由中位线定理可知 $HI=\frac{1}{2}AB=\frac{1}{2}CD$，因此为确定H、I两点，应先在CD上任取一点J，沿DJ、CJ分别折叠，折点即为H、I。当H与D或I与C重合，则为直角三角形。

组2：若 $a=\frac{1}{2}{a}_{底}$， $b=h$，如图4所示。延长AB至E，使得 $AE=2AB$，在直线m上任取一点，与A、B所围成的三角形面积和长方形ABCD的面积均相等。但折纸操作以 $\Delta AEF$ 为最佳。

操作过程如图5所示，将B、C两点对折，折点即为BC中点G，沿AG折叠撕开，拼接于BC的右方，即为 $\Delta AEF$。亦可思考将AB向两边延长，如图6所示，在CD上任取一点G，延长GE、GF分别与BA、AB的延长线相交于H、I，为实现折纸操作，E、F应为AD、BC的中点，将长方形ABCD沿BC对折，折点即为E、F，沿GE、GF折叠撕开，拼接于长方形ABCD的左右两边，即为 $\Delta GHI$。当G与D或C重合时，即为直角三角形。

Figure 4. Rectangle to triangle exploration 2

图4. 长方形转三角形探索2

Figure 5. Rectangle to general triangle 2

图5. 长方形转一般三角形2

Figure 6. Rectangle to general triangle 3

图6. 长方形转一般三角形3

从学生的原有认知入手，引导学生发现条件与目标之间的差异与共性，借助两者之间的共性消除差异进而连接条件与目标，逐步实现问题的解决。另外分组活动探究可激发学生的积极性，组内合作可增强学生之间的交流，提高学生的表达能力，培养学生的人际交往能力。

(二) 探究活动二：下面同学们可以试试如何将长方形剪拼为平行四边形和梯形？

老师：大家试着类比长方形转化为三角形的过程对此进行思考。

学生：长方形剪拼为平行四边形，角、形状发生了改变，但剪拼前后图形的面积、边的数量不变，而且长方形是特殊的平行四边形，若使其转变为一般的平行四边形，只需将直角转化为锐角或钝角即可。

操作过程如图7所示，在CD上任取一点E，沿AE折叠撕开，拼接于长方形ABCD的右边，即为平行四边形ABFE。

老师：那梯形呢？同学们仔细观察长方形剪拼为三角形的过程，看看可以发现什么有趣的事？

学生：在长方形剪拼为三角形的基础上，如图3、图6，若撕下的为梯形，而非三角形，则可剪拼为梯形。

操作过程可参照三角形的剪拼过程，在图3的基础上，让AF、BF分别绕H、I点逆时针、顺时针旋转适当角度，如图8所示，梯形MNOP即为剪拼后的图形。亦可在图6的基础上，让HG、IG分别绕E、F点逆时针、顺时针旋转适当角度，如图9所示，梯形MNOP即为剪拼后的图形。

Figure 7. Rectangle to parallelogram

图7. 长方形转平行四边形

Figure 8. Rectangle to Trapezoid 1

图8. 长方形转梯形1

Figure 9. Rectangle to Trapezoid 2

图9. 长方形转梯形2

在长方形剪拼为三角形的基础上，学生通过观察、类比推理等思维活动，理清解决此类问题的方法步骤，寻找知识间的关系，依据所学的知识理论动手实践操作，以此逐步实现了长方形到平行四边形和梯形的剪拼，而非盲目、无依据地简单剪拼活动操作。

(三) 探究活动三：接下来同学们再试试如何将长方形剪拼为正方形？

老师：我们仍以面积的角度思考， $S_{长}=ab$， $S_{正}=c^2$，若要使 $S_{长}=S_{正}$，则 $c^2=ab$，看到这个等式，同学们能想到与之有关的数学知识吗？

学生：射影定理。

老师：同学们可在纸上依据射影定理进行绘制，如何通过a、b得到c。

如图10所示，O为GB中点，以OB为半径作圆与AE相交于H，由射影定理可得 $AH=\sqrt{AG\times AB}$。以AH为边构造正方形，即为AHIJ，如图11所示，连接BJ分别交CD、HI于点K、L，因为 $\Delta JDK~\Delta JAB$， $\Delta BHL~\Delta BAJ$，所以 $\frac{JD}{JA}=\frac{DK}{AB}$， $\frac{BH}{AB}=\frac{LH}{JA}$，解得 $DK=a-\sqrt{ab}$， $LH=\sqrt{ab}-b$，那么 $DK=HB$， $JD=LH$，即 $\Delta JDK\cong \Delta LHB$，同理可得 $\Delta JIL\cong \Delta KCB$。因此可以此对长方形进行剪拼。

老师：现在问题转变为如何确定H、K两点？

为确定H、K两点，必须先剪裁得到一张如图10所示的拼接图形。取一张矩形纸如图12所示，使得其长为长方形的长与宽之和，宽大于长方形的长，过点A沿BG折叠，折线为 $A{A}^{\prime }$，将B、G点沿 $A{A}^{\prime }$ 向上折叠，重合点分别为E、D，过E、D沿 $A{A}^{\prime }$ 折叠，折线分别为 $F{F}^{\prime }$ 、 $C{C}^{\prime }$，沿EF、DE、CD撕开如图10，将B、G两点对折，折点为BG的中点O，过点O折叠使点B置于AE上，即为点H，沿AD撕开，在ABCD上确定H、K两点。

H、K两点确定后，如图11所示，沿BK、HL折叠撕开，拼接于长方形ABCD的上方，即为正方形AHIJ。

Figure 10. Projection theorem construction

图10. 射影定理构造

Figure 11. Rectangle to square

图11. 长方形转正方形

Figure 12. The structure of the cutting puzzle

图12. 剪拼图纸构造

长方形剪拼为正方形，类比三角形剪拼发现借助面积公式无法对其进行直接操作。解决问题的过程中遇到了瓶颈，依据波利亚的解题理论，借助其解题表设计问题，以已知探索未知，激发学生的智力活动，引导学生产生新的思路，进而对问题继续探索思考，层层深入，最终得以解决问题。

(四) 探究活动四：将两个正方形剪拼为一个正方形。

老师：同样我们以面积相等为基础及进行思考， $S_{正1}=a^2$， $S_{正2}=b^2$， $S_{正3}=c^2$，若要使得 $S_{正1}+S_{正2}=S_{正3}$，即 $a^2+b^2=c^2$，那么可由此想到什么呢？

学生：勾股定理。

老师：很好，同学们可在课下按照此思路或其他思路进行思考讨论。

以下给出两种剪拼方式仅供参考，在纸上绘制如图13所示，将正方形ABCD、AEFG剪拼为正方形DHIG，过点I作 $IJ\perp BG$ 交BG于点J，由三角形全等判定定理易得 $\Delta DLE\cong \Delta HKB$， $\Delta DCH\cong \Delta GJI$， $\Delta FLG\cong \Delta JKI$，则可据此剪拼。另外亦可借助赵爽弦图进行剪拼，如图14所示。

Figure 13. Pythagorean Theorem Application 1

图13. 勾股定理运用1

Figure 14. Pythagorean Theorem Application 2

图14. 勾股定理运用2

在教学过程中，需要给学生“留白”，让学生可进行不同程度的思考，因此最后将两个正方形剪拼为一个正方形的活动作为探索性作业，留给学生课下思考。

3. 总结

通过以上的活动可以发现，在保持面积下，利用几何直观、计算和推理能实现初中基本几何图形的转化。同时，随着基本图形转化的实现，也构建成功以直线图形的剪拼为内容的基本活动经验综合与实践活动课的整体化设计。以折纸活动贯穿始终，让学生在实际动手操作中进行思考，由浅入深、层层递进地综合运用所学知识，解决图形剪拼问题，积累基本活动经验，提高学生的数学素养。

枯燥乏味的知识会使得学生厌恶学习，而浅显易懂的活动则会使学生懒于思考，因此在设计活动时不仅要注重活动本身的趣味性、操作性，激发学生的学习兴趣，还要注重活动背后的数学价值、数学思考，让学生在动手的过程中思考，思考之后还要应用于实践操作之中。几何折纸活动就对此进行了践行，折纸活动的操作材料简单易得，图形变化生动有趣，变化之中又蕴含着几何定理知识，需要学生思考，在教师的提问引导下，学生通过观察、类比、推理等思维活动从最基础的长方形和三角形入手，延申至平行四边形、梯形，再到正方形，一步步找到问题解决的办法，最后又归于折纸活动的动手操作，在“做”和“思考”中体会数学知识，感悟数学活动经验。

需要说明的是，尽管通过实际动手操作可以丰富学生的基本活动经验，提高学生的学习兴趣，同时图形之间的剪拼也可以扩展学生的思维，培养学生的创造力。但对于学生来说，直接对图纸进行剪拼可能不太容易，因此可让其先在纸上绘图，再依据面积相等，同时借助中位线定理、三角形全等、射影定理、勾股定理等知识点实现几种图形的转化，最后根据绘图过程对图形进行剪拼，使得学生在剪拼的过程中可以进一步理解图形的性质及其所涉及的知识点，体会到图形变化的乐趣。

基金项目

教育部2021年产学合作协同育人项目——数学教师教育在线平台建设(202101301065)；新疆师范大学项目“我校教师开展课程思政胜任力调查”(SDJG2021-38)。