基于布尔代数的地图符号修正的数学模型

Mathematical Model of Map Symbol Correction Based on Boolean Algebra

摘要: 地图符号是制图对象从制图区域到地球椭球面的映射，从地球椭球面到制图主体的认知结构的映射，再到地图平面的映射的同胚象。地图符号与其指代地物的双函数关系是拓扑变换必须遵循的原则。由于地物在时空中演化的普遍性、经常性和连续性及资料的收集欠缺等原因，使编图过程总会在个别地方出现地图符号与指代地物的对应性破缺的问题，这就是地图的错误。对符号失实、遗漏、错位等错误给出了数学定义。根据具有包含关系的地图的幂集属于布尔代数系的原理，提出了基于布尔运算的修改错误符号的操作定义。以实例演算了地图从包含错误符号集的qghf(A)_A到消除错误的成图qghf(A)_B的变换过程。

Abstract: Map symbols are homeomorphic images of mapping objects from mapping regions to the earth ellipsoid, from the earth ellipsoid to the cognitive structure of mapping subjects, and then to the map plane. The relationship between map symbols and their referent objects is a principle to be followed in topological transformation. Due to the universality, regularity and continuity of the evolution of ground objects in time and space and the lack of collection of data, there is always a problem of broken correspondence between map symbols and referring ground objects in some places in the process of map compilation, which is the mistake of maps. The mathematical definition of false symbol, omission and dislocation is given. According to the principle that the power set of the map with inclusion relation belongs to the Boolean algebra system, an operation definition for modifying error symbols based on Boolean operation is proposed. An example is given to calculate the trans-formation process of map from qghf(A)_A which contains the wrong symbol set to qghf(A)_B which eliminates the error.

1. 引言

地图以反映地表宏观尺度的自然地理和人文现象为特征。无论是基于自然原因发生的自然灾害，还是人们为发展经济，改善人居环境而实施的农田规划、道路规划、城镇发展规划等，都会引发地物地貌的演化。地物演化遵循增长地物和消亡地物的代数和恒为零的演化规律 [1] [2] [3]。地图能否正确反映制图区域的地物演化状况，与地图现势性密切相关。然而，由于制图区域在时空中的演化是个连续过程，虽然不同的地物不同地区有不同的演化速率，但演化是绝对的。由于任何地图的编制，从收集和分析资料，制定编辑计划到编制作业，需要流程和时间，这样，一些在此时间发生演化的地物未能及时反映和表达就不足为奇 [4]。这也是刚编制完成，尚未审校修改的初始地图，总会存在一些错误的原因。为了确保地图的质量，使地图符号与其指代的地物一一对应，就必需对地图进行仔细的审校，及时发现错误和逐一修改。由于地图符号错误的定义及修改错误的问题鲜有文献论述，本文将对这一问题进行研究和探讨。把地图符号的错误视为其与指代地物的对应性破损，把修改错误操作视为对应性的修复，并以数学变换的形式表达，这本身就是一种理论创新。因为数学是科学思维可以定量地表达关系的语言，是科学思维确定性和精密性的必要形式 [4]。使地图符号错误及修正错误的操作获得精密的数学形式和定量描述，这是本研究的意义所在 [5]。

2. 地图符号生成的拓扑学原理和待审图的符号集合

所有地图皆与客观实际的两个基本要素有关，即位置及其上面的特征。位置仅指二维平面上的位置，例如用 $\left(x,y\right)$ 坐标表示的地点。位置上面的特征是某种性质或量值 [6]。不同专题的地图，在同一位置上选取地物的性质或量值会有所不同，例如，人口图上可选人口数，地貌图可选高程，温度分布图选温度等。地图制图表示的依据来自地学空间数据(Geospatial Data)，也即是包括资源、环境、经济和社会等一切领域的带有地理坐标(纬度 $\phi$ 和经度 $\lambda$ )的数据。由于从球面坐标 $\left(\phi ,\lambda \right)$ 到平面坐标 $\left(x,y\right)$ 的变换实质上是同胚或拓扑变换。地图上的经纬网是地球椭球面上的经纬网的同胚象。在小比例尺条件下可用圆球取代椭球，但平面坐标网依然是球面经纬网的同胚象。根据同胚的定义，受到地图投影制约的地图符号的位置，自然与其反映和表达的对象一一对应。而性质特征或量值的对应，则是通过制图者的主观干预(选择性质)来实现。而制图者地图概括(包括选取、舍弃、简化、增补等)的质量取决于其对制图物体了解和认识的程度，这就产生一个制图物体及其在球面上的投影的位置、形状、大小、事物的性质特征等先变换为制图者大脑中的相关知识的问题，这些知识必须先以观念形态存在于制图者的认知结构中。由此可见，从制图物体到地图符号的同胚的实现，是以制图者的认知结构为中介的，这样，地图符号的生成就包括了三重拓扑映射：从三维空间X到地球椭球面的映射 $f:X\to S$ ；从S到制图者认知结构Y的映射 $g:S\to Y$，从Y到二维平面Z的映射 $q:Y\to Z$。三维空间X中的制图区域A内的制图物体 $x\in A\in X$，在 $f:X\to S$ 映射下变换为 $f\left(x\right)\in f\left(A\right)\in S$，在g映射下变换为 $gf\left(x\right)\in gf\left(A\right)\in Y$，在q映射下变换为 $qgf\left(x\right)\in qgf\left(A\right)\in Z$。 $qgf\left(x\right)$ 即x的地图符号，它是制图物体x在 $f,g,q$ 三重拓扑映射下的拓扑象(同胚象)。拓扑映射及其逆变换所要求的一一对应性，确保了我们能通过地图符号 $qgf\left(x\right)$ 而获得关于x的相关知识，从而使地图具有空间认知的强大功能 [7] [8]。

一幅按某种比例尺表示的地图，或多或少地会存在一些错漏，这些错漏，主要表现为符号与其指代的地物的对应性破缺上。实地上不复存在的地物地图上仍保留着原来的符号，从而使符号表示失实；实地上已存在应予表示的地物，而地图上却没有相应的符号表示，这是表示遗漏；地图符号与表示对象存在性质或量级不符，谓之表示错误；地物的空间定位与地图符号的空间定位不一致，等等。此外，由于人为因素，使某些符号的表示与规范图式不符，也是产生错误的原因。设存在着一定的错误的未经审校、修改完善和验收之前的地图为 $qgf{\left(A\right)}_A$，在这地图上存在着两大符号集：正确符号集 $qgf{\left(A\right)}^{*}$ 和错误符号集 $qgf{\left(A\right)}^{*c}$，正确地图符号集和错误符号集互为补集 [9] [10]，即

$qgf{\left(A\right)}_A=qgf{\left(A\right)}^{*}\cup qgf{\left(A\right)}^{*c}$ (1)

错误地图符号修正的目的在于使错误符号集变换为正确符号，使正确符号集与符号全集等价：

$qgf{\left(A\right)}_A=qgf{\left(A\right)}_A{}^{*}$ (2)

式(2)是任何地图编制任务追求的结果。由于任何地图编制任务一般都是由训练有素的专业技术人员承担，所以一般情况下，错误符号集是个包含少量元素的集合。从某种意义上说，错误符号集的大小也是对编图人员的业务素质和责任心的度量。

3. 地图符号错误的定义

3.1. 定义1遗漏

若需要地图表示的地物存在而对应的符号缺失，即

$\exists x\in A\Rightarrow qgf\left(x\right)=\varnothing \in qgf{\left(A\right)}_A|x\ne \varnothing$ (3)

则称 $qgf\left(x\right)=\varnothing$ 为遗漏符号。遗漏符号需要根据实地地物的性质增补对应的符号。

3.2. 定义2符号表示错误

符号表示错误是指：

$\begin{array}{l}1)\exists qgf\left(x\right)\in qgf{\left(A\right)}_A\Rightarrow {\left(qgf\right)}^{-1}\left(x\right)=x=\varnothing \in A|qgf\left(x\right)\ne \varnothing \\ 2)\exists qgf\left(x\right)\in qgf{\left(A\right)}_A\Rightarrow x^{\prime }\ne \varnothing \in A|x\ne x^{\prime }\end{array}$ (4)

第一种情况是实地已不复存在的地物，地图上仍保留着消失地物的地图符号。如某处原来是居民地，现实已被夷为平地，但地图上仍保留着居民地符号，这是表示失实，应把失实的地图符号删除。第二种情况是实地的地物已改变性质，但地图符号却没有作相应的改变，从而以使符号与其指代对象不相符。如在原来的居民地处挖成了一个池塘，但地图仍保留着居民地符号，这是明显的性质错误。这种情况下应对地图符号按图式规范作相应的改变，以确保地图符号和指代地物的一一对应性。

3.3. 定义3符号定位超限

设 $p_0\left(x_0,y_0\right)\in qgf\left(x\right)$ 为地图符号 $qgf\left(x\right)$ 的正确定位点，如果实际定位点 $p_1\left(x_1,y_1\right)\in qgf\left(x\right)$，若 $p_1\left(x_1,y_1\right)$ 与 $p_0\left(x_0,y_0\right)$ 之间的距离d满足：

$d\left(p_0,p_1\right)>0.2\text{mm}$ (5)

称为定位超限，对这类地图符号应修改定位以满足 $d\left(p_0,p_1\right)\le 0.2\text{mm}$ 的规范要求。

3.4. 定义4符号与地物定位不符

如果地物与地图符号的定位出现：

$p_1\left(x_1,y_1\right)\in qgf\left(x\right)\in qgf\left(A\right)\Rightarrow p_1\left(x_1,y_1\right)\notin x\in A$ (6)

则称点状地图符号 $qgf\left(x\right)$ 与对应地物x的定位不符。 $p_1\left(x_1,y_1\right)$ 为 $qgf\left(x\right)$ 的定位点。如果

$l_1\in qgf\left(x\right)\in qgf\left(A\right)\Rightarrow l_1\notin x\in A$ (7)

则称线状地图符号 $qgf\left(x\right)$ 与对应地物x的定位不符。 $l_1$ 为 $qgf\left(x\right)$ 的定位线。

4. 地图符号的布尔代数结构及修改地图符号的操作

在地图比例尺限制下的地图平面是有限的空间，在这空间中的地图符号，其中的点状符号是被刻意放大了的非比例符号，线状符号则是横向被夸大了的半依比例符号。而面状符号作为点线符号集的补集则被缩小了。这些地图符号表示的规则及其指代对象的有限性，使任何地图的地图符号都是有限的 [11] [12] [13]。也就是(1)式所包含的地图符号是有限的，设其个数为n。(1)式中显然有下列包含关系：

$\begin{array}{l}qgf{\left(x\right)}^{*}\subset qgf{\left(A\right)}^{*}\subset qgf{\left(A\right)}_A\\ qgf{\left(x\right)}^{*c}\subset qgf{\left(A\right)}^{*c}\subset qgf{\left(A\right)}_A\end{array}$ (8)

设 $qgf{\left(A\right)}_A$ 是基本集合， $T\left(qgf{\left(A\right)}_A\right)$ 是 $qgf{\left(A\right)}_A$ 的幂集，则 $T\left(qgf{\left(A\right)}_A\right)$ 是布尔代数 [14]。对于具有包含关系的布尔代数，可以应用布尔代数算子 $\cup$ 和 $\cap$ 运算和构造相关操作的定义。

5. 修改地图符号的操作定义

地物在时空中的演化是个连续过程，虽然地物的演化对不同性质的地物，不同地区千差万别，但这是不可改变的客观事实。由于地图成图的缺陷不可避免，故地图编制完成时存在一些错误也在所难免。地图错误的修改，实质上是对待改地图实施变换。

5.1. 定义5地图修改

存在 $h:qgf\left(A\right)\to qgf\left(B\right)$，

$\forall qgf{\left(x\right)}^{*c}\in qgf{\left(A\right)}_A\Rightarrow h\left(qgf{\left(x\right)}^{*c}\right)=qgf{\left(x\right)}^{*}\in qgf{\left(A\right)}_B$ (9)

式(9)中的 $qgf{\left(A\right)}_A$ 是包含着错误符号的待改地图。 $qgf{\left(A\right)}_B$ 是经修改消除了错误符号的成图。不同的错误 $qgf{\left(x\right)}^{*c}$ 在变换h下有不同的修改模式。

5.2. 定义6删除符号

存在必须删除的错误符号 $qgf{\left(x\right)}^{*c}\in qgf{\left(A\right)}_A$，则：

$h\left(qgf{\left(x\right)}^{*c}\right)\in qgf{\left(x\right)}^{*c}\cap \varnothing =\varnothing \in qgf{\left(A\right)}_B$ (10)

5.3. 定义7变换性质符号

存在错误符号 $qgf{\left(x\right)}^{*c}\in qgf{\left(A\right)}_A$，但对应的地物为 $x^{\prime }$，于是

$h\left(qgf{\left(x\right)}^{*c}\right)=\left(qgf{\left(x\right)}^{*c}\cap \varnothing \right)\cup qgf{\left(x^{\prime }\right)}^{*}=qgf{\left(x^{\prime }\right)}^{*}\in qgf{\left(A\right)}_B$ (11)

定义2中的第2种情况就用变换性质符号的操作。由于 $gf{\left(x\right)}^{*c}$ 和 $qgf{\left(x^{\prime }\right)}^{*}$ 的任意性，所以本操作可对不同性质的错误符号改变为应予表示的正确地图符号。它是先用错误符号与空集进行交运算再与正确地图符号进行并运算实现。错误符号与∅的交运算发挥了抹去错误符号的“抹布”功能。

5.4. 定义8增补符号

存在 $x\in A\wedge qgf\left(x\right)=\varnothing \in qgf{\left(A\right)}_A|x\ne \varnothing$，则表明地图 $qgf{\left(A\right)}_A$ 上未表示地物 $x\in A$ 的地图符号，这属于定义1中的遗漏，需要在对应的位置上增补x的地图符号 $qgf{\left(x\right)}^{*}$ ：

$h\left(qgf{\left(x\right)}^{*c}\right)=\varnothing \cup qgf{\left(x\right)}^{*}=qgf{\left(x^{\prime }\right)}^{*}\in qgf{\left(A\right)}_B$ (12)

增补符号通过空集 $\varnothing$ 与增补符号 $qgf{\left(x\right)}^{*}$ 的并运算实现。

5.5. 定义9 修正超限符号的定位

正确定位点 $p_0\left(x_0,y_0\right)\notin qgf\left(x\right)\cap p_1\left(x_1,y_1\right)\in qgf\left(x\right)$，若 $d\left(p_0,p_1\right)>0.2\text{mm}$，则称 $p_1\left(x_1,y_1\right)\in qgf(\; x\; )$

定位精度不合规范要求：

$\forall d\left(p_0,p_1\right)>0.2\text{mm}\Rightarrow p_2\left(x_2,y_2\right)\in qgf\left(x\right)s.t.d\left(p_0,p_2\right)\le 0.2\text{mm}$ (13)

则称 $p_2\left(x_2,y_2\right)\in qgf\left(x\right)$ 为符合精度要求的定位，它是对超限定位符号的修正。

5.6. 定义10符号移位

$p_0\left(x_0,y_0\right)\in qgf\left(x\right)$ 为地图符号 $qgf\left(x\right)$ 的正确定位点，而地图符号的实际定位点为 $p_1\left(x_1,y_1\right)\in qgf\left(x\right)\Rightarrow$ 定位错误。这时需要对 $qgf\left(x\right)$ 作移位处理，即实现 $p_1\left(x_1,y_1\right)\in qgf\left(x\right)$ 到 $p_0\left(x_0,y_0\right)\in qgf\left(x\right)$ 的位置变换：

$h\left(p_1\left(x_1,y_1\right)\right)=\left(p_1\left(x_1,y_1\right)\cap \varnothing \cup p_0\left(x_0,y_0\right)\right)=p_0\left(x_0,y_0\right)\in qgf\left(x\right)\in qgf{\left(A\right)}_B$ (14)

对于 $l_1\in qgf\left(x\right)$ 则有：

$h\left(l_1\right)=\left(l_1\cap \varnothing \cup l_0\right)=l_0\in qgf\left(x\right)\in qgf{\left(A\right)}_B$ (15)

6. 地图符号错误的修改算例

地图符号错误的修改，是地图制图技术人员，根据审校检查人员对具体地图审校检查发现的错误，逐一修改，使错误地图符号变换为正确地图符号的过程。所有地图修改，都以错误地图符号集变为空集为目标。由式(1)和(2)可得

$qgf{\left(x\right)}^{*c}=\varnothing \Rightarrow qgf\left(A\right)=qgf{\left(A\right)}^{*}$ (16)

如图1，设 $qgf{\left(A\right)}_A$ 为包含着错误符号集的待改地图， $qgf{\left(A\right)}_B$ 为修改完成的无错漏地图。地图符号错误的修改实质上是从 $qgf{\left(A\right)}_A$ 到 $qgf{\left(A\right)}_B$ 的变换。针对不同的错误性质，对具体的错误地图符号采用不同的变换运算。当且仅当错误地图符号集 $qgf{\left(A\right)}^{*c}=\varnothing$ 时，大功告成。本例中若干错误的修改如下：

1) $a_1\to a_2$，三角点的定位超过误差规定，采用定义9解决，即把定位点由 $p_1\left(x_1,y_1\right)$ 移至 $p_2\left(x_2,y_2\right)$，使其满足 $d\left(p_0,p_2\right)\le 0.2\text{mm}$ 的规范要求。

2) $b_1\to b_2$，从居民地到池塘的变换，地物性质不同，大小有差异，可按定义7的式(10)变换，于是得 $qgf{\left(x^{\prime }\right)}^{*}=qgf{\left(A\right)}_B$ 的结果，图示表明，

$x\ne x^{\prime }\wedge x^{\prime }>x$，即 $b_2>b_1$。

3) $c_1\to c_2$，在空地上开一条连结池塘和河流的沟渠，这是无中生有，是从空集到非空集沟渠的变换，用定义8的式(11)操作完成。

4) $d_1\to d_2$，这是某种性质的地类( $d_1$ 可以是草地、荒地等与 $d_2$ 性质相异的地类)到居民地( $d_2$ 也可是其他异于 $d_1$ 的地类)的变换，用定义7的式(10)操作完成。这里 $x\ne x^{\prime }\wedge x^{\prime }<x$，即 $d_2<d_1$。

5) $f_1\to f_2$，这是类似3)的变换，是无中生有，是在空地上修一段公路与已有的公路连接。是从空集到非空集公路的变换，用定义8的式(11)操作完成。

6) $e_1\to e_2$，原来的一段公路 $e_1$ 移位到了 $e_2$。用定义10的线状地物移位的式(11)操作完成。

本例以6种错误构建 $qgf{\left(A\right)}_A$ 的错误符号集，由于错误设计的任意性，因此，对具体的待改图 $qgf{\left(A\right)}_A$，对错误赋值后都可通过布尔运算，运用相关的修改操作，实现从待改图到完成修改图的变换过程，从而使这地图符号错误修改模型具有普适性。

$qgf{\left(A\right)}_A\to qgf{\left(A\right)}_B$

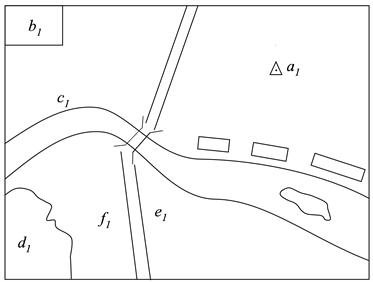
Figure 1. The transformation from a graph awaiting modification to a graph completed with modification

图1. 从待改图到完成修改图的变换

7. 结论

地物在时空中演化的经常性、连续性和编图过程需要时间和流程的矛盾，使某些地物的现实变化未能及时反到地图上，主要表现为地图符号与指代地物不一一对应的错误，从而影响地图的质量。地图审校和检查的目的，就是发现和指出具体图幅错漏。一般情况下，未经审校和检查的地图 $qgf{\left(A\right)}_A$，都包含着正确地图符号集 $qgf{\left(A\right)}^{*}$ 和错误地图符号集 $qgf{\left(A\right)}^{*c}$。 $qgf{\left(A\right)}^{*}$ 和 $qgf{\left(A\right)}^{*c}$ 互为补集。根据未经审校和检查的地图 $qgf{\left(A\right)}_A$ 的幂集是布尔代数系的关系，地图上的错误符号可以通过布尔代数算子 $\cap$， $\cup$ 的运算，实现从错误符号到正确符号的变换。任何待改地图错误符号的有限性，使地图符号的修改必定实现。本文给出的地图符号错误及修改错误的定义，并通过实例，验证了地图符号的修证模型。本文基于编图过程的经验事实，指出了地图符号与其指代地物对应性破损是产生错误的原因，并给出了相关错误及修正错误操作的数学定义，从而使这一问题从经验层面获得了理论上的提升。

基金项目

国家自然科学基金项目(41971416, 42074010, 41871376)；广西科技基地人才专项(桂科AD19110142)。

NOTES

^*第一作者。

^#通讯作者。