1. 引言
当前我国“多煤、贫油、少气”的情况，决定了未来短时间内煤炭作为我国能源主体的地位不会发生改变，但经过几十年的不断开采利用，浅部的煤炭资源将会急剧减少，使得人们不得不向深部地下空间进军。随着开采深度的不断增加，深部巨大的围岩压力以及复杂的地层环境对支护结构的承载力提出了更高的要求。而均质混凝土井壁作为一种煤炭开采中重要的支护结构，如何有效提高井壁的承载能力引起了许多学者的关注。目前提高井壁承载能力的解决方法主要有提高混凝土材料强度、增加井壁厚度以及使用特殊结构三种方法。针对提高材料强度来提高立井井壁的承载能力的方法，姚直书等 [1] 学者曾提出混凝土强度提高10 MPa，则井壁承载力将提高约13.8%。而对于增加井壁厚度提高井壁的承载能力的方法，Zhang N.等 [2] 学者曾提出对于延伸至1000 m深的竖井，衬砌厚度增加10 mm，钢筋混凝土将增加1%的总成本，而普通混凝土将增加0.25%的总成本。可见，此种方法会增加施工成本。同时，传统均质井壁在承受外压作用下，井壁内侧会出现环向应力集中的现象，但井壁外侧混凝土却得不到有效发挥，因此上述两种方法提高井壁承载力的范围十分有限，并且将会造成材料的浪费。因此，较多的国内外学者将功能梯度材料引入了立井井壁。
功能梯度材料(FGM)是一种组成和性能在空间上呈连续变化的新型复合材料，最早是由日本科学家 [3] 提出，用于解决航空航天领域中极端环境下材料的隔热问题。为了应对深部地下复杂的情况，一些学者提出利用功能梯度材料的材料性能在空间连续变化的特性来缓解井壁结构中应力集中现象，达到“柔性让压”的效果，从而充分发挥井壁外侧混凝土的承载能力，提高井壁的极限承载力。现有的功能梯度立井井壁的研究，大多是对功能梯度圆筒沿半径方向的弹性模量进行了各种函数假设 [4] [5] [6] [7]，从而研究功能梯度立井井壁的力学特性。但在实际工程中要使材料弹性模量实现沿某一方向的连续变化十分困难。因此，不少学者则将层合模型引入，即将立井井壁分为多层同轴圆筒结构分层赋予不同材料，从而使材料弹性模量的达到近似连续变化。其中张宁 [8] [9] 设计了一种由多层同轴不同弹性模量的混凝土层制成的功能梯度立井井壁，但却没有完善的理论体系去指导实际工程设计。因此，许冲 [10] 借助ABAQUS软件对功能井壁受力变形规律进行了数值模拟，并基于其理论研究设计了一款功能梯度井壁结构的设计软件为工程设计提供了依据。此外，深部地下地质环境复杂，井壁不仅要能抵抗住强大的压力，而且要满足多种功能特性。基于此李德春 [11] 等人提出一种新型功能梯度井壁结构，使得井壁具有了抗渗、抗水压、抗腐蚀、抗火等多种功能特性。上述对于功能梯度井壁的研究，均是基于井壁外侧所受的是均匀荷载的理想情况。针对这一不足，李德春 [12] 等人又对非均布荷载侧压力情况提出了一种弹性模量沿环向改变的功能梯度立井井壁。
目前基于层合模型的功能梯度圆筒的具体分层数选取以及各分层中混凝土的具体弹性模量大小的选取带来的影响却鲜有研究，导致无法将功能梯度井壁在实际工程中进行推广运用。本文基于上述的层合模型，将功能梯度立井井壁划分为多层同轴圆筒，并使用ABAQUS进行有限元仿真，探究了在立井井壁分层数不变的情况下，取层间弹性模量差值在1 Gpa到10 Gpa之间引起的多层井壁圆筒的应力变化，并对比了6、10、15层数下立井井壁各层间的最合适弹性模量梯度差值的改变情况，对于指导功能梯度井壁在实际工程中的设计施工具有重要意义。
2. 有限元模型建立
本文将多层同轴的功能梯度立井井壁的混凝土弹性模量E假设为一个沿半径变化的线性函数，其泊松比μ为常数，通过ABAQUS分别建3个立井层数n为6、10、15层的多层功能梯度立井井壁结构有限元模型，每层圆筒中的弹性模量相同，各层间弹性模量差值相等，整体结构上弹性模量沿半径方向上满足内小外大的线性分布。
计算模型参数如表1所示。
Table 1. Calculation model parameters
表1. 计算模型参数
使用ABAQUS进行数值模拟计算，采用二维平面模型，由于井壁为轴对称结构，取1/4结构研究，井壁截面为对称边界，采用定向支座，在井壁外侧施加荷载，层数n = 10时计算模型示意图如图1所示。所有计算模型的网格划分形式相同，层数n = 6时划分为2700个单元，n = 10时划分为2406个单元，n = 15
Figure 1. Schematic diagram of calculation model when n = 10
图1. n = 10时计算模型示意图
时划分为2400个单元，单元类型为CPE4R，n = 10时网格划分图如图2所示。
Figure 2. Grid division diagram when n = 10
图2. n = 10时网格划分图
3. 仿真结果分析
3.1. n = 6时Mises应力云图分析
除了一些众所周知的英文缩写，如IP、CPU、FDA，所有的英文缩写在文中第一次出现时都应该给出其全称。文章标题中尽量避免使用生僻的英文缩写。
立井井壁分为6层时，层间弹性模量差值取1 Gpa到10 Gpa之间情况下，计算得到的应力云图如图3所示，不同的层间弹性模量差值计算得到的最大应力、最小应力如表2所示。
通过应力云图、最大应力及最小应力，我们可以看出最大应力伴随着层间弹性模量差值由0 GPa和10 GPa分别向5.25 GPa处减小，Mises应力分布由0 GPa的内侧应力大外侧应力小逐渐变化到5.25 GPa的相对均匀(即有效缓解了井壁内侧的应力集中现象)，再到10 GPa的内侧应力小外侧应力大。
(a) 层间弹性模量差值为1 GPa 
(b) 层间弹性模量差值为10 GPa 
(c) 层间弹性模量差值为5 GPa 
(d) 层间弹性模量差值为6 GPa
Figure 3. Mises stress cloud at n = 6
图3. n = 6时Mises应力云图
Table 2. Maximum stress and minimum stress calculated with the change of elastic modulus difference between layers when n = 6
表2. n = 6时随层间弹性模量差值变化计算得到的最大应力和最小应力
3.2. n = 10时Mises应力云图分析
立井井壁分为10层时，层间弹性模量差值取1 Gpa到10 Gpa之间情况下，计算得到的应力云图如图4所示，不同层间弹性模量差值计算得到的最大应力、最小应力如表3所示。
通过应力云图、最大应力及最小应力，我们可以看出最大应力伴随着层间弹性模量差值由0 GPa和10 GPa分别向3.25 GPa处减小，Mises应力分布由0 GPa的内侧应力大外侧应力小，逐渐变化到3.25 GPa的相对均匀(即有效缓解了井壁内侧的应力集中现象)，再到10 GPa的内侧应力小外侧应力大。
(a) 层间弹性模量差值为1 GPa 
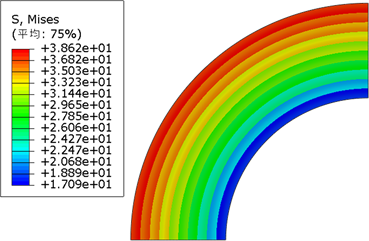(b) 层间弹性模量差值为10 GPa 
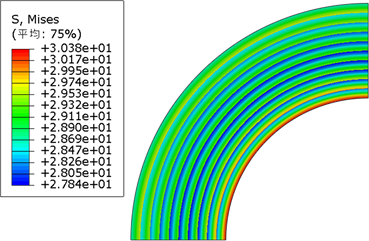(c) 层间弹性模量差值为3 GPa 
(d) 层间弹性模量差值为4 GPa
Figure 4. Mises stress cloud at n = 10
图4. n = 10时Mises应力云图
Table 3. Maximum stress and minimum stress calculated with the change of elastic modulus difference between layers when n = 6
表3. n = 10时随层间弹性模量差值计算得到的最大应力和最小应力
3.3. n = 15时Mises应力云图分析
立井井壁分为10层时，层间弹性模量差值取1 Gpa到10 Gpa之间情况下，计算得到的应力云图如图5所示，不同层间弹性模量差值计算得到的最大应力、最小应力如表4所示。
通过应力云图、最大应力及最小应力，我们可以看出最大应力伴随着变化值由0 GPa和10 GPa分别向2.00 GPa处减小，Mises应力分布由0 GPa的内侧应力大外侧应力小，逐渐变化到2.00 GPa的相对均匀(即有效缓解了井壁内侧的应力集中现象)，再到10 GPa的内侧应力小外侧应力大。
(a) 层间弹性模量差值为1 GPa 
(b) 层间弹性模量差值为10 GPa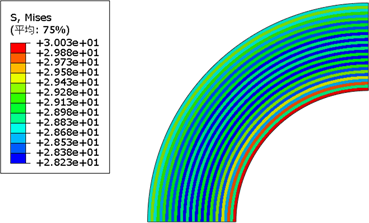 
(c)层间弹性模量差值为2 GPa 
(d) 层间弹性模量差值为3 GPa
Figure 5. Mises stress cloud at n = 15
图5. n = 15时Mises应力云图
Table 4. Maximum stress and minimum stress calculated with the change of elastic modulus difference between layers when n = 15
表4. n = 15时随层间弹性模量差值计算得到的最大应力和最小应力
基于上述三种不同层数的Mises应力云图分析中我们得出，不同层数下对应的立井井壁中的应力会随着层间弹性模量差值的变化相应发生改变，且改变的趋势是一致的，都是随着层间弹性模量差值的不断增大，井壁内部的应力从开始的内侧附近应力大外侧应力小，到整体应力逐渐分布的越来越均匀(即有效缓解了井壁内侧的应力集中现象)，最后转变为内侧应力小而外侧应力大的状态。不难发现，不同层数均对应一个最合适的层间弹性模量差值，即为Mises应力状态在井壁结构内部分布为相对均匀时对应的层间弹性模量差值，并且这个数值随着层数的增加而减小，即层数15的最适层间弹性模量差值 < 层数10的最适层间弹性模量差值 < 层数6的最适层间弹性模量差值。
4. 仿真结果原因分析
为了解释上述井壁结构内部Mises应力出现的随层间弹性模量差值改变而逐渐均匀化的现象(即有效缓解了井壁内侧的应力集中现象)，我们通过对n = 10的多层功能井壁结构的径向和环向的应力进行分析，沿井壁半径方向选取一条参考路径，方向为由井壁内侧至井壁外侧，将环向应力、径向应力等计算结果整理如表5所示。同时我们还将n = 10时Mises应力、径向应力、环向应力与圆筒半径的关系进行表示，如图6所示。
从表5可以得出，当划分层数为10时，径向应力沿半径由内到外逐渐增大，最大值存在于井筒外边界，由于外侧均压的存在，其值为15 MPa，最小值为存在于井筒内边界，其值随着层间弹性模量差值增大而减小。而环向应力在层间弹性模量差值小于最合适层间弹性模量差值时，应力大小沿半径由内到外逐渐减小；在层间弹性模量差值大于最合适层间弹性模量差值时，应力大小沿半径由内到外逐渐增大。井壁内部各点的环向应力和径向应力相比，环向应力远大于径向应力，并且层间弹性模量差值的改变，引起的各点径向应力变化很小(最大、最小应力变化量都未超过0.5 Mpa)，但对各点环向应力的影响却十分明显，即环向应力占据影响Mises合应力大小的主导地位，所以环向应力随着层间弹性模量差值的增大，从最初的环向应力内侧大外侧小，到相对均匀，再到内侧小外侧大，从而引起环向应力和径向应力合成的Mises应力发生类似上述现象的变化趋势。
此外，对于井壁内部应力相对均匀的状态的最适层间弹性模量差值随着层数的增加而减小的现象可以做出如下合理解释。本文是假设井壁弹性模量沿径向线性变化(即E(r) = Ar + B)，根据吕爱钟和张路青 [13] 提出的采用反分析法可以反演推导出满足预定应力状态条件下，功能梯度井壁沿径向方向弹性模量的最优变化函数的结论，可以得知井壁一定会存在一种沿径向最优的弹性模量线性变化函数，使得井壁内部应力分布达到最均匀的状态。
其中上文中得到的最适层间弹性模量差值对应为最优线性变化函数的参数A和Δr (各层厚度)的乘积A*Δr，因此随着划分层数的增加，各层的厚度Δr也越来越小，整体上拟合弹性模量的变化函数也就越来越精确，井壁弹性模量沿半径方向的变化也变得更加连续，乘积A*Δr也对应变小，所以层间的弹性模量差值也会逐渐减小。与此同时，功能梯度井壁的“柔性让压”特性却越来越显著，从而有限缓解内侧应力集中的现象。即层数15的最适层间弹性模量差值 < 层数10的最适层间弹性模量差值 < 层数6的最适层间弹性模量差值。
Table 5. Changes of Mises stress, radial stress and circumferential stress calculated with the difference of elastic modulus between layers at n = 10
表5. n = 10时随层间弹性模量差值变化计算得到的Mises应力、径向应力、环向应力的变化情况
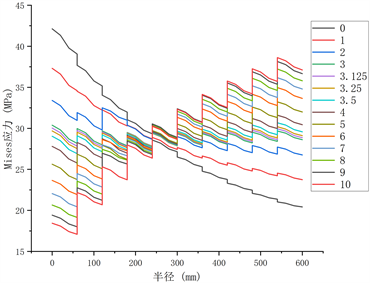(a) Mises应力与圆筒半径关系 
(b) 径向应力与圆筒半径关系 
(c) 环向应力与圆筒半径关系
Figure 6. Relationship between Mises stress, radial stress, annular stress and cylinder radius at n = 10
图6. n = 10时Mises应力、径向应力、环向应力与圆筒半径的关系
5. 结论
1、各种层数均对应一个最合适的层间弹性模量差值，使得功能梯度立井井壁Mises应力达到相对均匀(即有效缓解了井壁内侧的应力集中现象)，井壁内部的最大应力达到最小。
2、最合适层间弹性模量差值随着层数增加而减小，即层数15的最适层间弹性模量差值 < 层数10的最适层间弹性模量差值 < 层数6的最适层间弹性模量差值。
3、井壁内部各点环向应力均大于径向应力，并且随着层间弹性模量差值的增大，各点环向应力的变化十分显著，但径向应力变化很小，即环向应力占据影响Mises应力的主导地位，决定了两者合成的Mises应力的变化趋势。即环向应力随着层间弹性模量差值的增大，从初的应力内侧大外侧小，到相对均匀，再到内侧小外侧大，从而引起环向应力和径向应力合成的Mises应力发生与环向应力相同的变化趋势。
4、在实际工程运用中，可利用上述得出的各分层数下最合适层间弹性模量差值来设计功能梯度立井井壁，确定各层混凝土的弹性模量，从而配置符合条件的混凝土。并且设计的井壁分层数越多，需要配置的混凝土的弹性模量整体上也就越低，可以在达到缓解井壁内侧应力集中的同时达到降低成本的目的，但井壁的分层数也不应过多，否则会导致各层厚度过小，不便于施工中浇筑混凝土。