基于稀疏约束和对偶图正则化的受限概念分解算法及在数据表示中的应用

Constrained Concept Factorization Based on Sparseness Constraints and Dual Graph Regularization for Data Representation

摘要: 概念分解算法(CF)是一种经典的数据表达方式，已经被广泛使用于机器视觉、模式识别等领域。基本的CF方法是一种无监督的学习算法，无法利用数据中存在的先验知识，没有考虑数据空间流形和特征空间流形的几何结构信息，同时分解结果也不具有稀疏性。为了解决以上缺陷，本文提出了一种基于稀疏约束和对偶图正则化的受限概念分解算法(DCCFS)。该算法通过保持样本数据空间和特征空间中内蕴的几何结构信息不变，使得算法可以更加有效提取数据的特征，增强了算法的数据表达能力；利用数据中天然存在的类别性息，增强算法的鉴别能力；添加LP平滑范数提高了算法的稀疏性，使得分解结果更加准确、平滑。在COIL20图像数据集、PIE人脸数据集以及TDT2文本数据集上的聚类实验证明本文提出的DCCFS的聚类性能优于其他同类算法。

Abstract: Concept decomposition algorithm (CF) is a classical data representation that has been widely used in machine vision, pattern recognition and other fields. In response to the fact that the basic CF method is an unsupervised learning algorithm that does not consider the geometric structure information and the class information of the samples present in the data space and feature space, and also does not take into account the sparsity of the decomposition results, this paper proposes a novel method named constrained concept factorization based on sparseness constraints and dual graph regularization for data representation (DCCFS) to overcome the above defects. This method constructs the geometric structure information in the sample data space and feature space unchanged, which extracts the features of the data more effectively and enhances the data expression ability of the algorithm; by using the natural label information in the data to enhance the identification ability of the algorithm; DCCFS adds the smooth sparse constraint to make the matrix factorization process more stable, smooth, which makes sure that the results are more accurate. The experimental results on COIL20 image dataset, PIE face dataset and TDT2 text dataset show that the DCCFS method can provide better representation for high-dimensional data and effectively improve the clustering performance.

1. 引言

低秩矩阵分解是科学计算、数据挖掘和计算机视觉中最有用的工具之一。如何从高维数据中探索有效的数据低维表示方法至今仍是一个基础课题 [1] [2] [3]。近些年来，低维数据表示技术受到了研究人员的关注，并被广泛应用于数据挖掘、计算机视觉和信息检索等领域。常用的低维数据表示技术是矩阵分解，其目的是获得两个或多个低维矩阵，并使其乘积尽可能接近原始数据矩阵。使用矩阵分解技术可以保留原始高维图像的特征信息、挖掘出图像蕴含的现在的语义结构，有利于机器学习、计算机视觉等领域的进一步发展。一些典型的矩阵分解算法有主成分分析(principal component analysis, PCA) [4]、矢量量化(vector quantization, VQ) [5]、奇异值分解(singular value decomposition, SVD) [6]、线性判别分析(Linear discriminant analysis, LDA) [7]、非负矩阵分解(Non-negative matrix factorization, NMF) [8]、概念分解(Concept Factorization, CF) [9] 以及与深度学习技术相结合的一些列矩阵分解方法 [10] [11]。在以上矩阵分解方法中，非负矩阵分解(NMF)和概念分解(CF)作为两个有效的数据降维工具，受到了研究人员的青睐，已被广泛应用于数据分析的任务中。

假设存在一个高维矩阵，NMF的分解目标是将该高维矩阵转化为两个低维矩阵的乘积，使用两个低维矩阵(基矩阵和系数矩阵)的乘积来近似原始高维矩阵。同时，NMF还有一个最基本的附加条件，即两个低维矩阵中的所有的元素都是非负，只进行加法运算而不进行减法运算，因此，NMF是一个整体基于部分的图像表示方法，在心理和生理上具有较强的解释性。该附加条件使得NMF在处理图像、文档等聚类任务时优于PCA、SVD、LDA等传统数据降维算法。但是，NMF无法处理数据中由噪声造成的含有负元素的数据矩阵，这使得NMF在处理实际问题时具有局限性。为了解决此类问题，Xu等提出概念分解算法(CF)用于文本聚类以及图像表达。CF不仅可以解决由噪声引起的矩阵中含负元素问题，无需考虑正负，还可以处理高维数据，并可以很容易的对其进行核化，保留了NMF所有的优点。CF算法的核心思想是建立一个聚类模型，其中每个聚类由数据点的线性组合表示，每个数据点由聚类中心的线性组合表示。

Cai等在流形学习的基础上，利用流形学习的思想对基本的NMF和CF的模型中进行改进，提出了GNMF [12] 和LCCF [13]。主要工作是对基本的NMF和CF模型中施加图正则化以保证了数据间的几何流形结构不变。Liu等人 [14] 为了数据间存在的标签信息，将基本的CF模型改进为一种半监督的学习算法，提出了一种基于局部受限的概念分解(LC-CF)方法，LC-CF对基本的CF模型施加局部正则化约束，通过提取与部分已知标签信息一致的图像信息，并使具有相同标签的数据点在低维空间中被映射至同一点上。Tang [15] 在考虑数据流形的基础上，还考虑了特征流形，提出了ODGNMF算法，扩展了GNMF的学习能力。但是，以上的均从数据的先验知识方面对NMF或CF加以改进，没有考虑到算法的稀疏性。研究表明 [16] [17] [18]，对算法施加稀疏约束，使得算法可以学习数据的稀疏表示，有效提高算法的鲁棒性，进一步提高分解结果稳定性、平滑性，使得算法具有更高的学习效率。

因此，本文提出了一种新的方法，称为基于稀疏约束和对偶图正则化的受限概念分解算法(Constrained Concept Factorization Based on Sparseness Constraints and Dual graph regularization, DCCFS)用于数据表示。DCCFS不仅利用流形学习的思想考虑了数据空间流形和特征空间流形上的内部几何结构，而且还利用了无参数的标记样本的标签信息，将基本的无监督CF算法扩展为半监督算法，增强了算法的鉴别能力，最后，加入了 $L_P$ 平滑约束以考虑算法的稀疏性。为了得到该算法的迭代式，我们提出了一种基于乘法更新算法的高效优化算法来解决所提出的模型。在几个公共数据集上的实验表明，我们提出的DCCFS方法优于相关的最先进方法。

2. 相关工作

2.1. 非负矩阵分解(NMF)

假设有一原始非负矩阵 $X=\left[x_{ij}\right]\in {ℝ}^{M\times N}$ 被分解成两个低维矩阵，分别为 $U=\left[u_{ik}\right]\in {ℝ}^{M\times K}$ ， $V=\left[v_{jk}\right]\in {ℝ}^{N\times K}$ ，两个低维矩阵得乘积无限逼近原始矩阵，则NMF的表达式如下：

$\begin{array}{l}{O}_{NMF}={\displaystyle \underset{i=1}{\overset{N}{\sum }}{\displaystyle \underset{j=1}{\overset{M}{\sum }}{\left(X_{ij}-{\left(U{V}^{\text{T}}\right)}_{ij}\right)}^2}}={\Vert X-U{V}^{\text{T}}\Vert }_F^2\\ \text{s}\text{.t}\text{.}U\ge 0,V\ge 0\end{array}$ (2.1)

其中 ${\Vert \cdot \Vert }_F$ 代表范德蒙范数， $K\ll \min \left(M,N\right)$。M表示维度，N表示样本总数，U表示基矩阵，V表示系数矩阵也称作权重矩阵。使用交替乘性更新算法可得到NMF的迭代规则如下：

$u_{ik}\leftarrow u_{ij}\frac{{\left(XV\right)}_{ij}}{{\left(U{V}^{\text{T}}V\right)}_{ij}}$ (2.2)

$v_{jk}\leftarrow v_{ij}\frac{{\left(X^{\text{T}}U\right)}_{ij}}{{\left(V{U}^{\text{T}}U\right)}_{ij}}$ (2.3)

由于 $K\ll \min \left(M,N\right)$ ，此时基矩阵U和系数矩阵V的秩远小于原始矩阵X的秩，此时便实现了由高维矩阵到低维矩阵的降维。

2.2. 概念分解(CF)

假设有一矩阵 $X=\left[x_{ij}\right]\in {ℝ}^{M\times N}$ ，CF的任务是找到基矩阵 $V=\left[v_{ij}\right]\in {ℝ}^{N\times K}$ ，系数矩阵 $W=\left[w_{ij}\right]\in {ℝ}^{N\times K}$。 $v_j$ 称为基向量，是数据样本的非线性组合， $v_j$ 可表示如下：

$v_j={\displaystyle \underset{i}{\sum }{W}_{ij}{X}_i}\left(W_i{}_j\ge 0\right)$ (2.4)

其中 $W=\left[w_{ij}\right]\in {ℝ}^{N\times K}$。因此CF的目的是找到低秩矩阵W和V，使得W和V的乘积满足以下关系：

$X\approx XW{V}^{\text{T}}$ (2.5)

使用Frobenius范数，CF的目标函数可表示为：

$\begin{array}{l}{O}_{CF}={\Vert X-XW{V}^{\text{T}}\Vert }_F^2\\ \text{s}\text{.t}.W>0,V>0\end{array}$ (2.6)

使用交替乘性更新算法求解 CF 的目标函数，CF的更新规则可以表示为：

$W_{ij}^{t\text{+1}}\leftarrow W_{ij}^t\frac{{\left(KV\right)}_{jk}}{{\left(KW{V}^{\text{T}}V\right)}_{jk}}$ (2.7)

$V_{ij}^{t\text{+1}}\leftarrow V_{ij}^t\frac{{\left(KW\right)}_{ij}}{{\left(V{W}^{\text{T}}KW\right)}_{ij}}$ (2.8)

其中， $K=X^{\text{T}}X$。

3. 基于稀疏约束和对偶图正则化的受限概念分解算法(DCCFS)

3.1. 引言

流形学习 [19] 表明，数据中存在有潜在的低维子流形，称之为数据流形。数据点间的几何拓扑结构都会在数据流形上显示。研究表明 [20]，数据间的特征同样也分布在一个低维子流形上，可将之称为特征流形 [19]，因此在对数据降维时，需要同时考虑到原始数据空间中存在的数据流性几何结构信息以及特征空间上的特征流形几何结构信息。通过构造数据图和特征图模型，刻画数据流形和特征流形的几何结构，可以保证数据在低维空间中仍然保持了高维空间中几何结构信息，保证算法学习的质量，因此该方法也被称为构造对偶图。

但是，该方法没有考虑到数据中潜在的类别信息。现实中的数据含有潜在的类别信息，人为的对这些类别信息添加标签，可以使之转化为标记信息。有效的利用样本中存在的标记信息将会提高算法的精度与数据表达能力，因此，在流形学习的基础上结合标记信息，将基本的CF算法从无监督转化为半监督是很有必要的。最后，考虑到算法的稀疏性，使用 $L_P$ 平滑约束可以滤除无用特征信息、防止过拟合、得到更加稀疏的特征向量，算法得到一个准确、平滑的解。

DCCFS通过 $L_P$ 平滑约束提高算法的稀疏性，构造偶图得到样本数据空间和特征空间的流形结构信息，提高了算法的数据的挖掘能力，最后将标签信息转化为硬约束，揭示隐藏语义，提高算法的学习能力。

3.2. 构造对偶图正则项

研究表明，样本的数据不仅存在于非线性的低维流形上(数据流形)，数据的特征也存在于非线性流形上，称为特征流形。因此，可以构造数据流形和特征流形的最邻近图的几何结构来有效建模数据流形和特征流形的几何结构。

假设存在一个k最近邻数据图，其顶点对应于 $\left\{X_1,\cdots ,X_N\right\}$ ，使用0~1加权方案来构造k最近邻图，并定义数据权重矩阵如下：

$S_{ij}^V=\{\begin{array}{l}1,\text{if}{x}_j\in N_p\left(x_i\right);\hfill \\ 0,\text{otherwise}\hfill \end{array}i,j=1,\cdots ,n$ (3.1)

其中， $N_p\left(x_i\right)$ 是 $x_i$ 的p邻近集，数据图的拉普拉斯矩阵定义为：

$L^V=D^V-S^V$ (3.2)

其中， $D^V$ 是对角线矩阵， $D_{ii}^V={\displaystyle {\sum }_j{S}_{ij}^V}$。

假设存在矩阵V为待求的低维数据表示， $V=\left[v_1^{\text{T}},v_2^{\text{T}},\cdots ,v_n^{\text{T}}\right]\in R^{n\times k}$ ，通过前文定义的 $S^V$ ，可以使用 ${\Re }_1$ 衡量数据在低维表示的空间中的光滑程度，定义如下：

$\begin{array}{c}{\Re }_1=\frac{1}{2}{\displaystyle \underset{i,j=1}{\overset{n}{\sum }}{\Vert v_i-v_j\Vert }^2{S}_{ij}^V}\\ ={\displaystyle \underset{i=1}{\overset{n}{\sum }}{v}_i{v}_i^{\text{T}}{D}_{ii}^V-}{\displaystyle \underset{i,j=1}{\overset{n}{\sum }}{v}_i{v}_j^{\text{T}}{S}_{ij}^V}\\ =Tr\left(V^{\text{T}}{D}^{V}V\right)-Tr\left(V^{\text{T}}{S}^{V}V\right)\\ =Tr\left(V^{\text{T}}{L}_{V}V\right)\end{array}$ (3.3)

其中， $Tr(\cdot )$ 表示矩阵的迹。为了尽可能使得数据集在低维空间中保持光滑，需要最小化 ${\Re }_1$ ，即如果两个数据点 $x_i$ 和 $x_j$ 距离较近，则两点在低维空间中对应的点 $v_i$ 和 $v_j$ 距离也是彼此接近的。此时通过最小化 ${\Re }_1$ ，保证高维空间中映射到低维空间中的点保持光滑。因此，式(3.3)也被称为数据图的拉普拉斯正则项。

同样的方法，构造一个p最近邻点特征图，其顶点对应于 $\left\{x_1^{\text{T}},\cdots ,x_m^{\text{T}}\right\}$ ，然后使用0~1加权方案来构造特征矩阵，并定义数据权重矩阵如下：

$S_{ij}^U=\{\begin{array}{l}1,\text{if}{x}_j^{\text{T}}\in M_p\left(x_i^{\text{T}}\right);\hfill \\ 0,\text{otherwise}\hfill \end{array}i,j=1,\cdots ,m$ (3.4)

其中， $M_p\left(x_i^{\text{T}}\right)$ 是 $x_i^{\text{T}}$ 的p邻近集，特征图的拉普拉斯矩阵定义为：

$L_U=D^U-S^U$ (3.5)

其中， $D^U$ 是对角矩阵， $D_{ii}^U={\displaystyle {\sum }_j{S}_{ij}^U}$。

令 $U=\left[u_1^{\text{T}},u_2^{\text{T}},\cdots ,u_m^{\text{T}}\right]\in R^{m\times k}$ 为待求的低维数据表示，使用 ${\Re }_2$ 衡量数据在低维表示的空间中的光滑程度，定义如下：

$\begin{array}{c}{\Re }_2=\frac{1}{2}{\displaystyle \underset{i,j=1}{\overset{m}{\sum }}{\Vert u_i-u_j\Vert }^2{S}_{ij}^U}\\ ={\displaystyle \underset{i=1}{\overset{m}{\sum }}{u}_i{u}_i^{\text{T}}{D}_{ii}^U}-{\displaystyle \underset{i,j=1}{\overset{m}{\sum }}{u}_i{u}_j^{\text{T}}{S}_{ij}^U}\\ =Tr\left(U^{\text{T}}{D}^{U}U\right)-Tr\left(U^{\text{T}}{S}^{U}U\right)\\ =Tr\left(U^{\text{T}}{L}_{U}U\right)\end{array}$ (3.6)

3.3. 构造受限矩阵

CF是一种无监督学习算法，没有考虑样本的类别信息，不能直接应用于标签信息可用的情况。相关研究表明将数据中的标签信息转化为硬约束可以有效提高算法的鉴别能力以及算法的聚类性能。假设数据集 ${\left\{x_i\right\}}_{i=1}^n$ 中前l个样本已标记，剩余 $n-l$ 个为未标记样本，数据集X可被划为C个集簇。前l个数据点都被标记为这些集簇中的一个。由此建立个指示矩阵 $M_{l\times c}$ ，假设x被标记为第j个集簇，则 $m_{ij}=1$ 否则 $m_{ij}=0$ ，此时矩阵A如下：

$A=\left(\begin{array}{cc}{M}_{l\times c}& 0\\ 0& I_{n-l}\end{array}\right)$ (3.7)

其中I是单位矩阵。为了充分利用标签信息，通过引入辅助矩阵Z施加标签约束。系数矩阵可以重写如下：

$V=AZ$ (3.8)

3.4. DCCFS目标函数

为了充分利用数据的先验知识，如数据流形和特征流形的几何结构信息、标签信息以及算法的稀疏性，本文提出了一种新的图像表示方法DCCFS。DCCFS尽可能地考虑了更多的先验知识，因此与传统的CF方法相比具有更强的表示能力。拟议DCCFS方法的目标函数如下所示：

$O_F={\Vert X-XW{Z}^{\text{T}}{A}^{\text{T}}\Vert }_F^2+\lambda Tr\left(Z^{\text{T}}{A}^{\text{T}}{L}_{Z}AZ\right)+\alpha Tr\left(W^{\text{T}}{L}_{W}W\right)+2\mu {\Vert W\Vert }^p$ (3.9)

其中 $L_Z=L_V=D^Z-S^Z$ ， $L_W=X^{\text{T}}{L}_{U}X=X^{\text{T}}\left(D^U-S^U\right)X=D^W-S^W$ ，A代表标签约束矩阵，而Z表示一个辅助矩阵，系数矩阵 $V=AZ$。 $\lambda \ge 0$ 、 $\alpha \ge 0$ 、 $\mu \ge 0$ ，三者是正则化参数，均是用来平衡重建误差。P的取值在1和2间， $L_V$ 和 $L_U$ 分别是数据图和特征图的拉普拉斯矩阵。

3.5. DCCFS目标函数求解

很明显，DCCFS的目标函数是非凸的，因此无法找到全局最优解，使用乘法迭代算法可解决此问题，具体做法为固定一个变量的情况下，对另一个变量的目标进行优化。另外，根据矩阵迹的特点， $Tr\left(A^{\text{T}}\right)=Tr\left(A\right)$ ， $Tr\left(AB\right)=Tr\left(BA\right)$ ，此时可以实现DCCF模型的局部最小值。那么，公式(3.9)可以进一步改写如下。

$\begin{array}{c}{O}_F={\Vert X-XW{Z}^{\text{T}}{A}^{\text{T}}\Vert }_F^2+\lambda Tr\left(Z^{\text{T}}{A}^{\text{T}}{L}_{Z}AZ\right)+\alpha Tr\left(W^{\text{T}}{L}_{W}W\right)+2\mu {\Vert W\Vert }^p\\ =Tr\left({\left(X-XW{Z}^{\text{T}}{A}^{\text{T}}\right)}^{\text{T}}\left(X-W{Z}^{\text{T}}{A}^{\text{T}}\right)\right)\\ +\lambda Tr\left(Z^{\text{T}}{A}^{\text{T}}{L}_{Z}AZ\right)+\alpha Tr\left(W^{\text{T}}{L}_{W}W\right)+2\mu {\Vert W\Vert }^p\\ =Tr\left(K\right)-2Tr\left(W{T}^{\text{T}}KAZ\right)+Tr\left(W^{\text{T}}KW{Z}^{\text{T}}{A}^{\text{T}}AZ\right)\\ +\lambda Tr\left(Z^{\text{T}}{A}^{\text{T}}{L}_{Z}AZ\right)+\alpha Tr\left(W^{\text{T}}{L}_{W}W\right)+2\mu {\Vert W\Vert }^p\end{array}$ (3.10)

利用乘性迭代算法，简化式(1.18)。由于 $U\ge 0,V\ge 0$ ，假设 $\Psi =\left[{\psi }_{ik}\right]$ 和 $\varphi =\left[{\phi }_{jk}\right]$ 分别式关于U和Z的拉格朗日乘数，因此，式(3.10)的拉格朗日函数L可写成如下：

$L=O_F+Tr\left(\psi W^{\text{T}}\right)+Tr\left(\phi Z^{\text{T}}\right)$ (3.11)

L对U和Z的偏导数如下所示：

$\frac{\partial \mathcal{l}}{\partial W}=-2KAZ+2KW{Z}^{\text{T}}{A}^{\text{T}}AZ+2\alpha L_{W}W+\psi +2\mu P{W}^{P-1}$ (3.12)

$\frac{\partial \mathcal{l}}{\partial Z}=-2A^{\text{T}}KW+2A^{\text{T}}AZ{W}^{\text{T}}KW+2\lambda A^{\text{T}}{L}_{Z}AZ+\Phi$ (3.13)

根据KKT条件， $\phi U=0$ ， $\varphi V=0$ ，等式(3.12)和(3.13)可被改写为：

$w_{ij}^{t+1}\leftarrow w_{ij}^t\frac{{\left(KAZ+\alpha S^{W}W\right)}_{ij}}{{\left(KW{Z}^{\text{T}}{A}^{\text{T}}AZ+\alpha D^{W}W+\mu P{W}^{P-1}\right)}_{ij}}$ (3.14)

$z_{ij}^{t+1}\leftarrow z_{ij}^t\frac{{\left(A^{\text{T}}KW+\lambda A^{\text{T}}{S}^{Z}AZ\right)}_{ij}}{{\left(A^{\text{T}}AZ{W}^{\text{T}}KW+\lambda A^{\text{T}}DAZ\right)}_{ij}}$ (3.15)

3.6. DCCFS算法具体步骤

本文提出的DCCFS算法迭代步骤如下表1所示：

Table 1. Iterative steps of DCCFS algorithm

表1. DCCFS算法迭代步骤

4. 数值实验

在本节中，为了评估所提出的DCCFS模型的有效性，我们在PIE、COIL20、TDT2三个公共数据集上进行了数值的实验。我们将我们提出的方法与其他方法包括KM、NMF、GNMF、CF、LCCF、GCF和DCCFS进行比较。在本实验中，将使用准确度(AC)和归一化互信息(NMI)作为所有方法的聚类评估指标。

4.1. 数据集介绍

本实验将在人脸数据集PIE、物体数据集COIL20以及文本数据集TDT2上进行。在本实验中，我们从PIE数据集中选取不同对象的11,554幅图像，图像分辨率为32 × 32，每张图片都是在不同的姿势和光照变化条件下收集的；COIL20数据集这包含了20种不同物体的图像(如具鸭、杯子等)，每个物体360度，每5度拍摄一张图片，因此每个物体拥有72张图片，20个不同的物体则拥有1440张图片，图像大小为32 × 32；TDT2文本数据集共包含了56类，10,021个文档，在该数据集上本实验选取了每类数目大于10的样本用于聚类实验。

4.2. 实验介绍

在本实验中，我们从PIE数据集、COIL20数据集、TDT2数据集中随机选择K类样本进行实验，K的取值均为2到10。实验将所有挑选出来的实验图像混合放入集合X中，对于每个K值，所有方法运行20次取平均值，从而获取每种方法的准确度(AC)、归一化互信息(NMI)。实验结果如下表2~4所示：

Table 2. Clustering experimental results on PIE database

表2. PIE数据库上的聚类实验结果

Table 3. Clustering experimental results on COIL20 database

表3. COIL20数据库上的聚类实验结果

Table 4. Clustering experimental results on TDT2 database

表4. TDT2数据库上的聚类实验结果

4.3. 实验结果及实验结果分析

1) 表2~4分别为PIE、COIL20、TDT2三个数据集上的聚类实验。从表2中可以看出，DCCFS的平均AC和人平均NMI比基本的CF分别高6.63%和8.98%；比LCCF分别高出4.92%和7.8%；比GCF分别高2.46%和5.26%。从表3和表4中也能得到类似的数据，充分说明了DCCFS的优越性。

2) 从表2~4可以看出，LCCF的聚类性能比基本的CF算法优秀，这是由于LCCF采用了流形学习的思想，保证了数据内部的几何结构不变，因此实验所展现出的LCCF聚类性能较CF优越；GCF在LCCF的基础上，不仅考虑了单边流形，同时考虑了双边流形，这说明了不仅保持原有数据空间的几何结构信息不变可以提高算法的学习质量，保持特征空间的几何结构信息同样也能增强效果，使得算法具有了更加优秀的数据挖掘能力，因此性能比LCCF更好。

3) 本章提出的DCCFS比GCF的聚类性能更好，主要原因是DCCFS考虑到了数据的标签信息以及算法分解的稀疏性。前者通过构造受限矩阵对标签信息施加硬约束，使得高维空间中属于同一类的样本可以投影到低维空间中的同一点上，将原本无监督的算法改造成了半监督的算法，提高了算法的鉴别能力和学习能力，后者通过人为添加 $L_P$ 平滑约束， $L_P$ 利用 $L_1$ 范数可以有效增加稀疏， $L_2$ 范数可以有效增加平滑的特点提高了算法的稀疏性，使得算法分解平稳、平滑、精确。

4.4. 参数选择

本文提出的DCCFS模型包含了四个参数 $\alpha ,\lambda ,\mu ,P$ ，因此需要研究模型对四个参数的敏感性。在CDNMFS模型中 $\alpha ,\lambda$ 是对偶图参数，为方便起见，这里只需二者的值相等，即 $\alpha =\lambda$。设置P的取值为 $1<P<2$ ，设置 $\mu =\left(0,1,1,10,100,1000,2000\right)$。实验结果如图1~3所示，可以得到如下结论：

Figure 1. Evaluation experiment of regular term parameter $\alpha =\lambda$

图1. 正则项参数 $\alpha =\lambda$ 的评估实验

Figure 2. Evaluation experiment of regular term parameter P

图2. 正则项参数P的评估实验

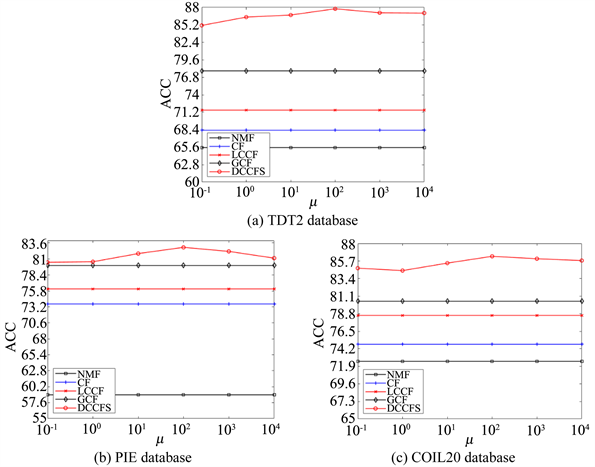
Figure 3. Evaluation experiment of regular term parameter $\mu$

图3. 正则项参数 $\mu$ 的评估实验

1) 本文提出的DCCFS对于正则项参数 $\alpha$ 和 $\lambda$ 具有较好的不敏感性。从图1中可以看出，当两正则项参数取1~1000时，DCCFS可以取到较好的聚类性能，当超过1000时算法性能开始下降，但比其他同类算法优秀。

2) NMF、CF、LCCF、GCF的算法不含平滑约束，因此模型中不含P参数，所以这四种算法的聚类性能不随P值的变化而变化。从图2中可以看出，DCCFS的性能在大部分情况都很稳定且具有很高的性能，说明了DCCFS在P取值为1至2之间时实验效果理想。

3) 同理，NMF、CF、LCCF、GCF算法性能也不随 $\mu$ 的变化而变化。从图3中可以看出，无论 $\mu$ 取何值，DCCFS的聚类性能均优于其他算法，充分证明了对算法施加稀疏约束的设想是合理的。

5. 结论

本文主要做了以下工作：针对传统的CF算法无法在低维空间中保持原始空间中的几何结构信息、无法有效利用样本中实际存在的类别信息以及没有足够的稀疏性，本文提出了一种基于稀疏约束和对偶图正则化的受限概念分解算法(DCCFS)。本方法结合流形学习的思想在算法进行图像表达时添加对偶图正则项，进一步利用样本中的先验知识，考虑数据空间与特征空间的几何结构信息，通过构造了对偶图，使得算法的数据表示能力进一步得到了提升，可以挖掘出数据中蕴含的本质特征，提高了算法的聚类性能；为了利用数据中存在的标签性息，通过构造受限矩阵对标签信息施加硬约束，使得高维空间中属于同一类的样本可以投影到低维空间中的同一点上，将原本无监督的算法改造成半监督的算法。最后考虑到CF算法对稀疏性考虑的不够，DCCFS通过添加 $L_P$ 平滑约束，有效增加稀疏、有效增加平滑的特点使得算法可以学习数据的稀疏表示，使分解后的样本具有较高的稀疏性，算法分解平稳，分解结果平滑、精确。在三个公共数据集上的实验证明了本文提出CDDFS的有效性。

基金项目

国家自然科学青年基金，项目批准号：61902160，项目名称：基于潜在表示的不完整多视图子空间学习方法研究。