容斥原理的两种证法及其应用

Two Proof Methods of the Principle of Inclusion-Exclusion and Their Applications

摘要: 这篇文章首先介绍容斥原理的内容，然后引入需要证明容斥原理的相关概念和定理。当前国内的文献对容斥原理的证明方法一般采取归纳法，本文采用了两种方法证明容斥原理，一种是从归纳法的角度证明。另外一种方法不同于当前大部分文献，从集合元素的角度入手分析证明容斥原理。在证明出容斥原理后，我们从相关文献中摘取两个与容斥原理的例子，来具体说明容斥原理的应用。

Abstract: This article first introduces the content of the inclusion-exclusion theorem, and then introduces the related concepts that need to be proved. In the current domestic literature, the proof method of the inclusion-exclusion theorem generally adopts the induction method. In this paper, two methods are used to prove the principle of inclusion and exclusion. One is to prove it by induction. The other method is different from most of the current literature, which analyzes and proves the principle of inclusion and exclusion from the perspective of set elements. After proving the inclusion-exclusion theorem, we extract two examples of the inclusion-exclusion theorem from the relevant literature to illustrate the application of the inclusion-exclusion theorem.

1. 引言

计数问题在组合数学中是热点探讨的问题。在计数的过程中，人们常常会把一些项目重复核算，使得被计算的数值出错。因此人们在实践的过程中逐渐摸索出一种新的核算数值项目的方法，这种方法称作容斥原理。容斥原理主要内容为在不考虑重复的条件下，把需要核算出符合某种条件的所有对象一一核算出来，然后再把核算过程中重复的部分排斥出去，这样能够使得核算的结果既没有少计也没有多计。

这篇文章在参考国内外文献的基础上，给出容斥定理的两种证明方法，其中一种方法不同于当前大 部分文献，从集合元素的角度来分析证明容斥原理。其过程虽然比较复杂，但是能给读者提供一种新的视角理解容斥原理，让读者在数学证明上从数学概念的定义上去证明数学原理本身。其次，容斥原理在生活中的应用范围很广，利用此方法能有效解决复杂的计数问题，让人们能够高效无误地核算数值。另外数学竞赛也多次从容斥原理的角度出题，具体可参考文献 [1] [2] [3] [4]。

这篇文章全篇的安排结构如下：本文第二部分介绍容斥原理的内容，并且介绍需要证明容斥原理的预备知识及相关定理；第三部分是本文的重点部分，即采取归纳法和元素分析法两种不同的方法来分别证明容斥原理，第四部分主要讲容斥原理具体的应用，第五部分归纳总结容斥原理以及未来展望。

2. 容斥原理的定理内容及证明预备知识

2.1. 容斥原理的内容

定理1用 $\left|B\right|$ 来表示集合B的元素个数，假设 $B_1,B_2,\cdots ,B_n$ 是有限集合 $T_n=B_1\cup B_2\cup \cdots \cup B_n$ 的子集，记集合 $\bar{B}$ 是集合B的补集，全集 $Q=B\cup \bar{B}$ ，容斥原理可用如下式子来表述：

$\left|{\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}\right|={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|B_i\right|}-{\displaystyle \underset{1\le i<j\le n}{\overset{n}{\sum }}\left|B_i\cap B_j\right|}+{\displaystyle \underset{1\le i<j<t\le k}{\overset{n}{\sum }}\left|B_i\cap B_j\cap B_t\right|}-\cdots +{\left(-1\right)}^{n-1}\left|B_{l_1}\cap B_{l_2}\cap \cdots \cap B_{l_n}\right|$ (1)

其中 ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}=B_1\cup B_2\cup \cdots \cup B_n$。

2.2. 证明容斥原理的预备知识

二项式定理对于任意的数值p、q， $p+q$ 的k次幂为：

${\left(p+q\right)}^k=\left(\begin{array}{c}k\\ 0\end{array}\right)p^k+\left(\begin{array}{c}k\\ 1\end{array}\right)p^{k-1}q+\left(\begin{array}{c}k\\ 2\end{array}\right)p^{k-2}{q}^2+\cdots +\left(\begin{array}{c}k\\ k\end{array}\right)p^k$ (2)

$\left(\begin{array}{c}k\\ m\end{array}\right)=\frac{k!}{m!\left(k-m\right)!}$ 被称作为二项式系数的正整数，其中阶乘 $n!=n\ast \left(n-1\right)\cdots 1$ ，且规定 $0!=1$。

集合运算基本性质

对于任意集合 $B_1,B_2,\cdots ,B_n$ ，集合 $S=B_1\cup B_2\cup \cdots \cup B_n$ ，定义差集为 $B_1-B_2:=\left\{y\in B_1:y\notin B_2\right\}$ ，集合运算具有如下性质：

分配律： $B_1\cup \left(B_2\cap B_3\right)=\left(B_1\cap B_2\right)\cup \left(B_1\cap B_3\right)$ ， $B_1\cap \left(B_2\cup B_3\right)=\left(B_1\cap B_2\right)\cup \left(B_1\cap B_3\right)$

得·摩根定律： $S-\left(B_1\cup B_2\right)=\left(S-B_1\right)\cap \left(S-B_2\right)$ ， $S-\left(B_1\cap B_2\right)=\left(S-B_1\right)\cup \left(S-B_2\right)$

3. 容斥原理的证明方法

3.1. 数学归纳法

常见容斥定理的证明方法是采取归纳法进行相关的证明，以下利用数学归纳法对定理1的证明。证明的过程如下：

1) 当 $n=1$ 时， $\left|B_1\right|=\left|B_1\right|$ ，显然成立；当 $n=\text{2}$ 时， $\left|B_1\cup B_{\text{2}}\right|=\left|B_1\right|\text{+}\left|B_2\right|-\left|B_1\cap B_{\text{2}}\right|$ 可证明成立。

2) 假设当 $n\le k\left(k\ge 2\right)$ 时，等式两边成立，即

$\left|{\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}\right|={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|B_i\right|}-{\displaystyle \underset{1\le i<j\le n}{\overset{n}{\sum }}\left|B_i\cap B_j\right|}+{\displaystyle \underset{1\le i<j<t\le k}{\overset{n}{\sum }}\left|B_i\cap B_j\cap B_t\right|}-\cdots +{\left(-1\right)}^{n-1}\left|B_{l_1}\cap B_{l_2}\cap \cdots \cap B_{l_n}\right|$ (3)

3) 现在要证明 $n=k+1$ ，等式两边也成立，令 $T_k=B_1\cup B_2\cup \cdots \cup B_k$。当 $n=k+1$ 时，容斥原理的式子左边 $\left|T_k\cup B_{k+1}\right|$ 根据证明过程中第一步 $\left|B_1\cup B_{\text{2}}\right|=\left|B_1\right|\text{+}\left|B_2\right|-\left|B_1\cap B_{\text{2}}\right|$ ，可以写成： $\left|T_k\cup B_{k+1}\right|=\left|T_k\right|\text{+}\left|B_{k+1}\right|-\left|T_k\cap B_{k+1}\right|$ ，根据集合运算的相关性质可以得到：

$T_k\cap B_{k+1}=\left(B_1\cup B_2\cup \cdots \cup B_n\right)\cap B_{k+1}=\left(B_1\cap B_{k+1}\right)\cup \left(B_2\cap B_{k+1}\right)\cup \cdots \cup \left(B_k\cap B_{k+1}\right)$ (4)

把 $B_1\cap B_{k+1}$ 当成一个集合整体，由假设 $n\le k$ 可知：

$\begin{array}{c}\left|T_k\cap B_{k+1}\right|=\left|{\displaystyle \underset{i=1}{\overset{k}{\cup }}\left(B_i\cap B_{k+1}\right)}\right|={\displaystyle \underset{i=1}{\overset{k}{\sum }}\left|B_i\cap B_{k+1}\right|}-{\displaystyle \underset{1\le i<j\le k}{\overset{k}{\sum }}\left|B_i\cap B_j\cap B_{k+1}\right|}\\ +{\displaystyle \underset{1\le i<j<t\le k}{\overset{k}{\sum }}\left|B_i\cap B_j\cap B_t\cap B_{k+1}\right|}-\cdots +{\left(-1\right)}^{n-1}\left|B_{l_1}\cap B_{l_2}\cap \cdots \cap B_{l_k}\cap B_{l_{k+1}}\right|\end{array}$ (5)

将式子(5)代入 $\left|T_k\cup B_{k+1}\right|=\left|T_k\right|\text{+}\left|B_{k+1}\right|-\left|T_k\cap B_{k+1}\right|$ 中可以得到

$\left|{\displaystyle \underset{i=1}{\overset{k\text{+1}}{\cup }}{B}_i}\right|={\displaystyle \underset{i=1}{\overset{k\text{+1}}{\sum }}\left|B_i\right|}-{\displaystyle \underset{1\le i<j\le k+1}{\overset{k\text{+1}}{\sum }}\left|B_i\cap B_j\right|}+{\displaystyle \underset{1\le i<j<t\le k+1}{\overset{k\text{+1}}{\sum }}\left|B_i\cap B_j\cap B_t\right|}-\cdots +{\left(-1\right)}^{n-1}\left|B_{l_1}\cap B_{l_2}\cap \cdots \cap B_{l_k}\cap B_{l_{k+1}}\right|$ (6)

即证明 $n=k+1$ 时容斥原理式子成立。

3.2. 枚举法(元素法)

根据 $\left|B_{k+1}\right|$ 的定义可以知道， $\left|B_{k+1}\right|$ 的数值等于有限集合 $B_{k+1}$ 中所有元素的个数，因此我们可以逐个分析容斥定理等式左边集合中所有元素个数与等式右边集合中所有元素个数的关系，在讨论出所有的情况后，再全部进行证明即可得到相应的证明，证明如下：

对于任意一个元素x，分别分析这个元素与等式左边和右边集合的关系。对于容斥原理式子左边有限

集 ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}$ ，元素x要么包含于 ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}$ 要么不包含 ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}$ ，显然当元素不包含于 ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}$ 时，显然这个元素x也不

包含于右边所有的集合，故可知当核算这个元素x的个数时，等式两边成立，都为零。

当这个元素 $x_0$ 包含于 ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}$ 时，可假设有限集合的等价集合 $C_n=\left\{y|y\in {\displaystyle \underset{i=1}{\overset{n}{\cup }}{B}_i}\right\}$。然后分析元素x与集

合 $B_i\left(n\ge i\ge 1\right)$ 之间的关系。可知集合中 $C_n$ 的所有元素可分类为成如下的各个部分，对于任意给定的一个元素 $x\in C_n$ ：元素x只包含于一个 $B_i\left(n\ge i\ge 1\right)$ 中，元素x只包含于两个 $B_i$ 中，元素x只包含于三个 $B_i$ 中，…，元素x只包含于n个 $B_i$ 中。下面进行逐个证明：

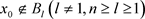1) 当元素x只包含于一个 $B_i$ 中，可假设元素 $x_0$ 只包含于 $B_1$ ，由于元素 $x_0$ 与集合 $B_1$ 的选取具有任意性，其他的证明方法可以类似。因为元素 $x_0$ 只包含于 $B_1$ 中，故 $x_0\in B_1$ ，。根据集合交集的定义，可知当核算这个元素 $x_0$ 的个数时，左边式子等于1，右边式子也等于1。

2) 当元素x只包含于两个 $B_i$ 中，可假设元素 $x_0$ 包含于集合 $B_1$ 、 $B_{\text{2}}$ ，由于元素 $x_0$ 与集合 $B_1$ 、 $B_{\text{2}}$ 的选取具有任意性，其他的证明方法可以类似。因为元素 $x_0$ 只包含于 $B_1$ 、 $B_{\text{2}}$ 中，故 $x_0\in B_1$ ， $x_0\in B_2$ ， $x_0\notin B_l\left(l\ne 1,l\ne 2,n\ge l\ge 1\right)$。根据集合交集的定义，可知当核算这个元素 $x_0$ 的个数时，左边式子等于1，

右边 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|B_i\right|}=2$ ， ${\displaystyle \underset{1\le i<j\le n}{\overset{n}{\sum }}\left|B_i\cap B_j\right|}=1$ ， ${\displaystyle \underset{1\le i<j<t\le k+1}{\overset{k\text{+1}}{\sum }}\left|B_i\cap B_j\cap B_t\right|}=0$ ， $\cdots$。即右边式子的数值等于2 − 1 = 1等于左边，即证。

3) 故证明可以推广，当元素x只包含于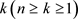个 $B_i$ 中，可假设元素 $x_0$ 只包含于 $B_1$ 、 $B_2$ 、 $\cdots$ 、 $B_k$ ，由于元素x与集合 $B_1$ 、 $B_2$ 、 $\cdots$ 、 $B_k$ 的选取具有任意性，其他的证明方法可以类似。因为元素 $x_0$ 只包含于 $B_1$ 、 $B_2$ 、 $\cdots$ 、 $B_k$ 中，故 $x_0\in B_1$ ， $x_0\in B_2$ ， $\cdots$ ， $x_0\in B_k$ ，。根

据集合交集的定义，可知当核算这个元素 $x_0$ 的个数时，左边式子等于1，右边 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|B_i\right|}=k$ ， ${\displaystyle \underset{1\le i<j\le n}{\overset{n}{\sum }}\left|B_i\cap B_j\right|}=\left(\begin{array}{c}k\\ 2\end{array}\right)$ ， ${\displaystyle \underset{1\le j_1<j_2<j_3\le n}{\overset{n}{\sum }}\left|B_{j_1}\cap B_{j_2}\cap B_{j_3}\right|}=\left(\begin{array}{c}k\\ 3\end{array}\right)$, $\cdots$, ${\displaystyle \underset{1\le j_1<j_2<j_3<\cdots <j_k\le n}{\overset{n}{\sum }}\left|B_{j_1}\cap B_{j_2}\cap B_{j_3}\cap \cdots \cap B_{j_k}\right|}=1$。

将右边式子重新整理一遍可以得到： $\left(\begin{array}{c}k\\ 1\end{array}\right)-\left(\begin{array}{c}k\\ 2\end{array}\right)+\left(\begin{array}{c}k\\ 3\end{array}\right)-\cdots +{\left(-1\right)}^{k-2}\left(\begin{array}{c}k\\ k-1\end{array}\right)+{\left(-1\right)}^{k-1}\left(\begin{array}{c}k\\ k\end{array}\right)$ ，根据二项式定理可以得到：

${\left(p+q\right)}^k=\left(\begin{array}{c}k\\ 0\end{array}\right)p^k+\left(\begin{array}{c}k\\ 1\end{array}\right)p^{k-1}q+\left(\begin{array}{c}k\\ 2\end{array}\right)p^{k-2}{q}^2+\cdots +\left(\begin{array}{c}k\\ k\end{array}\right)p^k$ (7)

令p = 1, q = −1时，可以得到：

${\left(1+\left(-1\right)\right)}^k=\left(\begin{array}{c}k\\ 0\end{array}\right)1^k+\left(\begin{array}{c}k\\ 1\end{array}\right)1^{k-1}\left(-1\right)+\left(\begin{array}{c}k\\ 2\end{array}\right)1^{k-2}{\left(-1\right)}^2+\cdots +\left(\begin{array}{c}k\\ k\end{array}\right)1^k$ (8)

故右边式子：

$\left(\begin{array}{c}1\\ k\end{array}\right)-\left(\begin{array}{c}2\\ k\end{array}\right)+\left(\begin{array}{c}3\\ k\end{array}\right)-\cdots +{\left(-1\right)}^{k-2}\left(\begin{array}{c}k-1\\ k\end{array}\right)+{\left(-1\right)}^{k-1}\left(\begin{array}{c}k\\ k\end{array}\right)+1-1=-{\left(1+\left(-1\right)\right)}^k+1$ (9)

即证定理1。

4. 容斥定理的应用

求相关数值的整除解的个数

例1求5000以下正整数中能被7整除或者被12整除的数值的个数。

解答：记事件A = {5000以下的正整数中能被8整除的数}，事件B = {5000以下的正整数中能被12整除的数}，可知 $\left|A\cup B\right|$ 即为我们这道题目所要求解的答案。

根据相关计算可以得到：

$\left|A\right|=\left[5000/8\right]=714$ ， $\left|B\right|=\left[5000/12\right]=416$ ， $\left|A\cap B\right|=\left[5000/84\right]=59$

(函数 $\left[p\right]$ 是取整函数，这个函数表示的意思是不超过任意给定的数值p的最大整数值，例如 $\left[1.23\right]=1$ ， $\left[2.23\right]=2$ )，所有5000以下正整数中能被7整除或者能被12整除的数值个数为：

$\left|A\cup B\right|=\left|A\right|+\left|B\right|-\left|A\cap B\right|=1071$

这是容斥定理的一个简单应用，此外容斥定理还广泛应用于日常生活当中。

根据参考文献 [5] 的一个例题：

例2在一所中学中有15名老师教授数理化，在这15名老师中，已知教授数学的老师有8名，教授物理学科的有7名，教授化学学科的有6名，且有4名老师教2门学科，试问：同时教授数学、物理和化学学科的老师有多少名？

证明：记事件A = {教授数学学科的老师}，事件B = {教授物理学科的老师}，事件C = {教授化学学科的老师的}。根据题意可以知道 $\left|A\right|=8$ ， $\left|B\right|=7$ ， $\left|C\right|=6$ ， $\left|A\cap B\right|+\left|A\cap C\right|+\left|C\cap B\right|=4$ ，根据容斥定理可以知道 $\left|A\cap B\cap C\right|=\left|A\right|+\left|B\right|+\left|C\right|-\left(\left|A\cap B\right|+\left|A\cap C\right|+\left|C\cap B\right|\right)-\left|A\cup B\cup C\right|=2$。故同时教授数学、物理和化学学科的老师有2名。

5. 总结

本文采取了两种证明方法来证明容斥原理，其中数学归纳法是当前大部分文献所采取的证明方法，另外一种方法不同于当前大部分文献，从集合元素的角度来分析容斥原理，虽然以集合元素的角度来分析证明的过程比较复杂，但是希望能够提供一种新的视角来理解容斥原理，让读者在数学证明上，能从数学概念的定义上去证明数学原理本身。此定理的第二种证明方法也能给读者另外一种角度，将容斥原理应用于生活中。类比本文元素分析法的过程，将生活中的计数问题逐一分类，再进行求解，从而高效无误的解决问题。