具有未知参数和时变拓扑的复杂网络同步研究

Synchronization of Complex Networks with Unknown Parameters and Time-Varying Topology

摘要: 本文利用Lyapunov稳定性理论以及自适应控制等方法，针对具有未知参数和时变拓扑的复杂网络同步控制问题进行研究。首先，提出的复杂网络模型是全新的，模型同时考虑了未知参数和时变拓扑的影响；其次，针对提出的复杂网络模型，通过设计合适的自适应控制器，基于Lyapunov稳定性理论，分别得到了复杂网络实现完全同步和反同步的充分条件；最后，针对复杂网络的自适应控制完全同步和反同步，给出了两个仿真例子验证了结论的正确性。

Abstract: In this paper, the Lyapunov stability theory and adaptive control method are used to study the synchronization control problem of complex networks with unknown parameters and time-varying topology. Firstly, the proposed complex network model is completely new, which considers the influence of unknown parameters and time-varying topology simultaneously. Secondly, based on Lyapunov stability theory, sufficient conditions for complete synchronization and anti-synchronization of complex network are obtained by designing appropriate adaptive controller. Finally, two simulation examples are given to verify the correctness of the conclusion for the complete synchronization and anti-synchronization of adaptive control in complex networks.

1. 引言

1.1. 复杂网络同步的介绍

同步是自然界中普遍存在且十分重要的一类非线性物理现象，按照所研究的网络系统数量，可以将网络同步分为两类，一类是研究一个网络系统的同步，即内部同步，另一类是研究两个网络系统间的同步，即外部同步。有关同步的研究成果有很多，学者们研究了外同步 [1] [2] [3]、指数同步 [4] [5] [6] [7] [8]、全局同步 [9] [10]、混合同步 [11] [12]、完全同步 [13]、反同步 [14] 等。其中，完全同步是生活中最普遍的一种同步。同步在激光系统、超导材料和通信系统等领域中起着重要作用。

1.2. 复杂网络同步的研究意义

随着计算机技术和网络理论研究的快速发展，复杂动态网络的同步研究受到了很多学者和科研人员的关注，是复杂动态网络研究中的一个重要课题，在工程界和科学界发挥着非常重要的作用。在实际生活中，绝大多数网络都不是静态的，如互联网、DNA等，这些都是时变的。而且网络不确定性有很多，如参数的不确定性、动态不确定性 [15]、网络节点的不确定性、边的连接具有不可分辨性 [16] 等。同步在核磁共振仪、激光系统、超导材料和通信系统等领域起着非常重要的作用。本文主要的研究内容为时变的复杂动态网络同步问题，研究目的是为解决物理问题或生物工程等提供理论基础。

1.3. 本文的主要工作和结构

两个耦合的非线性时变复杂动态网络达到完全同步以及反同步是本章的主要研究内容，在自适应控制器的应用下，基于Lyapunov稳定性理论，达到网络的同步。

第一章主要介绍了复杂网络的同步现象、复杂网络同步的研究意义，并简单的介绍了本文的主要工作和结构。

第二章研究了复杂动态的网络同步现象，同时考虑未知参数和时变拓扑的影响，提出了全新的具有时变内耦合和非线性外耦合的复杂网络模型，并给读者定义同步与反同步及相关假设。

第三章通过构造自适应控制器，并基于Lyapunov稳定性理论，建立Lyapunov函数，证明了该复杂网络模型可达到同步与反同步，满足同步解是渐进稳定的。

第四章利用MATLAB进行数值仿真实验，选择了Chua系统进行数值模拟，进一步证明了理论分析的正确性。

2. 网络模型的建立与假设

2.1. 网络模型的建立

考虑一个具有时变内耦合和非线性外耦合的复杂动态网络，考虑以下动力学方程：

${\stackrel{\dot{}}{x}}_i\left(t\right)=f_1\left(x_i\left(t\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1+c{\displaystyle \underset{j=1;j\ne i}{\overset{N}{\sum }}{a}_{ij}\left(t\right)\left(g\left(x_j\left(t\right)\right)-g\left(x_i\left(t\right)\right)\right)}$ (1)

其中 $x_i={\left(x_{i1},x_{i2},\cdots ,x_{in}\right)}^{\text{T}}\in R^n$ 是节点i的状态变量向量； $f_1(\cdot )$， $F(\cdot )\in R^n$ 是描述节点动力学的光滑非线性函数；c是耦合强度； $A\left(t\right)\in R^{n\times n}$ 是网络的时变耗散耦合矩阵，表示网络的拓扑结构，即若节点 $i,j\left(i\ne j\right)$ 有连接，则 $a_{ij}\left(t\right)>0$ 若无连接，则 $a_{ij}\left(t\right)=0$，用来描述网络的拓扑结构 [5]，且规定是耗散的，即

$\{\begin{array}{l}{a}_{ii}\left(t\right)=-{\displaystyle {\sum }_{i=1;j\ne i}^N{a}_{ij}\left(t\right)}\\ {\displaystyle {\sum }_{j=1}^N{a}_{ij}\left(t\right)}=0\end{array}$

则模型变为

${\stackrel{\dot{}}{x}}_i\left(t\right)=f_1\left(x_i\left(t\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1+c{\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_{ij}\left(t\right)g\left(x_j\left(t\right)\right)}+u_i\left(t\right)\left(i=1,2,\cdots ,N\right)$ (2)

其中 ${\theta }_1\in R^q$ 是未知参数可微函数向量，向量 $u_i\left(t\right)$ 是控制器。

设 $s\left(t\right)$ 是同步状态，可以是一个稳定点或者混沌吸引子的周期轨道，且方程满足：

$\stackrel{\dot{}}{s}\left(t\right)=f_1\left(s\left(t\right)\right)+F\left(s\left(t\right)\right){\theta }_2\left(i=1,2,\cdots ,n\right)$ (3)

其中 ${\theta }_2\in R^q$ 是未知参数可微函数向量。

由(2)和(3)得到时变的非线性耦合网络模型为：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_i\left(t\right)=f_1\left(x_i\left(t\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1+c{\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_{ij}\left(t\right)g\left(x_j\left(t\right)\right)}+u_i\left(t\right)\\ \stackrel{\dot{}}{s}\left(t\right)=f_1\left(s\left(t\right)\right)+F\left(s\left(t\right)\right){\theta }_2\left(i=1,2,\cdots ,N\right)\end{array}$ (4)

其中， ${\theta }_i\in R^q\left(i=1,2\right)$ 是未知参数可微函数向量。

下面给出完全同步定义如下：

定义1：设 $\{\begin{array}{l}{x}_i={\left(x_{i1},x_{i2},\cdots ,x_{in}\right)}^{\text{T}}\in R^n\\ y_i={\left(y_{i1},y_{i2},\cdots ,y_{in}\right)}^{\text{T}}\in R^n\end{array}$ 是节点i的状态变量向量，如果网络中的所有节点随时间的变化趋于一致，即

$\underset{t\to \infty }{\lim }\Vert y_i\left(t\right)-x_i\left(t\right)\Vert =0\left(i=1,2,\cdots ,N\right)$

则称复杂网络实现了完全同步。

下面给出反同步定义如下：

定义2：设 $\{\begin{array}{l}{x}_i={\left(x_{i1},x_{i2},\cdots ,x_{in}\right)}^{\text{T}}\in R^n\\ y_i={\left(y_{i1},y_{i2},\cdots ,y_{in}\right)}^{\text{T}}\in R^n\end{array}$ 是节点i的状态变量向量，如果网络中的所有节点随时间的演进完全相反，即：

$\underset{t\to \infty }{\lim }\Vert y_i\left(t\right)+x_i\left(t\right)\Vert =0\left(i=1,2,\cdots ,N\right)$

则称复杂网络实现了反同步。

2.2. 相关假设与引理

为了得到主要结果，我们给出了以下必要的假设和引理。

假设1 [14]：假设存在正数L，M，使非线性函数 $f(\cdot )$， $g(\cdot )$，满足：

$\begin{array}{l}\Vert f\left(y_i\left(t\right)\right)-f\left(x_i\left(t\right)\right)\Vert \le L\Vert y_i\left(t\right)-x_i\left(t\right)\Vert \\ \Vert g\left(y_j\left(t\right)\right)-g\left(x_i\left(t\right)\right)\Vert \le M\Vert y_i\left(t\right)-x_i\left(t\right)\Vert ,\end{array}$

其中 $x_i\left(t\right),y_i\left(t\right)\in R^n$ 是时变向量，其中 $\Vert ·\Vert$ 为欧几里德范数。

假设2：对于非线性函数 $f\left(x\right)$ 关于x是奇函数，既满足： $f\left(x\right)=-f\left(-x\right)$，其中 $x\in R^n$ 是时变向量。

引理1 [17]：(Schur complement)线性矩阵不等式

$\left(\begin{array}{ll}A\left(x\right)\hfill & B\left(x\right)\hfill \\ B^{\text{T}}\left(x\right)\hfill & C\left(x\right)\hfill \end{array}\right)<0$

其中 $A\left(x\right)={\left(A\left(x\right)\right)}^{\text{T}}$， $C\left(x\right)={\left(C\left(x\right)\right)}^{\text{T}}$ 等价于以下不等式：

$\begin{array}{l}(1):A\left(x\right)<0,C\left(x\right)-B{\left(x\right)}^{\text{T}}A{\left(x\right)}^{-1}B\left(x\right)<0\\ (2):C\left(x\right)<0,A\left(x\right)-B\left(x\right)C{\left(x\right)}^{-1}B{\left(x\right)}^{\text{T}}<0\end{array}$

引理2 [18]：对于任意的对阵正定矩阵 $Q\in R^{N\times N}$ 和 $x,y\in R^n$，有

$\pm 2x^{\text{T}}y\le x^{\text{T}}Qx+y^{\text{T}}{Q}^{-1}y$.

引理3 [19]：若耗散耦合矩阵A满足 $a_{ij}\left(t\right)\ge 0,i,j\left(i\ne j\right),i=1,2,\cdots ,N$，则有：

1) 矩阵A的特征值为0，特征向量为 ${\left(1,1,\cdots ,1\right)}^{\text{T}}$；

2) 矩阵A的特征值实部小于等于零，且所有特征值实部为零的那些特征值是实特征值0；

3) 矩阵A是不可约矩阵，则A特征值的重数为1。

说明1：根据引理1.1，A的特征值满足 ${\lambda }_1\left(t\right)=0$ 和 $\mathrm{Re}\left({\lambda }_k\left(t\right)\right)>0\left(k=2,3,\cdots ,N\right)$。

引理4：设 $\left\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\right\}$ 和 $\left\{{\mu }_1,{\mu }_2,\cdots ,{\mu }_n\right\}$ 分别为耦合矩阵A、B的特征值，则 $A\otimes B$ 的特征值为 ${\lambda }_i{u}_j$ 且满足： $\left|{\lambda }_{\min }\right|\left|{\mu }_{\min }\right|\le A\otimes B\le \left|{\lambda }_{\max }\right|\left|{\mu }_{\max }\right|$。其中 $\otimes$ 是Kroneker积运算；max和min分别表示最大和最小特征值范数。

假设3：假设扩散耦合矩阵 $A\left(t\right)$ 的特征值关于时间参数t一致有界。即存在 $M>0$，对任意的 $t>0$，有 $\left|\lambda \left(A\left(t\right)\right)\right|\le M$。

3. 主要结果

我们利用自适应控制器并基于Lyapunov理论，构造Lyapunov函数 $V\left(t\right)$，若 $\stackrel{\dot{}}{V}\left(t\right)<0$ 则表示系统是渐进稳定的。由于构造Lyapunov函数并没有具体的规律和公式，因此需要借助前人对复杂网络同步的稳定性研究 [20]，根据已掌握的技巧构造出Lyapunov函数，证明系统是渐近稳定的。

3.1. 自适应控制下网络的完全同步

定义系统误差变量为：

$e_i\left(t\right)=x_i\left(t\right)-s\left(t\right),i=1,2,\cdots ,N$ (5)

构造自适应控制器：

$\{\begin{array}{l}{u}_i\left(t\right)=-k_i\left(t\right)e_i\left(t\right)\\ {\stackrel{\dot{}}{k}}_i\left(t\right)=h_i{e}_i^{\text{T}}\left(t\right)e_i\left(t\right)\\ {\stackrel{\dot{}}{\theta }}_1=-{\eta }_i{F}^{\text{T}}\left(x_i\right)e_i\left(t\right)\\ {\stackrel{\dot{}}{\theta }}_2={\gamma }_i{F}^{\text{T}}\left(s\right)e_i\left(t\right)\end{array}i=1,2,\cdots ,N$ (6)

其中 $k_i\left(t\right)$ 是自适应函数， $h_i,{\eta }_i,{\gamma }_i$ 是待定常数。

定理1：如果假设1和假设3均成立，基于引理1到引理4，利用自适应控制器(6)并基于Lyapunov理论，来实现时变复杂动态网络的完全同步且保证同步解是渐进稳定的。

证明：复杂网络的误差系统：

$\begin{array}{c}{\stackrel{\dot{}}{e}}_i=x_i\left(t\right)-s\left(t\right)\\ =f_1\left(x_i\left(t\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1+c{\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_{ij}\left(t\right)g\left(x_j\left(t\right)\right)}+u_i\left(t\right)-\left(f_1\left(s\left(t\right)\right)+F\left(s\left(t\right)\right){\theta }_2\right)\\ =\left(f_1\left(x_i\left(t\right)\right)-f_1\left(s\left(t\right)\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1-F\left(s\left(t\right)\right){\theta }_2\\ +c{\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_{ij}\left(t\right)\left(g\left(x_j\left(t\right)\right)-g\left(s\left(t\right)\right)\right)}-k_i{e}_i\left(i=1,2,\cdots ,N\right)\end{array}$ (7)

构建Lyapunov函数：

$V\left(t\right)=\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{h_i}}{\left(k_i-k_i^{*}\right)}^2+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\eta }_i}{\theta }_1^{\text{T}}{\theta }_1}+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\gamma }_i}{\theta }_2^{\text{T}}{\theta }_2}$

其中， $k_i^{*}>0$，且为常数。

将 $V\left(t\right)$ 沿着误差系统(7)关于时间t求导得：

$\begin{array}{l}\stackrel{\dot{}}{V}\left(t\right)={\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{\stackrel{\dot{}}{e}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{h_i}}\left(k_i-k_i^{*}\right){\stackrel{\dot{}}{k}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\eta }_i}{\theta }_1^{\text{T}}{\stackrel{\dot{}}{\theta }}_1}+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\gamma }_i}{\theta }_2^{\text{T}}{\stackrel{\dot{}}{\theta }}_2}\\ ={\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}\left[\left(f_1\left(x_i\left(t\right)\right)-f_1\left(s\left(t\right)\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1-F\left(s\left(t\right)\right){\theta }_2+c{\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_{ij}\left(t\right)\left(g\left(x_j\left(t\right)\right)-g\left(s\left(t\right)\right)\right)}-k_i{e}_i\right]\\ +{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(k_i-k_i^{*}\right)e_i^{\text{T}}{e}_i}-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\theta }_1^{\text{T}}}{F}^{\text{T}}\left(x_i\left(t\right)\right)e_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\theta }_2^{\text{T}}}{F}^{\text{T}}\left(s\left(t\right)\right)e_i\\ ={\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}\left(f_1\left(x_i\left(t\right)\right)-f_1\left(s\left(t\right)\right)\right)-k_i^{*}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i+c{e}^{\text{T}}\left(t\right)\left(A\left(t\right)\otimes I_N\right)\left(g\left(x\left(t\right)\right)-g\left(s\left(t\right)\right)\right)\end{array}$

$\begin{array}{l}\le L{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i-k_i^{*}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i+c\frac{\xi }{2}{e}^{\text{T}}\left(t\right)\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\otimes I_N\right)e\left(t\right)+\frac{c{M}^2}{2\xi }{e}^{\text{T}}\left(t\right)e\left(t\right)\\ \le L{e}^{\text{T}}\left(t\right)e\left(t\right)-k^{*}{e}^{\text{T}}\left(t\right)e\left(t\right)+c\frac{\xi }{2}{\lambda }_{\max }\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\right)e^{\text{T}}\left(t\right)e\left(t\right)+\frac{c{M}^2}{2\xi }{e}^{\text{T}}\left(t\right)e\left(t\right)\\ =\left(L-k^{*}+c\frac{\xi }{2}{\lambda }_{\max }\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\right)+\frac{c{M}^2}{2\xi }\right)e^{\text{T}}\left(t\right)e(\; t\; )\end{array}$

记 $e={\left(e_1^{\text{T}},e_2^{\text{T}},\cdots ,e_N^{\text{T}}\right)}^{\text{T}}$， $g\left(x\left(t\right)\right)=\left(g\left(x_1\left(t\right)\right),g\left(x_2\left(t\right)\right),\cdots ,g\left(x_N\left(t\right)\right)\right)$， $g\left(s\left(t\right)\right)=\left(g\left(s\left(t\right)\right),g\left(s\left(t\right)\right)\cdots ,g\left(s\left(t\right)\right)\right)$， $k=\min \left\{k_1,k_2,\cdots ,k_N\right\}$，

这里Q取正常数 $\zeta$， $I_N$ 为单位矩阵， ${\lambda }_{\max }$ 是矩阵的最大特征值。

令 $k^{*}>L+\frac{c\xi }{2}{\lambda }_{\max }\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\right)+\frac{c{M}^2}{2\xi }$，则 $\stackrel{\dot{}}{V}\left(t\right)<-e^{\text{T}}e<0$。根据Lyapunov稳定性理论可得到复杂网络模型(4)实现完全同步且满足同步解是渐进稳定的，定理得证。

3.2. 自适应控制下网络的反同步

定义系统误差变量为：

$e_i\left(t\right)=x_i\left(t\right)+s\left(t\right),i=1,2,\cdots ,N$ (8)

构造自适应控制器：

$\{\begin{array}{l}{u}_i\left(t\right)=-k_i\left(t\right)e_i\left(t\right)\\ {\stackrel{\dot{}}{k}}_i\left(t\right)=h_i{e}_i^{\text{T}}\left(t\right)e_i\left(t\right)\\ {\stackrel{\dot{}}{\theta }}_1=-{\eta }_i{F}^{\text{T}}\left(x_i\right)e_i\left(t\right)\\ {\stackrel{\dot{}}{\theta }}_2=-{\gamma }_i{F}^{\text{T}}\left(s\right)e_i\left(t\right)\end{array}i=1,2,\cdots ,N$ (9)

其中 $k_i\left(t\right)$ 是自适应函数， $h_i,{\eta }_i,{\gamma }_i$ 是待定常数。

定理2：设假设1和假设3均成立，基于引理1到引理4，利用自适应控制器(9)并基于Lyapunov理论，来实现时变复杂动态网络的反同步且保证其同步解是渐进稳定的。

证明：复杂网络的误差系统：

$\begin{array}{c}{\stackrel{\dot{}}{e}}_i=x_i\left(t\right)+s\left(t\right)\\ =f_1\left(x_i\left(t\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1+c{\displaystyle \underset{j=1;j\ne i}{\overset{N}{\sum }}{a}_{ij}\left(t\right)g\left(x_j\left(t\right)\right)}+u_i\left(t\right)+\left(f_1\left(s\left(t\right)\right)+F\left(s\left(t\right)\right){\theta }_2\right)\\ =\left(f_1\left(x_i\left(t\right)\right)+f_1\left(s\left(t\right)\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1+F\left(s\left(t\right)\right){\theta }_2\\ +c{\displaystyle \underset{j=1;j\ne i}{\overset{N}{\sum }}{a}_{ij}\left(t\right)\left(g\left(x_j\left(t\right)\right)-g\left(s\left(t\right)\right)\right)}-k_i{e}_i\left(i=1,2,\cdots ,N\right)\end{array}$ (10)

构建Lyapunov函数为：

$V\left(t\right)=\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{h_i}}{\left(k_i-k_i^{*}\right)}^2+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\eta }_i}{\theta }_1^{\text{T}}{\theta }_1}+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\gamma }_i}{\theta }_2^{\text{T}}{\theta }_2}$

其中， $k_i^{*}>0$，且为常数。

将 $V\left(t\right)$ 沿着误差系统(10)关于时间t求导得：

$\begin{array}{l}\stackrel{\dot{}}{V}\left(t\right)={\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{\stackrel{\dot{}}{e}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{h_i}}\left(k_i-k_i^{*}\right){\stackrel{\dot{}}{k}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\eta }_i}{\theta }_1^{\text{T}}{\stackrel{\dot{}}{\theta }}_1}+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{1}{{\gamma }_i}{\theta }_2^{\text{T}}{\stackrel{\dot{}}{\theta }}_2}\\ ={\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}\left[\left(f_1\left(x_i\left(t\right)\right)+f_1\left(s\left(t\right)\right)\right)+F\left(x_i\left(t\right)\right){\theta }_1+F\left(s\left(t\right)\right){\theta }_2+c{\displaystyle \underset{j=1;j\ne i}{\overset{N}{\sum }}{a}_{ij}\left(t\right)\left(g\left(x_j\left(t\right)\right)-g\left(s\left(t\right)\right)\right)}-k_i{e}_i\right]\\ +{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(k_i-k_i^{*}\right)e_i^{\text{T}}{e}_i}-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\theta }_1^{\text{T}}}{F}^{\text{T}}\left(x_i\left(t\right)\right)e_i-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\theta }_2^{\text{T}}}{F}^{\text{T}}\left(s\left(t\right)\right)e_i\\ ={\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}\left(f_1\left(x_i\left(t\right)\right)-f_1\left(-s\left(t\right)\right)\right)-k_i^{*}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i+c{e}^{\text{T}}\left(t\right)\left(A\left(t\right)\otimes I_N\right)\left(g\left(x\left(t\right)\right)-g\left(s\left(t\right)\right)\right)\end{array}$

$\begin{array}{l}\le L{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i-k_i^{*}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}{e}_i+c\frac{\xi }{2}{e}^{\text{T}}\left(t\right)\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\otimes I_N\right)e\left(t\right)+\frac{c{M}^2}{2\xi }{e}^{\text{T}}\left(t\right)e\left(t\right)\\ \le L{e}^{\text{T}}\left(t\right)e\left(t\right)-k^{*}{e}^{\text{T}}\left(t\right)e\left(t\right)+c\frac{\xi }{2}{\lambda }_{\max }\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\right)e^{\text{T}}\left(t\right)e\left(t\right)+\frac{c{M}^2}{2\xi }{e}^{\text{T}}\left(t\right)e\left(t\right)\\ =\left(L-k^{*}+c\frac{\xi }{2}{\lambda }_{\max }\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\right)+\frac{c{M}^2}{2\xi }\right)e^{\text{T}}\left(t\right)e(\; t\; )\end{array}$

记 $e={\left(e_1^{\text{T}},e_2^{\text{T}},\cdots ,e_N^{\text{T}}\right)}^{\text{T}}$， $g\left(x\left(t\right)\right)=\left(g\left(x_1\left(t\right)\right),g\left(x_2\left(t\right)\right),\cdots ,g\left(x_N\left(t\right)\right)\right)$， $g\left(s\left(t\right)\right)=\left(g\left(s\left(t\right)\right),g\left(s\left(t\right)\right)\cdots ,g\left(s\left(t\right)\right)\right)$， $k=\min \left\{k_1,k_2,\cdots ,k_N\right\}$，

这里Q取正常数 $\zeta$， $I_N$ 为单位矩阵， ${\lambda }_{\max }$ 是矩阵的最大特征值。

令 $k^{*}>L+\frac{c\xi }{\text{2}}{\lambda }_{\max }\left(A\left(t\right)A{\left(t\right)}^{\text{T}}\right)+\frac{c{M}^2}{\text{2}\xi }$，则 $\stackrel{\dot{}}{V}\left(t\right)<-e^{\text{T}}e<0$。根据Lyapunov稳定性理论得到复杂网络模型(4)可以实现反同步且满足同步解是渐进稳定的，定理得证。

4. 数值仿真

4.1. 完全同步的数值仿真

为验证上述系统完全同步理论的正确性，选择Chua系统作为节点的动力学系统，数值模拟过程如下：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1\left(t\right)=\alpha \left(-x_1\left(t\right)+x_2\left(t\right)-\Phi \left(x_1\left(t\right)\right)\right)\hfill \\ {\stackrel{\dot{}}{x}}_2\left(t\right)=\theta x_1\left(t\right)-x_2\left(t\right)+x_3\left(t\right)\hfill \\ {\stackrel{\dot{}}{x}}_3\left(t\right)=-\beta x_2(\; t\; )\hfill \end{array}$

其中 $\Phi \left(x_1\left(t\right)\right)=a{x}_1\left(t\right)+\frac{1}{2}\left(a-b\right)\left[\left|x_1\left(t\right)+1\right|-\left|x_1\left(t\right)-1\right|\right]$， $\alpha =10$， $\beta =18$， $a=-3/4$， $b=-4/3$， $\theta =1$。

基于四阶Runge-kutta方法具有高精度特点，我们用其求解该微分方程组。其中，自适应控制器的自适应控制率 ${\stackrel{\dot{}}{k}}_i\left(t\right)=h_i{e}_i^{\text{T}}\left(t\right)e_i\left(t\right)$， $k_i\left(0\right)=5$。分别选择自适应控制因子 $h_i=4$ 和 $h_i=12$，其复杂网络模型的完全同步误差 $e_i$ 随时间变化如下图所示。

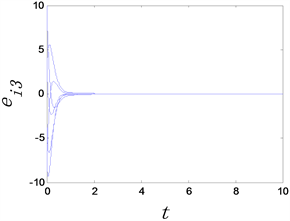
(a) 完全同步误差 $e_{i1}\left(t\right)$ (b) 完全同步误差 $e_{i2}(\; t\; )$ (c) 完全同步误差 $e_{i3}(\; t\; )$

Figure 1. The time evolution of complete synchronization errors of complex networks with adaptive controllers, where the adaptive controller factor $h_i=4$

图1. $h_i=4$ 时复杂网络的完全同步误差随时间变化图

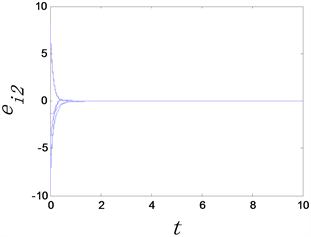
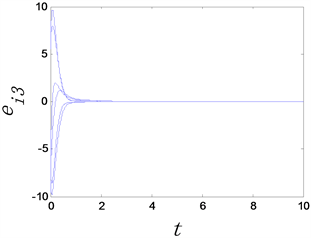
(a) 完全同步误差 $e_{i1}\left(t\right)$ (b) 完全同步误差 $e_{i2}(\; t\; )$ (c) 完全同步误差 $e_{i3}(\; t\; )$

Figure 2. The time evolution of complete synchronization errors of complex networks with adaptive controllers, where the adaptive controller factor $h_i=12$

图2. $h_i=12$ 时复杂网络的完全同步误差随时间变化图

从图1和图2中可以看出，无论选取 $h_i=4$ 还是 $h_i=12$ 复杂网络模型均可以达完全同步。这说明自适应控制器具有自动更新 $h_i$ 的作用。

4.2. 反同步的数值仿真

同样分别选择 $h_i=4$ 和 $h_i=12$ 的自适应控制因子，其复杂网络反同步误差 $e_i$ 随时间演化如下图所示。

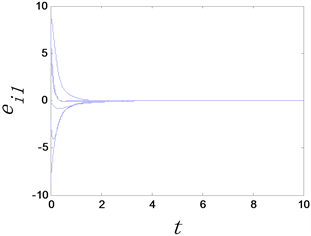
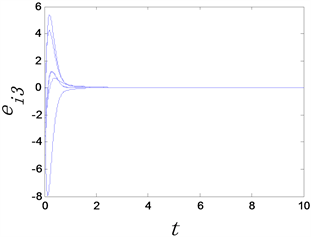
(a) 反同步误差 $e_{i1}\left(t\right)$ (b) 反同步误差 $e_{i2}(\; t\; )$(c) 反同步误差 $e_{i3}(\; t\; )$

Figure 3. The time evolution of anti-synchronization errors of complex networks with adaptive controllers, where the adaptive controller factor $h_i=4$

图3. $h_i=4$ 时复杂网络的反同步误差随时间变化图

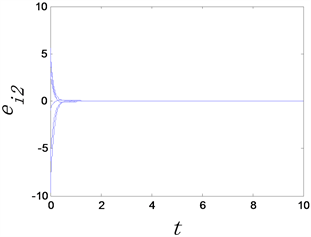
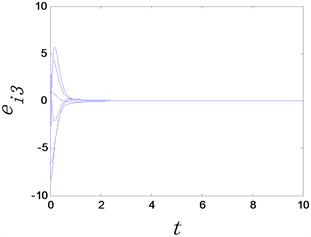
(a) 反同步误差 $e_{i1}\left(t\right)$ (b) 反同步误差 $e_{i2}(\; t\; )$ (c) 反同步误差 $e_{i3}(\; t\; )$

Figure 4. The time evolution of anti-synchronization errors of complex networks with adaptive controllers, where the adaptive controller factor $h_i=12$

图4. $h_i=12$ 时复杂网络的反同步误差随时间变化图

从图3和图4中可以看出，无论选取 $h_i=4$ 还是 $h_i=12$ 复杂网络模型均可以达到反同步。这说明自适应控制器具有自动更新 $h_i$ 的作用。

在仿真实验中，我们通过选择Chua系统进行数值模拟证明了理论分析的正确性，选择不同自适应因子进行模拟证明了自适应控制器自动更新控制因子的功能，说明了该自适应控制器相较于传统的控制方法如线性反馈控制、脉冲控制方法更具有自身的优势性。

5. 结论

本章主要研究复杂网络的完全同步和反同步问题，其中节点参数未知且拓扑结构是时变的。这一部分我们在选择模型时，由于在人们的生产生活中，时变的复杂网络最为常见，应用广泛，所以我们考虑了时变的复杂动态网络作为研究对象。创新点在于，我们采用了全新的时变复杂网络模型，从与其他学者研究 [17] [18] [19] [20] 的内容上比较，绝大多数的网络动态系统的模型假设网络具有规则和固定拓扑结构或者是含已知参数的时变拓扑结构，而本模型是在时变的复杂网络模型的基础上考虑了不确定参数的条件，使模型更贴近实际。

为得到网络完全同步以及反同步的充分条件，考虑构造误差系统，基于自适应控制器列出Lyapunov函数，借助于Lyapunov稳定性理论得到时变复杂动态网络同步且同步解是渐进稳定的。其中此处用的李雅普诺夫第二方法，相对于第一种更加直接简单。最后数值仿真实验验证结果的准确性。

基金项目

国家自然科学基金(批准号：62003189)、中国博士后科学基金(批准号：2020M672024)资助的课题。

NOTES

^*通讯作者。