Barzilai-Borwein型算法的探讨

Discussion on Barzilai-Borwein Algorithm

摘要: 本文介绍了八种负梯度算法，根据特点对其进行了比较，并对不同维数的严格凸二次函数进行了计算，绘制图表观察数据，发现BB型算法更具优势，维数越大优势越大。选取不同的初始步长可以改变算法的效果，特别是当矩阵条件数越大时，初始步长的选取越关键，本文考虑了四种选择初始步长的方法，分别将其放入算法中进行数值实验，结果表明，选取Hessian矩阵最小特征值的倒数效果最好。最后，介绍了负梯度算法在深度学习中的应用。

Abstract: This paper introduces eight kinds of negative gradient algorithms, compares them according to their characteristics, calculates strictly convex quadratic functions of different dimensions, draws graphs and observes data, and finds that BB algorithm is more advantageous, the larger the dimension is, the greater the advantage is. Selecting different initial step size can change the effect of the algorithm, especially when the number of matrix conditions is larger, the selection of the initial step size is more critical. This paper considers four methods of selecting the initial step size, and puts them into the algorithm for numerical experiments. The results show that the reciprocal of the minimum eigenvalue of the Hessian matrix is the best. Finally, the application of negative gradient algorithm in deep learning is introduced.

1. 引言

Barzilai-Borwein (BB)算法 [1] 是1988年提出的一种负梯度算法，它可以追溯到1847年Cauchy提出的最速下降法(SD) [2]，在当时产生了很大的影响。由于收敛速度慢，迭代次数过多，SD算法并没有引起人们的重视，为了提高负梯度算法的收敛速度，减少了迭代次数，Barzilai和Borwein提出了BB算法，并与SD进行了比较，给出了二次收敛和渐近收敛的证明，实验结果表明，BB算法在严格凸二次函数的极小化方面具有更强的竞争力。

BB算法提出后，负梯度算法越来越受到人们的关注。Raydan [3] 等人利用位移幂法(计算矩阵特征值和特征向量)，得到了BB算法对n维严格凸二次函数具有全局收敛性。Dai [4] 在Raydan等人的基础上进一步证明BB算法对n维严格凸二次函数收敛速度是R-线性收敛的，虽然这一结果没有SD算法的Q-线性速度，但BB算法的实际计算效果要远好于SD算法。在此基础上Fletcher [5] 等人通过忽略递归关系中的某些项，定义了该方法的简化版本，给出了n维BB算法的渐近收敛。

2003年Dai [6] 等人在BB算法的基础上，提出了交替使用BB步长的交替步梯度法(AS)，并分析在2维的情况下AS算法是两步Q-超线性收敛的，在n维情情况下AS算法是R-线性的收敛性，对比BB算法发现当矩阵A维数越大，AS算法的迭代次数比BB算法的迭代次数就越少，说明AS算法是一种很有潜力的BB型算法，为解决大规模问题提供了很好的选择。不仅如此在2006年预处理BB算法(ABB) [7] 提出，实验结果表明ABB算法明显优于已有BB型算法。本文在此基础上分析了多种负梯度算法，并应用到了不同维数的严格凸二次函数中，分析比较了数值结果，发现初始步长选择合适可以减少迭代次数和时间，数值结果表明不同的初始步长产生的迭代次数不同，为求解大规模问题提供了新的选择，例如信号处理 [8]、机器学习 [9] 和零售问题 [10] [11] [12]。

2. Barzilai-Borwein步长的选取

考虑严格凸二次函数的极小化问题：

$\underset{x\in {ℝ}^n}{\min }f\left(x\right)=\frac{1}{2}{x}^{\text{T}}Ax-b^{\text{T}}x$ (2.1)

中BB步长 ${\alpha }_k$ 是如何选取的，其中矩阵 $A\in {ℝ}^{n\times n}$ 是对称正定的，向量 $b\in {ℝ}^n$。利用SD算法和BB算法进行求解时，发现SD算法求解效果不好，尤其当A的条件数( $cond\left(A\right)=\Vert A\Vert \Vert A^{-1}\Vert$)很大时，效率很低，而BB算法表现良好。

负梯度算法的迭代格式均为 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$，其中 $a_k$ 表示步长， $\nabla f\left(x_k\right)$ 表示梯度，经过计算梯度可以写成 $\nabla f\left(x_k\right)=A{x}_k-b$。BB型算法的基本思想源于拟牛顿算法，它希望步长 $a_k$ 使矩阵 $D_k={\alpha }_{k}I$ 满足拟牛顿方程：

$D_k{s}_{k-1}=y_{k-1}$ (2.2)

记： $s_{k-1}=x_k-x_{k-1}$， $y_{k-1}=\nabla f\left(x_{k-1}\right)-\nabla f\left(x_{k-1}\right)$ (2.3)

设 $D_k$ 为函数 $f\left(x\right)$ 在 $x_k$ 点处的Hessian矩阵 $A_k$ 的逼近，利用上一步的迭代信息，使得矩阵 $D_k$ 具有一定的拟牛顿性质，在二范数的意义下取极小：

${\alpha }_k=\arg \underset{{\alpha }_k>0}{\min }{\Vert D_k^{-1}{s}_{k-1}-y_{k-1}\Vert }_2^2$ (2.4)

对这个极小化问题求解，并把解记为 ${\alpha }_k^{BB1}$ 得到：

${\alpha }_k^{BB1}=\frac{s_{k-1}^{\text{T}}{s}_{k-1}}{s_{k-1}{y}_{k-1}}$ (2.5)

根据对称性使得矩阵 $D_k$ 的逆 $D_k^{-1}$ 也有一定的拟牛顿性质，同样的在二范数的意义下取极小：

${\alpha }_k=\arg \underset{{\alpha }_k>0}{\min }{\Vert s_{k-1}-D_k{y}_{k-1}\Vert }_2^2$ (2.6)

对这个极小化问题求解，并把解记为 ${\alpha }_k^{BB2}$ 得到：

${\alpha }_k^{BB2}=\frac{s_{k-1}^{\text{T}}{y}_{k-1}}{y_{k-1}^T{y}_{k-1}}$ (2.7)

通常把 ${\alpha }_k^{BB1}$ 称为长BB步长，把 ${\alpha }_k^{BB2}$ 称为短的BB步长利用SD算法中：

$x_k-x_{k-1}=-{\alpha }_k\nabla f\left(x_k\right)$ (2.8)

$\nabla f\left(x_k\right)-\nabla f\left(x_{k-1}\right)=A\left(x_k-x_{k-1}\right)=A\left(-{\alpha }_k\nabla f\left(x_k\right)\right)$ (2.9)

带入到BB算法得到：

$s_{k-1}=x_k-x_{k-1}=-{\alpha }_k\nabla f\left(x_k\right)$ (2.10)

$y_{k-1}=\nabla f\left(x_k\right)-\nabla f\left(x_{k-1}\right)=A\left(x_k-x_{k-1}\right)=A\left(-{\alpha }_k\nabla f\left(x_k\right)\right)$ (2.11)

那么 ${\alpha }_k^{BB1}$ 可以写成：

${\alpha }_k^{BB1}=\frac{{\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}^{\text{T}}\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}{{\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}^{\text{T}}A\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}=\frac{\nabla f{\left(x_{k-1}\right)}^{\text{T}}\nabla f\left(x_{k-1}\right)}{\nabla f{\left(x_{k-1}\right)}^{\text{T}}A\nabla f\left(x_{k-1}\right)}$ (2.12)

同样的 ${\alpha }_k^{BB2}$ 可以写成：

${\alpha }_k^{BB2}=\frac{{\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}^{\text{T}}A\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}{{\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}^{\text{T}}{A}^{\text{T}}A\left(-{\alpha }_{k-1}\nabla f\left(x_{k-1}\right)\right)}=\frac{\nabla f{\left(x_{k-1}\right)}^{\text{T}}A\nabla f\left(x_{k-1}\right)}{\nabla f{\left(x_{k-1}\right)}^{\text{T}}{A}^2\nabla f\left(x_{k-1}\right)}$ (2.13)

与SD算法和MG (Minimum Gradient) [4] 算法的步长相比：

${\alpha }_k^{SD}=\arg \underset{{\alpha }_k>0}{\min }f\left(x_k-\alpha \nabla f\left(x_k\right)\right)=\frac{\nabla f{\left(x_k\right)}^{\text{T}}\nabla f\left(x_k\right)}{\nabla f{\left(x_k\right)}^{\text{T}}A\nabla f\left(x_k\right)}$ (2.14)

和

${\alpha }_k^{MG}=\arg \underset{{\alpha }_k>0}{\min }f\left(x_k-\alpha \nabla f\left(x_k\right)\right)=\frac{\nabla f{\left(x_k\right)}^{\text{T}}A\nabla f\left(x_k\right)}{\nabla f{\left(x_k\right)}^{\text{T}}{A}^2\nabla f\left(x_k\right)}$ (2.15)

BB步长是取SD算法或MG算法的上一步步长，在实际计算中，BB算法的数值结果明显优于SD算法和MG算法。BB型算法的迭代过程中，函数值并不严格减小。数值实验表明，BB型算法实际上是一种非单调下降方法，在求解严格凸二次函数时具有优势。

3. 算法介绍

负梯度算法设计较为简单，计算量小，储存变量少，对初始点没有特别要求，许多算法的初始方向都是最速下降方向(即负梯度方向)。由于BB步长没有严格的规定，BB型算法也逐渐增多，接下来将普通的负梯度法和BB型算法两两分组进行介绍。

3.1. 最速下降法和Barzilai-Borwein-1算法

最速下降法是一种最古老的优化算法，它的收敛速度与目标函数的性质有极强相关性，例如矩阵的维数，矩阵的条件数，但其算法简单以目标函数的负梯度方向为搜索方向，具体算法如下：

算法1 (SD算法)：令 $\left\{x_k\right\}$ 为SD算法求解问题(2.1)过程中的迭代序列

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长： ${\alpha }_k=\frac{\nabla f{\left(x_k\right)}^{\text{T}}\nabla f\left(x_k\right)}{\nabla f{\left(x_k\right)}^{\text{T}}A\nabla f\left(x_k\right)}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

SD算法每次迭代的计算量和储存量少，对初始点的要求不高，可以比较快地从初始点到达极小点附近，但在接近极小点时会出现锯齿现象，所以每次迭代移动的步长很小，具有明显的周期性，侧面说明该下降方向是规则出现的，使收敛速度很慢，BB-1算法继承了SD算法的优点同时避免了锯齿现象的产生，由于BB-1步长的特点，函数值并不严格减小，但收敛速度快和迭代次数少，在求解严格凸二次函数时具有优势。

算法2 (BB-1算法)：令 $\left\{x_k\right\}$ 为BB-1算法求解问题(2.1)过程中的迭代序列，

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长： ${\alpha }_k=\frac{s_{k-1}^{\text{T}}{s}_{k-1}}{s_{k-1}{y}_{k-1}}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-{\alpha }_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

3.2. 最小梯度法和Barzilai-Borwein-2算法

最小梯度法(MG)是在SD算法的基础上使函数值 $f\left(x\right)$ 沿着射线 $\left\{x_k-{\alpha }_k\nabla f\left(x_k\right):\alpha >0\right\}$ 最小化，一定程度上加速了收敛速度，减少了迭代次数，但同样会在接近极小点时出现锯齿现象，而BB-2算法继承了MG算法优点的同时，避免了锯齿现象加速了收敛速度，减少了迭代次数和迭代时间。

算法3 (MG算法)：令 $\left\{x_k\right\}$ 为MG算法求解问题(2.1)过程中的迭代序列

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长： ${\alpha }_k=\frac{\nabla f{\left(x_k\right)}^{\text{T}}A\nabla f\left(x_k\right)}{\nabla f{\left(x_k\right)}^{\text{T}}{A}^2\nabla f\left(x_k\right)}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

算法4 (BB-2算法)：令 $\left\{x_k\right\}$ 为BB-2算法求解问题(2.1)过程中的迭代序列，

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长： ${\alpha }_k=\frac{s_{k-1}^{\text{T}}{y}_{k-1}}{y_{k-1}^{\text{T}}{y}_{k-1}}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

3.3. 交替最小化梯度法和交替梯度法

交替最小化梯度法(AM)是交替使用步长 ${\alpha }_k^{SD}$ 和 ${\alpha }_k^{MG}$，受矩阵条件数的影响较小，交替梯度法(AS)是在经典BB算法的基础上，交替使用步长 ${\alpha }_k^{SD}$ 和 ${\alpha }_k^{BB1}$，这两种算法在接近极小点时不会出现锯齿现象，在求解大规模问题时具有优势。

算法5 (AM算法)：令 $\left\{x_k\right\}$ 为AM算法求解问题(2.1)过程中的迭代序列，

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长：当k为奇数时 ${\alpha }_k=\frac{\nabla f{\left(x_k\right)}^{\text{T}}\nabla f\left(x_k\right)}{\nabla f{\left(x_k\right)}^{\text{T}}A\nabla f\left(x_k\right)}$，当k为偶数时 ${\alpha }_k=\frac{\nabla f{\left(x_k\right)}^{\text{T}}A\nabla f\left(x_k\right)}{\nabla f{\left(x_k\right)}^{\text{T}}{A}^2\nabla f\left(x_k\right)}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

算法6 (AS算法)：令 $\left\{x_k\right\}$ 为AS算法求解问题(2.1)过程中的迭代序列，

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长：当k为奇数时 ${\alpha }_k=\frac{\nabla f{\left(x_k\right)}^{\text{T}}\nabla f\left(x_k\right)}{\nabla f{\left(x_k\right)}^{\text{T}}A\nabla f\left(x_k\right)}$，当k为偶数时 ${\alpha }_k=\frac{s_{k-1}^{\text{T}}{s}_{k-1}}{s_{k-1}{y}_{k-1}}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

3.4. 预处理SD算法和预处理BB算法

预处理SD算法结合了SD算法和MG算法的优点，对两者步长进行判选择，从而使迭代次数减少加快函数下降，选择不同的 $\kappa ,\delta \in \left(0,1\right)$，迭代次数不同。预处理BB算法是在预处理最速下降法(ASD)的基础上提出的，它结合了BB-1算法和BB-2算法的优点，对两者步长进行判选择，从而使迭代次数减少加快函数下降，选择不同的 $\mu \in \left(0,1\right)$，迭代次数不同，为解决大规模问题提供选择。

算法7 (ASD算法)：令 $\left\{x_k\right\}$ 为ASD算法求解问题(2.1)过程中的迭代序列，

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$， $\kappa ,\delta \in \left(0,1\right)$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长：若 ${\alpha }_k^{MG}/{\alpha }_k^{SD}>\kappa$， ${\alpha }_k={\alpha }_k^{MG}$，否则 ${\alpha }_k={\alpha }_k^{SD}-\delta {\alpha }_k^{MG}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

算法8 (ABB算法)：令 $\left\{x_k\right\}$ 为ABB算法求解问题(2.1)过程中的迭代序列，

步骤1初始化参数： $x_0\in {\Re }^n$，误差 $\epsilon$， $k=1$，最大迭代次数 $iMax$，初始步长 $a_1$， $\mu \in \left(0,1\right)$；

步骤2收敛性检验：若 $\Vert \nabla f\left(x_k\right)\Vert \le \epsilon$，输出 $x_k$ 作为近似的数值解；

步骤3确定下降搜索方向：计算 $d_k=-\nabla f\left(x_k\right)$；

步骤4选取步长： ${\alpha }_k^{BB2}/{\alpha }_k^{BB1}<\mu$， ${\alpha }_k={\alpha }_k^{BB2}$，否则 ${\alpha }_k={\alpha }_k^{BB1}$；

步骤5定义下一步迭代：取 $x_{k+1}=x_k-a_k\nabla f\left(x_k\right)$， $k=k+1$ 转步骤2。

此外还有很多关于BB步长的研究例如使 ${\alpha }_k={\alpha }_k^{NBB}=\sqrt{{\alpha }_k^{BB1}{\alpha }_k^{BB2}}$ 的新BB [13] 算法、在循环BB算法

(CBB)基础上使 ${\alpha }_k={\alpha }_k^{CABB}\{\begin{array}{l}{\alpha }_k^{BB2}{\alpha }_k^{BB2}/{\alpha }_k^{BB1}<\kappa \\ {\alpha }_k^{CBB}\end{array}$ 的自适应循环BB [8] (CABB)算法、令

${\alpha }_k^{stab}=\frac{\Vert x_{k+1}-x_k\Vert }{\Vert -\nabla f\left(x_k\right)\Vert }$ 使 ${\alpha }_k=\min \left\{{\alpha }_k^{BB},{\alpha }_k^{stab}\right\}$ 的BBstab [9] 算法，这些都是在经典BB算法的基础上优化BB

步长进而产生的新算法，这些都是在改变迭代步长，但数值研究表明，初始 ${\alpha }_1$ 的选取可以影响算法的迭代次数和运行时间，选取初始步长的方法如下：

1) 采用任一种一维寻优法，此时 ${\alpha }_k=\arg \underset{{\alpha }_k>0}{\min }f\left(x_k-\alpha \nabla f\left(x_k\right)\right)$ 中 $f\left(x_k-\alpha \nabla f\left(x_k\right)\right)$ 是 $\alpha$ 唯一元函数，利用任一种一维寻优都可以求得 ${\alpha }_1$。

2) 微分法，由 $\alpha f\left(x_k-\alpha \nabla f\left(x_k\right)\right)=\phi \left(\alpha \right)$ 对于一些简单的情况可以直接令 ${\phi }^{\prime }\left(\alpha \right)=0$ 求出近似的最优步长 ${\alpha }_1$ 的值。

3) 直接赋值，可以直接令 ${\alpha }_1=1$。

4) 选取Hessian矩阵最小或最大特征值的倒数 $\frac{1}{\lambda \min }$ 或 $\frac{1}{\lambda \max }$。

利用上述介绍的算法解决不同维数的严格凸二次函数，同时利用上述方法选取初始步长 ${\alpha }_1$ 进行数值实验，观察算法产生的迭代次数、迭代时间、函数值的变化。

4. 数值实验与比较

本节通过上述八种优化算法求解(2.1)进行数值实验，为了避免偶然性造成的误差，随机生成(0, 100)内的2、4、10、20、30个正整数作为 $\left\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\right\}$ 令(2.1)中 $A=diag\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\right)$ 和 $b=e_n$，选取不同的初始步长 ${\alpha }_1$ 观察迭代次数、迭代时间。设置相关参数误差 $\epsilon ={10}^{-8}$、 $iMax=10000$、 $\kappa =0.5$、 $\delta =0.5$、 $\mu =0.5$、 $x_1=0$。 $A_1=diag\left(30,2\right)$、 $b_1=e_2$； $A_2=diag\left(82,89,34,71\right)$、 $b_2=e_4$； $A_3=diag\left(89,56,9,69,95,5,97,13,61,86\right)$、 $b_3=e_{10}$； $A_4=diag\left(80,61,25,37,53,21,92,37,5,52,60,64,34,45,75,38,61,99,61,88\right)$、 $b_4=e_{20}$； $A_5=diag(13,9,20,11,19,50,99,98,76,71,17,21,28,23,20,53,48,48,18,76,63,27,67,73,1,21,59,67,60,60)$、 $b_5=e_{30}$；求得 $A_1$、 $A_2$、 $A_3$、 $A_4$、 $A_5$ 的条件数分别为15、2.62、19.4、19.8、99。

本文所有实验在Windows操作系统(主频2.59 GHz的64位CPU，运行内存8 GB)平台上MatlabR2018b

软件和Jupyter Notebook (py34)的环境中进行。方法一取初始步长 ${\alpha }_1=\frac{\nabla f{\left(x_1\right)}^{\text{T}}\nabla f\left(x_1\right)}{\nabla f{\left(x_1\right)}^{\text{T}}A\nabla f\left(x_1\right)}$，方法二取初始步长 ${\alpha }_1=1$，方法三取初始步长 ${\alpha }_1=\frac{1}{{\lambda }_{\min }}$，方法四取初始步长 ${\alpha }_1=\frac{1}{{\lambda }_{\max }}$。利用python语言编写程序整理出八种算法选取不同初始步长的迭代次数，如表1所示：

Table 1. The number of iterations of 8 algorithms

表1. 8种算法的迭代次数

整理出程序运行所需要的时间，为了更方便地观察将时间扩大1000倍，如表2所示：

Table 2. Iteration time of 8 algorithms

表2. 8种算法的迭代时间

将这八种算法的迭代次数绘图，如图1~8所示：

Figure 1. Gradient descent

图1. 最速下降法

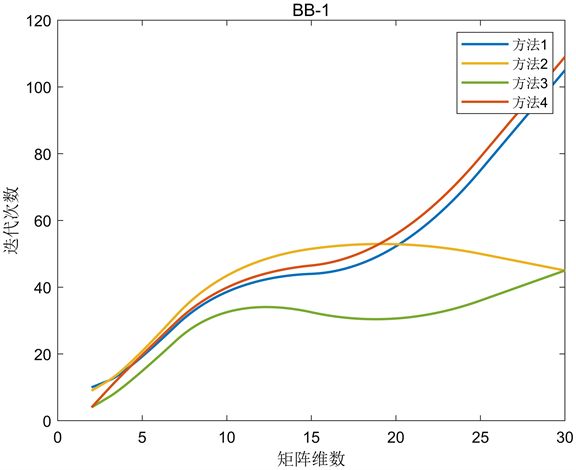
Figure 2. Barzilai-Borwein-1 algorithm

图2. Barzilai-Borwein-1算法

Figure 3. Minimum gradient method

图3. 最小梯度法

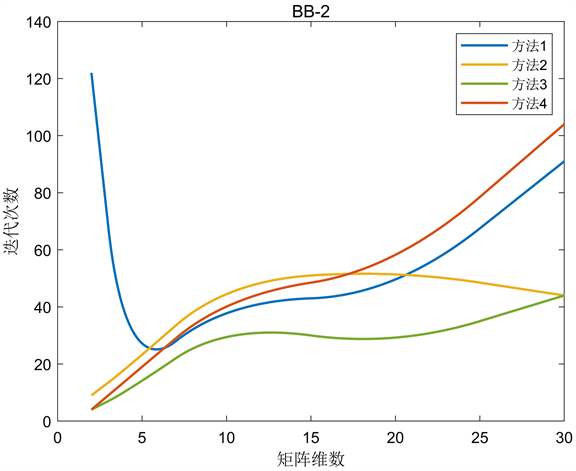
Figure 4. Barzilai-Borwein-2 algorithm

图4. Barzilai-Borwein-2算法

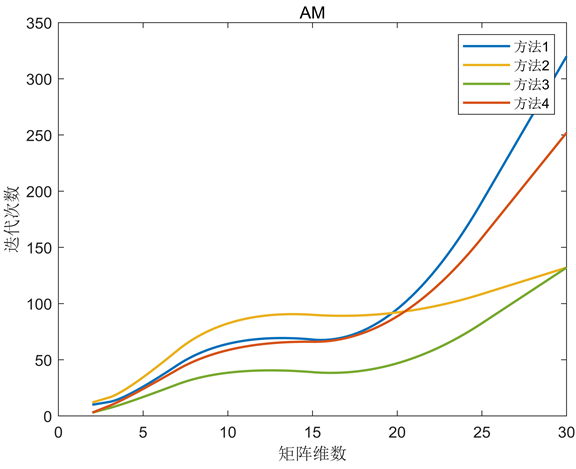
Figure 5. Alternating minimization gradient method

图5. 交替最小化梯度法

Figure 6. Alternating gradient method

图6. 交替梯度法

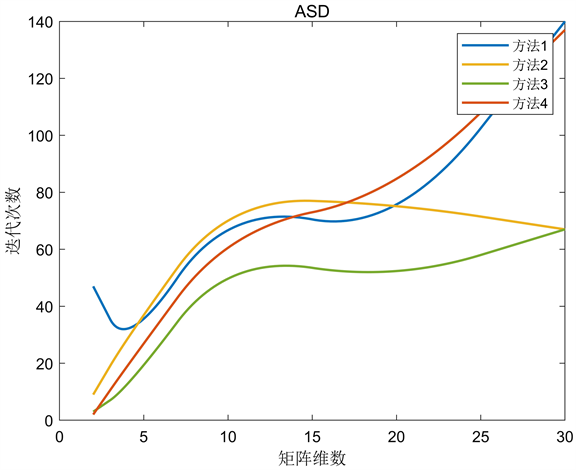
Figure 7. The fastest descent method of pretreatment

图7. 预处理最速下降法

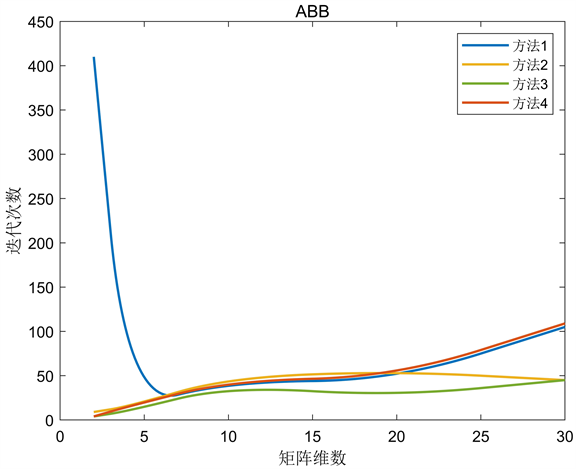
Figure 8. Preprocessing Barzilai-Borwein algorithm

图8. 预处理Barzilai-Borwein算法

从图中可以看出，条件数对一般的负梯度算法影响较大，而BB算法更稳定，在解决大规模问题时更有竞争力。BB-1与BB-2算法相比，后者在矩阵维数较小时没有明显的优势，但随着矩阵维数的增加差距逐渐减小，甚至有稍微的优势。ASD算法对步长进行了选择，迭代次数大大减少，且当矩阵条件数越大其优势越发明显。ABB算法对BB步长进行了选择，实验结果表明，当矩阵维数较小时，ABB算法更接近BB-2算法；当矩阵维数较大时，ABB算法更接近BB-1算法。BB型算法比一般的负梯度算法更复杂，计算和存储的变量更多，但在运行时间上仍占优势。实验数据表明初始步长选择方法一和方法四的效果相似，方法三的效果最好，特别是当矩阵的维数和条件数越大时越有优势，这也反映出选择合适的初始步长可以改变算法的效果。

5. 负梯度算法的应用

负梯度算法广泛应用于图像重建 [14]、超分辨率图像技术 [15]、文本识别等大规模问题。其中图像重建的方法主要分为两类：第一种是直接利用数学反计算求横截剖面，称为解析图像重建；第二种是一系列的区域迭代，称为迭代图像重建。迭代法能够充分利用系数的稀疏性，具有占用内存少、程序设计简单、无误差积累等优点，图像重建的求解方案：

步骤1：将需要重建的图像放入直角网格，利用发射源和探测器进行扫描。

步骤2：将每个像素按照扫描次序排列，第j个像素中 $x_j$ 表示射线吸收系数， $x_j$ 为常数，第j个像素与第i条射线相交的长度用 ${\alpha }_{ij}$ 表示， ${\alpha }_{ij}$ 代表第j个像素沿第i条射线的贡献值，用 $y_i$ 性表示沿第i方

条射线方向的总吸收值，写成线性方程 $y_i={\displaystyle \underset{j=1}{\overset{N}{\sum }}{\alpha }_{ij}{x}_j},i=1,2,\cdots ,N$。

步骤3：将线性方程组写成矩阵形式 $AX=Y$，其中 $X,Y$ 都是向量A是投影矩阵。

步骤4：将 $AX=Y$ 转化为极小化问题 $\min f\left(x\right)={\Vert AX-Y\Vert }_2^2$。

步骤5：利用负梯度算法求解极小化目标函数 $f\left(x\right)$。对CT (Computed tomography)图9进行图像重建，结果如图10所示：

Figure 9. The original image

图9. 原图像

Figure 10. The processed image

图10. 处理后的图像

可以看出，经过处理的图像显示了原图像中不容易观察到的地方。虽然图像有一定的分辨率，但仍然不够清晰。超分辨率图像技术是通过优化算法将低分辨率图像转化为高分辨率图像。高分辨率图像具有较高的像素密度，使图像质量更细腻、更自然、纹理更清晰，这是图像增强领域中一个非常重要的问题。传统的超分辨率技术通常采用负梯度算法求解，求解方案如下：

步骤1：假设模型，一般假设超分辨率模型为 $Y_k=D_k{H}_k{F}_{k}X+V_k,k=1,2,\cdots ,N$，其中向量X表示待求的高分辨率图像；向量 $Y_k$ 表示所观察的低分辨率图像； $D_k,F_k,H_k$ 分别表示下采样矩阵、模糊矩阵、运动矩阵； $V_k$ 表示附加的高斯噪声。

步骤2：在超分辨率模型中将这些估计量的定义重写为最小化问题

$\hat{X}=\underset{X}{\arg \min }\left[{\displaystyle \underset{k=1}{\overset{N}{\sum }}\rho \left(Y_k,D_k{H}_k{F}_{k}X\right)}\right],k=1,2,\cdots ,N$，其中 $\rho$ 为模型和测量值之间的“距离”，令 $D_k{H}_k{F}_k=W_k,k=1,2,\cdots ,N$，当 $\rho$ 是残差的二范数时可以得到最小二乘方程 $\hat{X}=\underset{X}{\arg \min }\left[{\displaystyle \underset{k=1}{\overset{N}{\sum }}{\Vert W_{k}X-Y_k\Vert }_2^2}\right],k=1,2,\cdots ,N$。

步骤3：为了避免因低分辨率图像提供数据不足而造成的伪影，引入正则化项 $\lambda J\left(X\right)$，那么问题将

改写为 $\hat{X}=\underset{X}{\arg \min }\left[{\displaystyle \underset{k=1}{\overset{N}{\sum }}{\Vert W_{k}X-Y_k\Vert }_2^2}+\lambda J\left(X\right)\right],k=1,2,\cdots ,N$，令 ${\displaystyle \underset{k=1}{\overset{N}{\sum }}{\Vert W_{k}X-Y_k\Vert }_2^2}=E_{\rho }\left(X\right)$ 可以写成 $\hat{X}=\underset{X}{\arg \min }f\left(X\right)=\underset{X}{\arg \min }\left\{E_{\rho }\left(X\right)+\lambda J\left(X\right)\right\}$。

步骤4：利用负梯度算法求解极小化目标函数 $f\left(X\right)$。对低分辨率图11使用超分辨率技术，结果如图12所示：

Figure 11. The original image

图11. 原图像

Figure 12. The processed image

图12. 处理后的图像

原图像的分辨率为：250 × 250而处理后的图像为：434 × 363，不仅如此，图像的大小也从40.6 KB减小到了11.7 KB。超分辨率技术不仅提高了图像的分辨率，还减少了图像占用的内存。虽然图像的分辨率有所提高，但如何捕捉图像中的文字信息呢？字符识别技术适用于纸张打印、图片等字符的识别，识别结果以文本的形式存储在计算机中，如车牌识别就可以将优化算法和BP神经网络结合，可以选择负梯度算法来寻找最优的连接权值，这样可以提高字符识别算法的准确率，达到预期的效果。

最优化问题在深度学习中占有非常重要的地位，很多深度学习模型最终都会归结为求解最优化问题，求解大规模最优化问题通常采用数值计算方法，而负梯度算法就是最经典的数值计算方法，具有存储容量小，结构简单，易于实现的优点，是最简便也是最常用的优化算法之一，在训练类算法中，负梯度算法通常用于求解极小化问题。在现实生活中，需要根据不同的数据选择合适的负梯度算法，以降低计算成本，提高算法的整体效率。

6. 结论与期望

随着计算机技术和算法语言的快速发展，各种优化算法不断被提出，为解决大规模问题提供了新的选择。本文对八种负梯度算法进行了讨论和比较。同时，将这些算法用于解决不同维数的严格凸二次函数。通过对比实验数据，发现BB型算法在迭代次数和迭代时间上都比一般的负梯度算法更有优势，并且矩阵的条件数越大优势越大。在数值实验中，发现选择不同的初始步长会产生不同的效果，通过比较发现Hessian矩阵最小特征值的倒数是最佳选择。最后，介绍了负梯度算法在图像重建、超分辨率图像技术、文本识别中的应用。

由于BB步长没有严格的规定，新的BB型算法不断被提出，理论知识不断被完善，它们在解决特殊问题时具有或多或少的优势。许多书籍在介绍优化算法时对BB型算法的介绍较为笼统，网上关于BB型算法的语言代码也不多，大家对BB型算法只有一个大概的印象，希望通过本文大家对BB型算法的发展、理论知识、特点有一个详细的认识。本文推广了BB型算法，为BB型算法的进一步研究提供了参考，后续将会对BB步长和共轭梯度进行研究，结合两者的优点设计出一种新的BB型算法。