1. 引言
局域量子不确定性(LQU)是表征量子关联的一种重要度量方式,在量子信息处理中发挥了不可或缺的作用 [1]。近年来,量子关联中LQU的研究引起了人们极大兴趣。Girolami等人 [2] 在Skew信息的基础上首次提出了用LQU表征量子关联。Slaoui等人 [3] 研究了在各向异性及各向同性均匀外磁场作用下,海森堡自旋链XY模型的LQU量子关联特性,结果表明LQU与局域量子Fisher信息具有相似的变化,且外磁场的增加可以增强系统的量子关联。Ali等人 [4] 将二比特量子系统LQU推广到多比特情形,并证明其适用于N比特的任意初始量子态。曹蕾等人 [5] 研究了LQU在(1/2, 1)混合自旋XY链中随着磁场的变化趋势,发现在高温或测量某些物理量情况下,使用LQU表征系统量子关联比Negativity或Quantum discord更具优势。相对于Quantum discord,LQU在计算过程中只需要找到3*3对称矩阵的最大特征值,从而极大地简化了计算任务。除此之外,LQU还为固态多体自旋链系统的量子临界性检验、开放量子系统的非马尔科夫效应提供了新的方法 [6] [7] [8]。
另一方面,腔光力学系统在光力相互作用下可以产生许多奇特的量子效应,如光力学纠缠、光力诱导透明、振子基态冷却和压缩态制备等,已经广泛应用于量子冷却、量子精密测量和量子信息处理等诸多领域 [9]。然而,迄今为止很少有学者关注腔光力学系统中的LQU量子关联的特性研究。本文,我们研究了相位阻尼噪声环境中复合腔光力学系统两原子间LQU的调控,对有效利用腔光力学系统的腔场参数实现LQU量子关联调控具有重要的意义。
本文结构如下:第二节建立复合腔光力学系统模型;第三节讨论局域量子不确定性;第四节为数值结果与分析;第五节为本文总结。
2. 系统模型
我们考虑由一个J-C模型和一个原子腔光力学系统构成的复合腔光力学系统,即两个二能级原子分别置于单模光腔和含机械谐振子光腔中,并且考虑含机械谐振子光腔中的Kerr非线性效应与光子数Stark位移效应,如图1所示。此时,复合腔光力系统的总哈密顿量可以表示为 [10]:
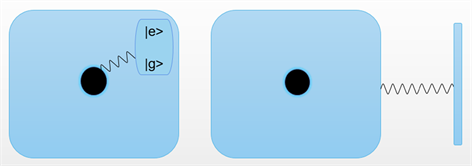
Figure 1. The schematic diagram of the composite cavity optomechanical system
图1. 复合腔光力系统示意图
(1)
上式中,第一项描述了J-C模型子系统中原子与腔场之间的两体相互作用,第二项描述了腔光力学子系统中原子、腔场以及振动镜之间的三体相互作用,第三项和第四项分别表示腔光力学子系统中Kerr非线性效应以及光子数依赖Stark位移效应。其中,算符
和
分别表示第i个原子的上升和下降算符,
和
分别表示第i个单模腔场的产生算符和湮灭算符,
和
是原子腔光力系统中振动镜的产生和湮灭算符,
表示单模光场子系统中原子–腔场(J-C模型)耦合系数,
表示腔光力学子系统中原子–腔场(含振动镜)耦合系数,G表示腔光力学子系统中腔场和振动镜之间的耦合系数,
是腔光力学子系统中振动镜的频率。
为简便计算,令
,
,
,取普朗克常数
,则上述哈密顿量可改写为:
(2)
考虑两原子初始处于激发态
和基态
的任意纠缠态,则两原子系统的初态为:
(3)
其中,
表示原子初态的相干角,满足
。假设机械谐振子初始处于真空态
,J-C模型子系统中的腔场初始处于真空态
,腔光力学子系统中的腔场处于单光子态
,那么,整个系统的初态描述如下:
(4)
在哈密顿量
的作用下,整个系统随时间演化的态矢量为:
(5)
将(5)式及系统哈密顿量代入薛定谔方程:
(6)
考虑整个系统的初值条件为:
(7)
利用给定条件进一步求解可得出系数:
(8)
其中,
,
,
。由此,将上述结果代入方程(5)中,利用系统的密度矩阵
,两个二能级原子的约化密度矩阵
可以根据公式
进行求解,即对系统中的两个腔场及振动镜求偏迹,则两个二能级原子的密度算符为:
(9)
在标准基
,
,
,
下,此复合腔光力系统中两个二能级原子的约化密度矩阵可表示为:
(10)
其中,
和
分别表示
和
的复共轭运算。
在实际环境中,复合腔光力学系统由于受到外部噪声环境的影响,导致量子态发生退相干效应。其中,典型的退相干效应模型可以用相位阻尼通道表示:
(11)
上式中,
表示描述单个量子比特的退相干过程的Kraus算子。相位阻尼通道作用的Kraus算符表示为:
(12)
其中,参数
表示量子态衰变的概率并满足
,且
表示相位阻尼通道中的相位衰减因子,
的取值范围为
,则参数
的取值范围为
,Kraus算符需要满足归一化条件
。
利用(10)~(12)式进行计算,即可求出相位阻尼噪声环境下复合腔光力学系统中两原子随时演化的约化密度矩阵。
3. 局部量子不确定性与量子纠缠
基于量子系统的局域测量理论,Girolami等人在Skew信息 [11] 的基础上提出的一种新的量子关联的表征方式。对于
维希尔伯特空间中两体系统量子态
,LQU表达式为:
(13)
其中,
是表示量子态
和算子
之间的非交换的Skew信息,该信息的最小值是通过对A系统所有局域投影测量算符
的优化求解得出,已经证明LQU满足量子关联特性度量的所有物理要求,且是
维希尔伯特空间中两体量子系统中可靠的量子相关度量。由于LQU要在优化后具有解析解,所以通过LQU来定量分析量子关联是有一定的优势的,对于任意
维两体系统,LQU表达式改写为:
(14)
其中
代表矩阵W的最大特征值,矩阵W是一个3 × 3的对称矩阵,每个矩阵元素的定义式为:
(15)
上式中,
和
代表泡利矩阵,i,j分别可取1,2,3,
表示子系统B的单位矩阵。特别地,对于2 × 2维希尔伯特空间中两体量子系统,X型量子态是一种重要的两量子比特态,在标准计算基矢下,X型量子态密度矩阵为:
(16)
在布洛赫球表示中,该密度矩阵
也可写为
(17)
其中,
(
)。通过计算,对称矩阵W的矩阵元可以写为:
(18)
其中,
是密度矩阵
的本征值。
为了对比分析复合腔光力学系统中两二能级原子的局域量子不确定性与量子纠缠两者之间的差异,我们引入共生纠缠(Concurrence)来度量两原子间的纠缠度。对于X型的密度矩阵,共生纠缠的表达式可以写为:
(19)
接下来,我们通过数值计算,讨论了相位阻尼参数
、原子–腔场(J-C模型)耦合系数
、原子–腔场(含振动镜)耦合系数
、腔场–振动镜耦合系数G对复合腔光力学系统中LQU的影响。
4. 数值结果与分析
4.1. 复合腔光力学系统的相位阻尼参数对LQU的影响
在复合腔光力学系统中,分析相位阻尼参数对两原子间量子关联LQU的影响。对(10)~(12)式进行数值计算,并作出图2,其中
,
,相位阻尼参数
,
,
分别对应实线、点划线和点线。当两原子初始处于最大纠缠态时,LQU随时间演化呈现出从振荡衰减到振荡增加的周期交替性变化规律,由数值计算可知,其振荡周期为17π。随着相位阻尼参数 的增加,两原子LQU的衰减速率增加,表明复合腔光力学系统中两个原子间LQU的值随相位阻尼增强而逐渐衰减。产生这一现象的物理本质是环境噪声诱导了原子间量子关联的退相干。
为了对比分析复合腔光力学系统中两原子间LQU与Concurrence的差异,我们探讨相位阻尼参数对两原子间量子纠缠Concurrence的影响。对(19)式进行数值计算,并作出图3,其中
,
,相位阻尼参数
,
,
分别对应实线、点划线和点线。当两原子初始处于最大纠缠态时,两原子的Concurrence随时间演化呈现出周期性交替振荡的变化规律,且振荡周期不发生改变。观察图3中三条曲线,发现当环境的相位阻尼参数增大时,两原子间的量子纠缠减小,且有纠缠突然死亡现象的发生,Concurrence演化的振荡频率加快。对比图2和图3发现,两原子间LQU的下降速度比Concurrence慢,表明LQU对环境噪声的影响更具有鲁棒性。并且,当环境噪声较大时,两原子间量子关联LQU明显高于量子纠缠Concurrence,说明在相同初始条件下,两原子间量子关联的量子态呈现明显的强弱分级关系。特别地,在某个时间段内,由于相位阻尼参数的影响使得系统中两原子的量子纠缠完全消失,而两原子的LQU量子关联却依然存在。因此,在开放系统中,LQU更适合度量量子系统的非经典关联。
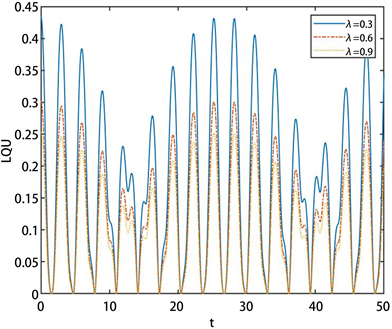
Figure 2. The effect of dephasing parameters on LQU of two atomsin the composite cavity optomechanical system, where
,
, and the dephasing parameters
correspond to the solid, dotted and dashed lines respectively
图2. 复合腔光力学系统中相位阻尼参数对两原子间LQU的影响,其中
,
,相位阻尼参数
分别对应实线、点划线和点线

Figure 3. The effect of dephasing parameters on Concurrence of two atoms in the composite cavity optomechanical system, where
,
, the dephasing parameters
correspond to the solid, dotted and dashed lines respectively
图3. 复合腔光力学系统中相位阻尼参数对两原子间Concurrence的影响,其中
,
,相位阻尼参数
分别对应实线、点划线和点线
4.2. 相位阻尼噪声环境下复合腔光力学系统的量子关联调控
图4表示复合腔光力学系统中原子–腔场(J-C模型)耦合系数
、原子–腔场(含振动镜)耦合系数
对两原子间LQU的量子关联调控,其中
,
,耦合系数
,
分别对应实线与点划线。当耦合系数
和
同时发生改变时,两原子间的量子关联LQU的振荡幅度和振荡周期均发生改变。随着耦合系数
和
的同时增大,LQU平均振荡幅度变大,振荡频率明显加快,振荡周期变短,并且从不规则振荡转变为规则的等幅振荡过程。上述现象说明通过共同改变原子–腔场(J-C模型)耦合系数和原子–腔场(含振动镜)耦合系数,能够调控复合腔光力学系统中两原子态的量子关联强度和演化周期,从而实现量子系统的局域不确定性关联的增强。

Figure 4. The controlling of the atom-cavityfield (J-C model) coupling
and the atom-cavityfield (with vibrating mirror) coupling
on the LQU of two atoms in the composite cavity optomechanical system, where
,
,
and
correspond to the solid and dotted lines respectively
图4. 复合腔光力学系统中原子–腔场(J-C模型)耦合系数
和原子–腔场(含振动镜)耦合系数
对两原子间LQU的调控,其中
,
,
和
分别对应实线与点划线
图5表示在某一时刻参数下复合腔光力学系统中原子–腔场(含振动镜)耦合系数
对两原子LQU的量子关联调控,其中
,
,
,
。复合腔光力学系统两原子间的量子关联LQU随着原子–腔场(含振动镜)耦合系数
的增大呈现先增大而后逐渐振荡递减,最后逐渐稳定在某一数值进行振荡变化的行为趋势,说明通过改变原子–腔场(含振动镜)耦合系数
,也能够调控复合腔光力学系统中两原子态的量子关联强度,从而实现量子系统的局域量子不确定性的关联增强。
图6表示在某一时刻参数下复合腔光力学系统中振动镜–腔场耦合系数G对两原子LQU的量子关联调控,其中
,
,
,
。随着耦合系数G的增大,两原子间的量子关联LQU呈现出与图5相似的变化规律。表明振动镜–腔场耦合系数G也能够对复合腔光力学系统中两原子间的量子关联强度进行调控,但其调控能力弱于原子–腔场(含振动镜)耦合系数
。
图7表示在某一时刻参数下复合腔光力学系统中原子–腔场(J-C模型)耦合系数
对两原子LQU的量子关联调控,其中
,
,
,
。随着原子–腔场(J-C模型)耦合系数的增大,两

Figure 5. The controlling of the atom-cavityfield (with vibrating mirror) coupling
on the LQU of two atoms in the composite cavity optomechanical system, where
,
,
,
图5. 复合腔光力学系统中原子–腔场(含振动镜)耦合系数
对两原子间LQU的调控,其中
,
,
,
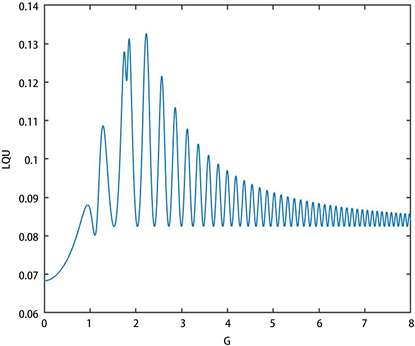
Figure 6. The controlling of the vibrating mirror-cavityfield coupling G on the LQU of two atoms in the composite cavity optomechanical system, where
,
,
,
图6. 复合腔光力学系统中振动镜–腔场耦合系数G对两原子间LQU的调控,其中
,
,
,
原子间的LQU随耦合系数
的增大呈现交替的等幅振荡现象,表明单独增大原子–腔场(J-C模型)耦合系数不能有效提高对复合腔光力学系统中两原子态的量子关联。
对比分析图5、图6和图7发现,随着原子–腔场(含振动镜)耦合系数
以及振动镜–腔场耦合参数G的增大,两原子间LQU的振荡次数增加,导致振荡周期缩短,而原子–腔场(J-C模型)耦合系数
的增大并不影响两原子间LQU的振荡周期。表明相位阻尼环境下复合腔光力学系统中两原子之间的振荡周期由原子–腔场(含振动镜)耦合系数
以及振动镜–腔场耦合参数G决定。
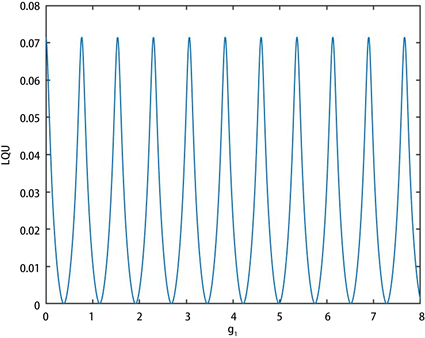
Figure 7. The controlling of the atom-cavityfield (J-C model) coupling
on the LQU of two atoms in the composite cavity optomechanical system, where
,
,
,
图7. 复合腔光力学系统中原子–腔场(J-C模型)耦合系数
对两原子LQU的量子关联调控,其中
,
,
,
5. 结论
本文利用量子关联的相关理论,研究了相位阻尼对复合腔光力学系统中局域量子不确定性的影响,分析了复合腔光力学系统中各项参数对相位阻尼环境中两原子间LQU的调控作用。结果表明:随相位阻尼参数的增强,复合腔光力学系统中两个原子间LQU和Concurrence的衰减速率逐渐增加,并且LQU的衰减速度比Concurrence慢,当相位阻尼参数很大时,复合腔光力学系统中量子纠缠消失但仍存在量子关联LQU,表明相位阻尼环境能够诱导系统产生退相干效应,且LQU相比于Concurrence更适合表征复合腔光力学系统中的量子关联。通过改变原子–腔场(J-C模型)耦合系数、原子–腔场(含振动镜)耦合系数和振动镜–腔场耦合系数等参数,能够调控两原子间LQU。特别地,当改变原子–腔场(含振动镜)耦合系数、振动镜–腔场耦合系数,或者同时改变原子–腔场(J-C模型)耦合系数和原子–腔场(含振动镜)耦合系数时,可以实现复合腔光力学系统两原子间量子关联的增强。此外,通过选择腔光力学系统中振动镜–腔场耦合系数和原子–腔场(含振动镜)耦合系数可以实现对LQU演化周期的调控。因此,在相位阻尼环境中,复合腔光力学系统的各项参数对LQU具有明显的调控作用,为实现原子腔光力学系统的纠缠操纵、量子关联增强或保持提供了新的物理方法。
致谢
本论文在周清平教授指导下完成。在这里,首先要感谢恩师在学习过程中的多次指导,并给予我前进的动力,在老师的带领下,积极地投入到学习中,仔细阅读文献,严格推导公式,正是周老师孜孜不倦的教诲,帮我指引科研道路上行进的方向!使我感受到一位研究学者渊博的知识以及认真严谨的学术态度,是我今后学习的榜样和标杆!同时也要感谢导师在我学业以及生活上的帮助和支持。
其次,要感谢本课题组成员以及各位师兄师姐在我学习的道路中提供的交流与帮助,极大的提高了学习效率。同时,感谢学校为学生提供了良好的住宿条件以及优美的生活环境,设立有专门的研究生自习室,为我们创造了良好的学习平台。
最后,向百忙之中审阅我论文的专家表示深深的敬意与感谢。
基金项目
本项目得到国家自然科学基金(11464015,12064012),湖南省自然科学基金(20JJ4496)和吉首大学校级科研课题(Jdy20037)的资助。