基于最大信息系数的用户光伏出力分解技术

Maximal Information Coefficient Based Residential Photovoltaic Power Generation Disaggregation

摘要: 近年来，分布式光伏系统(Distribution Photovoltaic Systems, DPVSs)由于相关政策的支持、低安装成本和易操作性，得到了越来越多用户的青睐。然而大量小于10 kWp的小规模DPVSs是安装于表后侧(Behind-the-Meter, BTM)的，光伏发电信息并未被单独计量，这导致了光伏发电对表前侧(配电网侧)的不可见性。若配网侧仅以净负荷数据进行能量管理，将无法进行最优的配电网调度和需求响应策略的实施，导致一系列的安全经济问题。为解决上述问题，本文提出了一种针对小规模DPVS的BTM净负荷分解方法，该方法可在不依赖于天气数据和光伏设备物理模型的情况下，对BTM光伏发电进行估计。所提算法在社区用户的DPVS通常表现出近似的光伏发电特性这一假设的情况下，利用邻近用户的净负荷来提取光伏发电信息作为彼此间相互的光伏代理。最终的光伏发电分解结果将根据最大信息系数(Maximal Information Coefficient, MIC)进行确定。实验结果表明，所提分解算法在不依赖气象数据的情况下拥有较高的分解精度。

Abstract: Due to policy support, low cost and easy applicability, distribution photovoltaic systems (DPVSs) are increasingly popular among residential community. However, small-scale DPVSs of less than 10 kWp are always installed behind the meter (BTM), without metering the photovoltaic (PV) power generation separately, which results in the invisible of the PV power generation. Only access of net load data can result in non-optimal distribution network control and optimization, leading to a series of energy management problems. In order to solve the aforementioned problems, this paper proposes a BTM net load disaggregation method focusing on small-scale DPVSs, with only net load data of residential users in a community, without relying on weather data and models assumption. Considering that community users’ DPVSs usually exhibit approximate output characteristics, neighboring net load is used to extract PV power generation information as mutual proxies. After obtaining approximate PV proxy data by subtracting composite power of inter-users, Maximal Information Coefficient (MIC) is performed to obtain final PV power generation disaggregation results. Testing results show that the proposed method achieves considerable disaggregation accuracy in the absence of weather data.

1. 引言

不可再生能源的紧缺和环境恶化问题是推动传统化石燃料能源依赖型电力系统转型的主要因素。目前，冰岛、挪威、哥斯达黎加、巴西和加拿大等国已经分别实现了100%、97%、93%、76%和62%的可再生能源并网 [1]。光伏(Photovoltaic, PV)发电考虑到较低的度电成本，以及可从太阳获得大量的可再生资源的特性，具有巨大的发展前景 [2]。为实现光伏发电的就地消纳，目前大量的小型分布式光伏发电设备(Distributed Photovoltaic Systems, DPVSs)都是安装于用户屋顶的 [3]。根据2019年欧洲太阳能发电(Solar Power Europe 2019)统计报告，屋顶光伏的装机容量大约在44 GW至76.5 GW之间 [4]。然而绝大部分的屋顶光伏系统都是安装于表后侧(Behind-the-meter, BTM)的 [5]，且由于成本问题，并未安装有独立计量能量消耗和光伏发电量的表计，这将导致能量管理难以有效实施、储能设备容量无法合理确定以及继电保护难以正确设定等问题的出现。此外，用户由于电力信息隐私的问题，不愿公开住宅能源信息的细节，也将导致电网运营商由于缺乏实际的负荷消耗和光伏发电信息，难以进行最优能量调度的问题。综上所述，设计一种可用于估计BTM系统下的PV发电量的方法是十分有意义的。

目前有关研究BTM系统下PV发电分解方法的文献，可被划分为基于模型假设的分解方法和基于数据驱动的分解方法。以文献 [6] 和 [7] 为代表的基于模型假设的方法的共同特点是，分解的PV发电量是根据假设的PV系统几何参数和PV出力特性进行求解的，这将导致太阳辐照度与PV发电量之间具有过度的传递一致性。因此，一旦假设PV系统模型与实际情况不一致，对PV发电量的估计误差就会持续存在。

基于数据驱动的分解方法则可以避免由于模型假设不合理所引入的误差，但此类分解方法有更高的外部数据需求(如温度数据、辐照度数据等)。部分数据驱动的方法依赖于能量代理的设置来分解净负荷。如在文献 [8] 中，通过使用支持向量回归(Support Vector Regression, SVR)模型估计待分解用户的PV设备装机容量后，PV发电量的分解结果由所设置的单位容量的PV代理的光伏发电量，乘以估计的装机容量获得。在文献 [9] 中，以在馈线侧单独计量所得的用户群的负荷消耗数据和PV发电数据作为额外特征变量，PV发电量的分解结果通过搭设线性回归模型计算获得。

综上所述，无论所用分解方法是基于模型假设还是基于数据驱动的，若想实现BTM系统下净负荷的分解，必须获得至少一种外部变量用于对待分解的用户PV发电量或负荷消耗量进行推导。对于基于模型假设的方法来说，用于推导的外部变量多为气象数据，而对于数据驱动的方法，用于推导的外部变量多为所设代理的负荷消耗或光伏发电数据。

对于外部变量如气象数据来说，若其数据采集地点与待分解用户的净负荷数据采集地点不一致，将引入时间或地理空间的误差。而对于外部变量如代理站点的光伏发电量或负荷消耗量数据来说，代理站点的假设和代理站点的能量数据采集，将极大增加经济成本和时间成本。上述两点都是不利于BTM光伏发电量分解的实际实施的。因此，本文提出了一种基于数据驱动的方法，在仅使用居民用户的净负荷数据的情况下，对BTM光伏发电量进行分解，以解决使用上述外部变量可能带来的多种问题。

2. BTM光伏发电量分解算法介绍

2.1. 使用社区用户总净负荷筛选PV代理站点

由于处于相同的地理位置，同一社区内的天气条件是相似的，如太阳辐射、环境温度等。因此，太阳能光伏板接受到的单位面积辐照度、工作温度应是近似的，也就意味着整个社区内不同的光伏板的PV发电量曲线的形态是近似的，只是由于装机容量的不同，在幅值上有差异。因此每个用户的光伏设备都可看作是其它用户的PV代理站点。

即使用户间的光伏设备可以作为彼此的PV代理站点，但由于用户均采用净负荷计量的方式，也无法获得实际的光伏发电量信息用作BTM光伏发电量的分解。虽然实际的光伏发电量无法获得，但用户间的光伏发电量差值是有可能获得的。假设两个用户具有近似的负荷消耗量和负荷消耗行为，通过对这两个用户的净负荷作差，以抵消其中的负荷消耗信息，能获得近似的光伏发电量差值，由于用户间光伏设备装机容量不同，所导致的光伏发电量的差值。考虑到辐照度与PV发电量之间的高度的线性关系，此时获得的PV发电量差值曲线的形态，应与社区内其余用户的PV发电量曲线的形态近似。那么该PV发电量差值曲线也可看作一个特殊的PV代理站点的PV发电量结果。

净负荷定义为负荷消耗减去PV发电量，假设一个社区内共有n个用户，则对于用户i，其负荷消耗如下式(1)所示：

$C_{i,t}=D_{i,t}-P_{i,t},i\in n$ (1)

为使用户之间的负荷消耗的幅值尽可能相似，社区中每个用户的净负荷都需要缩放至相同数量级。由于在夜间，光伏发电量为0，根据式(1)可知，此时光伏发电量为D为0，即负荷消耗C与净负荷D在此时相等。为避免缩放时净负荷中光伏发电量带来的影响，各用户的净负荷将根据夜间耗电量进行缩放，如式(2)所示。

${C^{\prime }}_{i,t}=\frac{C_{i,t}}{\frac{1}{m}{\displaystyle \underset{t_1=1}{\overset{m}{\sum }}{C}_{i,t_1}}},i\in n,t_1\in T_{night}$ (2)

式中， $T_{night}$ 表示夜间时段，分子 $\frac{1}{m}{\displaystyle \underset{t_1=1}{\overset{m}{\sum }}{C}_{i,t_1}}$ 表示，夜间的净负荷均值(由于夜间无光伏发电量，与夜间的负

荷消耗均值相等)，m代表夜间时段时刻点的数量。

则经过缩放后，用户i和用户j的净负荷差值如式(3)所示。

${C^{\prime }}_{i,t}-{C^{\prime }}_{j,t}=\left({D^{\prime }}_{i,t}-{D^{\prime }}_{j,t}\right)-\left(P_{i,t}-{P^{\prime }}_{j,t}\right);i\in n,j\in n,i<j$ (3)

为便于表示，将式(3)改写为式(4)。

$\Delta {C^{\prime }}_{ij,t}=\Delta {D^{\prime }}_{ij,t}-\Delta {P^{\prime }}_{ij,t}$ (4)

由于进行了缩放，在假设用户用电行为近似的情况下，式(4)中的负荷消耗差值 $\Delta {D^{\prime }}_{ij,t}$ 可以看作小的噪声。则式(4)可近似改写为：

$\Delta {C^{\prime }}_{ij,t}\approx -\Delta {P^{\prime }}_{ij,t}$ (5)

且由于上文提及的，社区用户间较近的地理距离以及辐照度与PV发电量之间的高度相关性，可认为用户i和用户j在t时刻光伏设备接受到的单位辐照度 $I_{i,t}$ 和 $I_{j,t}$ 满足如下关系：

$I_{i,t}=I_{j,t}$ (6)

设用户PV装机容量 $\alpha$，单位辐照度I和PV发电量P满足以下关系：

$P=\epsilon \cdot \alpha \cdot I$ (7)

式中 $\epsilon$ 为“辐照度-PV发电量”转换系数，假设不同用户的 $\epsilon$ 相等，则式(6)可改写为如下形式：

$\frac{{P^{\prime }}_{i,t}}{{\alpha }_i}=\frac{{P^{\prime }}_{j,t}}{{\alpha }_j}$ (8)

式中， ${\alpha }_i$ 和 ${\alpha }_j$ 分别代表用户i和用户j的PV装机容量。令用户i和用户j间缩放后的PV发电量差值 $\Delta {P^{\prime }}_{ij,t}={P^{\prime }}_{i,t}-{P^{\prime }}_{j,t}$，则根据式(8)可推导得如下式。

${P^{\prime }}_{i,t}={\beta }_{ij}\Delta {P^{\prime }}_{ij,t}$ (9)

${\beta }_{ij}={\alpha }_i/\left({\alpha }_i-{\alpha }_j\right)$, ${\alpha }_i\ne {\alpha }_j$ (10)

从式(8)中可知，PV发电量差值与PV发电量之间有非常强的线性相关性，这也解释了前文所说PV发电量差值与PV发电量之间有近似的曲线形态。对式(9)同除 ${\alpha }_i$ 可得：

$\frac{{P^{\prime }}_{i,t}}{{\alpha }_i}=\frac{{\beta }_{ij}}{{\alpha }_i}\Delta {P^{\prime }}_{ij,t}$ (11)

则 $\Delta {P^{\prime }}_{ij,t}$ 可以看作，装机容量为 $\frac{{\alpha }_i}{{\beta }_{ij}}$ 的PV设备在t时刻的PV发电量，也即是本文所提的PV代理站

点的PV发电量。

式(9)和式(11)解释了为什么PV发电量差值可作为PV代理站点的PV发电量。同样地，对于同一个社区内的不同用户，根据式(4)至式(11)，通过匹配不同用户的净负荷进行相减，可以求得多个PV发电量差值 $\Delta {P^{\prime }}_{ij,t}$ 作为不同PV代理站点的PV发电量。

然而，用户的用电行为是具有多样性的，也即式(4)所提及的负荷消耗差值 $\Delta {D^{\prime }}_{ij,t}$ 造成的小噪声。因此有必要对不同用户匹配所得的净负荷差值 $\Delta {C^{\prime }}_{ij,t}$ 进行筛选，使其具有足够的代表性，以满足式(5)。

对于拥有n个用户的社区，来说用户间的组合模型有 $\left(n^2-n\right)/2$，也即可以获得 $\left(n^2-n\right)/2$ 个净负荷差值 $\Delta {C^{\prime }}_{ij,t}$。本文将以最大信息系数(Maximal Information Coefficient，MIC)从中筛选出最优的 $\Delta {C^{\prime }}_{ij,t}$。MIC

是一种用于分析变量间相关性的方法，MIC数值越大，两个变量间的相关性越高。MIC的计算方法如文献 [10] 所述，此处不再赘述。令 ${C^{\prime }}_{n,t}$ 为社区中n个用户的总净负荷量，通过计算 $\Delta {C^{\prime }}_{ij,t}$ 和总净负荷量 ${C^{\prime }}_{n,t}$ 的MIC系数，选择其中MIC系数最大时所对应的 $\Delta {C^{\prime }}_{ij,t}$ 作为最合适的PV代理站点的PV发电量。式如(12)所示。

$R_1=\arg \underset{i,j}{\max }\text{MIC}\left({C^{\prime }}_{n,t},\Delta {C^{\prime }}_{ij,t}\right)$ (12)

也就是说，所提方法希望找出与总净负荷量 ${C^{\prime }}_{n,t}$ 相关性尽可能高的 $\Delta {C^{\prime }}_{ij,t}$，因为总净负荷量 ${C^{\prime }}_{n,t}$ 中的总PV发电量的曲线形态应与各用户的PV发电量形态一致，如果 $\Delta {C^{\prime }}_{ij,t}$ 中可包含尽可能少的负荷消耗差值 $\Delta {D^{\prime }}_{ij,t}$ 带来的噪声，则净负荷差值 $\Delta {C^{\prime }}_{ij,t}$ 所呈现出的曲线形态将更近似于总净负荷量 ${C^{\prime }}_{n,t}$ 中的总PV发电量的曲线形态。至此，最佳的PV代理站点可通过筛选获得。

2.2. 使用最大信息系数估计用户PV发电量

为便于表示，将筛选所得最佳PV代理站点的PV发电量结果表示为 $\Delta P_t$。由式(9)可知，用户i经缩放后的PV发电量 ${P^{\prime }}_{i,t}$ 可由代理站点的PV发电量 $\Delta P_t$ 乘以转换系数 $\beta$ 获得，如式(13)所示。

${P^{\prime }}_{i,t}={\beta }_i\Delta P_t;i\in n$ (13)

对于式(13)中的系数 ${\beta }_i$，同样可以通过MIC进行参数搜寻获得，如式(14)所示。

$R_2=\arg \underset{{\beta }_i}{\min }\text{MIC}\left({C^{\prime }}_{i,t}+{\beta }_i\Delta P_t,\Delta P_t\right)$ (14)

根据式(1)中净负荷、负荷消耗与光伏发电量之间的关系可知，式中 ${C^{\prime }}_{i,t}+{\beta }_i\Delta P_t$ 可表示在转换系数 ${\beta }_i$ 下估计的用户负荷消耗值。此处需注意，式(14)中，是希望求得MIC最小时的转换系数 ${\beta }_i$。这是因为希望估计所得的用户负荷消耗值 ${C^{\prime }}_{i,t}+{\beta }_i\Delta P_t$，能尽可能不包含光伏发电量信息 $\Delta P_t$，也即两者之间的相关性最小。设定待优化参数 ${\beta }_i$ 最小可取值为 ${\beta }_{i,\min }$，最大可取值为 ${\beta }_{i,\max }$，步长为 $\Delta {\beta }_i$，通过枚举的方式以获得 $R_2$ 取值最小时的 ${\beta }_i$ 值，即为最优转换系数。

最终，用户i的PV发电量分解结果可通过经缩放后的PV发电量 ${P^{\prime }}_{i,t}$，根据式(2)的反缩放获得。如式(15)所示。

${\hat{P}}_{i,t}={P^{\prime }}_{i,t}\cdot \frac{1}{m}{\displaystyle \underset{t_1=1}{\overset{m}{\sum }}{C}_{i,t_1}}$ (15)

所提社区用户PV发电量分解算法的伪代码如下：

3. 算例分析

3.1. 数据集及评价指标

为验证所提BTM系统下光伏发电量分解算法的有效性，采用了由Pecan Street Dataport提供的美国德克萨斯州奥斯汀市以及纽约州伊萨卡岛的开源数据进行仿真 [11]。经过数据预处理后，奥斯汀市数据集包含了共24个居民用户，计量时间为2018年1月1日至2018年12月31日。伊萨卡岛数据集包含了共18个居民用户，计量时间为2019年1月5日至2019年10月31日。两组数据的采样频率均为每15分钟1个点。本文设日间时段为06:30至17:30。

分解结果采用均方根误差(Root Mean Square Error, RMSE)和变化系数(Coefficient of Variation, CV)作为精度评价指标。RMSE和CV的计算式如下：

$\text{RMSE}=\sqrt{\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left({\hat{P}}_{i,t}-P_{i,t}\right)}^2}}$ (16)

$\text{CV}=\frac{1}{N}{\displaystyle \underset{d=1}{\overset{N}{\sum }}\frac{\sqrt{{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left({\hat{P}}_{i,d,t}-P_{i,d,t}\right)}^2}}}{{\displaystyle \underset{t=1}{\overset{T}{\sum }}{P}_{i,d,t}}}}$ (17)

式中， ${\hat{P}}_{i,d,t}$ 和 $P_{i,d,t}$ 为添加了日期索引的 $P_{i,t}$，d表示日期索引。

3.2. 社区内用户的光伏发电量相关性分析

所提光伏发电量算法可实现的关键点在于社区内不同的光伏设备的PV发电量曲线的形态是近似的。为验证假设的合理性，使用皮尔逊相关系数(Pearson Correlation Coefficient, PPC)来评估不同用户间光伏发电量曲线的线性相关性 [12]。图1和图2以合理图的方式，展示了奥斯汀市用户和伊萨卡岛用户的PPC。图中横轴和纵轴表示为用户编号。PPC的取值范围为−1到1，PPC取值越接近于1，说明两变量间的正相关性越强。

从图1和图2中可以看出，社区用户之间的光伏电量都具有非常强的线性相关性，PPC数值基本大于0.9。图1和图2中呈白色的区间表示该用户并未安装光伏设备，因此其PV装机容量 $\alpha$ 为0。根据图中所呈现的相关性可知，社区内不同的光伏设备的PV发电量曲线的形态是近似的这一假设是合理的。

Pecan Street Dataport提供的用户数据集中，并未保证用户是处于同一社区内的。这将在一定程度上影响用户间的PV发电量曲线的相关性。若采集的用户数据在地理位置上比较集中，如在同一馈线下，相关系数会更高，这将更适用本算法所提PV发电量分解场景。

Figure 1. Pearson correlation coefficient matrix for customer PV generation in Austin

图1. 奥斯汀市用户光伏发电量皮尔逊相关系数矩阵

Figure 2. Pearson correlation coefficient matrix for customer PV generation in Ithaca

图2. 伊萨卡岛用户光伏发电量皮尔逊相关系数矩阵

3.3. 所提PV分解算法性能分析

在本节中，所提PV分解算法将与文献 [6] 和 [11] 中提出的分解算法进行分解精度对比。需要说明的是，文献 [6] 基于光伏物理模型假设的分解算法(为简便，下称为方法1)和文献 [13] 基于数据驱动的分解算法(为简便，下称为方法2)在建模时都需要用到太阳辐照度和温度等外生变量。相较之下，所提分解算法在建模时只需要社区中相同类型用户的净负荷数据，极大地降低了数据的依赖性与获取成本，有较好的实际应用价值。方法1和方法2建模所用到的气象数据来自于美国太阳辐射数据库(National Solar Radiation Database, NSRDB) [14]。

为说明所提算法的PV发电量分解有效性，以奥斯汀数据集以及伊萨卡岛数据集中的2号用户为例，进行分解结果的分析。表1和表2展示了2号用户不同PV发电量分解算法下，全年的日平均RMSE和CV。

Table 1. Daily RMSE and CV of various disaggregation methods of user #2 in Austin, Texas of a whole year

表1. 奥斯汀市2号用户在不同PV发电量分解算法下全年的日平均RMSE和CV

Table 2. Daily RMSE and CV of various disaggregation methods of user #2 in Ithaca, New York of a whole year

表2. 伊萨卡岛2号用户在不同PV发电量分解算法下全年的日平均RMSE和CV

从表1和表2可以看出，三种算法具有相近的分解精度，所提分解算法在奥斯汀市的数据集上取得了最好的RMSE分解结果，但总体来说三种方法的分解误差差异很小。但是，所提算法可以在不依赖外生的太阳辐照度和温度数据的情况下获得与其他两种方法相近的结果，这在实际应有中具有巨大的优势。分析表3可知，在伊萨卡岛数据集中，所提算法分解结果略差于其他两种方法。其中的原因可能是纽约数据集的居民用户比奥斯汀数据集少，因此难以搜寻到具有类似负荷消耗行为的用户，但所提算法在如此低的用户数据量以及外生数据的需求下，CV仅为9.556%是可以接受的。图3和图4展示了2号用户在不同PV发电量分解算法下一周的PV发电量分解结果。

Figure 3. Disaggregation results for one week for customer #2 in Austin of various PV generation disaggregation methods

图3. 多种PV光伏发电量分解方法下奥斯汀市2号用户一周的分解结果

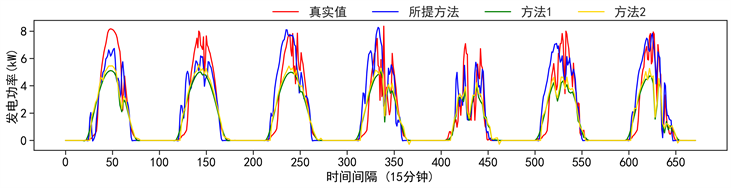
Figure 4. Disaggregation results for one week for customer #2 in Ithaca of various PV generation disaggregation methods

图4. 多种PV光伏发电量分解方法下伊萨卡岛2号用户一周的分解结果

由图3和图4可以看出，所展示的光伏发电量分解结果是针对单个用户的小型分布式发电设备的，因此真实的光伏发电曲线会出现较多的毛刺和波动。方法1和方法2的PV发电量分解曲线相较来说会更加光滑，这是因为两种方法均采用了外生的辐照度数据作为数据进行光伏发电量的分解的。外生辐照度数据是由NSRDB于临近气象站通过辐照度监测仪采集所得，一般架设在较为宽阔的地带，因此较少出现阴影遮挡的状况。但正是由于外生数据采集地点与待分解用户的PV发电地点不一致，导致外生气象数据无法真实的反映待分解用户所在地点的气象状况，引入了额外的误差。所提算法由于不依赖于外生气象数据，因此可更加真实的反映待分解用户的实际光伏发电量情况，分解结果也会与真实值一致，具有更多的毛刺，更能反映光伏发电量因如云层运动造成的阴影遮蔽等因素所导致的能量波动情况。

3.4. PV发电量分解消融实验

数据集中的居民用户数量是所提算法的一个重要参数。从理论上来说，社区用户的规模越大，越有可能匹配具有相似用电行为的用户，最终的PV发电量分解精度将会更高。为说明上述推断的合理性，本节进行了PV发电量的消融实验，分析在不同社区用户规模下的分解结果变化。

本实验采用奥斯汀市的用户数据集，实验对象仍然为2号用户，通过有放回的随机抽样方式，选取该数据集中的其他用户，形成用户数量分别为8、16、24的3个新数据集。表3展示了所包含用户数量不同的数据集下，2号用户的分解结果。

Table 3. Disaggregation results for user #2 under different data sets with different number of users

表3. 用户数量不同的数据集下2号用户的分解结果

分析表3可知，当数据集中用户数量下降，PV发电量的RMSE和CV随之增加，即PV发电量的分解精度下降。当数据集中用户量为原数据的三分之一时，PV发电量的RMSE由0.540 kW上升至了0.766 kW，CV由8.235%上升至了12.334%。造成精度下降的原因可解释为，随着数据集中用户数量的下降，可匹配的最优的具有相似用电行为的用户，可能为包含有所有用户的原数据集中的次优匹配结果。因此，所提算法若想获得更高的分解精度，可考虑使用包含有尽可能多的用户的数据集，并尽可能保证所有用户处于同一社区内或同一馈线下。

4. 结论

本文提出一种BTM系统下的PV发电量分解技术，该技术最大的优势在于能够在不依赖于任何外生气象数据，仅使用社区内其余用户的净负荷数据的情况下，实现用户的PV发电量分解。因为较低的外生数据依赖性，所提PV发电量分解算法具有较好的实际应用价值。通过使用美国德克萨斯州奥斯汀市以及纽约州伊萨卡岛的开源数据进行仿真，结果发现，与已有的依赖于外生气象数据的基于物理模型假设的和基于数据驱动的分解算法相比，本文所提PV发电量分解算法在更少的数据量需求下，仍获得了较高的分解性能，与其余两种分解算法的求解结果接近。同时，如果打算使用本文所提算法获得更高的分解精度，应考虑使用包含有尽可能多用户的数据集，并尽可能保证所有用户处于同一社区内或同一馈线下。