径流–渗流条件下边坡监测预警方法研究

Research on Slope Monitoring and Early Warning Method under Runoff-Seepage Conditions

摘要: 为进行降雨条件下的边坡稳定性影响研究，本文建立了滑坡的径流–渗流模型。在该模型中坡面径流采用Navier-Stokes方程描述，渗流采用Brinkman-extended Darcy方程描述。同时水体的流动又满足质量守恒方程。根据以上方程可以推导出径流和渗流中的流速分布特征。之后引入Newton内摩擦定律可以求出水流对边坡产生的拖曳力。利用该力重新修正了预应力锚索测量下滑力的公式，根据现场测量出的下滑力大小可以判断出边坡处于不稳定和裂缝发展阶段。结果表明：该公式有更好的适用性。

Abstract: In order to study the influence of slope stability under rainfall conditions, a runoff-seepage model of landslides is established in this paper. In this model, the slope runoff is described by the Navier-Stokes equation, and the seepage is described by the Brinkman-extended Darcy equation. At the same time, the flow of the water body satisfies the mass conservation equation. According to the above equations, the flow velocity distribution characteristics in runoff and seepage can be deduced. Then Newton’s law of internal friction can be introduced to calculate the drag force generated by the water flow on the slope. Using this force, the formula for measuring the sliding force of the prestressed anchor cable is re-corrected. According to the sliding force measured on site, it can be judged that the slope is in the stage of instability and crack development. The results show that the formula has better applicability.

1. 引言

降雨诱发滑坡的研究是边坡工程中一直难以解决的问题之一。国内外有相当多专家学者对降雨诱发滑坡进行了卓有成效的研究。岑越和刘振平等人为找出降雨天数与裂缝位移之间的联系，利用有效降雨量模型与皮尔逊相关系数的计算方法提出滑坡位移发展与有效降雨量呈现出显著相关 [1]。彭思佳等人采用雷达干涉测量方法(SBAS-InSAR)对窑街矿区进行形变监测 [2]。

但是以上的研究仅仅是滑坡发生的必要条件并不是滑坡发生的充要条件。因此不能准确地对滑坡的发生有充分的认识。

2. 工程概况

采石场位于北京市延庆区黄峪口村西侧，出露地层为蓟县系。采石场采取白云岩后经遗留所形成了如下图所示的边坡。在采石过程中对地形地貌有严重的破坏，形成了有临空面的山体条件，为滑坡的形成提供了卸载条件。目前，该边坡体前缘标高为+620 m，后缘标高为+780 m，地形起伏较大，边坡上缓下陡，自然坡度为20˚~45˚，见图1所示。

Figure 1. Landslide overview

图1. 滑坡概况

依据钻探、探槽及地质测绘揭露，边坡主要分为三层，岩性如下表1所示。

Table 1. Stratigraphic lithology

表1. 地层岩性

降雨是导致边坡失稳的主要原因之一，该采石场位于温带大陆性季风气候区，温带与中温带半干旱与半湿润的过渡地带。根据气象局资料2013~2017年年平均降水量为449.76 mm，且年内降水量变化大，降水主要集中在夏秋两季(6~10月)，占年总降水量的90.6%以上，平均月降雨量统计如下图2所示。

Figure 2. Average monthly rainfall

图2. 平均月降雨量

6~10月也为滑坡发生较多的月份，滑坡数占全年的90%以上，滑坡的发生时间与强降雨时间的分布非常契合。如2017年6月21日延庆区发布蓝色暴雨预警，每小时降雨量可达50 mm以上，同时边坡上发生了大规模的滑坡且对边坡下部支挡结构造成了严重的破坏，其具体情况如下图3所示。综上所述，降雨与滑坡灾害发生之间有紧密的关系，因此对降雨与滑坡的关系研究意义重大。

图3. 降雨诱发滑坡造成的破坏

3. 流场分析及切应力计算

3.1. 应用模型

在自然降雨条件下，坡体上的水流的运动形式一般为三维，且有众多影响因素，不方便进行研究。因此，本文提出了以下基本假设将模型进行简化：

1) 边坡和径流可沿x方向无限延伸；

2) 边坡坡体介质均匀；

3) 水流为层流且仅在平面内运动；

4) 水体不可压缩，即满足连续性方程；

5) 径流流动可用Navier-Stokes方程进行描述；

6) 渗流可用Brinkman-extended Darcy方程进行描述 [3]。

如下图4所示为建立的径流–渗流模型。在该模型中边坡坡度为β，长度为L，厚度为b，孔隙率为n，渗透率为K，边坡内沿x方向的流速为v_x，坡面径流水深为h，沿x方向的流速为u_x。

Figure 4. Runoff analysis model

图4. 径流分析模型

3.2. 径流的满足的方程

径流中的水体流动满足质量守恒方程和Navier-Stokes方程，质量守恒方程即也叫做连续性方程，N-S方程即水体满足的动量方程。

质量守恒方程为：

$\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}=0$

式中 $u_x$ 、 $u_y$ 、 $u_z$ 分别表示地表径流中沿x、y、z方向的流速。

由于基本假设了坡面径流沿y方向和z方向的流速为0，所以质量守恒方程中后两项为0 ( $\frac{\partial u_y}{\partial y}=0$, $\frac{\partial u_z}{\partial z}=0$ )，因此可得 $\frac{\partial u_x}{\partial x}=0$，上式表示 $u_x$ 在x方向上大小不变。

沿x方向的N-S方程为：

$f_x-\frac{1}{\rho }\frac{\partial P}{\partial x}+v\left(\frac{{\partial }^2{u}_x}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial y^2}+\frac{{\partial }^2{u}_x}{\partial z^2}\right)=\frac{\partial u_x}{\partial t}+u_x\frac{\partial u_x}{\partial x}+u_y\frac{\partial u_x}{\partial y}+u_z\frac{\partial u_x}{\partial z}$

式中 $f_x$ 为x方向的质量力， $\rho$ 为水的密度，P为压强沿x方向的分量，v为水的运动粘滞系数。

由于 $u_x$ 在z方向不会发生变化，所以有 $\frac{\partial u_x}{\partial z}=0$，同时沿x方向上的质量力 $f_x=g\sin \beta$， $\text{d}P/\text{d}x=-\Delta P/L$，径流流速不随时间变化，即 $\frac{\partial u_x}{\partial t}=0$。将以上条件代入N-S方程化简可得：

$\eta \frac{{\partial }^2{u}_x}{\partial y^2}+\frac{\Delta P}{L}+{\gamma }_w\sin \beta =0$

式中 $\eta$ 为水的动力粘滞系数， ${\gamma }_w$ 为水的容重。

上式为二阶常系数齐次线性微分方程，求解该方程可得：

$u_x=-\frac{\Delta P+{\gamma }_{w}L\sin \beta }{2\eta L}{y}^2+A_{1}y+A_2$

式中A₁，A₂为未知系数。

3.3. 边坡渗流的流速分布

在边坡坡体内的渗流满足质量守恒方程和Brinkman-extended Darcy方程。

连续性方程可以写成：

$\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}=0$

式中 $v_x$ 、 $v_y$ 、 $v_z$ 分别表示渗流沿x、y、z方向的流速。

沿x方向的Brinkman-extended Darcy方程为：

$n\rho f_x-n\frac{\eta }{K}{v}_x-n\frac{\partial P}{\partial x}+\eta \left(\frac{{\partial }^2{v}_x}{\partial x^2}+\frac{{\partial }^2{v}_x}{\partial y^2}+\frac{{\partial }^2{v}_x}{\partial z^2}\right)=\frac{\rho }{n}\left(v_x\frac{\partial v_x}{\partial x}+v_y\frac{\partial v_x}{\partial y}+v_z\frac{\partial v_x}{\partial z}\right)$

因为 $\frac{\partial v_x}{\partial x}=0$， $\frac{\partial v_x}{\partial z}=0$， $v_y=0$， $v_z=0$ 化简上式可得：

$\frac{{\text{d}}^2{v}_x}{\text{d}{y}^2}-n\frac{v_x}{K}+n\frac{\Delta P}{\eta L}+n\frac{{\gamma }_w\sin \beta }{\eta }=0$

上式同样为二阶常系数齐次线性微分方程，求解该方程可得：

$v_x=C_1{\text{e}}^{y\sqrt{n/K}}+C_2{\text{e}}^{-y\sqrt{n/K}}+\frac{\left(\Delta P+{\gamma }_{w}L\sin \beta \right)K}{\eta L}$

式中C₁、C₂为未知系数。

3.4. 边界条件

径流的流速满足以下边界条件 [4]：

1) 在径流表面上，径流流速达到最大值，即当 $y=b+h$ 时，有 $\text{d}{u}_x/\text{d}y=0$ ；

2) 在坡面处满足流速大小相等，即当 $y=b$ 时，有 $u_x=v_x$ ；

3) 在坡面处剪应力连续，即当 $y=b$ 时，有 $\frac{1}{n}\frac{\text{d}{v}_x}{\text{d}y}=\frac{\text{d}{u}_x}{\text{d}y}$ ；

4) 在边坡底部渗流流速等于0，即当 $y=0$ 时， $v_x=0$。

为方便计算，需对 $u_x,v_x$ 的表达式进行简化。令式中， $-\frac{\Delta P+{\gamma }_{w}L\sin \beta }{2\eta L}=E$， $\sqrt{n/k}=F$。则表达式简化为：1) $u_x=E{y}^2+A_{1}y+A_2$，2) $v_x=C_1{\text{e}}^{yF}+C_2{\text{e}}^{-yF}-2KF$。

根据边界条件1可以解出 $A_1=-2E\left(b+h\right)$，。将边界条件2、3、4代入 $u_x,v_x$ 的表达式，可以列出方程 $C_{1}F{\text{e}}^{bF}-C_{2}F{\text{e}}^{-bF}=-2nEh$， $-E{b}^2-2Ehb+A_2=C_1{\text{e}}^{bF}+C_2{\text{e}}^{-bF}-2KF$， $C_1+C_2-2KF=0$ 联立上述三个方程可以解出 $C_1=\frac{-2nEh+2KF-{\text{e}}^{-bF}}{F\left({\text{e}}^{bF}+{\text{e}}^{bF}\right)}$， $C_2=2KF-\frac{-2nEh+2KF-{\text{e}}^{-bF}}{F\left({\text{e}}^{bF}+{\text{e}}^{bF}\right)}$， $A_2=C_1{\text{e}}^{bF}+C_2{\text{e}}^{-bF}-2KF+E{b}^2+2Ehb$。

3.5. 切应力分析

根据Newton内摩擦定律可知：

$\tau =\eta \frac{\text{d}u}{\text{d}y}$

将坡面径流流速代入上式，求出在坡面上沿x方向的切应力为：

$\begin{array}{l}{\tau }_{x1}=\eta \left(2Ey+A_1\right)=-2E\eta \left(y-b-h\right)\\ =-\frac{\Delta P+{\gamma }_{w}L\sin \beta }{L}\left(y-b-h\right)\end{array}$

由于 $\Delta P={\gamma }_w\Delta H$， $\Delta H=iL$， $i=\tan \beta$，所以 ${\tau }_{x1}=-{\gamma }_w\left(y-b-h\right)\left(\tan \beta +\sin \beta \right)$。当 $y=b$ 时， ${\tau }_{s1}={\gamma }_{w}h\left(\tan \beta +\sin \beta \right)$。

4. 滑动力监测力学模型预警准则

4.1. 力学模型

在以往提出的滑坡力学模型中，没有考虑到降雨对滑坡发生的作用，因而在进行指标换算时具有一定的误差，在此重新进行公式推导，使滑动力监测公式在降雨条件下同样更加地适用。滑坡力学模型如下图5所示。

对边坡进行受力分析，岩土体所受到的作用力包括：竖直向下的重力，锚索带来的摄动力，沿滑面向下不可测的滑动力，平行于坡面向下的拖曳力，渗流力和沿坡面向上的摩擦力。

其中沿滑面向下的拖曳力为 $F_{d1}={\gamma }_{w}hL\left(\tan \beta +\sin \beta \right)\cos \left(\beta -\alpha \right)$，渗流力为 $F_{d2}={\gamma }_{w}Lb\tan \beta \cos \left(\beta -\alpha \right)$，摄动力为 $P_t=P\cos \left(\theta +\alpha \right)$， $F_{\phi }=\left(P_n+G_n\right)\tan \bar{\phi }+cl$

由受力分析图可沿滑动面列平衡方程为， $P_t+F_{\phi }=G_t+F_{d1}+F_{d2}$，则可求下滑力为

$\begin{array}{c}{G}_t=P\left[\cos \left(\theta +\alpha \right)+\sin \left(\theta +\alpha \right)\tan \bar{\phi }\right]+G\sin \left(\theta +\alpha \right)\tan \bar{\phi }\\ -{\gamma }_{w}Lb\cos \left(\delta -\alpha \right)\tan \delta -{\gamma }_{w}h\left(\tan \delta +\sin \delta \right)\cos \left(\delta -\alpha \right)\end{array}$

其中， $\alpha$ 为滑面倾角， $\bar{\phi },c$ 分别为岩土体的加权内摩擦角平均值和加权凝聚力平均值，G为滑体的重力， $G_t$ 为沿滑面向下不可测的滑动力，P为锚索上施加的预应力。

基于上述理论可得，不可测量的下滑力可以表示为预应力P的函数，同时在降雨条件下又根据拖曳力和渗流力使该方程在此不利条件下更加地准确有效，提高了监测预警的能力。

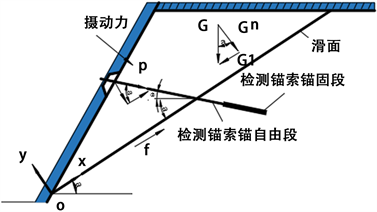
Figure 5. Landslide mechanics monitoring model

图5. 滑坡力学监测模型

4.2. 监测数据分析

如图6和图7所示，一号和二号监测点下滑力在2021年8月3日前始终保持在300 KN左右，之后

Figure 6. No. 1 monitoring point data

图6. 1号监测点数据

Figure 7. No. 2 monitoring point data

图7. 2号监测点数据

逐渐增长到400 KN。

同时基于其他丰富的现场监测经验，总结出4种滑坡监测预警模式，即稳定模式、不稳定模式、裂缝破坏模式和滑移模式。在稳定模式下，下滑力随着时间的增长基本保持不变，曲线处于平稳状态；在不稳定模式下，随着时间的增长下滑力缓慢上涨，曲线呈上升的状态；在裂缝破坏模式下，下滑力曲线会发生跳跃，大的跳跃代表有大裂缝，小的跳跃代表有小裂缝；在滑移模式下，监测曲线会多次有突降的征兆，表明边坡内部的裂缝已经贯通形成滑动面，此时边坡已经处于不稳定状态 [5] [6] [7] [8]。

因此可以判断，1号监测点处曲线满足不稳定模式曲线、2号监测点处曲线基本满足裂缝发展模式曲线，且为小裂缝。

5. 结论

本文利用Navier-Stokes方程、Brinkman-extended Darcy方程和连续性方程推导出了降雨条件下的径流流速场和渗流流速场分布规律公式。并利用该结果计算出了坡体表面所受到的水流拖曳力大小。由公式可知，该力与水流深度和边坡坡度的大小成正比。因此降雨强度越大，水流的效应就越明显。

之后由此修正了监测预警中的下滑力计算公式。通过现场数据结果可知，修正后数据更加精确可靠，因此可以判断出黄峪口边坡目前处于不稳定和裂缝发展阶段。