基于S型组合曲线的隧道洞口段施工地表沉降预测分析

Analysis of Surface Settlement Prediction of Tunnel Portal Section Construction Based on the S-Shaped Composite Curves

摘要: 隧道洞口段施工易引起上覆地表大面积沉降，对洞口边坡稳定产生较大威胁。施工引起的地表累积沉降通常呈现为S型变化规律，选取5种S型曲线(Logistic、Gompertz、Richards、Weibull及MMF曲线)分别运用于黄泥岗头隧道洞口段施工诱发地表沉降预测，分析各单一模型的预测效果。利用加权平均算法获得5种曲线的组合权重值，构建组合S型曲线预测模型。结果表明：MMF模型在5种单一S型曲线中拟合效果最好；通过权重优化得到组合模型，其拟合评价R2及RMSE值均优于单一模型，提高了地表沉降预测精度，验证了该方法的地表沉降预测有效性。

Abstract: The construction of tunnel portal section is easy to cause a large area of settlement on the overlying surface, which poses a great threat to the stability of tunnel entrance slope. The surface accumulated settlement caused by construction usually shows an S-shaped variation law. This paper selects five commonly used S-shape curves (Logistic, Gompertz, Richards, Weibull and MMF curves) and respectively applies them to the prediction of ground surface settlement caused by Huangnigangtao tunnel, and the prediction effects of each single model are analyzed. The weighted average algorithm is used to obtain the combined weight values of five curves and the S-shaped composite curve is built. Results show that MMF has the best fitting effect among five single S-shaped curves. The combined model was obtained by weight optimization, and its fitting evaluation R2 and RMSE values were better than that of the single models, which improved the prediction accuracy of surface subsidence and verified the validity of the proposed method.

1. 引言

隧道洞口段施工开挖势必引起周围岩土体沉降、变形，导致地表塌陷。为了有效降低隧道开挖过程中地表沉降带来的危害，必须深入研究地表沉降相关特征及其发展过程，预测地表沉降变形值。

近年来，专家学者采用多种预测方法分析地下结构开挖沉降变形。宋卫东等 [1] 运用FLAC软件分析了浅埋暗挖车站主体在不同施工及支护方式下，周边土体应力及地表位移变化情况。董俊 [2] 分析了顶管施工引起地表沉降演化和建筑物基础不均匀沉降规律。张文龙 [3] 研究了浅埋暗挖通道施工地表沉降规律，表明超前小导管注浆能够有效减小地表沉降量，是有效地浅埋暗挖通道辅助施工措施。李荣伟等 [4] 对比了超前加固下手掘顶管、土压顶管施工对地表沉降控制效果，发现地下水位以上的砂土层，土压式顶管施工效果较好。吴锋波等 [5] 研究了盾构区间隧道的地表变形特征，得到了地层损失率和宽度参数与隧道埋深的相关性。Chen等 [6] 分别采用回归分析及时间序列方法预测大断面隧道围岩变形，结果显现时间序列方法在短期内预测精度较高，回归分析方法精度依赖于参数选择的正确性。上述研究方法由于计算量大、计算模型选取单一等问题，造成计算结果与实际开挖沉降量存在一定偏差。

Logistic、Gompertz、Richards、Weibull及MMF等5种S型曲线均能在一定程度上反映地表沉降发展规律，但是由于自身拟合特征的局限，难以适应不同工况条件的地表沉降预测。在考虑各曲线特征和局限性的基础上，运用加权平均算法，获得各种S型曲线的组合权重值，构建组合预测模型，并将其运用于浙江文成县黄泥岗头隧道洞口施工诱发地表沉降预测，验证组合预测模型的合理性。

2. 地表沉降规律

隧道洞口施工引起地表沉降是一个复杂的空间问题，受到多种因素影响。已有研究表明施工引起地表沉降会持续一段时间直至静止，并随时间增加，沉降曲线大致呈S型 [7] [8]，如图1所示。梅国雄等 [9] 根据土体本构从理论上证明了线性荷载作用下地表沉降曲线呈S型变化。

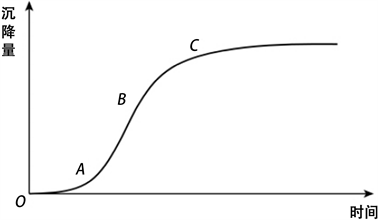
Figure 1. Laws of ground surface settlement

图1. 地表沉降规律

由图1可知，地表沉降的发展过程随着时间的推移可以分为四个阶段。

① 初始沉降阶段OA：沉降速度较慢，沉降量随时间增加缓慢。

② 加速沉降阶段AB：沉降速度随时间增加而增大，并达到极限。也就是说，沉降呈快速增长趋势。

③ 稳定沉降阶段BC：随着时间的推移，沉降量继续增大，沉降速度逐渐减小。

④ 最终沉降阶段CD：沉降速度继续减小，最终趋于0。同时，沉降增长缓慢，接近极限。

3. 组合S型曲线预测模型

3.1. S型曲线

S型曲线又称增长曲线，被广泛运用于社会、经济预测，用于描述事情产生、发展、成熟最终达到极限状态的系统过程，比简单的时间序列技术更为准确 [10]。S型曲线有多种形式，其中Logistic、Gompertz、Richards、Weibull及MMF曲线是较为常用的5种类型，均能较好地反映地表沉降发展过程。各曲线模型公式如下所示：

① Logistic曲线：

$y_1\left(t\right)=\frac{a}{1+b{e}^{-ct}}$ (1)

② Gompertz曲线：

$y_2\left(t\right)=a{e}^{-b{e}^{-ct}}$ (2)

③ Richards曲线：

$y_3\left(t\right)=\frac{a}{1+e^{{\left(b-ct\right)}^{1/r}}}$ (3)

④ Weibull曲线：

$y_4\left(t\right)=a-b{e}^{-c{t}^r}$ (4)

⑤ MMF曲线：

$y_5\left(t\right)=\frac{bc+a{t}^r}{c+t^r}$ (5)

式中，y为累积沉降量；t为时间；a为最终沉降量；b为与曲线截距有关参数；c为瞬时沉降速率；r为拟合参数，用于增加数据拟合的灵活性。

由式(1)~式(5)可知，各类S型曲线均单调递增，存在拐点。当t趋于无限大时，存在极大值a，可以较准确地反映地表沉降的变化规律。

3.2. 组合S型曲线

由于不同S型曲线所描述的变化趋势存在差异，所反映的地表沉降规律也不相同，采用多种曲线分别对实际监测数据进行拟合，可以充分利用各曲线特征，选出拟合精度最高的预测模型 [11]。但是该方法仍然只能利用一条曲线特征，拟合效果还显得不足。因此，本文引入组合预测的思想，将S型曲线组合起来，根据实测数据变化特征，对各曲线配以适当的权重，能够将各曲线适合该工况的特征充分发挥，减小其不利特征的影响，获得比单一预测模型更好的拟合效果。利用加权平均的组合模型计算过程如下：

设原始监测数据为x_t， $t=1,2,\cdots ,n$，利用m种曲线对其进行拟合预测， $x_t^i$ 为第i种方法t时刻的预测值， $i=1,2,\cdots ,m$。设ω_i为第i种曲线的组合预测中的权重，并满足归一性及非负性，计算过程如下。

${\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i=1}\left({\omega }_i\ge 0\right)$ (6)

则加权算术平均组合预测值可表示为：

${x^{\prime }}_t={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i{x}_{it}}$ (7)

设 $e_t^i=x_t-x_t^i$ 为t时刻第i种预测方法的误差，则该时刻组合模型的误差为：

$e_t=x_t-{x^{\prime }}_t={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i\left(x_t-x_{it}\right)}={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i{e}_{it}}$ (8)

组合预测总误差平方和为：

$E={\displaystyle \underset{t=1}{\overset{N}{\sum }}{e}_t^2}={\displaystyle \underset{t=1}{\overset{N}{\sum }}{\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i{e}_{it}}\right)}^2}$ (9)

因此，基于最小二乘法，为获得最佳权重w_i，应使误差平方和达到最小，即满足下式：

$\{\begin{array}{c}\min E\\ {\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i=1}\\ {\omega }_i\ge 0\end{array}$ (10)

4. 工程应用

4.1. 工程概况

黄泥岗头隧道是浙江文成县的进出通道，全长3920 m。隧道洞口浅埋、围岩条件差，地表沉降控制难度大。为了解施工过程中地表沉降变化，沿隧道轴线方向间隔10 m布置一组地表监测点，掌子面正上方的实测典型地表累积沉降量如图2所示。

4.2. 单一曲线预测

以上述隧道洞口段实测地表沉降数据为研究对象，采用5种S型曲线分别进行拟合，参数计算结果及确定系数R²如表1所示，实测曲线与不同预测曲线间的对比如图3所示。

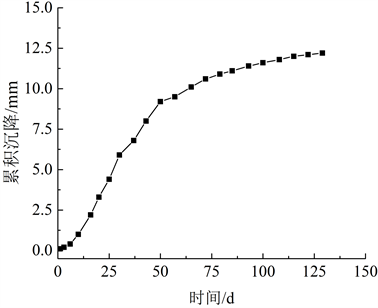
Figure 2. Measured cumulative surface settlement

图2. 实测地表累积沉降

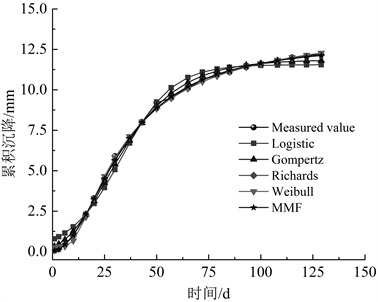
Figure 3. Comparison of predicted and measured curves

图3. 预测及实测曲线对比

Table 1. Fitting parameters of S-shaped curves

表1. S型曲线拟合参数

根据表1中各S型曲线拟合结果的确定系数R²可知，对实测地表累积沉降量采用单一模型拟合均有较好精度；对比5种曲线，MMF模型的确定系数最大(R² = 0.9754)，说明拟合度最好。从图3中也可以发现，地表沉降明显经历了初始沉降–加速沉降–稳定沉降–极限沉降的四个阶段，各拟合曲线与实际监测曲线的趋势是一致的，但是预测数据与实测数据存在一定的偏差。在地表沉降的不同阶段，各模型的误差也有所不同。在初始沉降与稳定沉降阶段，各模型的误差较大；而加速沉降阶段的误差相对较小。

4.3. 组合预测分析

采用上述组合预测方法，利用Matlab编制计算程序，获得各种S型曲线的组合权重值。由于Gompertz曲线的权重为负，剔除该模型后重新进行组合，得到各曲线权重值如表2所示。组合预测模型预测值与实测值对比如图4所示。

Table 2. Combination weights of S-shaped curves

表2. S型曲线的组合权重

Figure 4. Comparison of predicted and measured settlement

图4. 预测及实测沉降量对比

4.4. 对比分析

如表1所示，地表某时刻总沉降量可以通过不同模型对应公式进行求解，从而获得不同模型与实测数据的对比图(图3)。为了对比分析组合模型与单一模型的沉降预测效果，可计算获得不同模型RMSE值，如下式所示：

$RMSE=\sqrt{\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(y-y^{\prime }\right)}^2}}$ (11)

式中，y、y'分别为实测沉降值与预测沉降值；N为数据总数。RMSE值越小，预测效果越好。各模型R²及RMSE值如表3所示。

如表3所示，MMF模型的R²及RMSE值分别为0.9754、0.1047，说明MMF模型在5种单一S型曲线中拟合效果最好。而采用权重组合(Logistic 1.03%, Richards 17.26%, Weibull 23.90%, MMF 55.78%)所形成的组合模型确定系数R² = 0.9993，比单一模型的确定性系数最大值(R² = 0.9754)增大了2.45%，RMSE = 0.0832，比单一模型最小值(RMSE = 0.1047)降低了25.84%，说明组合模型的拟合效果优于MMF模型，

Table 3. Values of R2 and RMSE for each model

表3. 各模型R²及RMSE值

验证了该组合模型在隧道洞口段施工地表沉降预测方面的有效性。

5. 结论

1) 根据地表沉降的发展规律和对现场监测数据的分析，地表沉降的发展过程可分为初始沉降阶段、加速沉降阶段、稳定沉降阶段和最终沉降阶段四个阶段。隧道洞口施工导致地表沉降规律与S型曲线的变化规律一致。

2) 将5种S型曲线应用于浙江文成县黄泥岗头隧道洞口诱发地表沉降预测，均取得了较好的效果。在单一预测模型中，MMF模型预测精度最高，说明其曲线特性更加适合于隧道洞口段施工地表沉降规律。

3) 基于加权平均算法的组合预测模型弥补了单一预测模型对地表沉降预测的不足，充分发挥各曲线适合不同工况的特征，减小不利特征对沉降预测的影响，有效地提高了隧道洞口段施工地表沉降预测精度。

基金项目

浙江省建设科技项目(2021K123)，浙江省交通科技项目(2020004)。