1. 引言
海洋工程用钢长期在恶劣环境下服役,考虑到海浪、风暴、寒流等气候环境的影响,对钢材的强韧性、低温冲击韧性、耐蚀性等性能提出了苛刻要求 [1]。本文研究的是海洋平台用EH460钢,原始锻坯厚度为300 mm,现欲将其加工至厚度为100 mm,在厚板加工过程中,控制组织和性能在厚度方向的均匀性是一大难题,表面和心部性能差异大容易在服役期间失效,现在也有很多关于提升厚板性能方面的研究,李海军 [2] 等通过控制轧制温度、压下量等使变形从表面向心部渗透,减小了厚度方向的差异性,提高组织的均匀性。刘朋 [3] 通过研究3500 mm中厚板生产线的出钢温度、轧机负荷和轧制节奏等提高了钢材的成材率、细化了晶粒,改善了钢材性能。针对前人已有研究可知,合理设置加工工艺参数可以优化组织和性能,然而不同钢种的热加工参数也不尽相同,如何选取合适的参数以达优化组织性能的目的还需通过研究钢材的热变形行为。通过热压缩试验可知:真应力–真应变曲线可反映流变应力与变形条件之间的关系,本构方程则可预测不同变形条件下的流变应力,热加工图可判断失稳区、安全区及变形机制,以上均可为材料在实际热加工过程中优选变形参数和组织调控提供依据 [4]。例如,孔晓寒 [5] 等通过研究热变形行为解释了铸态Q345E钢的变形机制,即动态回复主要发生在低温、大变形速率条件下,动态再结晶主要在高温、大变形速率条件下。王顺 [6] 等通过将2205/Q345叠加进行复合热压缩和采用SEM分析复合热压缩后的微观组织,探索出2205/Q345在变形速率为1~10 s−1、温度为1050℃~1100℃时热压缩复合效果最好。故在热加工前探索热变形行为是有必要的,且能为现场生产提供理论依据并具有指导意义。
本文基于海洋平台用EH460钢进行热压缩试验研究其热变形行为,通过分析真应力–真应变曲线、构建本构方程和绘制热加工图以探索EH460钢的最佳热加工工艺参数,为钢厂实际生产提供理论依据。
2. 材料与方法
试验材料取自某钢厂的EH460钢,其化学成分如表1所示,原始组织如图1所示。在Gleeble-1500热模拟试验机上进行单向轴对称热压缩试验,试样的尺寸为Φ10 mm × 15 mm。试验过程为:以5℃/s将试样加热到1100℃,保温2 min使其由表面至心部温度一致,再以10℃/s冷至预定变形温度,保温20 s再次使试样由表面至心部温度一致,对试样进行热压缩试验,变形温度为900℃~1150℃,变形速率分别为0.01、0.1、1和10 s−1,工程应变量为60%,最后以20℃/s的冷速快冷至室温。金相试样经磨抛后,采用4%硝酸酒精溶液进行侵蚀,然后利用CMY-310金相显微镜对显微组织进行观察。

Table 1. Chemical composition of EH460 steel (mass fraction, %)
表1. EH460钢的化学成分(质量分数,%)

Figure 1. Original microstructure of EH460 steel
图1. EH460钢的原始组织
3. 结果与讨论
3.1. 真应力–真应变曲线
图2为EH460钢的真应力–真应变曲线图,由图可知,EH460钢的热变形行为主要受加工硬化、动态回复和动态再结晶控制。根据加工硬化速率和动态软化速率可将真应力–真应变曲线分为三个阶段:1) 加工硬化速率大于动态软化速率,此时加工硬化占主导地位,流变应力随应变量的增加持续增大;2) 加工硬化速率小于软化速率,此时动态软化占主导地位,流变应力随应变量的增大而减小;3) 加工硬化速率等于软化速率,即加工硬化引起的位错增殖与动态软化产生的位错相抵消和重排达动态平衡,此时流变应力达动态平衡并保持稳定状态 [7]。
从图2中曲线可知,在变形温度不变时,流变应力随着变形速率的增加而增加。变形速率增加,位错迅速增殖致位错密度增大,变形阻力也随之增大,故流变应力也增大;同时位错可作为动态再结晶的形核核心,在应变量相同时,增大变形速率会使孕育形核时间不足,这在一定程度上抑制了动态再结晶的发生,减弱了软化作用 [8],故流变应力增大。
在变形速率不变时,流变应力随着变形温度的增加而降低。变形温度升高,原子热运动加剧,原子间结合力降低,扩散速率加快,易发生刃型位错的攀移、螺型位错的交滑移以及随后在新滑移面上异号位错相遇而发生抵消等过程;同时温度升高也会为位错提供挣脱Cottrell气团钉扎作用的能量,位错运动阻力减小,更易发生位错重排和湮灭等 [7] [9],流变应力也随之减小。

Figure 2. True stress-true strain curves and predicted value of EH460 steel (a) 0.01 s−1; (b) 0.1 s−1; (c) 1 s−1; (d) 10 s−1
图2. EH460钢的真应力–真应变曲线和预测值(a) 0.01 s−1;(b) 0.1 s−1;(c) 1 s−1;(d) 10 s−1
3.2. 加工硬化率
加工硬化率θ = dσ/dε可用于判断在变形过程中加工硬化和动态软化二者之间的强弱 [10],以1000℃、0.1 s−1为例,将真应力–真应变曲线和加工硬化率作于同一图中,如图3所示。在变形刚开始时,加工硬化率达到最大值,说明在微应变阶段,还未发生动态回复和动态再结晶,只有加工硬化;随着应变量的增大,试样逐渐发生动态回复和动态再结晶,加工硬化率逐渐减小,直至减为零并稳定在零附近,此时加工硬化和动态软化作用达到动态平衡;但当变形量继续增加时,流变应力增加,加工硬化率也增大至大于零,此时发生了二次硬化,原因是变形量增加,位错密度增加,此时加工硬化重新超过动态软化,呈现二次硬化的现象 [10]。
3.3. 构建本构方程
基于上述试验数据,在考虑温度补偿、变形速率补偿和应变补偿时可用双曲线正弦Arrhenius模型和Z (Zenner-Hollomon)参数来描述流变应力和变形条件之间的关系 [10] [11],如式(1)所示:
(1)
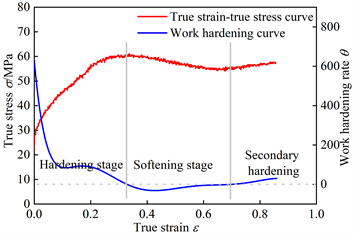
Figure 3. True stress-true strain and work hardening rate; 1000˚C, 0.01 s−1
图3. 真应力–真应变曲线和加工硬化率;1000℃,0.01 s−1
其中:
为变形速率,s−1;Q为变形激活能,kJ∙mol−1,是表征塑性变形能力的重要物理参数;n1、n、β和A为热变形系数,
;R为气体常数,8.314 J·(mol∙K)−1;T为热力学温度,K;σ为流变应力,MPa;Z参数为温度补偿的变形速率因子,即描述变形温度和变形速率之间的关系。
对式(1)两边取自然对数可得式(2);
(2)
由试验数据且结合式(2)分别作图,并对其进行线性拟合,可分别得
、
、
、
、
的线性拟合图,以
为例,作图如图4所示。

Figure 4. Linear fitting diagram of thermal deformation coefficient (a) n1; (b) β; (c) n; (d) Q; (e) lnA
图4. 热变形系数的线性拟合图(a) n1;(b) β;(c) n;(d) Q;(e) lnA
当ε = 0.3时,n1值取1150℃时线性拟合直线
的斜率,β值取900℃时线性拟合直线
的斜率;n、Q、A分别取
、
和
中所有线性拟合直线斜率的平均值。由各拟合直线的斜率最终可得α、n、Q、lnA分别为α = β/n1 = 0.0121 MPa−1、n = 5.435、Q = 324.284 kJ∙mol−1、lnA = 27.477 s−1。图4(e)中拟合直线的斜率即为n,其值为5.347,与图4(c)所得n的相对差为1.6%,在合理误差范围内。
假设热变形系数α、n、Q、lnA是关于应变ε的多项式函数,如式(3)所示,对这4个热变形系数进行多项式拟合,结果表明6次多项式拟合具有最好的相关性,如图5所示;拟合多项式系数如表2所示。
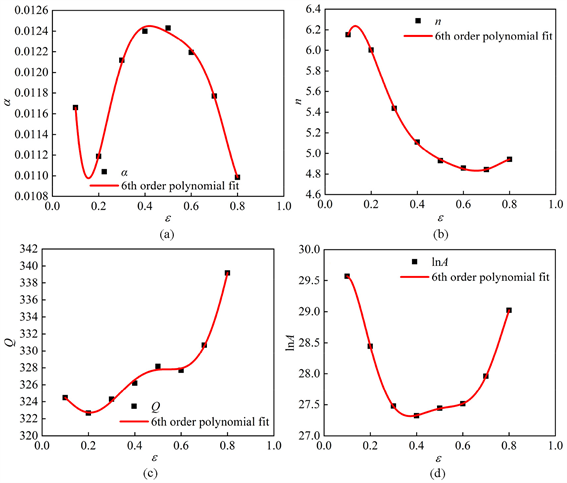
Figure 5. The relation curves between thermal deformation coefficient and strain (a) α; (b) n; (c) Q; (d) lnA
图5. 热变形系数和应变量的关系曲线图(a) α;(b) n;(c) Q;(d) lnA

Table 2. Thermal deformation coefficient under different strain conditions
表2. 不同应变量下的热变形系数
(3)
由上述关系可得EH460钢的流变应力方程,如式(4)所示。
(4)
为了检验式(4)预测流变应力的准确性,将应变量0.1~0.8 (0.05为间隔)分别代入式(3)和式(4)中求得在不同变形条件下的流变应力预测值,并将其与试验值进行对比,如图6所示,由图可知试验值和预测值的曲线走势大致相同,数据吻合较好。
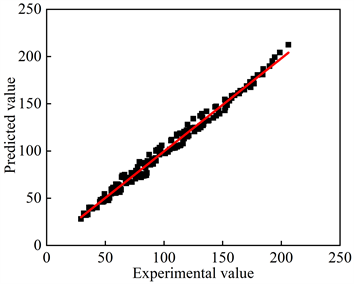
Figure 6. Correlation between experimental and predicted stresses
图6. 试验值和预测值的相关性
为了更全面的说明上述流变应力本构方程的预测精度,针对预测值和试验值将采用相关系数(R)和平均相对误差(AARE)来进行分析 [11],R和AARE表达式如(5)、(6)所示。
(5)
(6)
结合式(5)和(6)可得R值为0.994,AARE值为4.498%,相关性较好;故在本文试验参数条件下,流变应力本构方程具有较好的预测精度,可以较为准确的预测流变应力。
3.4. 热加工图
为了优选EH460钢的热加工参数以及避开热加工失稳区,基于动态材料模型(Dynamic Material Model, DMM)并根据上述试验数据可建立EH460钢的热加工图。其中DMM模型旨在阐述在热变形过程中外界对试验钢做功的转化方向,一部分是在热变形过程中以热量的形式耗散,即能量耗散量(G),另一部分在热变形过程中被组织转变消耗,即耗散协量(J) [12]。材料的热变形过程可用式(7)表示:
(7)
式中:σ为流变应力,MPa;K为常数;m为变形速率敏感指数,为表征塑性好坏的重要指标。
为了更准确的描述σ与
的关系,可用三次多项式表示如式(8)所示 [13] [14],结合式(7)、(8)可得m,如式(9)所示:
(8)
(9)
m还可表示为耗散协量和能量耗散量的比值,故m的范围为0~1,一般希望m接近1较好,说明材料的塑性好。要想准确判断材料的变形机制还需参考功率耗散因子η和失稳判据ξ。功率耗散因子η可反映微观组织转变的机理,一般认为η较大时更易发生动态回复和动态再结晶等,热加工性能更好 [13]。η可用变形速率敏感指数m表示为式(10):
(10)
失稳判据ξ是依据最大熵原理得出的,根据其值可用于判断材料的安全区和失稳区,如式(11)所示,ξ > 0表示安全区,理论上材料在该区域进行热加工的性能较好;ξ < 0表示失稳区,该区在热加工时可能发生绝热剪切带、局部流动等缺陷造成塑性失稳,在热加工时应尽量避开该区域。
(11)
由变形温度T、变形速率
和功率耗散因子η可绘制功率耗散图,利用功率耗散图可以判断变形条件和变形机制之间的联系;由变形温度T、变形速率
和失稳判据ξ可绘制失稳图,利用失稳图可以判断安全区和失稳区;将二者叠加可得在不同变形条件下的热加工图,如图7所示。通过对比应变量为0.2、0.4、0.6和0.8时的热加工图可知,热加工失稳区主要集中在900℃~1040℃,0.01~0.1 s−1、900℃~950℃,0.1~10 s−1、1080℃~1130℃,0.01~0.1 s−1和1070℃~1150℃,0.1~10 s−1区域内,应变量不同时,η峰值区域也有差异,且EH460钢在应变量为0.8时与实际生产过程中的热加工完成状态最为接近,故以0.8为参考分析EH460钢的最佳热加工区间 [11]。由图7(d)红框可知应变量为0.8时的峰值区域为1050℃~1100℃、0.1~10 s−1,理论上在此区域内相对其他区域更易发生动态回复和动态再结晶,可优选该区域作为热加工区域。同时结合不同应变量条件下的热加工图可得,适合热加工的工艺区间主要为950℃~1080℃、0.1~10 s−1、1040℃~1080℃、0.01~0.1 s−1和1130℃~1150℃、0.01~0.1 s−1。
3.5. 微观组织
热加工图对实际生产具有参考意义,但并不能完全精准预测,还需对显微组织进行验证。图8(a)~(c)为变形温度1050℃、变形速率分别为0.01、0.1和1 s−1的热压缩后显微组织;图8(d)和图8(e)为变形速率0.01 s−1、变形温度分别为1100℃和1150℃的热压缩后显微组织。对于发生了部分再结晶的试样,即使快冷后无法将等轴再结晶奥氏体晶粒保留至室温,但形貌可保留至室温,如图8(a)~(c)所示。热压缩后组织被拉长,在变形温度为1050℃压缩变形时试样发生了再结晶,生成等轴无畸变的奥氏体小晶粒,在快速冷却后,再结晶晶粒会发生马氏体转变生成马氏体,且在此过程中不会发生晶粒长大,故形貌仍

Figure 7. Hot processing map of EH460 steel under different strain (a) 0.2; (b) 0.4; (c) 0.6; (d) 0.8
图7. EH460钢在不同应变量下的热加工图(a) 0.2;(b) 0.4;(c) 0.6;(d) 0.8

Figure 8. Microstructure of the sample under different deformation conditions. (a) 1050˚C, 0.01 s−1; (b) 1050˚C, 0.1 s−1; (c) 1050˚C, 1 s−1; (d) 1100˚C, 0.01 s−1; (e) 1150˚C, 0.01 s−1
图8. 不同变形条件下试样的显微组织。(a) 1050℃,0.01 s−1;(b) 1050℃,0.1 s−1;(c) 1050℃,1 s−1;(d) 1100℃,0.01 s−1;(e) 1150℃,0.01 s−1
可保留,所以在光学显微镜下可观察到被拉长的晶界周围有一些小晶粒,其本质为保留了热压缩后未快速冷却前的再结晶晶粒形貌的马氏体。
图8(a)~(c)中组织基本为马氏体,且均可观察到存在再结晶晶粒的形貌,且再结晶晶粒形貌尺寸逐渐减小,主要是因为在相同变形量时,压缩速率大则变形时间短,再结晶晶粒来不及形核长大。图8(a)、图8(d)和图8(e)中,组织均存在马氏体,与图8(d)相比,图8(a)和图8(e)均观察到再结晶晶粒形貌,但图8(e)中的数量较少,原因为在该变形条件下发生了二次硬化;在图8(d)中出现了严重的组织不均匀现象,组织为马氏体和铁素体,可能原因为该区域在热压缩过程中温度不均匀导致发生不同的相变,这在热加工过程中应尽量避免。
4. 结论
通过对EH460钢在变形温度为900℃~1150℃、变形速率为0.01~10 s−1条件下进行热压缩试验,分析了EH460钢的热变形行为和热加工图,得到主要结论如下:
1) EH460钢的热变形行为主要受加工硬化、动态回复和动态再结晶控制,真应力–真应变曲线也表现出不同的变形机制,且流变应力随变形温度的增大而减小,随变形速率的增大而增大。
2) 通过建立EH460钢的本构方程,计算出在不同变形条件下的预测值,将其与试验值进行对比,R值为0.994,AARE值为4.498%,相关性较好。
3) 基于DMM模型分析了EH460钢在不同应变量下的热加工图,并通过观察不同变形条件下的显微组织进行验证,适合热加工的工艺区间主要为950℃~1080℃、0.1~10 s−1、1040℃~1080℃、0.01~0.1 s−1和1130℃~1150℃、0.01~0.1 s−1。