基于BP神经网络的抗乳腺癌候选药物预测

Prediction of Anti-Breast Cancer Drug Candidate Based on BP Neural Network

摘要: 目前，乳腺癌已成为世界上致死率最高的癌症之一。据研究表明，通过调节雌激素受体亚型(ERα)活性可以控制人体内的雌激素水平，人体内的雌激素水平与乳腺癌的发展密切相关。而利用可以拮抗ERα活性的化合物有极大的可能可以治疗乳腺癌疾病，比如，临床治疗乳腺癌的经典药物他莫昔芬和雷诺昔芬就是ERα拮抗剂。本文基于化合物对ERα活性和化合物分子描述等已有数据，建立一个用于预测化合物对ERα生物活性的定量预测模型，然后利用随机森林和皮尔逊相关系数对影响生物活性最大的变量进行筛选降维，利用降低维数后的变量，搭建BP神经网络，构建预测模型。最后通过测试得到我们的模型预测效果好，泛化能力强，不容易发生过拟合。并对所提出的预测模型进行展望与分析。

Abstract: Breast cancer has become one of the world’s most deadly cancers. Studies have shown that estrogen levels in the human body, which are closely associated with the development of breast cancer, can be controlled by regulating the activity of the estrogen receptor sub-type (ERα). Therefore, the use of compounds that antagonize ERα activity has great potential to treat breast cancer diseases. For example, tamoxifen and raloxifene, the classic drugs in clinical treatment of breast cancer, are ERα antagonists. Based on compounds of ER alpha activity and molecular description of existing data, set up a used to predict compounds quantitative prediction model of ER alpha biological activity, and then use random forests and Pearson correlation coefficient of the biggest variables to affect the biological activity screening dimension reduction, after using the lower dimension variable and building a BP neural network, forecast model was constructed. Finally, through testing, our model has good prediction effect, strong generalization ability is not prone to overfitting. The prediction model is prospected and analyzed.

1. 引言

癌症是指起源于上皮组织的恶性肿瘤，而根据目前有关数据及研究表明，乳腺癌是当前世界上最常见且致死率较高的癌症之一，据2020年世界卫生组织国际癌症研究机构(IARC)最新数据显示，全球范围内乳腺癌新增人数大约为226万，其发病率首次超过肺癌成为全球第一大癌症。有关研究表明，雌激素受体α亚型(Estrogen receptors alpha, ERα)在乳腺发育过程中扮演了十分重要的角色 [1] [2]。

在医学上，通常抗激素治疗常用于ERα表达的乳腺癌患者，其目的是通过调节雌激素受体活性来控制体内雌激素水平。因此，ERα被认为是治疗乳腺癌的重要靶标，能够拮抗ERα活性的化合物可能是治疗乳腺癌的候选药物。但是在实际的药物研发是困难重重的，在研发过程中需要对时间以及成本进行合理的控制，一般倾向于采用建立化合物活性预测模型的方法来筛选潜在活性化合物，从而使得模型具有更好的预测效果。具体的做法是：首先，针对与疾病相关的某个靶标(这里指定为雌激素受体α亚型)，收集并且整理一系列作用于该靶标的化合物及其生物活性的数据，然后以一系列分子结构描述符作为自变量，化合物的生物活性值作为因变量，构建化合物的定量结构–活性关系(Quantitative Structure-Activity Relationship, QSAR)模型，最后使用得到的模型预测具有更好生物活性的新化合物分子，或者指导已有活性化合物的结构进行优化。

为了提高预测的效果，一般来说会使用比较大的数据集进行训练和测试，而面对复杂的高维数据，通常不太利于我们进行有效的分析。本文大致分为两部分，第一部分利用两种合适的方法对已有数据集进行有效的降维，第二部分是利用降维后的数据对进行预测模型的搭建训练、优化以及测试，最后一部分用得到的模型对已有的测试集进行测试体现模型的高效性和有效性。对于数据降维方法来讲，常用的有主成分分析(PCA) [3] [4]、随机森林 [3] [5] 和皮尔逊相关系数 [6] 等都可以作为降低变量维数的方法，但是仅用一种方法进行筛选容易产生偶然性的结果，那么我们就考虑将两种合适的降维方法进行有机的结合，这样即可以有效的将高维数据降维同时也可以一定程度上避免偶然性的结果。对于第二部分建立预测模型而言，随着人工智能的迅速发展，BP神经网络 [7] [8] [9] [10] 作为应用最广泛的神经网络之一，在模型预测 [8] [9] [10] 方面的研究也逐渐增多，并在实际应用中取得优秀的表现。基于上述研究，本文采用神经网络对建立的预测模型进行训练并测试。

2. 相关基础知识及模型建立

2.1. 基础知识

随机森林是一种Bagging算法 [3] [5]，这类算法通过训练多个弱模型打包组成一个强模型，可以在提高模型准确率和稳定性的同时，通过降低结果的方差来避免过拟合的发生。因此，强模型的性能很大程度上会优于弱模型，而在随机森林中弱模型选取的是决策树。在数据训练阶段，随机森林使用bootstrap从训练数据集中采取多个子训练数据集训练多个不同的决策树，预测阶段采取各个决策树预测结果的平均值。在训练决策树模型时，需要考虑如何选择切分变量、切分点及其衡量他们的好坏。本文采用平方平均误差作为不纯度函数，则针对某一切分点 $G\left(x,v\right)$ 有：

$G\left(x,v\right)=\frac{1}{N_s}\left({\displaystyle \underset{y_i\in X_{left}}{\sum }{\left(y_i-{\bar{y}}_{left}\right)}^2}+{\displaystyle \underset{y_i\in X_{right}}{\sum }{\left(y_i-{\bar{y}}_{right}\right)}^2}\right)$ (2-1)

随机森林算法中，特征重要性指特征对预测结果的影响程度，某一个特征重要性越大，标明该特征对预测结果的影响越大。本题求解过程中采用sklearn内部树模型计算建模中729个变量的重要性，第i个节点的重要性为：

$n_i=w_i\ast G_i-w_{left}\ast G_{left}-w_{right}\ast G_{right}$ (2-2)

其中， $w_i,w_{left},w_{right}$ 分别为节点i以及其左右子变量中训练样本个数与总训练样本数目的比例， $G_i,G_{left},G_{right}$ 分为变量i以及其左右子节点的不纯度。则某一变量的重要性为：

$f_t=\frac{{\displaystyle {\sum }_{j\in t变量t的切分节点}{n}_j}}{{\displaystyle {\sum }_{i\in 所有节点}{n}_i}}$ (2-3)

为了确保所有变量的重要性总和为1，对每个变量的重要性进行归一化操作，即公式(2-5)：

$f_{nt}=\frac{f_t}{{\displaystyle {\sum }_{j\in 所有变量}{f}_j}}$ (2-4)

皮尔逊相关系数(Pearson Product-Moment Correlation Coefficient, PPMCC)用于度量两个变量X和Y之间的相关程度，其值介于−1与1之间 [6]。相关系数的绝对值越大，则表明X与Y相关度越高。

两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和他们各自标准差乘积的商，相关系数又称“皮尔逊相关系数r”。计算公式如下：

${\rho }_{X,Y}=\frac{\mathrm{cov}\left(X,Y\right)}{{\sigma }_X{\sigma }_Y}=\frac{E\left(\left(X-{\mu }_X\right)\left(Y-{\mu }_Y\right)\right)}{{\sigma }_X{\sigma }_Y}=\frac{E\left(XY\right)-E\left(X\right)E\left(Y\right)}{\sqrt{E\left(X^2\right)-E^2\left(X\right)}\sqrt{E\left(Y^2\right)-E^2\left(Y\right)}}$ (2-5)

其中E是数学期望， $\mathrm{cov}\left(X,Y\right)$ 表示X与Y的协方差。

2.2. 模型建立

根据已知条件(本文所使用的数据集文件均来自2021年中国研究生数学建模竞赛附件，附件一和附件二分别为“Molecular_Descriptor.xlsx”和“ERα_activity.xlsx”)，构建模型自变量 $X=\left[X_1,X_2,X_3,\cdots ,X_{729}\right]\in R^{1974\times 729}$。其中 $X_i$。表示文件1中提供的1974个化合物的第i个分子描述符。根据题意，化合物对ERα的生物活性值的负对数(即pIC₅₀值)作为本次建模的因变量 $Y\in R^{1974\times 1}$。通过自变量X和因变量Y构建数学模型如等式(2-6)所示：

$Y=F\left(X\right)$ (2-6)

其中， $X_l,X_r$ 表示左右子节点的训练样本集合， $N_s$ 为当前节点所有训练样本个数， $y_i$ 指当前节点， ${\bar{y}}_i$ 指当前节点样本目标变量的平均值。

3. 模型求解

3.1. 数据降维

通过应用2.1中的随机森林算法，我们对729个变量应用上述随机森林回归预测模型，选取出前40个变量及其特征重要性值如表1：

Table 1. The forty main variables and characteristic importance

表1. 40个主要变量及特征重要性

进一步对经过随机森林获得的40个变量采用皮尔逊相关系数进行检验，分别计算出两个变量之间的皮尔逊相关系数绝对值，计算公式采用公式(2-5)，图1表示40个变量之间的皮尔逊系数热力图。

Figure 1. Pearson coefficient thermal diagram between forty variables

图1. 40个变量之间的皮尔逊系数热力图

其中，颜色越浅标明两个变量之间的相关性越小，颜色越深标明两个变量的相关性越大。可以看到大部分变量间的相关性较弱，我们将相关性强的变量进行剔除，最终筛选出20个变量。如表2所示：

Table 2. The twenty molecular descriptors with the most significant effect on biological activity

表2. 20个对生物活性最具有显著影响的分子描述符

3.2. 基于BP神经网络的预测模型

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，网络是由输入层、隐藏层和输出层组成，隐藏层可以是一层或多层，一般的BP神经网络模型结构如图2所示。在表2中，我们以前17个分子描述符对于化合物的影响指标作为输入，所以输入层的节点数为17，输出节点为化合物的对ERα的生物活性值pIC₅₀，因此输出节点数为1。隐藏层的节点设置在网络模型的训练过程中至关重要，隐藏层的节点数过多会增加网络计算的复杂度并出现过拟合现象；如果隐藏层节点数太少，则会影响模型性能，无法达到期望的效果。本文在选取隐藏层的节点数时参考了以下公式：

$l=\sqrt{n+m}+a$ (3-1)

其中l表示隐藏层节点个数，n为输入层节点个数，m为输出层节点个数，a表示取值范围为[1,10]之间的常数。网络通过反向传播函数不断调节网络权值和阈值，使误差损失达到极小。使用BP神经网络模型的建立流程如图3所示：

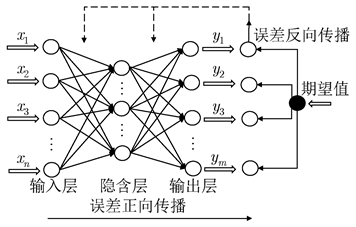
Figure 2. Schematic diagram of BP neural network structure

图2. BP神经网络结构示意图

Figure 3. The establishment process of BP neural network

图3. BP神经网络的建立流程

3.3. 实验结果及分析

本文所有实验都在Matlab2020a下进行。在由于各变量的数值范围有很大的差异，在训练过程中会出现消耗的时间较长，收敛速度较慢等问题。导致最终获得的目标值波动范围较大的数据可能会偏大，波动范围较小的数据可能会偏小。为了缓解以上问题，我们在将数据通入BP网络前，先对数据进行归一化处理。由于在网络的输出层我们采用了Sigmoid函数作为激励函数，因此在数据归一化过程中，我们将数据统一归一到[0,1]区间。本次实验过程中采用Matlab内置函数normalize()将数据标准化[0,1]区间。本文搭建网络时，将数据划分为训练集、验证集和测试集，三类集合分别选择附件一训练集的70%、15%和15%作为数据样本，选取4个隐藏层，各个隐藏层节点数分别为：100，70，50，40。学习率设为0.001，迭代500次。具体如图4为网络训练基本过程和图5为模型仿真图所示：

Figure 4. BP neural network training process

图4. BP神经网络训练过程

Figure 5. Model simulation diagram

图5. 模型仿真图

经过不断的训练我们结合图5可以看出，模型的均方误差随着迭代次数的增加是在减少的，训练集与测试集的误差会逐渐减少，当神经网络训练达到140次代时，三条曲线几乎重合，误差也随之稳定。因此我们根据上述的结果选择上述搭建的网络以及设置的参数进行测试。

为了避免偶然性，我们重新选择1274个数据作为训练集，500个数据作为测试集，使用BP神经网络模型，将最终得到的目标值和预测值进行对比，最终我们所得到的目标值和预测值的对比图如图6所示：

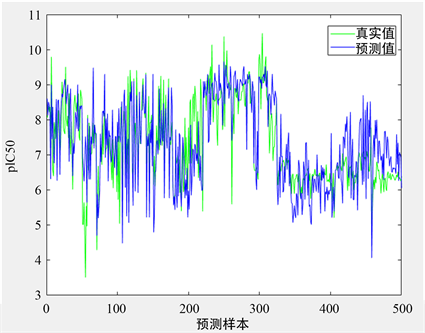
Figure 6. Comparison of actual and predicted values

图6. 真实值与预测值对比图

通过以上的训练及测试的实验结果说明我们所采用的BP神经网络对化合物对ERα生物活性的预测效果好，误差较小且泛化能力强。

4. 总结

本文以抗乳腺癌药物候选预测为目标，用随机森林和皮尔逊相关系数的组合，对已知高维数据集进行有效的变量降维，进一步利用BP神经网络以筛选出的变量构建药物候选预测模型，并通过自适应学习率动量梯度下降法不断优化模型，从而得到较优的预测模型，在训练集和测试集均表现良好。但由于数据集较为有限，方法使用较为单一，一种方法我们将考虑加大数据量并结合不同的预测方法来进一步改善模型，第二种方法我们会考虑将非凸正则项加至目标函数中，不使用传统的降维方法，从而也可以使得结果的稀疏性得以更好的保证，进一步进行大量的数值试验来验证我们的想法。