1. 引言
2019年7月24日至27日,由教育部高等学校大学物理课程教学指导委员会、教育部高等学校物理学类专业教学指导委员会、中国物理学会物理教学委员会主办的“2019年全国高等学校物理基础课程教育学术研讨会”和“2019年全国高等学校物理基础课程青年教师讲课比赛决赛”在云南师范大学呈贡校区隆重举行。根据教育部高等学校大学物理课程教学指导委员会和教育部高等学校物理学类专业教学指导委员会的活动规划和安排,今年的青年教师讲课比赛的课型为实验课教学的角逐。
在本次活动的讲课比赛环节中,有参赛选手展示的迈克尔逊干涉仪实验课教学(浓缩课)引起了与会人员特别是参赛教师和评委专家组的广泛讨论和争议。其中,最为典型和突出的有三个问题:
1) 迈克尔逊干涉是属于杨氏干涉还是属于等倾干涉?
2) 迈克尔逊干涉仪中的补偿板是否是必须的?
3) 迈克尔逊干涉的实验光路图应该是单线光路还是复线光路?
这些问题反映出长期的教学及实践工作中,对迈克尔逊干涉仪的个别元部件的作用的认识还存在一定的分歧。同时,对光的干涉涉及到的一些概念的提法也还存在观点不甚统一。
本文从光的干涉的基本原理出发,将涵盖迈克尔逊干涉仪及其干涉中的这些问题作比较细致的梳理,仅供参考与进一步讨论。
2. 光的干涉原理
首先说明;本文中所涉及的光的传播介质,在没有特别标定或指出的情况下都均视为真空。

Figure 1. The principle of interference of light
图1. 光的干涉原理
光的干涉是指满足一定条件(频率相等、相差恒定、光矢量即电场强度矢量振动方向相同) [1] 的两列或多列光波在空间相遇时相互叠加,在某些区域始终加强,在另一些区域则始终削弱,形成稳定的强弱分布的现象。设如图1所示的两相干光源S1和S2的振动方程分别为:
(1)
(2)
那么,它们分别在光场中的某一点P引起振动的振动方程分别为:
(3)
(4)
与
的合成的振动方程为:
(5)
其中,合成振动的振幅及初相位分别为:
(6)
(7)
由于,两振动
与
的相位差为:
(8)
显然,若P点给定,则
恒定,即
取决于两光源S1和S2到P点的光程差
,从而结合(6)式可知,光场中每一点的合成振动的振幅A保持恒定。因此也就说明,两相干光源S1和S2的两振动在光场中激发的两列光波形成稳定强弱分布的干涉现象。
现从最简单的情况
分析,结合图1不难看出,这时
。因此,根据(6)式,当
,即
(9)
时,合成振动的振幅最大,呈现干涉相长,表现出明条纹。这时
(10)
而当
,即
(11)
时,合成振动的振幅最小,呈现干涉相消,表现出暗条纹。这时
(12)
在实践实验中,可以采取不同的途径和方法获得相干光源(或相干光束),广泛实现不同环境及不同条件下的光的干涉,以达到为实验教学和科学研究服务的目的。
3. 两个典型的光的干涉实例
3.1. 杨氏干涉
1801年,英国物理学家托马斯·杨(1773~1829)在实验室里首次成功地观察到了光的干涉。如图2所示是托马斯·杨的实验 [2] 光路,他采用烛光作为光源,烛焰、单缝、双缝和光屏等关于轴线SO对称。其中,单缝的作用是获得线光束,双缝的作用是获得振动情况完全相同的相干光束,图中双缝S1与S2之间的距离d以及
角在实际实验装置或实验中都是很小的。
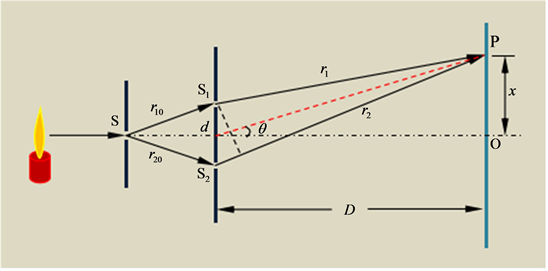
Figure 2. Optical path of Young’s interference experiment
图2. 杨氏干涉实验光路
设由光源发出的光先后经过单缝和双缝形成的两束相干光束投射到光屏上的P点,那么这两束光的光程差为:
(13)
根据光的干涉原理,当
(14)
时,可得相应的明暗条纹位置为:
(15)
容易得出,相邻两条明条纹或相邻两条暗条纹之间的距离即条纹间距为:
(16)
特别说明:托马斯·杨的这一双缝干涉实验简称杨氏双缝干涉实验,它是物理学史上最美丽的十大实验 [3] [4] 之一,其巧妙之处主要就在于用一个普通而简单的双缝就轻松的获得了相干光束,这种获得相干光束的方法称为分波阵面法。托马斯·杨利用双缝干涉实验首次成功地观察到了光的干涉,为光的波动性奠定了坚实基础和提供了有力证据。
3.2. 薄膜干涉
光源发出的光投射到透明薄膜(厚度在毫米量级以下)的分界面时将分为两部分,一部分光经薄膜外表面反射回与入射光场同侧的反射光场,另一部分光经薄膜外表面折射进入薄膜再经薄膜内表面反射后又再经薄膜外表面折射回反射光场。这时在薄膜外表面附近乃至广阔的空间会产生经薄膜的两个表面反射的两列反射光束的干涉现象,即所谓的薄膜干涉。
关于光的任何形式干涉的计算,最基本的计算都是光程差的计算。而在薄膜干涉中,光程差的计算方法并不唯一 [5] - [12],这里仅介绍其中一种。如图3所示,假设一束一定频率的光线a投射到厚度为d、折射率为n的薄膜外表面,经薄膜反射、折射后分割成两束光线a1和a2。由于光由光疏介质投射到光密介质发生反射时将产生半波损失,故光线a1在A点产生半波损失。因此,光线a1与光线a2的光程差可表示为:

Figure 3. Thin-film interference optical path
图3. 薄膜干涉光路
(17)
根据折射定律和几何关系:
(18)
可将(17)式化为:
(19)
光线a1与光线a2发生干涉的明暗条纹满足的条件:
(20)
在薄膜干涉中,空间介质结构一定时,光程差
与薄膜厚度d和入射光线的入射角i有关。当入射角i一定(比如
)而薄膜厚度d不均匀时,薄膜厚度相同的位置将产生同级干涉条纹,即等厚干涉,如图4所示;

Figure 4. Equal-thickness interference of thin-film surface
图4. 薄膜表面的等厚干涉

Figure 5. Equiclinal interference at infinity
图5. 无线远处的等倾干涉
当薄膜厚度d均匀而有不同入射角i (或入射光线的倾斜角)的入射光时,入射角相同的光线将产生同级干涉条纹,即等倾干涉,如图5所示。
在科学实践中,等厚干涉和等倾干涉都有着广泛的重要应用 [5] [6] [7] [8]。
这里说明一下光的分振幅法。由于光的能量跟光的振幅平方成正比,故将像薄膜干涉中这种分割光束的方法称为分振幅法。因此,薄膜干涉是利用光的分振幅法获得相干光束的。
4. 迈克尔逊干涉仪和迈克尔逊干涉
4.1. 迈克尔逊干涉仪结构
迈克尔逊干涉仪,是1881年美国物理学家阿尔伯特·亚伯拉罕·迈克尔逊和莫雷·爱德华·威廉姆斯合作设计制造的精密光学仪器。通过调整该干涉仪,可以产生等厚干涉条纹,也可以产生等倾干涉条纹。迈克尔逊干涉仪的结构如图6所示。其中,M1和M2是一对精密的相互垂直的平面镜,可通过它们的调节螺钉调节两者之间的垂直度,且M1可沿导轨前后调动,M2固定。G1和G2是厚薄及折射率得均匀程度都很高的相互平行放置的相同玻璃板,且G1的背面镀有一层很薄的银膜,起到分割光束作用,称为分光镜;G2起补偿光程作用,称为补偿板。同时,M1和M2所在平面分别与G1和G2所在平面之间均成45˚夹角。
4.2. 迈克耳逊干涉原理
迈克耳逊干涉仪是利用分振幅法产生双光束以实现干涉,即让一束入射光经过分光镜分为两束相干光后各自被对应的平面镜反射后发生干涉。通过调节干涉臂长度或改变介质的折射率可以实现两束相干光的不同光程,同时,通过调节反射镜M1和M2的调节螺钉可以轻微改变它们之间的垂直度,从而能够形成不同的干涉图样。
如图7所示是迈克尔逊干涉的光路图,图中
是M2在M1中的虚像。光源发出的光束经分束镜G1分成光束1和光束2。其中,光束1先后三次通过G1,而光束2通过一次通过G1两次通过补偿板G2,这样就避免两光束所经过路程不同而引起较大的光程差。
从观察角度看,两相干光束可视为光束1和光束2分别从M1和
的反射光束,迈克尔逊干涉就相当于M1与
的“空气薄膜”形成的薄膜干涉。若设“空气薄膜”的厚度为d,光束1入射“空气薄膜”的入射角为i,同时注意到光束1与光束2分别在G1和G2表面反射产生半波损失引起的额外程差相互抵消。因此,迈克尔逊干涉的光程差为:
(21)
因此,光束1与光束2发生干涉的明暗条纹满足的条件为:
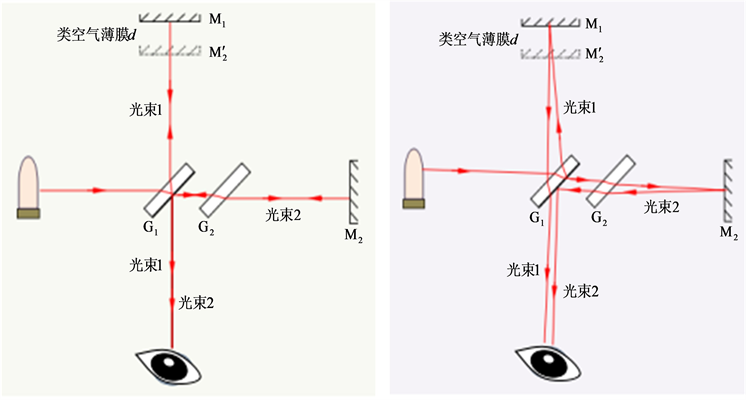 (a) 入射光束与分光镜严格成45˚角 (b) 入射光束与分光镜不严格成45˚角
(a) 入射光束与分光镜严格成45˚角 (b) 入射光束与分光镜不严格成45˚角
Figure 7. Michelson interference optical path
图7. 迈克尔逊干涉光路
(22)
其中,当
或
但
时,其光路分别对应图7中的(a)和(b)。
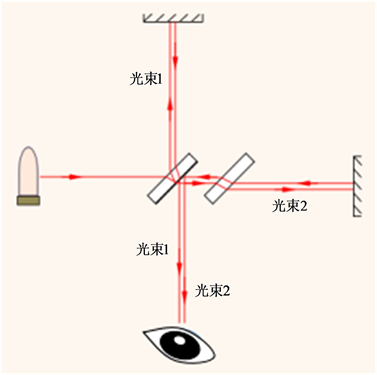
Figure 8. Michelson interference conventional error optical path diagram
图8. 迈克尔逊干涉惯用错误光路图
这里附带说明一下,目前的一些教材 [13] 亦或课堂教学过程中,迈克尔逊干涉常出现如图8所示的错误光路图形,容易误导,应予以修正。
理论与实践研究表明,迈克尔逊干涉的类型跟M1与M2之间的垂直度或M1与
平行度有关系 [14],即
1) 当M1垂直M2或M1平行
时,产生等倾干涉,条纹间距随着M1与
之间的距离减小而增大。
2) 当M1不严格垂直M2或M1与
之间存在微小夹角时,产生等厚干涉,条纹形状跟M1与
之间的夹角决定。
5. 结论
通过比较迈克尔逊干涉与杨氏干涉、薄膜干涉获得相干光束的方法和特点,以及对迈克尔逊干涉原理的较深入理解,可以得到以下结论:
1) 迈克尔逊干涉与薄膜干涉都是采用分振幅法获得相干光束,而杨氏干涉是采用分波阵面法获得相干光束。但迈克尔逊干涉与杨氏干涉或薄膜干涉在概念上没有相互兼容性,因此,关于迈克尔逊干涉是否属于杨氏干涉或薄膜干涉的提法是极不妥当的。
2) 迈克尔逊干涉仪具有既能产生等倾干涉也能产生等厚干涉的特点,因此,不能简单地将迈克尔逊干涉定论为等倾干涉或等厚干涉。
3) 迈克尔逊干涉仪实现干涉过程中,补偿板的作用是避免两相干光束之间出现较大的光程差。但在实践实验中,通过调节干涉臂长度也可以实现两相干光束的不同光程,因此,没有补偿板同样也可以达到所需要求。
4) 迈克尔逊干涉光路并不唯一,至于是单线光路[比如图7(a)]还是复线光路[比如图7(b)],要根据入射光束跟分束镜等元件之间的位置精密关系的实际情况才能确定,但要避免图8类似的光路。