1. 引言
极限是微积分学的精髓,数学分析中的重要概念如连续、导数、定积分、无穷级数的敛散性、广义积分的敛散性等等都是通过极限定义的。多元函数的极限是多元函数微积分学中的重要基本概念。它与一元函数的极限类似,但因多元函数的自变量比较多,这使得二者之间既紧密联系又有很大差别。学生在初次学习这些内容时,很难比对出、分析出它们本质上的异同。且大多的数学分析教材只是将多元函数极限的计算作为一元函数极限计算方法的推广,没有系统的、深入的研究。因此多元函数极限的计算及其存在性的判断备受学者的关注和青睐。
早在1997年王丽芳 [1] 通过构造不同的曲线族来说明二元函数极限的不存在,但该方法不能用来判定极限存在的情形。四年之后梁小林 [2] 利用构造法求趋近曲线,并给出了判别多元函数极限不存在的简单条件,得到了其极限不存在的直接判别法。闻卉 [3] 介绍了如何利用同阶无穷小量判断二元函数极限的不存在。郑军和吴元泽 [4] [5] 也先后讨论了类似问题。慢慢地,人们对多元函数的极限有了更深入的研究。2018年熊允发 [6] 和杜玉平 [7] 结合教学实践与体会,探究了求二元函数极限的若干方法。2019年张瑞芳和王海军 [8] 给出了一类特殊二元函数极限存在的充要条件。2020年毛一波 [9] 探讨了三元函数的混合极限与三次极限的关系,研究表明,它们的存在性没有必然的蕴含关系。同年,刁露等人 [10] 讨论了二元函数在圆邻域以及方邻域上的极限求解及其连续的应用。张志会、李丽红等诸多学者也对此问题进行了相关研究 [11] - [16]。田振明 [17] 等人基于n元函数的泰勒公式,分析其在求多元函数极限问题时的适用情形与条件。尽管他们研究的内容不完全相同,但有相似之处,他们都侧重讨论多元函数极限不存在的判别方法及其存在时的求解方法,较少涉及多元函数极限存在的证明。目前仅有阎明刚 [18] 于1988年在商丘师专学报上发表了《用定义证明多元函数极限的一个方法》,他利用代数方法(多项式带余除法)证明多元多项式的极限存在,但该方法具有一定的局限性。
因为多元函数的极限本身就非常复杂,且其存在性的证明又是一个难点,所以这让很多学生感到茫然,束手无策,无从下手。鉴于此,很有必要系统地、详细地研究如何用定义证明多元函数的极限。本文在前人研究成果的基础上,首先着重分析二元函数极限的定义;其次,结合典型例题,通过预控法限定变量x和y的取值范围,根据二元函数极限的不同形式,选用放大法或缩小法对不等式进行放大或缩小;最后借助函数极限的
语言给出严谨的证明过程。
2. 准备知识
本文所用到的概念,详细内容可参看文献 [19] [20] [21]。
定义1设D是
上的开集,
为一定点,
是定义在
上的二元函数,A是一个实数。如果对于任意给定的
,存在
,使得当
时,成立
。则称当
时,函数
收敛,并称A为
当
时的极限,或者
在点
的极限为A。记为
。这里
表示以
为心,
为半径的去心邻域,即
。
注1如何理解二元函数极限的定义呢?从以下三个方面进行分析。
1) 如何理解
?
回顾一元函数极限的
定义。
:
,
,
:
。
这里自变量x只能沿x轴从
的左侧或右侧趋于
时,
都无限接近于A。

写出二元函数极限的
定义。
:
,
,
:
。
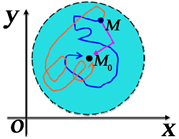
这里M在
的去心
邻域内,
表示M以任意方式(沿直线,曲线等所有方式)趋于
时,
都无限接近于A。
2)
的等价表示形式;
a)
,这里
表示M与
之间的距离,其中
。
b)
,
,对
满足
,
,且
。
3) 二元函数极限的书写形式;
在
中,点列
等价于
,
,故
可写成
这种形式。从这个角度来看,二元函数
在点
的极限为A,也称
在点
的二重极限为A。
注2如何用定义证明二元函数的重极限
?
与一元函数极限类似,用定义证明重极限存在时,采用放大法。记
,
,对刻画函数极限过程的量
放大,分离出刻画自变量变化趋势的项
,而
较复杂,不易直接分离出该形式,我们退而求其次,分离出
和
,结合
,
,即可将
和
转化为
的形式。故要证明
,即证:对任意给定的
,找到一个合适的
,使得当
时,成立
,
这里
,
,令
,求出
,即可确定出
。
思考1这里的
唯一吗?
以上讨论了二元函数的重极限(自变量趋于某个定点,极限值是某个确定的数),还有一类极限,非正常极限:极限值为无穷大或者是无穷远处的极限(自变量趋向于无穷远处),无穷又分为正无穷、负无穷、无穷。对于n元函数,有n个自变量,自变量趋于无穷远处时,可以是某个自变量趋于无穷远处,也可以是多个自变量趋于无穷远处,因此多元函数的非正常极限有不同的形式。这里仅以一种形式给出定义。
定义2设D是
上的开集,
为一定点,
是定义在
上的二元函数。对任意的实数
,存在
,使得当
时,成立
。则称当
时,函数
发散到无穷,记为
。
定义3设A是一个实数,若对任意给定的
,存在
,使得当
,
时,成立
。则称A为函数
当
时的极限,记为
。
注3如何用定义证明二元函数的非正常极限呢?以
例进行说明。
要证明
,即证:对任意的实数
,找到一个合适的
,使得当
时,成立
。与证明
的方法类似,用定义证明
时,采用缩小法。记
,
,对刻画函数极限过程的量
缩小,分离出刻画自变量变化趋势的项
。故要证
,即证:对任意的实数
,找到一个合适的
,使得当
时,成立
,
这里
,
,令
,求出
,即可确定出
。
3. 实例分析
例 用定义证明。
1)
;2)
;
3)
;4)
。
证明1) 记
,
,
,
要证:对任意给定的
,找到一个合适的
,使得当
时,
。现
,对
进行放大,要分离出
,只须分离出
和
形式。则
当
时,
比较小,利用预控法来控制变量x和y,不妨设
,此时
,
令
,求出
,取
,则当
时,有
。
2) 记
,
,
,
要证:对任意给定的
,找到一个合适的
,使得当
时,
。
现
,因
,且当
时,分母
,分子
,即分母是有界量,分子是无穷小量,也就是说要使不等式
,
在这个极限过程中,分子起着主要作用,故仅需对分子进行变量分离,分离出
和
形式,将分母放缩为有界量(不能为零);则有
当
时,
比较小,利用预控法来控制变量x和y,不妨设
,此时
,
,可得
,从而有
,
令
,求出
,取
,则当
时,
。
3) 记
,
,
,
要证:对任意的
,找到一个合适的
,使得当
时,
。
现
,因
,且当
时,分母
,分子
,即分子是有界量,分母是无穷小量,也就是说要使不等式
,在这个极限过程中,分母起着主要作用,故仅需对分母进行变量分离,分离出
和
形式,将分子缩小为有界量(不能为零);则有
;
当
时,
比较小,利用预控法来控制变量x和y,不妨设
,此时
,
,可得
,从而有
,
令
,求出
,取
,则当
时,
。
4) 要证:对任意的
,找到一个合适的
,使得当
,
时,
。
函数结构中含有因式
,类比已知
,为此进行形式统一,对
放大,即
因
,故对
,存在
,当
时,
。取
,当
,
时,
,此时,
。
思考2利用预控法来控制变量x和y时,在题目(1) (2) (3)中,分别不妨设
,
,
,这里的1,
,
是如何得到的?这些值可随意选取还是受某些因素的制约?
4. 结束语
这里以四个题目为载体,介绍了预控法在二元函数极限证明中的应用。在实际的教学过程中,学生必须做足够数量的练习题,才能深刻理解和领悟多元函数极限的本质。练习用定义证明多元函数的极限,这有助于提高学生分析问题的能力和严谨的逻辑推理能力。
然而在实际中,多元函数极限在形式上非常复杂;学生在学习过程中要注意积累证明方法和技巧,在求解某个具体极限问题时,抓其本质特征,在变中找不变,选择合适的方法进行求解。
多元函数的极限是数学分析的核心内容之一,是数学家在漫长的历史过程中从事科学研究的成果体现,不仅在知识体系上博大精深,而且在内容中蕴含着丰富的数学思想和数学方法。这些数学方法和数学思想对培养学生的思维观和方法论起着非常重要的作用。
NOTES
*通讯作者。