1. 引言
随着我国交通事业长期快速发展,公路隧道的建设发展也愈来愈快。在高速公路隧道建设至运营后,二次衬砌作为重要结构组成部分,极大影响隧道整体结构安全性,二次衬砌结构的安全因素成为国内外学者关注的焦点。隧道二次衬砌的安全性影响规律以及隧道安全性影响变化的研究也会有着重要意义,其中隧道衬砌结构灵敏度及线性相关性分析可以探究隧道衬砌结构的影响因素及其影响规律。在国内外,在隧道二次衬砌相关灵敏度研究领域中,余永康 [1] 针对深埋软弱围岩,采用“荷载–结构”构建隧道模型,通过对二次衬砌灵敏度分析,得出因为隧道衬砌截面厚度的不同,每个截面的偏心率会显著变化,其离散率较大、变异性大;且衬砌厚度的增大也会导致截面轴力与弯矩的增长速率起伏变大。Henrique M.等 [2] 针对隧道衬砌的几种失效模式计算了解决方案,通过对FORM计算单个故障模式的解,利用蒙特卡罗模拟技术对系统可靠性计算,得出FORM方法在估计个体失效概率方面是非常有效的,还表明重要性抽样蒙特卡罗是非常有效的。杨建宏 [3] 采用蒙特卡洛法为主的统计分析方法,针对衬砌厚度的分布规律分析了二次衬砌在设计标准的条件下,基于隧道计算模型,使用安全系数法计算衬砌厚度对其产生影响程度。黄华南 [4] 利用蒙特卡洛法,探究影响衬砌可靠性的主要原因,并针对二次衬砌厚度进行进一步分析,得出衬砌厚度对结构可靠性影响规律。张显达 [5] 基于隧道有限元分析模型,通过对初期支护以及二次衬砌进行影响分析,得出隧道的安全性受初期支护以及二次衬砌厚度的影响最大。
本文依托实际高速公路隧道工程,通过整理参考相关资料和规范,拟采用蒙特卡罗法分析衬砌结构的灵敏度及线性相关性,蒙特卡洛法是随机抽样数理计算方法,通过该方法对可能影响隧道二衬结构的主要因素进行大量抽样,得到大量抽样计算数据,通过PDS技术分析可以得到影响二次衬砌结构安全性的随机变量分布规律和概率分布,并对二次衬砌的灵敏度、相关输出变量线性相关性进行定量、定性分析,得出二次衬砌结构的最大影响因素及其影响规律,此方法所得结果直接、清晰、准确,且该方法应用性强,可使用计算机进行大量数据计算。在隧道衬砌结构灵敏度分析中涉及很多随即参数相关运算,包括隧道衬砌弹性模量、衬砌厚度等,运用蒙特卡洛法原理,将随机参数进行大量的统计运算,计算相关函数分布,能够获得相对应的概率特征分布并进行灵敏度分析。
2. 隧道模型建立与参数选取
2.1. PDS技术
将ANSYS软件中的PDS模块应用到隧道结构的对状态函数进行函数分布、灵敏度、散点图等分析,在隧道工程中,常常具有复杂的力学关系以及不明确的地层结构环境,在大部分情况下基本变量之间的显式函数关系是不明确的。ANSYS使用的PDS技术与蒙特卡洛法原理相结合,分析结果直观、准确、实用性强。该技术采用大量的抽样模拟,模拟进程规避了极限状态方程的复杂性,收敛的速度不需要考虑基本变量的维数问题,同时PDS技术不需要考虑函数的推导问题和极限状态的曲面问题 [6]。故本文基于蒙特卡洛有限元方法,采用PDS技术为概率设计技术实现隧道二次衬砌的灵敏度分析。
2.2. 依托工程概况
本文中以实际工程项目为例,依托工程隧道隧址最高点地面标高约为1266.76米,对应的里程桩号为K19 + 658附近,整个隧道地表海拔高程介于1172.0~1266.8米,相对高差约为95.00米;该隧道地层岩性主要以中密碎石土和弱微风化石灰岩为主,形完整性较差,地貌形态变化较大。隧道最大埋深约为57.6 m,平均埋深32.5 m。隧道按高速公路单向双车道设计,设计速度为100 km/h。该隧道断面宽度11.8米,断面高度8.33米。隧道施工主要采用台阶法施工,初期支护后及时封闭,二次衬砌紧随开挖面,其中二次衬砌采用C25混凝土整体式浇筑,其设计厚度为45 cm。
2.3. 建立有限元模型
本文以该实际高速公路隧道工程作为研究背景,选取断面为该隧道的六心圆断面。模型采用“荷载–结构”法原理构建,通过ANSYS建立隧道的有限元分析模型,在程序中用二维梁单元(beam3)模拟衬砌,用弹性支撑(combin14)模拟弹性链杆即弹簧,建立弹簧可以代表衬砌与围岩之间的切向摩擦力和粘结力 [7],之后在等效节点对衬砌施加相关约束和荷载,通过计算结果表明,弹簧受拉的作用需要通过杀死相关受拉弹簧节点,以保证弹簧的受压状态,故在隧道拱顶区域存在抗力区,可不设置相关弹簧。结构模型如图1所示。
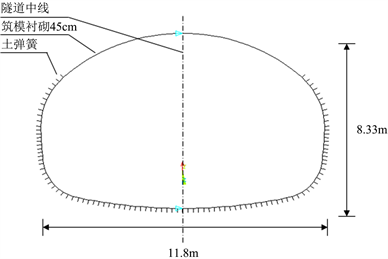
Figure 1. “Load-structure” model diagram
图1. “荷载–结构”模型图
2.4. 随机变量取值
随机变量作为影响隧道结构安全及稳定性的可能因素,本文将选取表1中的计算参数作为本次研究的随机变量,对参数的均值、标准差,及其分布进行定义,依据实际工程施工资料,并参考《公路工程结构可靠性设计统一标准》 [8] 以及《公路隧道设计规范》(JTG 3370.1-2018) [9] 相关规定,如表1所示。

Table 1. Summary table of features of random variables
表1. 各随机变量特征汇总表
3. 衬砌结构随机变量分布特征分析
采用蒙特卡罗方法中的超拉丁抽样方法,基于所构建的“荷载–结构”模型,输入二衬的随机输入参数值,对影响衬砌结构安全性的随机变量进行随机2000次抽样,计算并绘制二衬各个随机变量的分布曲线图,可以根据随机变量的数据离散性以及分布性状推断参数数据收敛、分布的合理性 [10]。通过对输入变量进行极限状态堆叠计算,得到本文计算中相关输入参数(包括衬砌厚度、衬砌弹性模量、围岩弹性反力系数、衬砌密度、垂直荷载及水平荷载)的分布函数图,图中横坐标为各随机变量取样数值,左纵坐标为概率密度值,右纵坐标为分布概率值,如图2~7所示。
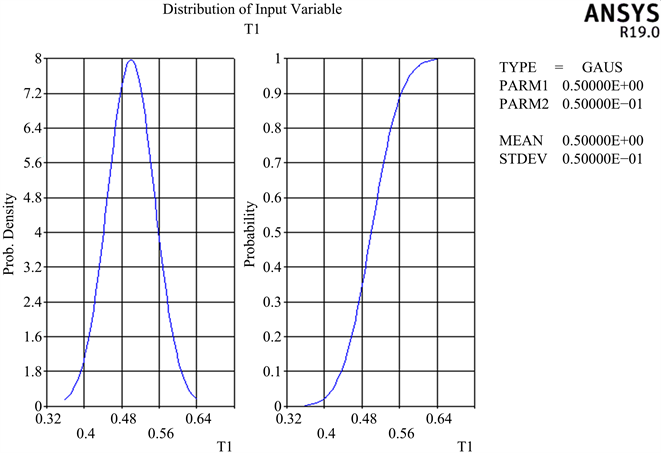
Figure 2. Lining thickness distribution curve
图2. 衬砌厚度分布曲线图
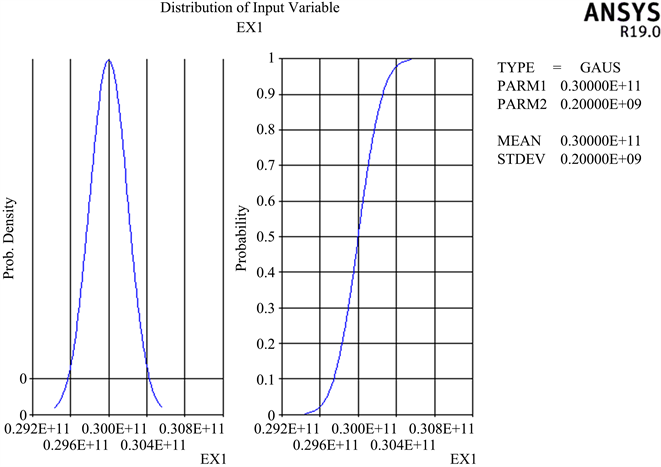
Figure 3. Lining elastic modulus distribution curve
图3. 衬砌弹性模量分布曲线图
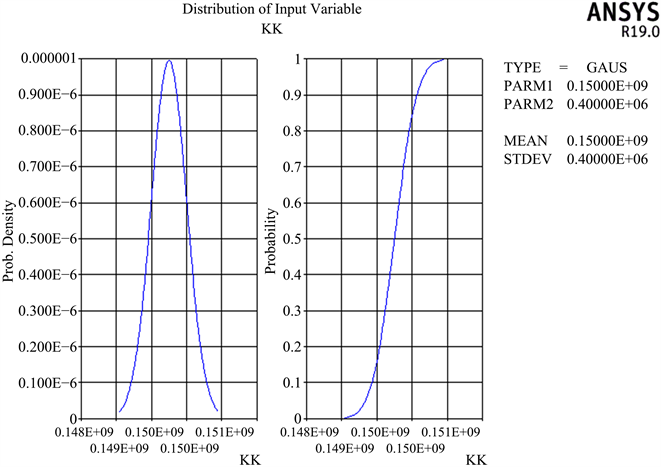
Figure 4. Lining elastic coefficient distribution curve
图4. 围岩弹性反力系数分布曲线图
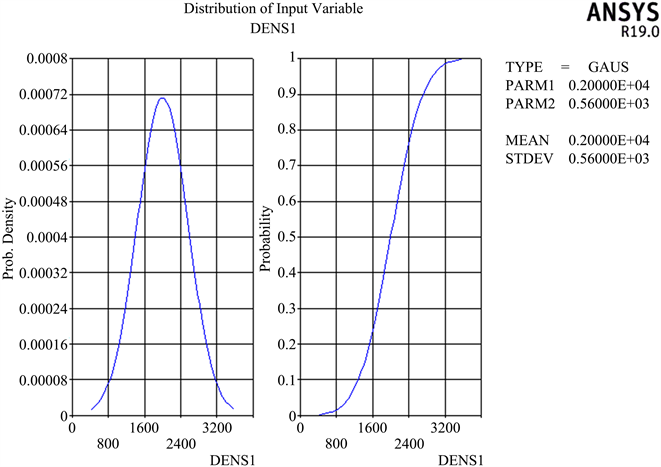
Figure 5. Lining density distribution curve
图5. 衬砌密度分布曲线图
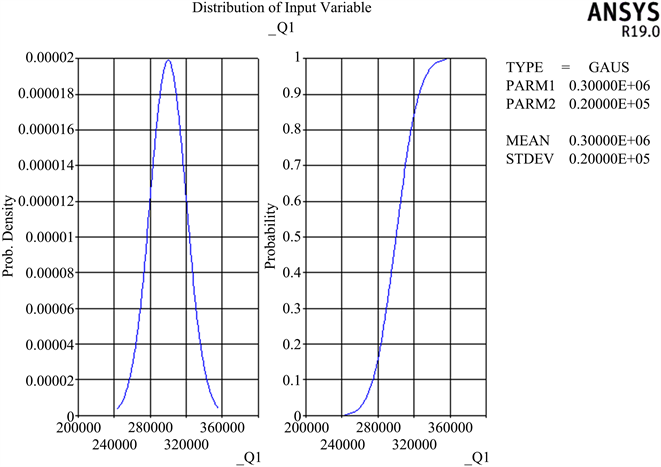
Figure 6. Vertical load distribution curve
图6. 垂直荷载分布曲线图
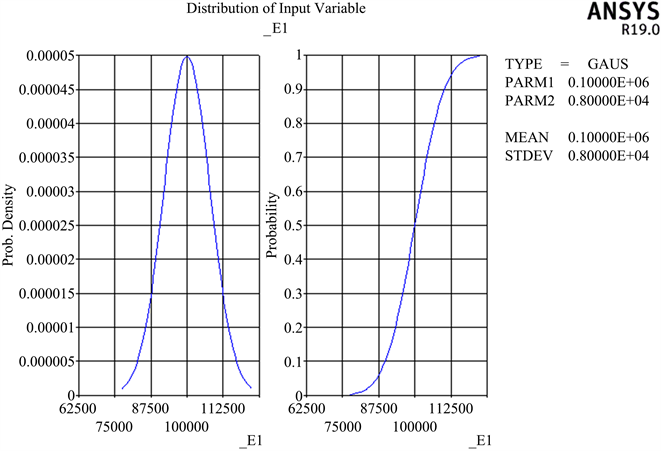
Figure 7. Curve of horizontal load distribution
图7. 水平荷载分布曲线图
由数据结果图2~7可得,衬砌结构的每一个随机变量的曲线图中曲线拟合均比较光滑,输入参数变量(衬砌的厚度、弹性模量、密度以及荷载和围岩弹性反力系数)分布符合设定分布曲线要求,并且曲线各区间都存在数据分布以及曲线连续并无中断,可以得出,数据统计结果收敛,也证明随机抽样样本数据充足,计算结果可靠,保证数据可以作为抽样累积数据以便于后续灵敏度分析。
4. 衬砌结构灵敏度分析
在整个灵敏度评价过程中至关重要的一点就是相关计算参数(二衬最大位移、最大剪力、最大轴力、最大弯矩)的灵敏度分析。通过灵敏度分析可以得到影响结构安全性的因素,及其重要程度。PDS技术通过量化表达形式(饼图)得出结果,随机变量的灵敏性会分为正负。灵敏度值为正时,随机输入变量越大,输出变量值就越大,当灵敏度数值为负时,随机输入变量越大,输出变量值就会越小 [11]。灵敏度分析可以通过对输入随机变量在输出变量分布规律中所占比影响大小,进而在大量参数变化下,分析各个影响因素的重要程度,针对每个研究对象,灵敏度分析给出了各随机变量对它的影响程度。本文选取隧道二次衬砌结构的最大位移,最大剪力,最大轴力,最大弯矩作为衬砌结构安全性的重要参数指标作为输出变量,并对其进行灵敏度分析,如图8~11所示。
从上述图8~11可得,二衬的最大位移的影响因素程度依次为衬砌厚度、水平荷载、衬砌密度、垂直荷载,其中最大影响因素衬砌厚度的影响占比为41%,二衬的最大剪力的因素程度依次为垂直荷载、衬砌密度、衬砌厚度、衬砌弹性模量,二衬的最大轴力的影响因素程度依次为衬砌厚度、水平荷载、垂直荷载,其中最大影响因素衬砌厚度影响占比为49%,最大弯矩的影响因素程度依次为衬砌厚度、水平荷载、垂直荷载、衬砌密度,其中影响最大影响因素衬砌厚度占比为43%,由此可得,隧道衬砌厚度是影响隧道二衬结构安全性的最重要的因素,是衬砌结构最大位移、最大轴力、最大弯矩的影响最大因素,影响占比均大于40%,在隧道施工中应当重点对隧道二衬结构厚度进行控制。
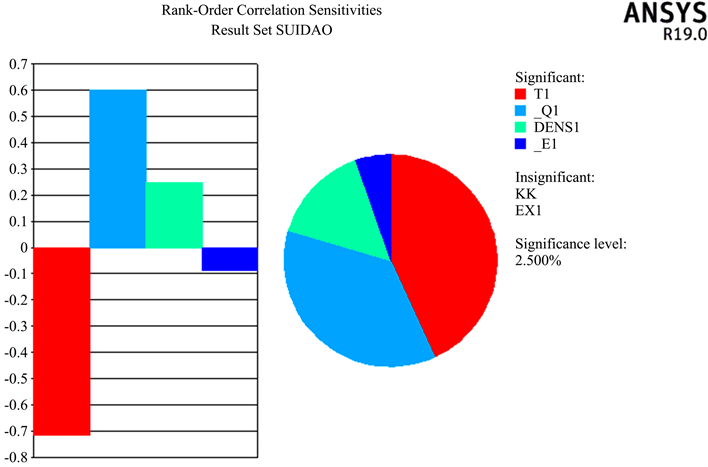
Figure 8. Maximum displacement sensitivity diagram
图8. 最大位移灵敏度图
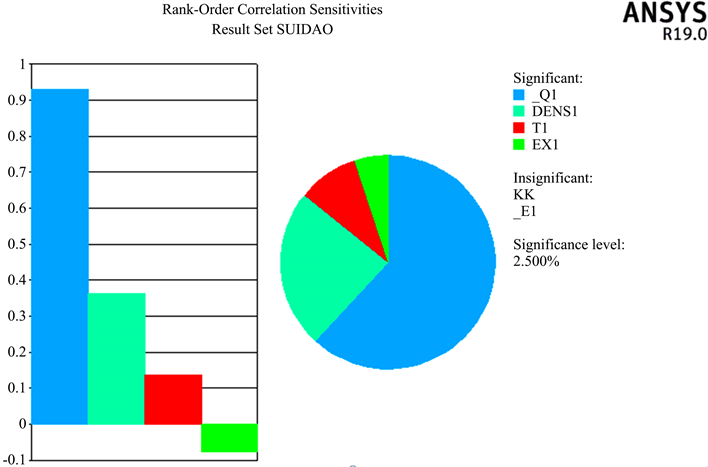
Figure 9. Maximum shear sensitivity diagram
图9. 最大剪力灵敏度图
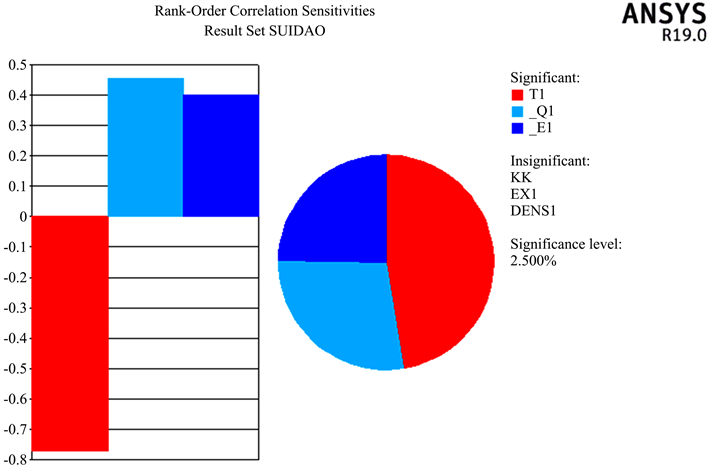
Figure 10. Maximum axial force sensitivity graph
图10. 最大轴力灵敏度图
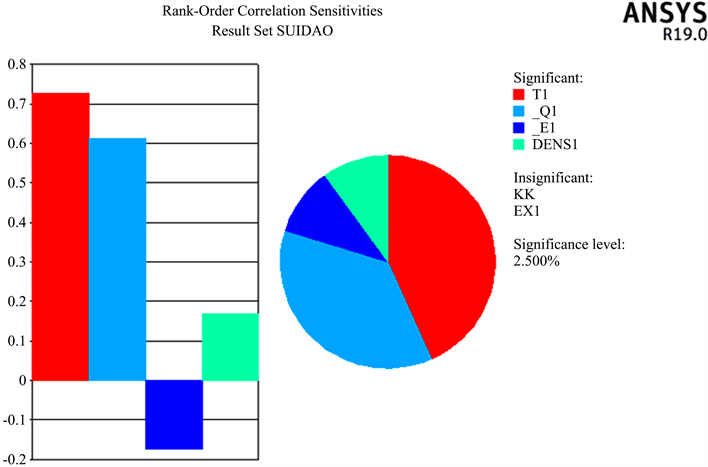
Figure 11. Maximum bending moment sensitivity diagram
图11. 最大弯矩灵敏度图
5. 衬砌结构输出变量关于厚度的线性相关性分析
散点图可以确定输入参数与输出参数的影响关系,即线性相关性大小 [12],探究线性相关性是探究随机变量影响规律的重要环节,通过线性相关性分析,可以得到输入变量与输出变量之间的线性关系,即数据离散点的走向趋势,以及通过密集程度和相关系数,来确定输入变量与输出变量的线性相关程度,并如何影响结构安全性变化规律 [13],通过PDS技术将输入参数与对应输出变量拟合,并绘制相关散点图,以探究统计数据相关规律性。通过灵敏度分析结果可知,衬砌厚度作为影响衬砌结构安全性影响程度最大变量,通过对二次衬砌厚度与其相关输出变量(二衬的最大位移、最大剪力、最大轴力以及最大弯矩)进行拟合计算,得到其变量散点图,以探析衬砌厚度的影响规律,趋势线斜率C1的大小代表输入参数对各输出参数的影响速率,相关系数r代表输入参数对输出参数的线性相关性程度,线性相关系数r代表输入参数对输出参数的线性相关性,线性相关系数r为正则代表参数为正相关,r数值为负代表参数负相关,r = 0为无关,|r| = 1表示完全线性相关,|r|越接近1表示线性相关性越大 [5],如图12~15所示。
由图12~15可得,衬砌厚度与衬砌输出变量(最大位移、最大剪力、最大轴力、最大弯矩)的散点图数据点集分布情况与趋势走向,其中衬砌厚度与最大位移、最大轴力和最大弯矩的离散型更加密集,线性分布更加明显,而衬砌厚度与最大剪力样本点较为离散,其中其趋势线斜率以及线性相关系数如表2所示。

Table 2. Table of lining thickness, trend line slope of random variables and linear orrelation coefficient
表2. 衬砌厚度与各随机变量趋势线斜率与线性相关系数表
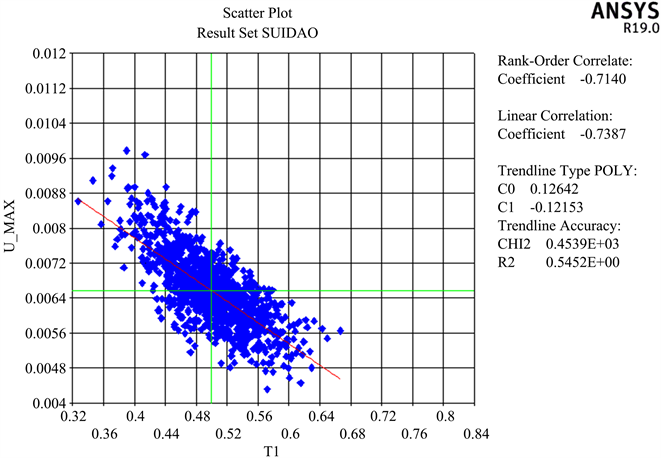
Figure 12. Scatter plot of lining thickness and maximum displacement
图12. 衬砌厚度与最大位移散点图
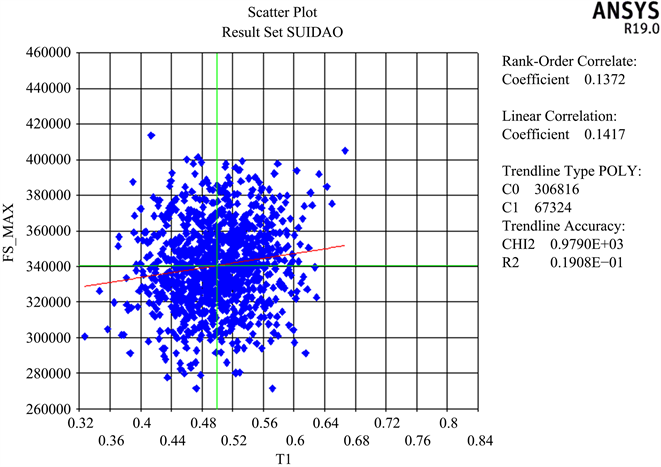
Figure 13. Scatter diagram of lining thickness and maximum shear force
图13. 衬砌厚度与最大剪力散点图
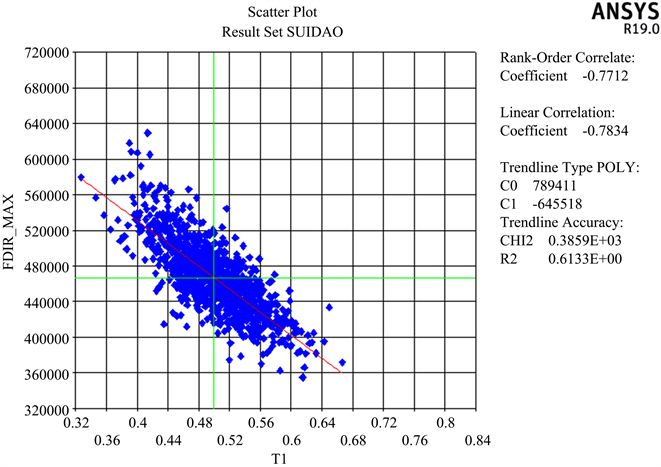
Figure 14. Scatter diagram of lining thickness and maximum axial force
图14. 衬砌厚度与最大轴力散点图
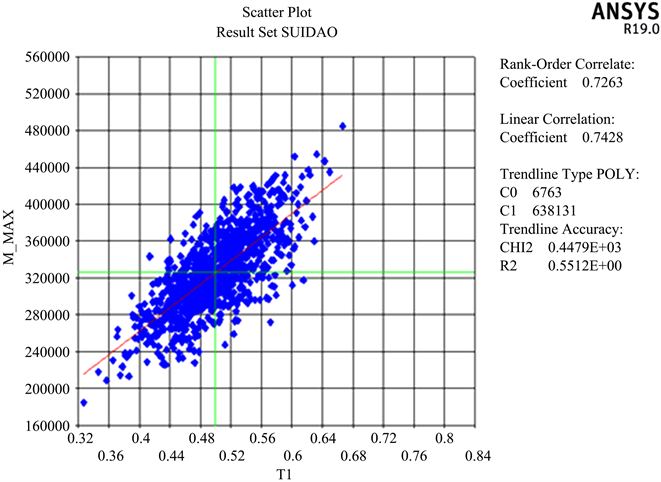
Figure 15. Scatter diagram of lining thickness and maximum bending moment
图15. 衬砌厚度与最大弯矩散点图
由表2可得,二衬厚度与最大位移、最大轴力、最大弯矩散点图的线性相关系数r数值均大于0.7,其线性相关程度明显,相关性较大,说明二衬厚度的变化对最大位移、最大轴力、最大弯矩的直接影响较为突出,其联系程度较为紧密。二衬厚度与最大剪力、最大轴力、最大弯矩的趋势线斜率C1数值较大,尤其二衬厚度与其最大压应力与最大弯矩的趋势线斜率均大于60,000,说明二衬厚度对最大剪力、最大轴力、最大弯矩的影响速率最大,当二衬厚度发生改变时,其最大轴力、最大剪力与最大弯矩的数值变化波动范围大,变化的速度较为明显。
6. 结论
1) 通过ANSYS计算程序,利用蒙特卡罗法对随机变量采取循环2000次分析,得到收敛数据,并对随机变量变量分布曲线图进行分析,验证抽样次数满足研究需求及其数据分布与数值的合理性,保证灵敏度分析结果的正确性。
2) 针对衬砌结构最大弯矩、最大位移以及最大剪力进行灵敏度数据分析,分析结构衬砌关于随机输入变量因素比例,得出影响隧道二次衬砌结构最大因素为衬砌厚度,其中衬砌厚度作为衬砌结构的最大位移、最大轴力、最大弯矩方面影响占比均大于40%,影响效果显著,在隧道施工过程中应当对其厚度重点控制。
3) 通过对衬砌结构散点图进行线性相关分析,得知衬砌厚度与相关输出变量指标线性相关程度大,影响速率大,二次衬砌厚度与二次衬砌结构的最大位移、最大轴力、最大弯矩得相关系数均大于0.73,线性相关性大,其中二衬厚度对最大剪力、最大轴力、最大弯矩的趋势线斜率数值较大,其影响速率较大,研究结果对隧道衬砌结构设计和施工提供经验参考。
基金项目
山西省回国留学人员科研资助项目(项目编号:2020-038)。