1. 引言
在当今,交通发展给我们生活带来了多方面的好处,因为它提高了人们的出行效率,也提高了社会的生产力。据统计 [1],截至2020年初,贵阳市民用车辆有168.71万辆,比上一年初增长了13.0%,其中汽车拥有量有134.12万辆,比上一年初增长了15.9%;私人汽车拥有量有119.70万辆,比上一年增长了16.5%。车辆数持续增长,会使交通问题愈加严重,对于交通拥堵带来的影响,如何有效减少和解决显得尤为重要,短时交通流预测是交管部门有效管理采取实施的主要依据。
2017年Nicholas G. Polson和Vadim O. Sokolov开发了一种深度学习模型来预测交通流量,显示出深度学习如何提供精确的短期交通流预测 [2]。2018年Unsok Ryu为了提高短期交通流量预测的性能,提出了互信息(MI)构造交通状态向量的方法,并且此方法在短期交通预测中具有良好的预测精度 [3]。2020年Azadeh Emami提出了一种基于褪色记忆卡尔曼滤波融合连接车辆和蓝牙传感器数据的短时交通流预测方法 [4]。国内对于交通流预测的研究也发展的十分迅速。胡伍生等人 [5] 为充分利用统计数据,提高交通流预测精度,在2020年构建了一种新颖的短期交通流预测的神经网络BP模型。温美玲 [6] 等针对交通拥堵问题,在2021年提出了基于轨迹大数据的交通拥堵评估和预测方法,使用深度学习算法建立了交通拥堵预测模型。孙越 [7] 等人在2021年提出一种ARMA-LSTM组合模型的对铁路客流量进行预测。温惠英 [8] 等人在2021年提出一种基于时延特性的短时交通流预测研究;张国赟 [9] 等人在2022年提出一种改进ARIMA模型对城市轨道交通短时客流进行预测。GPR是基于统计学习理论和贝叶斯理论发展起来的一种机器学习方法,适于处理非线性复杂回归问题,且泛化能力强,与神经网络、支持向量机相比,GPR容易实现,因此本文提出一种基于GPR模型与SARIMA模型相结合的方法来解决道路交通流预测问题,实验结果表明该组合模型的预测效果要优于其他单一预测模型。
2. 数据来源及研究方法
2.1. 数据来源
本文的数据是来自贵州省贵阳市观山湖区过车数据,它涉及到观山湖区的长岭南路与阳关大道等71个交叉路口的过车量,包括了2020年4月13日00:00到2020年4月17日19:10每五分钟的过车量,总共有1384个数据,使用15分钟作为间隔时间,最终分析的数据有461个。1小部分数据如下表1所示:

Table 1. Traffic flow section data
表1. 交通流部分数据表
根据表1可以看出最后的四个数据很明显为异常数据(一般是指出现不在范围的数据),倒数第五个数据也出现一定的偏差,而这里交通流数据的异常数据一般指交通流远小于道路通行能力,这里出现异常数据的原因可能有如下方面:一是设备出现故障,二是车流量密度过大造成收集数据不能正常传送到目标位置。异常数据会影响到后面数据分析预测的精度,因此需要对异常数据进行分析处理,使数据具有较高的质量,从而去提高交通流的预测精度。
对于异常数据的处理,在不考虑突发因素(比如交通事故)情况下,一般是先将其删掉再采用近似值修复补齐方式。这里使用相邻时段交通流量的平均值法,公式如下:
(1)
式中
是与t时刻相邻的交通流量期望值,
是与t时刻相邻的交通流量的标准差,取四个
时刻与t时刻相邻。由此计算得到最后五个数据修补后的值分别为38,985、37,904、35,555、32,607、30,609。
2.2. 研究方法
2.2.1. SARIMA模型
季节性差分自回归滑动平均 [10] (Seasonal Autoregressive Integrated Moving Average, SARIMA)模型是指序列中的季节效应和其他效应之间的关系具有一定的关系。又根据对季节效性提取的难易程度,将其分为简单季节模型与乘积季节模型。
a) 简单季节模型。当序列中的季节效应与其他效应之间的关系属于加法关系,即:
这个时候的各种效应的信息提取是较容易的,然后使用d阶的趋势差分,D步的季节差分运算,将简单的季节性模型拟合到原始序列的观测值。模型结构如下:
(2)
式中:
D为周期的步长,d是提取趋势信息所用的差分阶数,
为白噪声序列,并且
,
。
,为p阶自回归系数多项式。
,为q阶移动平均系数多项式。
该简单季节模型简记为
。
在使用SARIMA模型预测时,首先需要判断该序列的平稳性与季节性,如果序列为非平稳序列,则要通过差分的方式使之达到平稳序列,然后再用ARMA建模进行预测。
b) 乘积季节模型。当序列中的季节效应与其他效应之间的关系属于乘法关系,即:
这个时候使用d阶的趋势差分,D阶以S为周期的季节差分运算,将乘积的季节性模型拟合到原始序列的观测值。模型结构如下:
(3)
式中:
该乘积季节模型简记为
。
2.2.2. GPR模型
高斯过程回归 [11] (Gaussian Process Regression, GPR)模型,它可以是线性模型,也可以是非线性模型,本文利用它建立非线性回归模型,它是利用Bayes思想的一种监督学习方法,也是一种非参数回归。简单来说,就是通过贝叶斯的方法求出参数的后验分布,然后根据参数的后验分布与训练数据来求出测试数据的分布,从而进行贝叶斯估计与区间预测 [12]。它与支持向量机相较,模型比较好解释,并且它加入了噪声过程,能够更好拟合数据,抓取数据信息。该回归模型可表示为
(4)
其中
表示知道的回归函数,
是未知的回归系数向量,
是一个0均值的平稳高斯过程。
描述
的长期趋势,而
模型则是局部偏离长期趋势。
假设
表示知道的
个训练数据,
表示未知的
个测试数据,
和
分别表示训练数据与测试数据过程模
型。假设
(5)
其中
表示过程精度,
和
分别表示测试集与训练集的回归函数。
表示
的密度函数,则由贝叶斯公式可得到
后验分布的密度函数为
(6)
则由式(6)和多元正态分布的条件分布可得到
(7)
(8)
假设
的先验信息分布服从一个多元正态分布,也就是
,从而可以得
的后验分布为
(9)
从而得到测试数据
的预测分布为
(10)
得到预测数据
。对于训练数据与测试数据之间的协方差我们利用核函数进行求解,也就是
。
2.2.3. SARIMA-GPR模型
在实际应用中,由于交通流数据的复杂性与多变性,在做预测的时候可能会伴随着许多不确定的影响因素。并且对于交通流预测问题,可以采用不同的预测方法去建立多种模型进行预测,但是没有哪一个模型能够完全用于所有的交通状况,因此利用多个单一的模型来进行组合预测。组合模型能够有效的利用单一模型的优点,按照一定的规律将各种单一的模型组合起来。
在该组合模型当中,最重要的就是权值的选择,这是因为用不同的模型对同一个序列提取到的信息是不同的,因此,权值的选择会决定着模型预测的好坏。这里使用MAE权重系数 [13] 来构建组合模型,对于MAE小的模型所占的权重要大,从而提升预测效果。
观测数据为
,SARIMA与GPR的预测模型
在t时刻预测值记为
,设其权重为
,因此可以得到组合预测模型为
(11)
得到该组合模型的MAE为:
。
,
分别是这两个模型的MAE。
3. 实例分析
3.1. 基于SARIMA-GPR模型的道路车流量预测
把处理后的这461个数据按照8:2的比例划分为训练集与测试集。即是使用384个数据(2020年4月13日00:00到2020年4月16日23:45来训练模型,77个数据(2020年4月17日00:00到2020年4月17日19:00)来测试模型的好坏。通常评价一个模型最优的预测评价方法就是将预测误差尽可能降到最小。预测误差的计算方法有很多种 [14]:有常见的均方误差根(RMSE)、平均误差(ME)、平均绝对误差(MAE)、平均百分比误差(MPE)、平均绝对百分比误差(MAPE)等。
本文对模型的预测效果的好坏评估采取均方误差(RMSE)、平均绝对误差(MAE)以及平均绝对百分比误差(MAPE)。其计算公式分别为:
其中,
表示真实值,
表示预测值,n表示数据的个数。判断为:RMSE、MAE和MAPE的值越小,就证明预测的模型具有更好的精度。
对数据先进行SARIMA信息提取,观察数据的时序图以及自相关系数图进行建模。
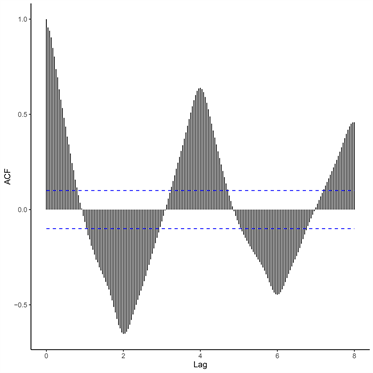
Figure 1. Traffic flow time series diagram (left) and autocorrelation coefficient diagram (right)
图1. 车流量时序图(左)与自相关系数图(右)
看出车流量数据伴随着一定的季节性(周期性),有着明显的非线性趋势,属于非平稳数据。季节波动的振幅不受到趋势变动的影响,那么季节与趋势之间通常没有交互影响关系,因此采用简单季节模型。根据图1 (右),以及R中auto.arima函数自动定阶,根据模型定阶原则,再根据AIC与BIC准则 [15],建立了
模型。
得到该模型残差检验结果如下表2所示。当延迟期数为6期的时候,模型假设检验的p值为0.1187显著大于0.05,即是认为在0.05的显著性水平下不能拒绝原假设,因此,该残差序列为白噪声序列,即表明残差序列中相关信息已经被提取出来了,所以所建立的模型有效。

Table 2. Model residual series test results
表2. 模型残差序列检验结果
对于高斯过程回归模型,令
,核函数使用最常见的高斯径向基核函数与能对周期性建模的正弦平方内核函数进行组合使预测效果更好。高斯径向基核函数和正弦平方内核函数公式分别为
(12)
则可以使用组合的核函数
(13)
其中
表示长度的缩放系数,p表示核函数的周期。对于模型参数的求解,利用对数边际似然方法,进行求解,见(6)式。通过计算得到参数
。
基于以上分析,可以知道SARIMA模型的平均绝对误差(MAE)
,GPR模型的平均绝对误差(MAE)
,可以得到组合模型的权重值分别为
。
3.2. 模型预测对比图

Figure 2. Comparison of predicted values and true values of three single models
图2. 三种模型预测值与真实值对比图
从图2可以看出SARIMA模型(左)、GPR模型(中)和SARIMA-GPR模型(右)在整体上的拟合效果还是不错的,预测值与真实值大致走势一样,但明显看出SARIMA-GPR模型预测值更接近真实值,表明所提出的模型更有效。
3.3. 模型预测效果对比分析
为了进一步说明SARIMA-GPR模型对该道路交通流数据的预测效果,采用相同的数据训练方式对SVM模型进行训练,SVM也是对数据进行非线性拟合较好的一个模型,以及用同样的权值选择方式构建一个SARIMA-SVM模型并对其进行训练,对它们进行预测效果评估(表3,图3)。

Table 3. Comparison of the prediction effects of the five models
表3. 五种模型的预测效果对比结果

Figure 3. Comparison diagram of absolute error prediction of five models
图3. 五种模型预测绝对误差对比图
通过表3看出SARIMA-GPR模型预测结果的MAE与MAPE是这五种模型里面是最小的,SARIMA- GPR模型预测平均绝对误差(图3)要小于其他几个模型,预测效果也要优于其他模型。SARIMA模型能够很好拟合数据线性部分,GPR模型考虑到数据的噪声,能够更好抓取数据信息,将两者结合,对原序列的预测效果更好,因此说SARIMA-GPR模型测效果是最好的,能够很好提高预测准确度。
4. 结论
通过对贵阳市观山湖区的交通流数据进行分析,可以知道该交通流数据属于非平稳的时间序列数据,具有一定的季节特征,也有非线性特征。针对于交流流量的特征,提出了一种基于机器学习的SARIMA- GPR模型对该道路交通流进行预测。实验结果表明,该模型综合了单一模型的优势,使预测效果更好,提高了预测精度。本文的数据是五天工作日的数据,在以后可以考虑获取非工作日的数据再次进行建模,使预测效果达到最好。
基金项目
国家自然科学基金资助项目“道路交通数据的统计模型诊断理论与应用研究”(12161016)。