双盘转子碰摩故障动力学特性分析

Analysis of Dynamic Characteristics of Rub-Impact Fault of Double-Disk Rotor

摘要: 针对两端刚性支承的动力涡轮双盘转子，使用符合库伦摩擦定律的局部碰摩力模型来定义其径向摩擦力与切向摩擦力。利用Timoshenko梁单元对其进行动力学建模，推导出单元的刚度矩阵和质量矩阵，并将各个单元矩阵组装成系统的总矩阵，写出整个系统的微分方程。采用Newmark-β方法对双盘碰摩故障转子系统进行解析，分别揭示了两个盘的碰摩间隙、接触刚度、摩擦系数对系统动力学特性响应的规律。分析结果表明：该系统呈现出多周期、拟周期和混沌等丰富的非线性动力学特性；碰摩引起振动主要为其自振频率成分，同时伴有其它较小的分数倍频振动及两侧相加为2倍频的分频。

Abstract: For a power turbine double-disk rotor with rigid supports at both ends, the radial friction force and tangential friction force are defined by a local friction force model in accordance with Coulomb’s law of friction. The stiffness matrix and mass matrix of the element are derived by using Timoshenko beam element for dynamic modeling, and each element matrix is assembled into the total matrix of the system, and the differential equation of the whole system is written. The Newmark-β method was used to analyze the rotor system with rub-impact fault of two disks, and the response laws of rub-impact clearance, contact stiffness and friction coefficient of two disks to the system dynamic characteristics were revealed respectively. The analysis results show that the system presents rich nonlinear dynamics characteristics such as multi-period, quasi-period and chaos. The vibration caused by rubbing is mainly the natural frequency component, accompanied by other smaller fractional frequency doubling vibration and the frequency division which adds up to 2 times frequency on both sides.

1. 引言

现代涡轴发动机的发展追求更高的推重比和较低的能耗，叶片和机匣之间预留的间隙越来越小，使得涡轴发动机中涡轮转子与机匣发生碰摩故障的概率增大。尽管对于转子碰摩问题的相关研究已经很多，但是对于动力涡轮转子双盘碰摩故障研究相对较少。

针对简单的Jeffcott转子模型，国内外较多学者均采用集中质量法进行建模，讨论由碰摩导致的复杂非线性动力学特性。随着转子动力学及计算机软硬件的发展，越来越多的学者采用有限元建模 [1] [2] [3] [4] [5]，其足够的建模精度以及较宽的频率分析范围使得有限元建模方法逐渐成为主流。对于双盘转子系统的非线性动力特性研究，刘洋等 [6] 建立了双盘转子轴承系统有限元模型，研究电机联轴器不对中情况下系统碰摩故障动力学特性，以及支座松动情况下发生碰摩故障振动响应特性。袁惠群等 [7] 考虑了机轴弹性和陀螺效应建立了双盘碰摩转子动力学模型，研究了双盘碰摩下系统非线性动力学特性。徐可君等 [8] [9] 建立一个新型径向–轴向复合碰摩双盘转子系统力学模型，以此模型进行数值分析，结果表明系统具有强非线性运动，拟周期和混沌是系统碰摩的主要特征。耿康康 [10] 针对双盘转子模型，研究了不同数量圆盘发生碰摩故障时系统响应的特征，发现双盘转子系统在低转速、临界转速以及较高转速下的响应分别以周期、拟周期和混沌为主。

转子系统碰摩故障是一种强非线性运动，在建立相关模型后，各学者通常采用以直接积分法为基础的解析方法对振动响应进行求解，常用于解析非线性系统运动方程的方法有Runge-Kutte法、Newmark-β法、Wilson-θ法等。其中Newmark-β法解析的结果与步长大小无关，算法稳定，因此采用Newmark-β法来解析双盘碰摩故障转子系统动态响应。

2. 双盘转子系统碰摩故障有限元模型

双盘动力涡轮转子系统模型采用考虑剪切变形的Timoshenko梁单元进行建模，图1为梁单元示意图。将转轴划分若干个单元，其中每个单元包含二个节点，每个节点具有五个自由度，分别为x、y方向的平移自由度和绕x、y及z轴的转动自由度。

Figure 1. Timoshenk beam element

图1. Timoshenko梁单元

图1中坐标系是Oxyz，x₁、y₁分别为梁单元第一个节点x、y方向的位移，x₂、y₂分别梁单元第二个节点x、y方向的位移，θ_xA、θ_yA、θ_zA分别为第一个节点的x、y、z方向转角，θ_xB、θ_yB、θ_zB分别为第一个节点的x、y、z方向的转角，转子系统的Timoshenko梁模型的自由度为：

$q_e={\left[x_A{y}_A{\theta }_{xA}{\theta }_{yA}{\theta }_{zA}{x}_B{y}_B{\theta }_{xB}{\theta }_{yB}{\theta }_{zB}\right]}^{\text{T}}$ (1)

2.1. 转子系统有限元建模

由广义有限元的运动方程，可以得到在固定坐标系下的运动方程为：

$\left[M\right]\left\{\ddot{q}\right\}+\left[C\right]\left\{\stackrel{\dot{}}{q}\right\}+\left[K\right]\left\{q\right\}=\left\{P\right\}$ (2)

式中，[M]为系统整体质量矩阵；[C]为系统整体阻尼矩阵；[K]为系统整体刚度矩阵；{q}为位移向量；{P}为圆盘所受碰摩力，陀螺效应对本系统影响较小，因此忽略陀螺效应。其中K_e和M_e分别为是轴段单元刚度矩阵和单元质量矩阵，具体形式是一个十阶对称矩阵：

$K_e=\left[\begin{array}{cccccccccc}{k}_1& & & & & & & & & \\ 0& k_1& & & & & & & & \\ 0& -k_2& k_3& & & & & & & \\ k_2& 0& 0& k_3& & & & & & \\ 0& 0& 0& 0& k_5& & & & & \\ -k_1& 0& 0& -k_2& 0& k_1& & & & \\ 0& -k_1& k_2& 0& 0& 0& k_1& & & \\ 0& -k_2& k_4& 0& 0& 0& k_2& k_3& & \\ k_2& 0& 0& k_4& 0& -k_2& 0& 0& k_3& \\ 0& 0& 0& 0& -k_5& 0& 0& 0& 0& k_5\end{array}\right]$ (3)

$\begin{array}{l}{M}_e=\frac{\rho \pi L\left(r_o^2-r_i^2\right)}{840{\left(1+\Phi \right)}^2}\left[\begin{array}{cccccccccc}312& & & & & & & & & \\ 0& 312& & & & & & & & \\ 0& -44L& 8L^2& & & & & & & \\ 44L& 0& 0& 8L^2& & & & & & \\ 0& 0& 0& 0& 0& & & & & \\ 108& 0& 0& 26L& 0& 312& & & & \\ 0& 108& -26L& 0& 0& 0& 312& & & \\ 0& 26L& -6L^2& 0& 0& 0& 44L& 8L^2& & \\ -26L& 0& 0& -6L^2& 0& -44L& 0& 0& 8L^2& \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\\ +\frac{\rho \pi \left(r_o^4-r_i^4\right)}{120L}\left[\begin{array}{cccccccccc}36& & & & & & & & & \\ 0& 36& & & & & & & & \\ 0& -3L& 4L^2& & & & & & & \\ 3L& 0& 0& 4L^2& & & & & & \\ 0& 0& 0& 0& 0& & & & & \\ -36& 0& 0& -3L& 0& 36& & & & \\ 0& -36& 3L& 0& 0& 0& 36& & & \\ 0& -3L& -L2& 0& 0& 0& 3L& 4L^2& & \\ 3L& 0& 0& -L2& 0& -3L& 0& 0& 4L^2& \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\end{array}$ (4)

其中：

$\begin{array}{l}{k}_1=\frac{12E{I}_e}{L^3\left(1+\Phi \right)},k_2=\frac{6E{I}_e}{L^2\left(1+\Phi \right)},k_3=\frac{\left(4+\Phi \right)E{I}_e}{L\left(1+\Phi \right)}\\ k_4=\frac{\left(2-\Phi \right)E{I}_e}{L\left(1+\Phi \right)},k_5=\frac{G_e{I}_p{L}^2\left(1+\Phi \right)}{E{I}_e}\end{array}$ (5)

公式中 $\Phi =12E{I}_e/\kappa G_{e}A{L}^2$，E是轴段材料弹性模量，I_e是截面惯性距，G_e是轴段剪切模量，L是轴段长度，r_o，r_i分别为空心轴段的外径与内径，由于是转子系统是空心轴段，因此梁单元剪切影响因子 $\kappa =2\left(1+\mu \right)/\left(4+3\mu \right)$，μ是材料泊松比。

建立刚性圆盘，M_w和C_w分别为圆盘单元质量矩阵和圆盘单元阻尼矩阵。

$M_w=\left[\begin{array}{ccccc}{m}_w& 0& 0& 0& 0\\ 0& m_w& 0& 0& 0\\ 0& 0& J_d& 0& 0\\ 0& 0& 0& J_d& 0\\ 0& 0& 0& 0& J_p\end{array}\right],C_w=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& J_p& 0\\ 0& 0& -J_p& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]$ (6)

其中J_d和J_p分别为圆盘直径转动惯量和圆盘极转动惯量，m_w为圆盘质量。

将空心轴段梁单元和刚性圆盘各个单位矩阵如图2方式进行组装，左侧为各节点单位矩阵，右侧为系统总矩阵，黑色部分为两个相邻节点矩阵叠加部分。至此动力涡轮转子系统有限元模型建立全部完成。

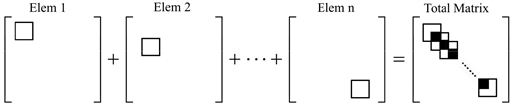
Figure 2. Schematic diagram of matrix assembly mode

图2. 矩阵组装方式示意图

Figure 3. Finite element model of double disk power turbine rotor

图3. 双盘动力涡轮转子有限元模型

根据上述建模过程，建立一个双盘动力涡轮转子有限元实体模型如图3，此模型由16个节点，15个梁单元组成，左盘1加载在节点4上直径为0.3 m，右盘2加载在节点5直径为0.2 m，支承和阻尼单元分别加载在节点2和节点14上。圆盘和轴段所用材料相同，并给出动力涡轮转子系统模型参数如表1。

Table 1. Parameters of double disk power turbine rotor system

表1. 双盘动力涡轮转子系统参数

2.2. 碰摩力模型

Figure 4. Schematic diagram of rub-impact force

图4. 碰摩力示意图

转子与静子之间的周向局部碰摩示意图如图4所示，图中P_N为径向碰摩力，P_T为切向摩擦力，φ为碰摩点的法向与z轴的夹角，ω为转子转动角速度，e为转子轴心位移。假设静子径向变形为线性变形，k_r为静子径向刚度，转子与静子间的摩擦符合库伦摩擦定律，摩擦系数为f，即摩擦力跟作用在摩擦面上的正压力成正比，并设静止时转子与静子之间的间隙为δ₀，则该碰摩力为：

$\{\begin{array}{l}{P}_N=\left(e-{\delta }_0\right)\\ P_T=f\cdot P_N\end{array}e\ge {\delta }_0$ (7)

式中， $e=\sqrt{y^2+z^2}\ge {\delta }_0$ 为转子径向位移。将碰摩力分解到y-z坐标系中，有：

$\left\{\frac{P_y}{P_z}\right\}=-\frac{\left(e-{\delta }_0\right)k_r}{e}\left[\begin{array}{cc}1& -f\\ f& 1\end{array}\right]\left\{\frac{y}{z}\right\}e\ge {\delta }_0$ (8)

3. 仿真结果与分析

对于非线性转子系统振动响应求解，各学者通常采用以直接积分法为基础的解析方法，常用于解析非线性系统运动方程的方法有Runge-Kutte法、Newmark-β法、Wilson-θ法等。其中Newmark-β法解析的结果与步长大小无关，算法稳定，因此采用Newmark法来解析动力涡轮转子系统动态响应。

3.1. 转/静间隙对转子系统的影响

转静子的间隙是影响转静子碰摩程度的重要参数，故本小节以间隙为变量，研究不同转静子间隙下转子系统碰摩故障振动响应的变化。为了针对转静间隙单一因素对转子振动响应的影响进行分析，分别取圆盘1与圆盘2作为碰摩对象，将工作转速设定为3000 r/min，偏心量分别设定为3 × 10⁻⁴ kg∙m、4 × 10⁻⁴ kg∙m，碰摩刚度均为6 × 10⁸ N/m，摩擦系数均为0.1，对转子的时域振动响应进行分析，同时对时域信号进行傅里叶变换，以求得其频谱特征。图5~10是盘1与盘2分别在间隙为3 × 10⁻⁴ m、5 × 10⁻⁴ m、9 × 10⁻⁴ m发生碰摩故障情况下的轴心轨迹图、频谱图和Poincare截面图。

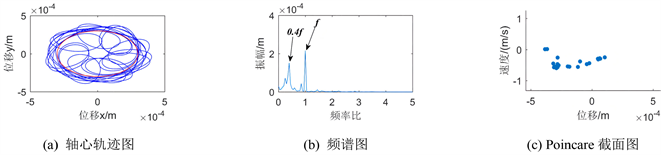
Figure 5. Vibration response diagram of the system when the clearance of disc 1 is 3 × 10⁻⁴ m

图5. 盘1间隙为3 × 10⁻⁴ m时系统振动响应图

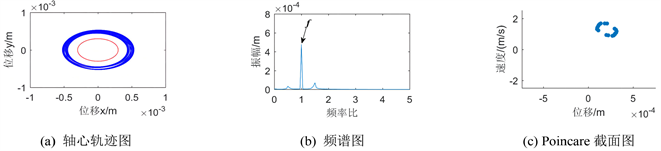
Figure 6. Vibration response diagram of the system when the clearance of disc 2 is 3 × 10⁻⁴ m

图6. 盘2间隙为3 × 10⁻⁴ m时的系统振动响应图

图5、图7、图9绘制了盘1在间隙不断增大过程中发生的碰摩故障情况下的三种图。从图5看转静子间隙为3 × 10⁻⁴ m时盘1的轴心轨迹图较为复杂，可知发生了较为强烈的振动，随着间隙增大到5 × 10⁻⁴ m时，其轴心轨迹图是较为均匀的椭圆轨迹，间隙再增大到9 × 10⁻⁴ m时可以看到轨迹比较稀疏，随着转静间隙增大，各个轴心轨迹图的幅值减小，可知碰摩故障现象逐渐减弱。从频谱图上看随着间隙增大，系统表现出不平衡故障导致0.4倍频、0.35倍频、0.3倍频等，因此，可以通过故障转子系统的振动信号，分析其频率组分来对转子故障进行有效的诊断。

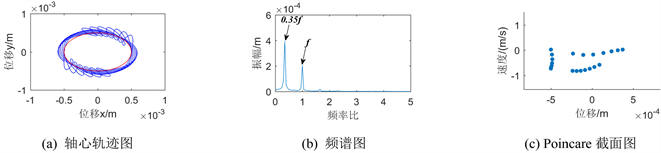
Figure 7. Vibration response diagram of the system when the clearance of disc 1 is 5 × 10⁻⁴ m

图7. 盘1间隙为5 × 10⁻⁴ m时的系统振动响应图

Figure 8. Vibration response diagram of the system when the clearance of disc 2 is 5 × 10⁻⁴ m

图8. 盘2间隙为5 × 10⁻⁴ m时的系统振动响应图

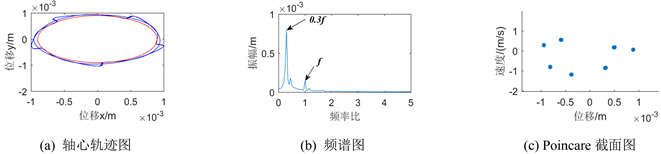
Figure 9. Vibration response diagram of the system when the clearance of disc 1 is 9 × 10⁻⁴ m

图9. 盘1间隙为9 × 10⁻⁴ m时的系统振动响应图

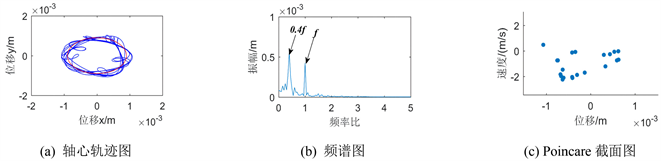
Figure 10. Vibration response diagram of the system when the clearance of disc 2 is 9 × 10⁻⁴ m

图10. 盘2间隙为9 × 10⁻⁴ m时系统振动响应图

图6、图8、图10绘制了盘2在间隙不断增大过程中发生的碰摩故障情况下的三种图。在间隙为3 × 10⁻⁴ m、5 × 10⁻⁴ m时盘2的轴心轨迹图较为均匀且超越边界，由此可知系统发生的碰摩故障较为明显，当接触间隙增大当9 × 10⁻⁴ m时，其轴心轨迹图变的较为混乱且有部分轨迹在间隙内，可知其碰摩现象减弱。从其频谱图上看，基本存在1倍频，以及1倍频两侧的分频组合相加为2倍频的现象。

Figure 11. Bifurcation diagram of system with speed under different clearances of disc 1

图11. 盘1不同间隙下系统随转速变化分岔图

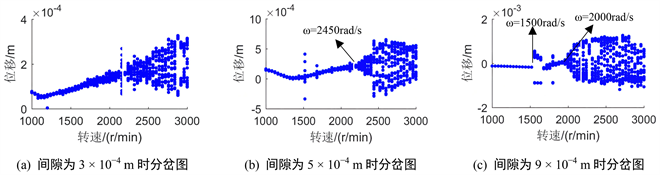
Figure 12. Bifurcation diagram of system with speed under different clearances of disc 2

图12. 盘2不同间隙下系统随转速变化分岔图

图11、图12分别是盘1和盘2不同间隙下系统随转速变化分岔图。图11(a)可以看出当系统工作转速小于1600 r/min时，系统处于较为混沌的状态，当转速处于1600 r/min~2750 r/min时，系统处于较为稳定的周期1运动，当转速大于2750 r/min时系统又处于混沌状态，结合图5(c)庞加莱截面图存在聚集的点和不规律分布的点可以验证转子系统从混沌状态到周期1运动再到混沌状态这一过程。图11(b)可以看出当转速小于1350 r/min时系统处于拟周期运动，当转速区间在1550 r/min~1750 r/min中时出现二倍周期分岔，当转速继续增大，系统处于混沌状态。图11(c)可以看出当转速小于2500 r/min时候分叉图为一直线，系统处于周期1运动，转速增大系统发生混沌。

图12反应了盘2在间隙增大过程中系统随转速变化当分岔图，图12(a)随着转速增大，分岔图位移也逐渐增大，可知系统不稳定性愈发增强。图12(b)在转速为1500 r/min时系统分岔图出现短暂拟周期运动，随后进入周期1运动，当转速大于2450 r/min时系统处于混沌状态。图12(c)当转速在1500 r/min出现短暂二倍分岔，后又进入周期运动，当转速大于2000 r/min系统处于混沌状态。

3.2. 接触刚度对转子系统的影响

以接触刚度为变量，讨论系统工作转速为3000 r/min时，接触刚度对转子系统的影响。系统参数：偏心量3 × 10⁻⁴ kg∙m、4 × 10⁻⁴ kg∙m，碰摩间隙6 × 10⁻⁴ m，摩擦系数均为0.1。对转子的时域振动响应进行分析，同时对时域信号进行傅里叶变换，以求得其频谱特征。

图13、图14分别绘制了不同接触刚度情况下盘1与盘2的轴心轨迹图与频谱图。图13显示随着接触刚度增加其轴心轨迹图变化不太大，频谱图皆存在1倍频和0.3倍工频。图14显示随着接触刚度增大可以看出：1) 盘2的轴心轨迹图幅值减小，但总体呈现为较均匀的轨迹图，处于拟周期运动；2) 从频谱图上看皆存在1倍频与两侧相加为2倍频的分频，且随着接触刚度增大，1倍频幅值减小较为明显。

3.3. 摩擦系数对转子系统的影响

以摩擦系数为参变量，讨论转速为3000 r/min时，摩擦系数对转子系统振动响应的影响。系统参数：偏心量3 × 10⁻⁴ kg∙m、3 × 10⁻⁴ kg∙m，碰摩间隙5 × 10⁻⁴ m，接触刚度均为6 × 10⁸ N/m。对转子的时域振动响应进行分析，同时对时域信号进行傅里叶变换，以求得其频谱特征。

图15绘制了不同摩擦系数下盘1发生碰摩故障时系统的轴心轨迹图与频谱图。随着摩擦系数的增大，轴心轨迹图愈发区域混乱状态，转子失稳的可能性在增加。分析转子系统在各个摩擦系数下频谱图可以看出：1) 转子转子双盘碰摩故障的频谱在不同摩擦系数下，均以基频为主，同时均出现0.35倍工频的分频成分；2) 三组摩擦系数频谱图显示当摩擦系数不断增大时，其振动幅值先增大后减小，在f = 0.25时其0.35倍工频幅值最大。而其1倍频幅值变化不大。

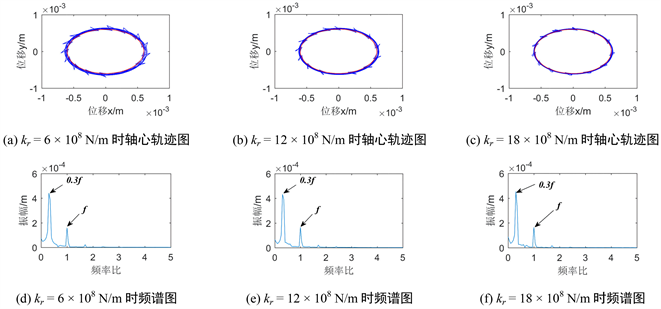
Figure 13. Vibration response diagram of system with different contact stiffness of disc 1

图13. 盘1不同接触刚度时系统振动响应图

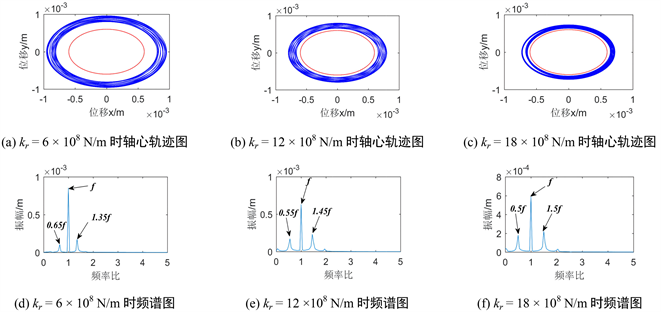
Figure 14. Vibration response diagram of system with different contact stiffness of disc 2

图14. 盘2不同接触刚度时系统振动响应图

图16绘制了盘2不同摩擦系数下发生碰摩故障时系统的轴心轨迹图与频谱图。与盘1不同的是盘2的轴心轨迹图随着摩擦系数的增大其轨迹变化不明显，始终处于拟周期运动中。分析转子系统在各个摩擦系数下频谱图可以看出：1) 三组图中均存在幅值较小的1倍频，且图16(d)与图16(f)均只存在一个分频；2) f = 0.25时，频谱图具有丰富的频率成分，除了存在1倍频以外，还存在0.2倍工频、0.4倍工频、0.6倍工频等，其0.4倍工频幅值相比于f = 0.15和f = 0.3要更大。

4. 总结

本文建立了双盘碰摩故障动力涡轮转子系统，运用数值积分方法，研究了转静子间隙、接触刚度、摩擦系数和不同碰摩位置对系统非线性动力学特性的影响规律。主要结论如下：

1) 转静间隙逐渐增大时，盘1频谱图工频左侧的分频呈现0.05倍频的递减，盘2存在工频且两侧均有分频。从分岔图上看盘2间隙增大，拟周期运动会向朝着低转速移动。

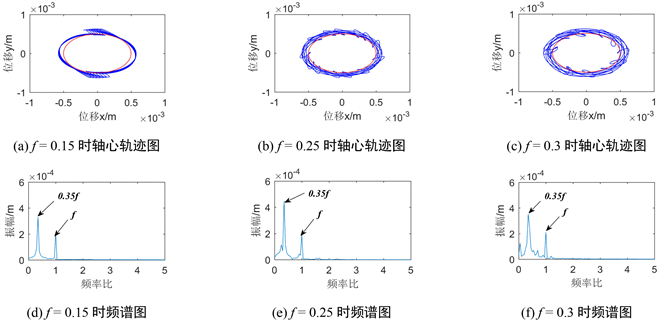
Figure 15. Vibration response diagram of system with different friction coefficient of disc 1

图15. 盘1不同摩擦系数时系统振动响应图

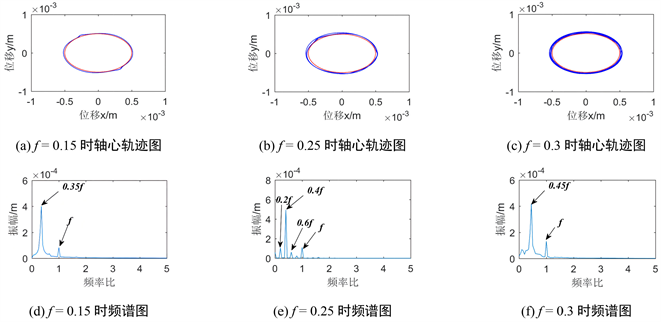
Figure 16. Vibration response diagram of system with different friction coefficient of disc 2

图16. 盘2不同摩擦系数时系统振动响应图

2) 随着接触刚度的不断增大，盘1碰摩程度几乎不变，其频谱图皆存在1倍频和0.3倍工频。盘2的轴心轨迹图幅值减小，总体呈现为较均匀的轨迹图，从频谱图上看皆存在1倍频与两侧相加为2倍频的分频，且随着接触刚度增大，1倍频幅值减小较为明显。

3) 摩擦系数增大时，转子系统振动幅值变化很小，轴心轨迹图较为稳定。盘1的频谱图均存在1倍频和0.35倍工频；当盘2的f = 0.25时频谱图存在0.2倍工频、0.4倍工频、0.6倍工频等丰富的频率成分。

NOTES

^*通讯作者。