1. 引言
2019年,新冠疫情的突然爆发对全球经济造成了巨大冲击,碳交易市场产生了剧烈的震荡。在全球疫情爆发之初,碳交易市场严重受挫 [1]。欧盟碳排放交易市场作为国际上发展最为成熟的碳交易市场之一,其碳排放权期权价格在2020年3月中旬低至15欧元,虽然在以欧盟为代表的国家推出的绿色发展疫情复苏计划的刺激下 [2] [3] [4],碳排放权期权价格有所回升,但此前造成的影响也不容忽视。因此,研究碳排放权期权定价机制及演化规律十分必要。
碳排放权期权是一种实物期权,实物期权是在金融期权的基础上发展而来的,与金融期权有一定的相似之处。因此,现有的碳排放权期权定价大多是借用金融期权定价方法 [5] [6] [7]。Black-Scholes (B-S)期权定价模型最先被应用于碳排放权期权研究中 [8],然而此模型是在众多假设条件下导出的,不能很好地反应真实市场现状 [9] - [14]。之后,众多学者对该公式做出了许多改进,例如针对资产价格的长期记忆性和波动率的随机性,提出了分形布朗运动期权定价法 [15] [16],并与GARCH [17] 模型结合,以此在碳排放权期权定价方面取得了良好的进展 [18] [19]。为了应对突发事件的影响,刘悦等 [20] 提出了机制转换的期权定价模型。但以上这些模型仍存在不足之处,如长期预测不稳定、突发事件导致价格发生剧烈波动时预测不准确等问题。
已有研究表明 [21],碳排放权期权的实物属性与金融期权也存在着不同之处,如收益的不确定性,碳排放权期权未来收益容易受到政策、经济发展以及投资者心理等因素的影响;不可交易性,碳排放权期权的标的资产可在市场上进行交易,其本身不可交易;投资的不可逆性,碳排放权期权投资者一旦投资,不可随意撤资;先后关联性,碳排放权期权的价值不仅仅取决于自身特征,还与市场上其他期权存在着十分密切的联系。因此,碳排放权期权的定价法应充分考虑收益的不确定性、投资的不可逆性以及先后关联性,以期提升决策者评估的有效性和客观性。但已有的碳排放权期权定价模型并未将其充分考虑在内,存在一定的不足,因此,为了能够为投资者和决策者提供更为合理的投资策略,需要建立一个适用于实物期权特性的定价模型。李响楚涵 [22] 针对实物期权特有的性质,将RBF神经网络模型应用于实物期权定价中,得到的RBF神经网络模型预测准确性远远高于B-S期权定价模型,稳定性相对较好,没有预测误差过高的情况出现,为实物期权定价模型提供了新的思路。由于本文主要讨论新冠疫情下实物期权定价问题,因此寻找能够快速捕捉到新冠肺炎对碳排放权期权数据影响的定价模型显得尤为重要。针对突发事件对碳排放权期权数据的影响,Li等 [23] 提出了机制转换的跳–扩散模型,与BSM和JDM相比,RSJM在碳排放市场上具有较高的解释力,但参数模型会受到假设条件的限制,从而影响预测准确性。因此本文考虑将RSJM参数模型与RBF神经网络非参数模型结合,提出一种针对突发事件影响下的欧盟EUA碳排放权期权定价模型。
除了单一的定价模型外,数据预处理在期权定价预测中必不可少,其中特征提取最为重要,特征提取大体上可分为价格序列分解和外部影响因素筛选。根据数据的多频率特性,Chevallier [24] 将经验模态分解算法(EMD)应用于欧盟碳排放权期权价格中,将碳排放权期权价格分为8个IMFs分量和1个趋势项,提出了对于碳排放权期权价格预测的相关策略,但后来发现EMD算法存在模态混叠问题;为了解决此问题,TORRES等 [25] 提出了一种改进算法CEEMDAN,该方法通过多次试验抵消分解过程中噪声的影响,从而得到相对纯净的分解序列。现有研究表明 [26] [27],将经CEEMDAN算法分解子序列纳入输出结果的预测模型中,由于没有考虑到它们之间相似的复杂性和相关性,从而降低了效率和准确性,因此对分解后相关性较强的序列进行重构十分必要。另外,实物期权具有高度复杂性 [28],需要考虑不同期权之间的相互作用,又考虑到实物期权收益的不确定性,即受到宏观经济变量的影响,到目前为止,文献鲜见将外部影响因素引入到碳排放权期权定价模型中,因此本文的研究目的之一是验证其合理性。
基于以上所述,本文主要讨论新冠肺炎疫情下的碳排放权期权定价;针对碳排放权期权与金融期权的不同之处,提出基于LGBM [29] 和AE [30] 序列重构的特征提取方法,充分考虑到了碳排放权期权收益的不确定性和先后关联性,有效地筛选出影响碳排放权期权的重要特征;为了解决单一模型的片面性 [31] [32] [33] 和突发事件的影响,本文提出将RS-跳扩散参数模型与RBF神经网络非参数模型相结合,与GARCH-FBM模型相比具有较高预测精度和较强稳健性。
2. 模型的建立
利用LGBM特征筛选、CEEMDAN价格分解以及AE序列重构算法得到碳排放权期权价格的重要影响因素,构建不同维度下的RSJM-RBF组合预测模型。基本预测框架如图1所示:
2.1. LGBM特征工程
针对欧盟碳排放权期权的先后关联性和收益的不确定性,综合已有文献研究 [34] [35],本文选取了如表1所示的指标来对碳排放权期权价格进行预测。为了得到最优影响因素,使用LGBM对待选因素进行特征重要性排序。
上述特征只考虑到外部因素的影响,忽略了价格序列本身的特征,故本文利用CEEMDAN和AE对碳排放权期权价格进行分解和重构,将其直接作为影响碳排放权期权价格的内在影响因素,以期提高预测精度。
2.2. 机制转换的跳–扩散模型(RSJM)
RSJM下的碳排放权期权价格公式为 [36]:
(1)
为正常经济状态下累积逗留时间的条件概率密度。
(2)
(3)
其中,
是到期时间为T,敲定价格为K,波动率为
,利率为
的标准BS期权定价公式。
(4)
(5)
t和
为正常经济状态(
)和重大事件发生时经济状态(
)的累积逗留时间,
和
分别为两种状态下跳跃次数,总跳跃次数为
。

Table 1. List of features to be selected
表1. 待选特征列表
2.3. RBF神经网络模型
基于RBF神经网络模型在实物期权定价中的良好表现,即训练速度快,不容易陷入局部最优值等优点,本文将其纳入研究中。另外,目前关于期权定价的研究方法主要从以下两个角度来考虑:基于历史数据本身的期权定价和基于外部影响因素的期权定价;由于单一模型的预测往往具有片面性,综合利用基于两种角度的RBF神经网络模型的输出信息,赋予不同权重,即误差小的权重高,误差大的权重低,再将两种输出结果进行融合,不但能提高预测精度还能获得稳定输出。
最优权重可通过构建以下方程组求得 [37]:
(6)
其中,
是实际碳排放权期权价格,
是各模型的预测价格,
是加权系数,最终预测值为:
(7)
3. 实证分析
3.1. 数据来源
为评价所提混合模型在碳排放权期权定价研究中的有效性和实用性,本文以2019年12月~2021年12月欧盟碳排放配额EUA期货期权合约日收盘价作为研究对象,到期日为2021年12月21日,部分实验数据如表2所示。
为研究疫情下碳排放权期权价格的波动情况,本文针对欧盟每日确诊病例数,将疫情分成了四个时期,分别为疫情形成期(2019.12.6~2020.3.29)、一次爆发期(2020.3.30~2020.10.29)、疫情波动期(2020.10.30~2021.6.15)和二次爆发期(2021.6.16~2021.12.7),如图2所示。
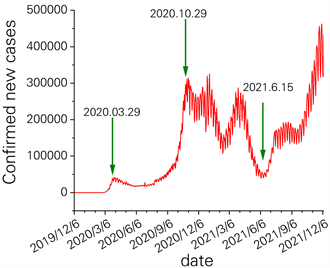
Figure 2. Number of daily confirmed cases in EU
图2. 欧盟每日确诊病例数
3.2. 特征筛选
本文使用LGBM回归算法对表1所选变量进行特征重要性筛选,由于不同时期碳排放权期权价格具有不同的特性,因此在利用LGBM进行筛选时,所选参数也不同,具体参数如表3所示:

Table 3. Parameter settings of LGBM regression algorithm in different periods
表3. LGBM回归算法在不同时期的参数设置
基于以上参数设置,使用python中的SK-learn框架下LGBM回归算法进行特征重要性筛选,结果如图3~6所示:

Figure 3. Importance of characteristics of epidemic formation period
图3. 疫情形成期特征重要性
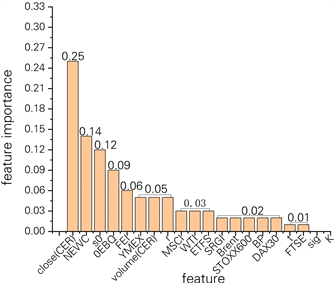
Figure 4. Importance of characteristics of an outbreak period
图4. 一次爆发期特征重要性
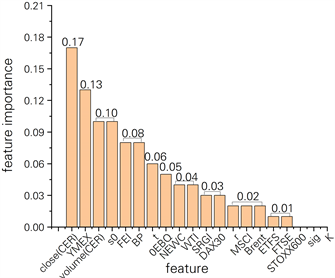
Figure 5. Importance of epidemic fluctuation period characteristics
图5. 疫情波动期特征重要性

Figure 6. Importance of characteristics of secondary eruption period
图6. 二次爆发期特征重要性
为了保持模型的精度和稳健性,本文选取在四种时期重要性均大于等于0.03的特征进行后续模型的实验,即本文最终选取开盘价(S0)、欧盟CER收盘价(close)、纽卡斯尔动力煤现货价(NEWC)、法国电力指数(FEI)来对碳排放权期权价格进行预测。
3.3. 数据分解与重构
通过CEEMDAN对欧盟碳排放权期权价格进行分解,得到5个IMF和1个趋势项,结果如图7所示,随后利用AE信息熵算法重建了分解后的子序列,分解序列和重构序列的相关统计指标如表4和表5所示。

Table 4. Statistical indicators of each component
表4. 各分量的统计指标
从表4可以看出,IMF1-IMF4与碳排放权期权价格的相关系数都不高,在肯达尔相关系数、皮尔逊相关系数和斯皮尔曼相关系数的研究中都远小于IMF5和趋势项与碳排放权期权的相关性,为了提高各分量和趋势项的应用价值,本文考虑将各分量进行重构得到AE1 (IMF1, IMF4)、AE2 (IMF2, IMF3)和AE3 (IMF5, R),重构后的统计指标如表5和图8所示。

Table 5. Statistical indicators of each reconstructed sequence
表5. 各重构序列的统计指标
对比表4,可以看出重构后三种相关系数比重构前有了明显提高。从而提高了各分量和趋势项对碳排放权期权价格的影响程度,对后续的准确预测提供了较大帮助。
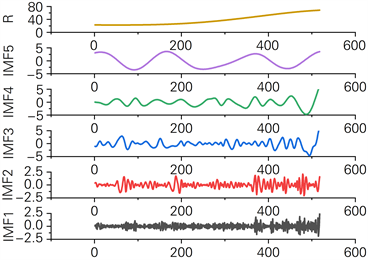
Figure 7. EU EUA price breakdown sequence diagram
图7. 欧盟EUA价格分解序列
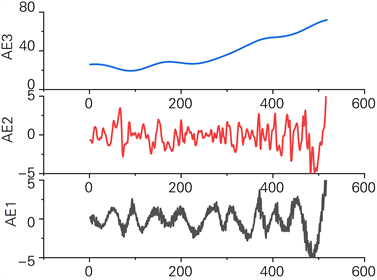
Figure 8. Approximate entropy reconstruction sequence of each subsequence
图8. 各子序列的近似熵重构序列
3.4. 欧盟碳排放权期权价格实证分析
不同的时间序列数据有适合的预测模型,可以通过不同的参数值区分。在RBF神经网络模型中,内部参数的选择是影响其模型泛化能力的重要因素,因此,本文经过多次反复训练得到不同纬度下RSJM-RBF模型的最佳超参数。各维度下模型重要参数如表6所示。

Table 6. Important parameters of each model
表6. 各模型重要参数
为了直观地判断每个模型的预测效果,本文选择了三个常用的误差评价指标来衡量模型的性能。较低的平均绝对百分比误差(MAPE)更符合预期,均方根误差(RMSE)用来测量观测值和实际值之间的偏差,如果模型拟合得更好,拟合优度(R2)将更接近1。评价指标的计算公式如下:
(8)
其中,
表示真实碳排放权期权价格,
表示预测的碳排放权期权价格,
表示碳排放权期权价格的均值,n表示样本数量。
为了验证本文所提模型的有效性,选择了GARCH-FBM、不同特征下的RSJM-RBF权重组合模型进行对比实验。如图9,给出了两个模型的预测对比结果,如表7,给出了四个模型的性能比较结果。

Figure 9. Comparative results of two models
图9. 两种模型的对比结果

Table 7. Performance comparison of different prediction models of EU carbon option price
表7. 欧盟碳排放权期权价格不同预测模型的性能对比
实验结果表明,本文所提模型的预测精度要优于GARCH-FBM模型,其中MSE提高了0.1257,拟合优度达到0.9980。由图9上知,在整个二次爆发时期,只有一个阶段(2021.6.22~2021.7.22)出现较为明显的波动,且波动后碳排放权期权价格整体呈降低趋势,由于碳排放权期权市场具有短暂的滞后效应,观察图9下,Weight Combination Model能够快速响应期权价格波动初期的震荡情况,进而准确预测出波动位置和幅度。而GARCH-FBM模型响应相对缓慢,预测也呈低估趋势。
除了通过以上评估指标来对模型的精度进行分析外,模型鲁棒性研究也极为重要,为了评估不同模型在随机扰动下的稳健性,本文通过对不同模型中对碳排放权期权价格影响最大的特征随机添加100次相同扰动项,并求出不同模型预测结果与真实期权价格之间的皮尔逊相关系数,具体结果如图10和图11所示。
在无随机干扰的情况下,本文所提模型和GARCH-FBM模型两者的预测结果与真实期权数据之间的相关系数分别为0.99和0.994,由图10可看出,本文所提混合模型的预测结果最稳定,相关系数在0.99~0.994之间,而GARCH-FBM在100次随机干扰下相关系数有明显降低,因此本文所提模型的鲁棒性要优于GARCH-FBM模型。
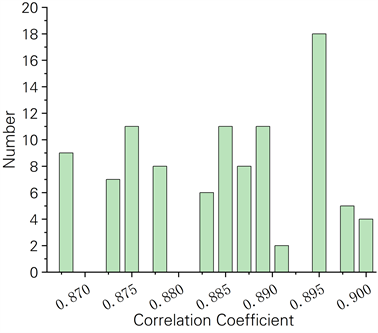
Figure 10. Robustness analysis of GARCH-FBM model
图10. GARCH-FBM模型鲁棒性分析

Figure 11. Robustness analysis of weight combination model
图11. 权重组合模型的鲁棒性分析
4. 结论
本文将新冠肺炎疫情与碳排放权期权价格联系起来,针对疫情下碳排放权期权价格波动较大,滞后性明显等特点,将参数模型和非参数模型结合,充分利用各模型的优点,提出了不同特征维度下RSJM-RBF神经网络模型,与GARCH-FBM模型对比具有较高的预测精度,且本文所提模型的稳定性要优于参照模型,本文研究具体表现如下:
(一) 针对疫情下碳排放权期权数据的特性,借助于LGBM特征筛选和AE序列重构算法,建立了不同特征维度下RSJM-RBF神经网络模型。
(二) 本文所建模型能够快速响应突发事件下的碳排放权期权价格变化情况,预测精度和鲁棒性均优于参照模型,且比参照模型更能准确预警到期权价格的波动位置和波动幅度。
(三) 根据LGBM特征筛选,同类替代产品中CER结算价和电力价格在不同时期的重要性并未受到较大影响,且一直处于重要地位。宏观经济在各个时期重要性持续处于较低位置,一次能源价格在疫情前重要性显著,疫情爆发之时,重要性整体有所降低。B-S特征中的开盘价在疫情前影响不大,疫情后影响显著。
因此,后期应着重关注同类替代产品、电力价格和EUA收盘价对碳排放权期权的影响,也可将气候因素和投资者情绪等因素考虑在内,以此建立优化后的碳排放权期权定价模型,给决策者和投资者提供更为合理的指导作用。
基金项目
国家自然科学基金(51675161)。