结合个体情绪因素的人群运动仿真

Simulation of Crowd Motion Combined with Individual Emotional Factors

摘要: 尽管现在的疏散模型逐渐开始考虑情绪对人群疏散的影响，但是大多数研究的重点在于情绪是如何在人群中传播，很少考虑个体在不同情绪下的行为特点。而显然，行人在不同情绪状态下的行为特征是不同的。因此，在考虑情绪对人群的影响时不应该忽略情绪差异对个体行为模式带来的影响。针对该问题，提出了一种将个体情绪因素与个体行为特征相结合的仿真方法。首先，个体按照情绪进行分类并归纳不同情绪行人的行为特征。其次，结合个体的情绪因素计算出行人在人群中的情绪力。最后，将情绪力与社会力模型相结合，共同驱动人群的运动。

Abstract: Although current evacuation models have gradually begun to consider the influence of emotion on crowd evacuation, most research focuses on the contagion of emotion in crowds, and rarely considers the behavioral characteristics of individuals under different emotions. Obviously, the behavior characteristics of pedestrians in different emotional states are different. Therefore, the impact of emotional differences on individual behavior should not be ignored when considering the impact of emotions on the crowd. This article proposes a simulation method that combines individual emotional factors with individual behavior characteristics. Firstly, individuals are classified according to their emotional states and summarized the behavior characteristics of pedestrians with different emotions. Secondly, the emotional force of pedestrians in crowds is calculated based on their emotional state. Finally, the emotional force and social force model are combined to drive the movement of crowds.

1. 引言

人群运动建模和仿真是计算机图形学 [1]，安全科学 [2] 和人工智能 [3] [4] 的研究热点，已被用于许多应用领域，例如人群疏散 [5]，数字娱乐 [6] 和社会保障 [7] [8]。人群仿真可以很好地再现人群运动的自组织现象 [9] - [14]，同时结合个体的生理特征、社会因素等各种不确定因素，可以更准确地模拟紧急情况下人群的疏散行为。

在现实生活中紧急情况经常导致行人精神紧张。而这些负面情绪很容易在人群中散布开来，最终可能导致大规模的人群骚动。因为情绪是个体的认知和意识一起产生的一种心理活动，它不仅影响个体自身的行为，而且可以通过情绪传染来影响其他个体的行为。因此，模拟在情绪影响下的人群疏散是一个非常具有挑战性的问题。Fu等人 [15] 将SIR模型引入元胞自动机模型并开发了“CA-SIRS”模型。该模型通过模拟人群在静止和运动下的情绪传染情况，发现个体运动会增加情绪传染的速度，并增加最终受感染行人的比例。Cao等人 [16] 将P-SIS模型与社会力量模型相结合，发现该模型可以更真实地模拟人群疏散。Xu等人 [17] 探究了密集人群中情绪传染过程的动力学，研究了初始消极情绪行人的比例，情绪影响半径等因素对人群情绪转变的影响。

纵观当前的研究，可以发现大多研究侧重于情绪的传播过程及人群情绪的演变对人群疏散的影响，而少有文章关注个体行为对人群的影响 [15] [16] [17] [18] [19]。显然个体在不同情绪下具体行为方式的差异也同样会影响情绪的传染以及人群的疏散。Xiong等人 [20] 使用了一种速度优先采样的方法来模拟不同情绪下行人的运动，他们根据情绪的差异，对行人的运动方向划分不同的优先级，情绪越不稳定的行人越趋向于以一个更快的速度，更小的绕行弧度超越前方的行人。而传统的社会力模型并不能体现出不同情绪个体的行为差异。因此，有必要对传统社会力模型进行相关改进。Ge和Cui引入了一种分数阶势场的方法 [21]，应于机器人的路径规划，他们通过控制阶数的变化来调整机器人与不同危险程度障碍物的互动情况。Stuart等人 [22] 也曾通过分数阶势场对残疾人这一特殊群体与普通行人间的互动情况进行仿真模拟。本文从中获得启发，并将其拓展至结合情绪的人群仿真领域，对原有的社会力模型进行改进，提出了一种结合分数阶势场的人群运动仿真方法，从力学的角度对这种情绪带来的差异性进行描述与分析。首先，我们将个体的情绪状态进行分类，并对不同情绪状态的行人设置期望速度，视域范围等相关参数；然后，分析传统社会力的缺陷并引入分数阶势场用以描述情绪差异；最后将情绪属性注入到传统社会力中得到最终的情绪模型，并通过该模型进行仿真来验证其有效性。

2. 行人情绪类别划分

社会科学研究调查了行人在社交活动中如何管理与其他行人的距离。距离被分成四个区域：亲密距离、私人距离、社交距离、公共距离 [23]。而在日常生活中，我们常常可以发现不同情绪状态的行人在面对障碍时会采取不同的行为策略从而动态地调整他们之间的距离，特别是车站大厅等场所尤其明显。情绪状态稳定的行人在超越前方行人时往往会以采取一个适宜的距离；而如果行人稍有焦虑，则可能更倾向于以一个较小的距离超越前者；而当焦虑程度较高，则会进一步减小绕行距离；而当行人非常迫切地想离开时，则会紧挨着前方行人进行绕行，从而减少离开时间。基于这一点，我们将行人根据其情绪状态及相关特征进行总结并分类。

在本文中，情绪焦虑程度的强度用E表示。我们将随机生成的E赋予给各个个体用来划分情绪状态。对于每一个个体，情绪值E处于区间(0, 1]。我们将个体的情绪值分为对应不同情绪状态的四个级别 [24]，同时对行人速度做了相关设定 [23]。

另外，我们注意到情绪和注意力的相互作用会影响基本的视觉功能 [25]。很多研究者探讨积极情绪状态对认知的影响，发现积极情绪会导致认知范围的扩展 [26]，而消极情绪状态则会使注意窄化 [27]。整体–局部视觉性加工范式的研究也同样发现，处于积极情绪体验的个体更偏向于注意整体结构 [28]。因为积极情绪意味着一种稳定的舒适的环境，因此会促使个体的注意范围和认知范围更开阔 [26]。Fredrickson [26] 也发现两种积极情绪状态下的个体比中性状态的个体有更广的注意范围。在积极情绪扩展建构理论中，积极情绪本身具有拓展作用。国内也有一系列的研究证实积极情绪确实拓宽注意范围，使注意更加灵活 [29]。一系列的研究证实积极情绪对空间注意范围、时间注意范围有扩展作用。

而对于消极情绪，研究人员认为其对注意范围的影响与积极情绪对注意范围的影响方向相反 [26]。具体地说，消极情绪状态使注意窄化 [27]。因为消极情绪意味着不稳定和不舒适的环境，会使个体的认知加工有局部性和分析性 [28]，因此个体的注意会更加集中，从而窄化注意范围，许多研究证实了这一理论。

据此，我们将这种注意范围随情绪变化的规则融入我们的模型，并将注意范围定义成扇形视域范围。因为在传统的模型中仅仅是将行人的视域设定为180˚，并没有考虑到个体的真实视域并非是固定不变 [30]，每个人的视域会随着情绪的变化而发生转变。基于前文的研究结果 [25] [26] [27] [28]，根据视域范围随焦虑程提高而窄化的特点，对不同情绪下的注意范围进行相关设定。具体信息如表1和图1所示。

Table 1. Emotional state reference table

表1. 情绪状态参照表

如图1所示，a行人表示此时其情绪状态为Calm，在当前情绪状态下注意范围最广，为180˚；b行人的情绪状态为Anxiety，其注意范围相较a行人而言有所变小，此时的注意范围为135˚；随着焦虑程度的提高，行人的注意范围进一步缩小为90˚，此时的情绪状态为Panic，如c行人所示；d行人显示当情绪状态为Hysteria时，注意范围最小，为45˚。可以看出，随着焦虑程度的提高，注意范围注意变窄，行人的注意力逐渐聚集到自己的正前方，此时虽然个体的行进速率增加了，但与周围行人发生碰撞的概率也增加了。

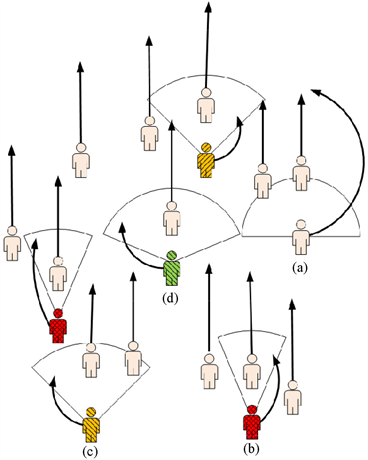
Figure 1. Pedestrians in different emotions

图1. 不同情绪下的行人示意图

3. 结合情绪表达的社会力模型

传统社会力模型只能表示行人的基本运动情况，并不能体现不同情绪状态下行人的差异性，为了描述出不同情绪下的行人的运动差异，我们在传统社会力的基础上通过分数阶势场对其进行改进。因此本文的模型由传统的社会力模型与情绪力两部分组成。

3.1. 传统社会力模型

社会力量模型是由Helbing等人 [10] 提出的用以描述行人运动的模型，是一种经典的连续空间微观模型 [10] [31] [32] [33] [34]。该模型包含三种力：朝向目标的驱动力，来自相邻行人的排斥力，来自障碍物的排斥力，其等式为：

$m_i\frac{\text{d}{\stackrel{\to }{v}}_i\left(t\right)}{\text{d}t}={\stackrel{\to }{f}}_i^0+{\displaystyle \underset{j\left(\ne i\right)}{\sum }{\stackrel{\to }{f}}_{ij}}+{\displaystyle \underset{w}{\sum }{\stackrel{\to }{f}}_{iw}}$ (1)

其中

${\stackrel{\to }{f}}_i^0\left(t\right)=m_i\frac{v_i^0\left(t\right){\stackrel{\to }{e}}_i^0\left(t\right)-{\stackrel{\to }{v}}_i\left(t\right)}{{\tau }_i}$ (2)

${\stackrel{\to }{f}}_{ij}=\left(A_i\exp \left(\frac{r_i+r_j-d_{ij}}{B_i}\right)+KG\left(r_i+r_j-d_{ij}\right)\right){\stackrel{\to }{n}}_{ij}+kG\left(r_i+r_j-d_{ij}\right)\Delta v_{ij}^t{\stackrel{\to }{t}}_{ij}$ (3)

${\stackrel{\to }{f}}_{iw}=\left(A_w\exp \left(\frac{r_i-d_{iw}}{B_w}\right)+KG\left(r_i-d_{iw}\right)\right){\stackrel{\to }{n}}_{iw}+kG\left(r_i-d_{iw}\right)\left({\stackrel{\to }{v}}_i\cdot {\stackrel{\to }{t}}_{iw}\right){\stackrel{\to }{t}}_{iw}$ (4)

${\stackrel{\to }{n}}_{ij}=\frac{1}{d_{ij}}\left({\stackrel{\to }{r}}_i-{\stackrel{\to }{r}}_j\right)=\left(n_{ij}^1,n_{ij}^2\right)$ (5)

${\stackrel{\to }{t}}_{ij}=\left(-n_{ij}^2,n_{ij}^1\right)$ (6)

$\Delta v_{ij}^t=\left({\stackrel{\to }{v}}_j-{\stackrel{\to }{v}}_i\right)\cdot {\stackrel{\to }{t}}_{ij}$ (7)

对于每个行人 $i$，其运动是由下列各项共同决定的：1) 行人的驱动力 ${\stackrel{\to }{f}}_i^0$ ；2) 来自其他行人的社会力 ${\stackrel{\to }{f}}_{ij}$ ；3)来自墙的力 ${\stackrel{\to }{f}}_{iw}$。这些力已由公式(2)至(4)给出，与Haghani和Sarvi [35] 提出的公式一致。在这些方程式中， $m_i$ 表示体重， ${\stackrel{\to }{v}}_i\left(t\right)$ 表示速度矢量，并重新定义行人的位置矢量 $i$。矢量 ${\stackrel{\to }{e}}_i^0\left(t\right)$ 和 $v_i^0\left(t\right)$ 分别表示行人的期望方向和期望速度值。值 $r$ 和 $d_{ij}$ 分别代表行人的身体半径和行人之间的距离。当函数 $G\left(r_i+r_j-d_{ij}\right)$ 的参数为正时，它是一个恒等函数，否则返回值0。 ${\stackrel{\to }{n}}_{ij}$， ${\stackrel{\to }{t}}_{ij}$， $\Delta v_{ij}^t$ 分别由等式(5)，(6)和(7)定义。 $d_{iw}$ 的定义与此类似，它表示行人与墙壁之间的距离。另外， ${\tau }_i$ (松弛参数)， $A_i$， $B_i$， $A_w$， $B_w$， $k$ 和 $K$ (摩擦力参数)都是自定义的参数。

3.2. 分数阶下的情绪表达

分数阶势场由于其优雅的数学分析和表达而广泛的应用于机器人路径规划 [21] [36]。一般而言，势场的形状和距离都取决于等式的形式，而分数势场可以通过改变阶数来直接改变势场形状，从而得到我们需要的势场模型。此外，分数阶势场在计算势场的过程中是不需要进行积分运算的，因此势场的形状只取决于阶数n且最终的表示形式非常简洁。本文将其拓展至体现情绪因素的人群运动仿真，通过阶数的变化，来控制异质性人群的运动方式。在本文中我们称之为“情绪场”。根据相关数学推导 [21] 我们可以得到情绪场的表达公式：

$U_{drep}\left(r\right)=\frac{r^{n-2}-r_{\max }^{n-2}}{r_{\min }^{n-2}-r_{\max }^{n-2}}$ (8)

其中当 $n=2$ 时，

$U_{drep}\left(n=2\right)=\frac{\ln \frac{r}{r_{\max }}}{\ln \frac{r_{\min }}{r_{\max }}}$

其中 $U_{drep}\left(r\right)$ 表示势场， $n$ 表示阶数，反映的是异质性群体的情绪值， $n$ 越大情绪越不稳定。 $r_{\max }$ 表示情绪力作用的最大有效距离， $r_{\min }$ 表示情绪力的最小有效距离， $r$ 表示两个行人之间的距离。

势场的负梯度即为在势场中的受力，本文称之为“情绪力”，其表达式为：

$F_{d_{ij}}=-\frac{\left(n-2\right){\Vert {\stackrel{\to }{r}}_{ij}\Vert }^{n-3}}{r_{\max }^{n-2}-r_{\min }^{n-2}}$ (9)

其中 $F_{d_{ij}}$ 表示情绪力的大小， ${\stackrel{\to }{r}}_{ij}$ 表示两个行人之间的距离。

根据分数阶势场模型可以通过控制阶数 $n$ 改变势场形状以及排斥力随距离变化的特点，我们将分数阶势场引入到社会力模型中去，并将其重新定义成符合人群运动规律的情绪场模型。在情绪场模型中，我们将 $r_{\min }$ 设置成1，将 $r_{\max }$ 设置成5，同时令 $1\le n\le 5$，得到情绪场曲线如图2所示。

观察势场曲线图可以发现，随着行人间距离的不断缩短，对于情绪稳定的行人，势场线越来越陡峭，其所受情绪力剧烈增加，说明情绪状态稳定的行人更趋于保持一个比较舒适的空间距离；而对于不稳定的行人而言，情绪力的增速逐渐减慢，势场线由凹函数向凸函数过渡，这表明行人开始减少对自我空间

Figure 2. Emotional potential field curve graph

图2. 情绪势场曲线图

的需求。当焦虑程度到达一定值，行人会为了尽快到达目标地点而放弃对舒适空间的追求，此时势场线呈现明显的凸函数形状，此时的情绪力随着距离的缩短反而越来越小。通过为不同情绪状态的行人分配不同的情绪值 $n$，行人可以对视域范围内的阻碍采取不同的运动策略。

3.3. 结合情绪表达的社会力模型表示

根据分数阶势场模型可以通过控制阶数改变势场形状以及行人间排斥力随距离变化的特点，我们在传统社会力的基础上加上了情绪力的作用，用以刻画不同情绪状态下行人的运动情况，得到了最终的公式：

$m_i\frac{\text{d}{\stackrel{\to }{v}}_i\left(t\right)}{\text{d}t}={\stackrel{\to }{f}}_i^0+{\displaystyle \underset{j\left(\ne i\right)}{\sum }{\stackrel{\to }{f}}_{ij}}+{\displaystyle \underset{w}{\sum }{\stackrel{\to }{f}}_{iw}+}{\displaystyle \underset{j\left(\ne i\right)}{\sum }{\stackrel{\to }{F}}_{d_{ij}}}$ (10)

为了验证情绪模型的有效性，我们首先通过最简单的实例来展示本文模型的仿真效果。如图3所示，在该场景中，我们设置两个行人，其中一个行人始终保持直线行走，另一个不同情绪的行人以不同的轨迹超过前方行人，实线表示在视域均为180˚时行人的运动轨迹。当 $n=1.7$ 时，黑色小人表示情绪状态为Calm，他趋于保持一个舒适的空间，因此他会以一个较大的半径从侧面绕过前方的行人；当 $n=2.5$ 时，行人的焦虑程度变高，此时他开始减少个人空间的需求，在越过前方行人时所需的半径有所减小；随着行人焦虑程度的不断累积，他更加迫切绕过前方的行人，需求的个人空间也越来越小(如 $n=3.2$ 所示)，最终当 $n=4.5$ 时，该行人几乎是紧挨着前方的行人进行绕行。

在情绪力的基础上，我们进一步加上了视域的影响，对不同情绪状态的行人设定了不同的视域范围。如图3所示，虚线表示不同情绪行人在不同视域作用下的运动轨迹，其中 $n=1.7$ 时视域范围为180˚， $n=2.5$ 时视域为135˚， $n=3.2$ 时视域为90˚， $n=4.5$ 时视域为45˚。可以发现，行人的运动轨迹进一步发生了变化。由于当 $n=1.7$ 时，行人的情绪状态为Calm，视域始终为180˚，所以此时运动轨迹没有发生变化；而当 $n=2.5$ 时，行人在绕开一定距离后，前方行人由于消失在后者的视域范围内，所以后方行人不再受到情绪力的影响，因此更早的停止绕行。随着 $n$ 的逐渐增大，视域范围逐渐变窄，后方行人受到前方行人影响的时间逐渐减少，因此更趋向于保持原前进方向。可以看出，该仿真结果符合提出的不同情绪行人的行为差异。

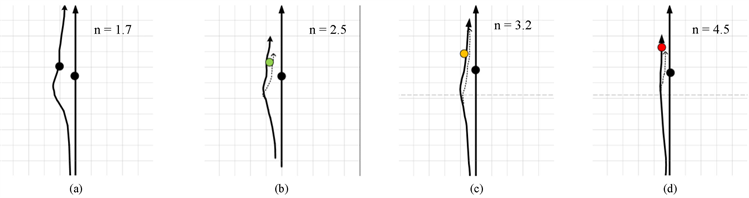
Figure 3. The difference of pedestrians’ trajectories in different states

图3. 不同情绪状态行人绕行差异图

4. 研究结果及讨论

本文基于Unity 3D仿真平台，构建了单出口和多出口疏散场景，利用本文所提方法模拟人群运动，并与传统社会力模型进行对比，验证所提方法的有效性。

4.1. 单出口疏散场景

疏散场景设置为15 × 20 m²的单出口房间，其中出口宽度为1.4 m [37]。场景中的总人数为200人，行人的质量设置为70 kg，行人的速度的设置参考表1，其他参数变量如下所示：A_i = 2000 N，A_w = 2000 N，K = 1.2 × 10⁵ kg∙s⁻²，k = 5.4 × 10⁵ kg∙m⁻¹∙s⁻¹，B_i = 0.1 m，B_w = 0.08 m。

4.1.1. 单一情绪下传统社会力与本文所提方法比较

为了探究传统社会力模型和本文所提方法对人群运动影响，我们模拟了单出口下的人群疏散行为，并展示了t = 0 s，t = 6 s，t = 20 s，t = 32 s四种分布状态。其中，行人的速度均设置为1 m∙s⁻¹，本文方法中的行人情绪状态均设置为Calm。图4和图5展示了本文方法和传统社会力方法下行人在疏散过程中位置分布差异。

如图4(a)和图5(a)所示，每个行人的初始疏散位置是相同的。然而，由于本文所提的模型中，行人之间存在情绪力，所以场景中的行人之间都会保持相对舒适的空间距离，如图4(b)和图5(b)所示。随着疏散过程的进行，场景中的行人涌向出口，可以发现，传统社会力模型下在出口处会更早的出现阻塞现象，而本文所提方法在相同时刻却并没有出现这种现象，如图4(c)和图5(c)所示。这是由于在情绪力的作用下，情绪状态稳定的行人并不会为了离开房间而放松自己对空间的要求，而这也促使了行人有序的离开房间而不会出现大面积的阻塞现象。值得注意的是，两种方法最终的疏散效率差异不大，如图4(d)和图5(d)。分析这种情况的原因在于，虽然传统社会力模型下的行人相比较本文方法而言，行人没有受到情绪力的作用而去保持一定的空间距离，这使得他们可以更快地到达出口处，但他们在出口处形成了明显的阻塞区域，由于“快即是慢”效应，反而使得人群的疏散效率有所下降，最终导致了两种方法在疏散效率上差异不大。

4.1.2. 多情绪下传统社会力与本文所提方法比较

为了探究多种情绪状态下传统社会力模型和本文所提方法间人群运动行为的差异，我们模拟了单出口下人群的疏散行为，并展示了t = 0 s，t = 6 s，t = 10 s，t = 19 s四种分布状态。图6和图7展示了本文方法和传统社会力方法下行人在疏散过程中位置分布差异。其中，黑色行人表示情绪状态为Calm，速度为1 m∙s⁻¹；绿色行人表示情绪状态为Anxiety，速度为1.5 m∙s⁻¹；黄色行人表示情绪状态为Panic，速度为2 m∙s⁻¹；红色行人表示情绪状态为Hysteria，速度为2.5 m∙s⁻¹。

Figure 4. Location distribution of the proposed method at different time: (a) t = 0 s; (b) t = 6 s; (c) t = 20 s; (d) t = 32 s

图4. 本文模型在(a) t = 0 s，(b) t = 6 s，(c) t = 20 s，(d) t = 32 s时的位置分布图

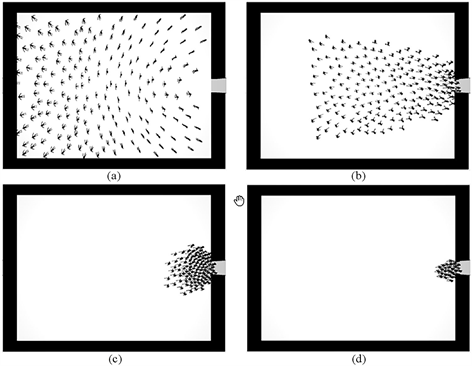
Figure 5. Location distribution of SFM at different time: (a) t = 0 s; (b) t = 6 s; (c) t = 20 s; (d) t = 32 s

图5. 传统社会力模型在(a) t = 0 s，(b) t = 6 s，(c) t = 20 s，(d) t = 32 s时的位置分布图

如图6(a)和图7(a)所示，每个行人的初始位置是相同的。在本文所提模型中，不同情绪状态的行人在面对障碍时会采取不同的绕行措施，而传统社会力模型在体现情绪变化时只改变了不同情绪状态行人的速度 [10]，如图6(b)和图7(b)所示，这导致焦虑行人在遇到阻碍时往往会由于绕行不及时而导致与前方行人发生碰撞，甚至出现尾随在前方行人后面等不合理的现象，而本文的方法中，行人会采取一个适合的弧度进行绕行。随着疏散的进行，传统情绪模型也先行出现的较长的阻塞，而本文模型下的行人在出口处分布更均匀，如图6(c)和图7(c)所示。

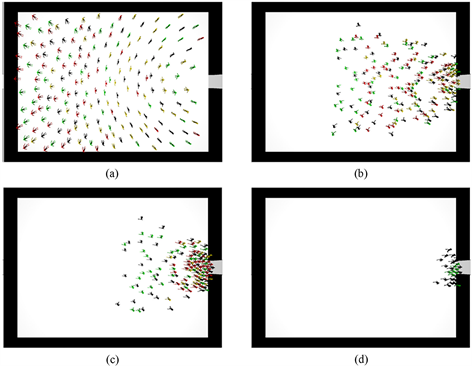
Figure 6. Location distribution of the proposed method at different time: (a) t = 0 s; (b) t = 6 s; (c) t = 10 s; (d) t = 19 s

图6. 本文模型在(a) t = 0 s，(b) t = 6 s，(c) t = 10 s，(d) t = 19 s时的位置分布图

Figure 7. Location distribution of SFM at different time: (a) t = 0 s; (b) t = 6 s; (c) t = 10 s; (d) t = 19 s

图7. 传统社会力模型在(a) t = 0 s，(b) t = 6 s，(c) t = 10 s，(d) t = 19 s时的位置分布图

进一步的，我们对无情绪传统社会力模型、多情绪传统社会力模型以及本文模型进行了定量分析，如图8所示。可以得到的是，包含情绪变化的传统社会力模型与本文所提模型的疏散效率都远高于不包含情绪变化的传统社会力模型。进一步分析多情绪传统社会力模型与本文模型，结合图6(b)、图7(b)可知疏散初期的出口处并没有形成严重的阻塞现象，行人的疏散行为不会受到明显阻碍，因此此时两种模型的疏散效率相差不大。但在疏散中期，本文所提模型的疏散效率要高于传统的情绪模型，由图6(c)和图7(c)可以看出，此时传统社会力模型的出口处出现了较长的阻塞队列，而本文模型中的行人在出口两侧均匀分布，避免了长队列的产生。最后，在疏散末期，在出口处压力不大的情况下，本文模型的行人由于要保持一定的空间距离，因此在最终的疏散效率上稍慢于多情绪传统社会力模型。

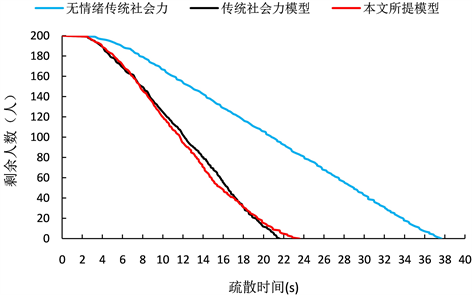
Figure 8. Comparison of evacuation efficiency under different models

图8. 不同模型下疏散效率对比

Figure 9. Evacuation scenario with 2, 3 and 4 exits respectively

图9. 出口数分别为2、3、4的疏散场景

4.2. 多出口疏散场景

为了验证多出口场景下人群运动情况，该部分构建了三个疏散场景，分别是双出口、三出口和四出口。在这三种疏散场景中，行人的初始位置与3.1节中的单出口场景相同。在多出口场景下，所有的行人选择离自己更近的出口。在图9中，分别表示了疏散出口数量为2、3、4下t = 6 s时人群的位置分布。其中图9(a)、图9(c)、图9(e)是由本文方法驱动的，而图9(b)、图9(d)、图9(f)是由传统社会力模型驱动的。

从图9可以看出，无论出口数量是2个、3个还是4个，本文方法驱动的行人在疏散过程中会根据情绪的差异而出现不同的绕行差异，同时在出口处不会形成明显的阻塞现象。这与本文提出的情绪模型一致。此外，随着出口数量的增加，两种方法的疏散效率显著提高。

5. 结束语

本文中提出了一种基于社会力和分数阶势场的混合模型，同时融入了视域的变化，用以描述不同情绪因素下个体行为差异对人群运动的影响。通过对行人在不同情绪状态下行为差异的分析以及传统社会力模型的回顾，指出了传统社会力模型在表达情绪因素时存在的局限性。利用分数阶势场及视域变化对其进行改进，计算出不同行人的情绪力，并结合个体之间的排斥力，目的地的驱动力和障碍物的排斥力共同驱动人群的运动。在实验过程中可以观察到一些疏散行人流的行为特征：1) 行人在不同的焦虑程度下，会采取不同的绕行策略；2) 相比较传统社会力方法，本文方法下的行人更不容易在出口处形成阻塞；3) 行人的疏散效率随着出口数的增加而提高。仿真结果表明，本文方法不仅可以模拟不同情绪个体之间的交互行为，还可以有效模拟群体的疏散情况。在未来的工作中，我们将划分更丰富的情绪种类、结合情绪的传染，更深入地探索情绪变化下的人群行为。