带三参数的三次B样条扩展曲线及其应用

Cubic B-Spline Extension Curve with Three Parameters and Its Application

摘要: 为满足曲线自由设计的需求，本文对λ-B样条基和三次T-B样条基进行扩展，构造了λαβ-T-B样条基函数，定义了由该基函数生成的λαβ-T-B样条曲线，其中含有三个参数λ、α、β，构造的曲线不仅具备样条曲线的特性，还同时具备三角和代数多项式的优良性质，且具有形状可调性和更精确的逼近性；在给定条件下，形状参数有明确的几何意义，λ、β取值越大，α值越小，越能更好地逼近控制多边形；调节参数的取值，改变曲线的形状；选则恰当的控制顶点，根据参数对曲线的调节规律，确定恰当的形状参数，生成的λαβ-T-B样条曲线能较好贴近圆和椭圆；介绍了生成插值于给定数据点的λαβ-T-B样条曲线的构造方法，并给出具体数例的计算，验证了方法的有效性和可行性。

Abstract: In order to meet the requirement of free curve design, this paper extends the λ-B-spline basis and cubic T-B-spline basis and constructs a group of λαβ-T-B-spline basis function. The λαβ-T-B-spline curve generated by the base function is defined, which contains three parameters λ , α, and β, has the characteristics of spline basis function, but also has the good properties of trigonometric and algebraic polynomial basis, and has the shape tunability and more accurate approximation; under given conditions, shape parameters have clear geometric meaning. The larger the value λ of and β, the smaller the value of , the better the approximation control polygon can be. By changing the value of shape parameters, the curve can be adjusted; by selecting the appropriate control vertex and the appropriate shape parameters, the generated λαβ-T-B-spline curve can approach the circle and ellipse very well; In the end, the method of constructing λαβ-T-B-spline curve interpolating in the data points is introduced, and the calculation of specific numerical examples is given, reflect the effectiveness and feasibility.

1. 引言

B样条在计算机辅助几何设计中一直处于重要地位，由于其结构简单又具有灵活性，在工程实际中应用较为广泛，在文献中也有较多讨论与研究。但在曲线形状调整这一方面一直需要改进，若需调节所生成的曲线，通常仅能通过调节控制顶点来完成，这也带来些许不便。因而，不断有新的构造方法被提出。

为扩大B样条形状表示范围，学者们选择利用多项式空间 [1] [2] [3] [4] 与非多项式空间 [5] [6] [7] 进行混合，构造与B样条基类似的调配函数 [3]，由此定义的曲线的适用性有很大提高。在调配函数中，全正性 [8] 是衡量是否适用保形的标准。较多学者在过渡曲线 [9] 的基础上，将带形状参数的基函数与转换矩阵做乘积得到扩展基，证明全正性，以确定扩展基定义扩展曲线 [5] [10] - [15]。因多项式曲线的计算更为简单，可以较好地融入CAD系统。所以大多学者选择在多项式曲线上构造带有形状参数的B样条扩展曲线。利用三次或以上的调配函数，增加阶数达到形状可调性，构造的含参扩展曲线 [1] [16]，在一定条件下，能够逼近但不能精确表示圆和椭圆。

本文在 $\lambda \text{-}B$ 基 [1] 和三次T-B样条基 [5] 的基础上，给出了包含三个形状参数 $\lambda ,\alpha ,\beta$ 的三次均匀B样条扩展曲线，其中。新构造的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线保持了B样条曲线的特性，同时拥有三角和代数的优质性质，具有形状可调性和更精确的逼近性。在给定条件下，形状参数 $\lambda$ 有明确的几何意义，取值越大，越能更好的逼近控制多边形。且当 $\lambda =1$ 的时，曲线退化为 $\lambda \text{-}B$ 曲线 [1]；当 $\lambda =0$ 的时，退化为三次T-B样条曲线 [5]；当 $\lambda =1$， $\alpha =-3$，则退化为三次均匀B样条曲线。在给定恰当的控制顶点下，对 $\lambda ,\alpha ,\beta$ 做适当取值，生成的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线能够更好地贴合圆和椭圆。最后，介绍了利用 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线生成基于给定数据点的插值曲线的方案，并给出具体数例的计算，体现了新构造方法的有效性和可行性。

2. $\lambda \alpha \beta$ -T-B样条基函数的构造及性质

定义1 对 $t\in \left[0,1\right]$，令

$\{\begin{array}{l}{b}_0\left(t\right)=\lambda \frac{1}{6}{\left(1-t\right)}^2\left[1+\left(2+\alpha \right)t\right]+\left(1-\lambda \right)\frac{1}{6+4\beta }{\left(1-\sin \frac{\pi t}{2}\right)}^2\left(1-\beta \sin \frac{\pi t}{2}\right)\\ b_1\left(t\right)=\lambda \frac{1}{6}\left[4-\left(9+\alpha \right)t^2+\left(6+\alpha \right)t^3\right]+\left(1-\lambda \right)\frac{1}{6+4\beta }{\left(1+\cos \frac{\pi t}{2}\right)}^2\left(1+\beta \cos \frac{\pi t}{2}\right)\\ b_2\left(t\right)=\lambda \frac{1}{6}\left[1-\alpha t+\left(9+2\alpha \right)t^2-\left(6+\alpha \right)t^3\right]+\left(1-\lambda \right)\frac{1}{6+4\beta }{\left(1-\sin \frac{\pi t}{2}\right)}^2\left(1+\beta \sin \frac{\pi t}{2}\right)\\ b_3\left(t\right)=\lambda \frac{1}{6}{t}^2\left[\left(3+t\right)-\left(2+\alpha \right)t\right]+\left(1-\lambda \right)\frac{1}{6+4\beta }{\left(1-\cos \frac{\pi t}{2}\right)}^2\left(1-\beta \cos \frac{\pi t}{2}\right)\end{array}$ (1)

其中 $\lambda \in \left[0,1\right]$， $\alpha \in \left[-4,-1\right]$， $\beta \in \left[-\frac{1}{2},1\right]$。

称(1)式为 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条基函数。

其中三个参数 $\lambda ,\alpha ,\beta$ 取值不同时，基函数所对应图形也不同，如图1所示。

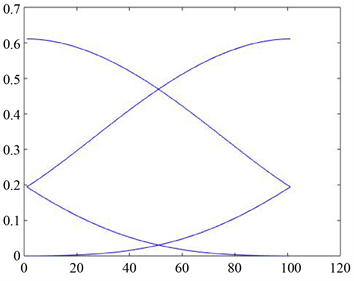
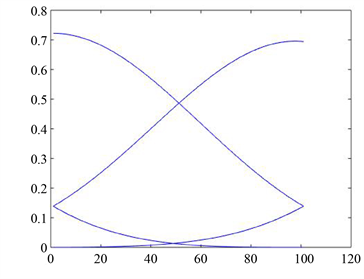
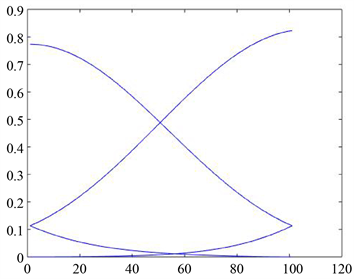
(a) $\lambda =\frac{2}{3},\alpha =-2.5,\beta =-0.5$ (b) $\lambda =\frac{1}{3},\alpha =-3,\beta =0.5$(c) $\lambda =0.2,\alpha =-1,\beta =1$

Figure 1. The graph drawn by the $\lambda \alpha \beta \text{-}T\text{-}B$ -spline basis function

图1. $\lambda \alpha \beta \text{-}T\text{-}B$ 样条基函数所绘制的图形

式(1)所表示的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条基函数有如下的性质：

性质1 退化性

当 $\lambda =1$ 的时候式(1)则退化为 $\lambda \text{-}B$ 样条基 [1]；当 $\lambda =0$ 的时候式(1)则退化为三次T-B样条基 [5]；当 $\lambda =1$， $\alpha =-3$ 式(1)则退化为三次均匀B样条基。

性质2 非负性

对任意的 $t\in \left[0,1\right]$， $\lambda \in \left[0,1\right]$， $\alpha \in \left[-4,-1\right]$， $\beta \in \left[-\frac{1}{2},1\right]$，有 $b_i\left(i\right)\ge 0$， $i=0,1,2,3$。

性质3 规范性

${\displaystyle \underset{i=0}{\overset{3}{\sum }}{b}_i\left(t\right)=1}$。

性质4 对称性

$b_i\left(1-t\right)=b_{3-i}\left(t\right),i=0,1,2,3$。

性质5 端点性质

记 $b^{\left(k\right)}\left(t\right)={\left(b_0^{\left(k\right)}\left(t\right),b_1^{\left(k\right)}\left(t\right),b_2^{\left(k\right)}\left(t\right),b_3^{\left(k\right)}\left(t\right)\right)}^{\text{T}}$，此时 $k=0,1,\text{2}$。且当 $k=0$ 时，有 $b_i^{\left(0\right)}\left(t\right)=b_i\left(t\right)$， $i=0,1,2,3$。则

$\left(b^{\left(0\right)}\left(0\right),b^{\left(1\right)}\left(0\right),b^{\left(2\right)}\left(0\right)\right)=\left(\begin{array}{ccc}\frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)& \frac{\alpha }{6}\lambda -\frac{2+\beta }{6+4\beta }\left(1-\lambda \right)& \left(-1-\frac{2}{3}\alpha \right)\lambda +\left(1-\lambda \right)\frac{1+2\beta }{3+2\beta }\\ \frac{2}{3}\lambda +\frac{2+2\beta }{3+2\beta }\left(1-\lambda \right)& 0& \left(-3-\frac{1}{3}\alpha \right)\lambda +\left(1-\lambda \right)\left(-\frac{2+4\beta }{3+2\beta }\right)\\ \frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)& -\frac{\alpha }{6}\lambda +\frac{2+\beta }{6+4\beta }\left(1-\lambda \right)& \left(3+\frac{2}{3}\alpha \right)\lambda +\left(1-\lambda \right)\frac{1+2\beta }{3+2\beta }\\ 0& 0& \left(1+\frac{1}{3}\alpha \right)\lambda \end{array}\right)$

$\left(b^{\left(0\right)}\left(1\right),b^{\left(1\right)}\left(1\right),b^{\left(2\right)}\left(1\right)\right)=\left(\begin{array}{ccc}0& 0& \left(1+\frac{1}{3}\alpha \right)\lambda \\ \frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)& -\frac{\alpha }{6}\lambda +\frac{2+\beta }{6+4\beta }\left(1-\lambda \right)& \left(3+\frac{2}{3}\alpha \right)\lambda +\left(1-\lambda \right)\frac{1+2\beta }{3+2\beta }\\ \frac{2}{3}\lambda +\frac{2+2\beta }{3+2\beta }\left(1-\lambda \right)& 0& \left(-3-\frac{1}{3}\alpha \right)\lambda +\left(1-\lambda \right)\left(-\frac{2+4\beta }{3+2\beta }\right)\\ \frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)& \frac{\alpha }{6}\lambda -\frac{2+\beta }{6+4\beta }\left(1-\lambda \right)& \left(-1-\frac{2}{3}\alpha \right)\lambda +\left(1-\lambda \right)\frac{1+2\beta }{3+2\beta }\end{array}\right)$

3. $\lambda \alpha \beta$ -T-B样条曲线的构造以及性质

定义2 给定控制点 $P_i\in R^d,d=2,3;i=0,1,2,\cdots ,n\left(n\ge 3\right)$，均匀节点向量 $U=\left[u_0,u_1,\text{}\cdots ,u_{n+4}\right]$，这里有 $u_0<u_1<\cdots <u_{n+4}$，其中参数 $\lambda \in \left[0,1\right]$， $\alpha \in \left[-4,-1\right]$， $\beta \in \left[-\frac{1}{2},1\right]$，对 $u\in \left[u_i,u_{i+1}\right],i=3,4,\cdots ,n$，能够定义一条多项式曲线段

$p_i\left(t\right)={\displaystyle \underset{j=0}{\overset{3}{\sum }}{p}_{i+j-1}{b}_j}\left(t\right),t\in \left[0,1\right]$ (2)

因此这个曲线段构成样条曲线

$p\left(u\right)=p_i\left(\frac{u-u_i}{h_i}\right),u\in \left[u_i,u_{i+1}\right]\subset \left[u_3,u_{n+1}\right]$ (3)

这里 $h_i=u_{i+1}-u_i,i=3,4,\cdots ,n$。我们定义(2)式为 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线段，(3)式为 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线。当所有的 $h_i$ 都相等时，U为等距节点向量，称对应的曲线为 $\lambda \alpha \beta \text{-}T\text{-}B$ 均匀样条曲线。

显然， $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线，当 $\lambda =1$ 的时候式(3)则退化为 $\lambda \text{-}B$ 曲线 [1]；当 $\lambda =0$ 的时候式(3)则退化为三次T-B样条曲线 [5]；当 $\lambda =1$， $\alpha =-3$ 式(3)则退化为三次均匀B样条曲线。

图2为3条 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线，当参数值不一样时，曲线形状也会随之改变。由上至下 $\left(\lambda ,\alpha ,\beta \right)$ 分别取值为 $\left(0,0,-\frac{1}{2}\right)$， $\left(1,-2.5,0\right)$， $\left(1,-3,0\right)$。

Figure 2. 3 $\lambda \alpha \beta \text{-}T\text{-}B$ -spline curves

图2. 3条 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线

由上文中的性质1~5，可以推出 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线的以下性质。

性质6 对称性

由控制点 $P_0,P_{\text{1}},P_{\text{2}},P_{\text{3}}$ 和 $P_{\text{3}},P_{\text{2}},P_{\text{1}},P_{\text{0}}$ 构成的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线是一样的，形状相同，但方向相反。

性质7 凸包性

由性质2和3可知，曲线位置在控制点生成的凸包之内。

性质8 端点性质

$\begin{array}{l}{P}_i\left(0\right)=\left[\frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)\right]\left(P_{i-1}+P_{i+1}\right)+\left[\frac{2}{3}\lambda +\frac{2+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_i\\ P_i\left(1\right)=\left[\frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)\right]\left(P_i+P_{i+3}\right)+\left[\frac{2}{3}\lambda +\frac{2+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_{i+1}\\ {P^{\prime }}_i\left(0\right)=\left[\frac{1}{6}\alpha \lambda +\left(-\frac{2+\beta }{6+4\beta }\right)\left(1-\lambda \right)\right]P_{i-1}+\left[-\frac{1}{6}\alpha \lambda +\frac{2+\beta }{6+4\beta }\left(1-\lambda \right)\right]P_{i+1}\\ {P^{\prime }}_i\left(1\right)=\left[\frac{1}{6}\alpha \lambda +\left(-\frac{2+\beta }{6+4\beta }\right)\left(1-\lambda \right)\right]P_i+\left[-\frac{1}{6}\alpha \lambda +\frac{2+\beta }{6+4\beta }\left(1-\lambda \right)\right]P_{i+2}\end{array}$

$\begin{array}{l}{P^{″}}_i\left(0\right)=\left[\left(-1-\frac{2}{3}\alpha \right)\lambda +\frac{1+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_{i-1}+\left[\left(-3-\frac{1}{3}\alpha \right)\lambda -\frac{2+4\beta }{3+2\beta }\left(1-\lambda \right)\right]P_i\\ +\left[\left(3+\frac{2}{3}\alpha \right)\lambda +\frac{1+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_{i+1}+\left(1+\frac{1}{3}\alpha \right)\lambda P_{i+2}\\ {P^{″}}_i\left(1\right)=\left[\left(-1-\frac{2}{3}\alpha \right)\lambda +\frac{1+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_{i+2}+\left[\left(-3-\frac{1}{3}\alpha \right)\lambda -\frac{2+4\beta }{3+2\beta }\left(1-\lambda \right)\right]P_{i+1}\\ +\left[\left(3+\frac{2}{3}\alpha \right)\lambda +\frac{1+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_i+\left(3+2\alpha \right)\lambda P_{i-1}\end{array}$

性质9 连续性

$\begin{array}{l}{P}_i\left(0\right)=P_{i-1}\left(1\right)\\ {P^{\prime }}_i\left(0\right)={P^{\prime }}_{i-1}\left(1\right)\\ P_i^{\left(k\right)}\left(0\right)=P_{i-1}^{\left(k\right)}(\; 1\; )\end{array}$

当 $\alpha \ne -\text{3}$ 时， $k=\text{0,1}$， $\alpha =-\text{3}$ 时， $k=\text{0,1},2$。

又因为对 $u\in \left[u_i,u_{i+1}\right],t=\frac{u-u_i}{h_i}$，有

$p^{\left(k\right)}\left(u\right)={\left(\frac{1}{h_i}\right)}^k{p}_i^{\left(k\right)}\left(t\right)$ (4)

所以，

$\begin{array}{l}{p}^{\left(k\right)}\left(u_i-\right)={\left(\frac{1}{h_{i-1}}\right)}^k{p}_{i-1}^{\left(k\right)}\left(1\right)\\ p^{\left(k\right)}\left(u_i+\right)={\left(\frac{1}{h_i}\right)}^k{p}_i^{\left(k\right)}\left(0\right)\end{array}$ (5)

由(4)和(5)式，可推出

$p^{\left(k\right)}\left(u_i+\right)={\left(\frac{h_{i-1}}{h_i}\right)}^k{p}^{\left(k\right)}\left(u_i-\right)$.

当 $\alpha \ne -\text{3}$ 时， $k=\text{0,1}$， $\alpha =-\text{3}$ 时， $k=\text{0,1},2$。

由此可说明对于 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线，当 $\alpha \ne -\text{3}$ 时 $G^1$ 连续， $\alpha =-\text{3}$ 时， $G^2$ 连续。

4. 形状参数对曲线的形状的影响

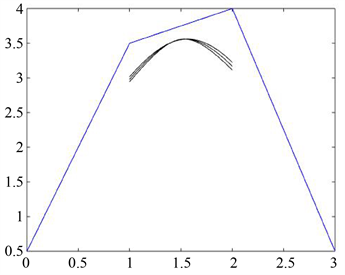
为利用构造曲线设计出满意的形状，需要明确形状参数对曲线形状的影响效果。

1) 确定参数 $\alpha ,\beta$ 值，当第三个参数 $\lambda$ 数值发生变化的时，曲线形状会随 $\lambda$ 的取值不同而不同。如图3(a)所示。此时 $\alpha =-\frac{5}{2},\beta =-\frac{1}{2}$，曲线从上至下 $\lambda$ 分别取 $\frac{\text{2}}{\text{3}},\frac{\text{1}}{\text{2}},\frac{\text{1}}{\text{3}}$。可以看出，当 $\alpha ,\beta$ 取值不变时， $\lambda$ 值越大，曲线越贴近控制多边形。

2) 确定参数 $\lambda ,\beta$，当 $\alpha$ 发生变化的时，曲线形状会随取值不同而不同。如图3(b)所示。此时 $\lambda =\frac{\text{2}}{\text{3}},\beta =-\frac{\text{1}}{\text{2}}$，曲线从上至下 $\lambda$ 分别取 $-\frac{7}{2},-3,-\frac{5}{2}$。当 $\lambda ,\beta$ 取值不变时， $\alpha$ 值越小，曲线越贴近控制多边形。

3) 确定参数 $\lambda ,\alpha$，当 $\beta$ 发生变化的时，曲线的位置以及形状就会随之发生改变。如图3(c)所示。此时 $\lambda =\frac{2}{3},\alpha =-\frac{7}{2}$，曲线从上至下 $\beta$ 分别取 $1,\frac{1}{2},-\frac{1}{2}$。当 $\lambda ,\alpha$ 取值不变时， $\beta$ 值越大，曲线越贴近控制多边形。

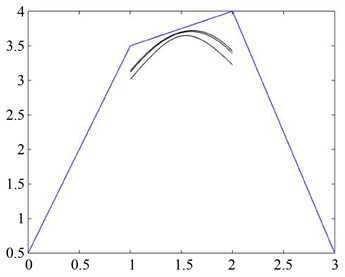
(a) $\alpha =-\frac{5}{2},\beta =-\frac{1}{2}$ 时， $\lambda =\frac{2}{3},\frac{1}{2},\frac{1}{3}$ 的情形 (b) $\lambda =\frac{\text{2}}{\text{3}},\beta =-\frac{\text{1}}{\text{2}}$ 时， $\alpha =-\frac{7}{2},-3,-\frac{5}{2}$ 的情形 (c) $\lambda =\frac{\text{2}}{\text{3}},\alpha =-\frac{\text{7}}{\text{2}}$ 时， $\beta =1,\frac{1}{2},-\frac{1}{2}$ 的情形

Figure 3. The effect of shape parameters on the curve

图3. 形状参数对曲线的影响

5. 曲线的应用

本文构造的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线既保留了有理多项式的性质，又保留了三角多项式的性质，可用来表示二次曲线。

5.1. 过首末顶点的闭曲线的设计

若 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线的控制点满足条件 $P_1=\frac{\text{1}}{\text{2}}\left(P_{\text{0}}+P_{\text{2}}\right)$， $P_{n-1}=\frac{1}{2}\left(P_{n-2}+P_n\right)$， $\lambda$ 取任意值，都有 $p\left(u_1\right)=P_1$， $p\left(u_{n-1}\right)=P_{n-1}$。所以当令 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线经过控制多边形 $P_0,P_1,\cdots ,P_n$ 的首末顶点，需增加两个控制顶点 $P_{-1}=2P_0-P_1$， $P_{n+1}=2P_n-P_{n-1}$，以 $P_{-1}{P}_0{P}_1\cdots P_n{P}_{n+1}$ 为控制定点定义曲线。

我们要求曲线封闭，则令 $P_0=P_n$，再增加两个控制点 $P_{n+1}=P_1$， $P_{n+\text{2}}=P_{\text{2}}$，以 $P_0{P}_1\cdots P_n{P}_{n+1}{P}_{n+2}$ 为控制顶点定义曲线。图4为 $\lambda =\frac{2}{3},\alpha =-\frac{7}{2},\beta =1$ 时过首末控制点的闭曲线。

Figure 4. Example of closed curve

图4. 闭曲线实例

5.2. 圆与椭圆的逼近

确定控制点 $P_0\left(-1,-1\right)$， $P_1\left(-1,1\right)$， $P_{\text{2}}\left(1,1\right)$， $P_{\text{3}}\left(1,-1\right)$， $P_{\text{4}}\left(-1,-1\right)$， $P_{\text{5}}\left(-1,1\right)$， $P_{\text{6}}\left(1,1\right)$，以 $P_0{P}_{\text{1}}{P}_{\text{2}}{P}_{\text{3}}{P}_{\text{4}}{P}_{\text{5}}{P}_{\text{6}}$ 为控制顶点的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线会更加逼近圆 $x^2+y^2={0.95}^2$，图5是 $\lambda =\frac{2}{3},\alpha =-\frac{7}{2},\beta =\frac{1}{2}$ 时，曲线对圆的逼近。

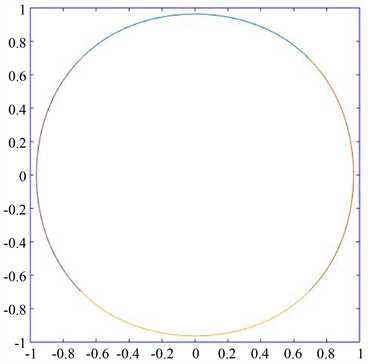
Figure 5. The approximation of the curve to the circle

图5. 曲线对圆的逼近

取定控制点 $P_0\left(-\text{3}\text{.08},-\text{2}\text{.05}\right)$， $P_1\left(-\text{3}\text{.08},\text{2}\text{.05}\right)$， $P_{\text{2}}\left(\text{3}\text{.08},\text{2}\text{.05}\right)$， $P_{\text{3}}\left(-\text{3}\text{.08},-\text{2}\text{.05}\right)$， $P_{\text{4}}\left(-\text{3}\text{.08},-\text{2}\text{.05}\right)$， $P_{\text{5}}\left(-\text{3}\text{.08},\text{2}\text{.05}\right)$， $P_{\text{6}}\left(\text{3}\text{.08},\text{2}\text{.05}\right)$，以 $P_0{P}_{\text{1}}{P}_{\text{2}}{P}_{\text{3}}{P}_{\text{4}}{P}_{\text{5}}{P}_{\text{6}}$ 为控制顶点的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线会更加逼近圆 $\frac{x^2}{\text{9}}+\frac{y^2}{\text{4}}=\text{1}$，图6是 $\lambda =\frac{4}{5},\alpha =-\frac{5}{2},\beta =-\frac{1}{2}$ 时，曲线对椭圆的逼近。

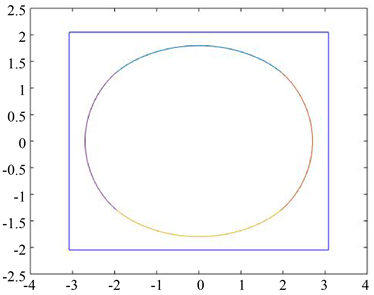
Figure 6. The approximation of the curve to the ellipse

图6. 曲线对椭圆的逼近

5.3. $\lambda \alpha \beta$ -T-B样条曲线的插值

通常情况下， $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线不过任何一个控制点。当要求 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线插值于n个数据点 $Q_1,Q_2,\cdots ,Q_n$，并插值点与分段曲线的端点相对应，由 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线的端点性质有：

$\left[\frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)\right]\left(P_{i-1}+P_{i+1}\right)+\left[\frac{2}{3}\lambda +\frac{2+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_i=Q_i$ (6)

其中 $i=1,2,\cdots ,n$，(6)式为含有 $n+2$ 个未知数，n个方程的方程组，因此应填加两个端点条件去求解唯一解。

设

$\{\begin{array}{l}{P}_{\text{1}}=Q_1\\ P_n=Q_n\end{array}$ (7)

根据式(6)与(7)，有

$\left(\frac{1}{6}\lambda +\frac{1-\lambda }{6+4\beta }\right)P_{i-1}+\left(\frac{2}{3}\lambda +\frac{2+2\beta }{3+2\beta }\left(1-\lambda \right)\right)P_i+\left(\frac{1}{6}\lambda +\frac{1-\lambda }{6+4\beta }\right)P_{i+1}=Q_i$

整理得

$P_{i-1}+\frac{12\beta +12-4\beta \lambda }{3+2\beta \lambda }{P}_i+P_{i+1}=\frac{36+24\beta }{6+4\beta \lambda }{Q}_i$

将式(6)与(7)化为等价的矩阵：

$A{E}_1=F_1$ (8)

这里

$\begin{array}{l}A={\left(\begin{array}{cccccc}\text{0}& \text{1}& \text{0}& \cdots & \text{0}& \text{0}\\ \text{1}& \phi & \text{1}& \cdots & \text{0}& \text{0}\\ \text{0}& \text{1}& \phi & \cdots & \text{0}& \text{0}\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ \text{0}& \text{0}& \text{0}& \cdots & \phi & \text{1}\\ \text{0}& \text{0}& \text{0}& \cdots & \text{1}& \text{0}\end{array}\right)}_{\left(n+2\right)\times \left(n+2\right)}\\ E_1={\left(P_0,P_1,\cdots ,P_n,P_{n+1}\right)}^{\text{T}}\\ F_1={\left(Q_1,\gamma Q_2,\gamma Q_3,\cdots ,\gamma Q_{n-1},\gamma Q_n\right)}^{\text{T}}\\ \phi =\frac{12\beta +12-4\beta \lambda }{3+2\beta \lambda }\\ \gamma =\frac{36+24\beta }{6+4\beta \gamma }\end{array}$

由(8)式可推出 $E_1=A^{-1}{F}_1$，由此，即可以求出控制顶点。

如果插值点是封闭的，则有 $Q_1=Q_n$，这样便生成一条封闭，但闭合点处不光顺的插值曲线。如果令 $P_{n-1}=P_0$， $P_n=P_{\text{1}}$， $P_{n+1}=P_{\text{2}}$，就可产生一条封闭、光顺的插值曲线。

假如插值点与分段曲线的端点对应，由性质8有：

$\left[\frac{1}{6}\lambda +\frac{1}{6+4\beta }\left(1-\lambda \right)\right]\left(P_{i-1}+P_{i+1}\right)+\left[\frac{2}{3}\lambda +\frac{2+2\beta }{3+2\beta }\left(1-\lambda \right)\right]P_i=Q_i,i=1,2,\cdots ,n$ (9)

上式为含有 $n-2$ 个未知数， $n-1$ 个方程的方程组，可求得 $n-1$ 个彼此不重复的控制顶点。把(9)式写成等价矩阵：

$B{E}_{\text{2}}=F_{\text{2}}$ (10)

其中有

$\begin{array}{l}B={\left(\begin{array}{cccccc}\text{1}& \phi & \text{1}& \cdots & \text{0}& \text{0}\\ \text{0}& \text{1}& \phi & \cdots & \text{0}& \text{0}\\ \text{0}& \text{0}& \text{1}& \cdots & \text{0}& \text{0}\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ \text{1}& \text{0}& \text{0}& \cdots & \text{1}& \phi \\ \phi & \text{1}& \text{0}& \cdots & \text{0}& \text{1}\end{array}\right)}_{\left(n-\text{1}\right)\times \left(n-\text{1}\right)}\\ E_{\text{2}}={\left(P_0,P_1,\cdots ,P_{n-3},P_{n-\text{2}}\right)}^{\text{T}}\\ F_{\text{2}}={\left(\gamma Q_{\text{1}},\gamma Q_{\text{2}},\cdots ,\gamma Q_{n-\text{2}},\gamma Q_{n-\text{1}}\right)}^{\text{T}}\\ \phi =\frac{12\beta +12-4\beta \lambda }{3+2\beta \lambda }\\ \gamma =\frac{36+24\beta }{6+4\beta \gamma }\end{array}$

由(10)式可推出 $E_2=B^{-1}{F}_2$，即可求出控制顶点。

当 $\lambda =\text{1,}\beta =\text{1}$ 以及 $\beta =\text{0},\phi =\text{4}$，此时退化为 $\lambda \text{-}B$ 曲线。

我们取 $\lambda =\frac{\text{1}}{\text{2}},\beta =\text{1}$ 时， $\phi =\frac{\text{11}}{\text{2}},\gamma =\frac{\text{15}}{\text{2}}$，此时 $Q_i=\frac{2}{15}{P}_{i-1}+\frac{11}{15}{P}_i+\frac{2}{15}{P}_{i+1}$，

$\begin{array}{l}B={\left(\begin{array}{cccccc}\text{1}& \frac{\text{11}}{\text{2}}& \text{1}& \cdots & \text{0}& \text{0}\\ \text{0}& \text{1}& \frac{\text{11}}{\text{2}}& \cdots & \text{0}& \text{0}\\ \text{0}& \text{0}& \text{1}& \cdots & \text{0}& \text{0}\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ \text{1}& \text{0}& \text{0}& \cdots & \text{1}& \frac{\text{11}}{\text{2}}\\ \frac{\text{11}}{\text{2}}& \text{1}& \text{0}& \cdots & \text{0}& \text{1}\end{array}\right)}_{\left(n-\text{1}\right)\times \left(n-\text{1}\right)}\\ E_{\text{2}}={\left(P_0,P_1,\cdots ,P_{n-3},P_{n-\text{2}}\right)}^{\text{T}}\\ F_{\text{2}}=\frac{\text{15}}{\text{2}}{\left(Q_{\text{1}},Q_{\text{2}},\cdots ,Q_{n-\text{2}},Q_{n-\text{1}}\right)}^{\text{T}}\end{array}$

给定 $F_{\text{2}}=\frac{15}{2}{\left(\left(1,1\right),\left(1,2\right),\left(2,2\right),\left(3,2\right),\left(4,5\right),\left(5,2\right)\right)}^{\text{T}}$，便可求出唯一解

$E_{\text{2}}={\left(\left(6.1160,2.4139\right),\left(0.0720,0.5092\right),\left(0.9878,2.2857\right),\left(1.9951,1.9194\right),\left(3.0391,2.1575\right),\left(3.7900,1.2143\right)\right)}^{\text{T}}$

6. 总结

本文构造了一个带三个形状参数的 $\lambda \alpha \beta \text{-}T\text{-}B$ 样条曲线，保持了三次B样条曲线的基本性质，并同时具备代数和三角多项式的优良性质，具有更好的逼近性。且能在控制顶点不需改变时，仅调节三参数，便能调整曲线形状。当给定适当的控制顶点以及形状参数时，能更加贴近圆和椭圆。最后给出了利用曲线，生成给定数据点的插值曲线的方案，并给出具体数例计算，增强了本文所构造曲线的适用性质，体现了有效性和可行性。

本文对于曲线推广到曲面的问题上没有进行讨论，为设计出更符合实际需求的造型，仍还需多加研究。