1. 引言
混沌系统的同步问题受到了广泛关注 [1] [2] [3],而混沌同步的一种统一方法是将系统表示为Lur’e系统,然后使用绝对稳定性理论研究其误差系统 [4]。Lur’e系统是由一个线性部分和一个满足扇区有界的非线性部分组成。Lur’e系统被广泛研究,它将线性项和非线性项结合起来,并成功地应用于许多动态系统 [5] [6] [7]。例如蔡氏电路、混沌系统、神经网络等。因此,混沌Lur’e系统的主从同步问题已被广泛研究,并得到了许多重要结果 [8] [9] [10]。
由于时滞普遍存在于网络控制系统 [11]、电路系统 [12]、通信系统 [13] 等各种实际系统中,时滞往往会导致系统的退化或者不稳定。在实际控制系统中,不可避免的信号传播,延迟时变时滞也无处不在。因此,很多学者对具有时滞的混沌Lur’e系统同步问题进行了研究,文献 [14] 基于新的积分不等式构造了李雅普诺夫泛函,对具有时滞的Lur’e系统的主从混沌同步进行了研究。文献 [15] 利用一组不完全正交的多项式函数,推导出一个含有更多自由矩阵的新积分不等式,结合构造的新Lyapunov-Krasovskii泛函,研究了时变时滞的混沌Lur’e系统主从同步问题。也可以看出这类系统的实际应用比较广泛。
另一方面,马尔可夫跳变系统是一类特殊的随机动态系统,在马尔可夫跳变系统中,逗留时间服从指数分布。逗留时间的概念是指两个连续跳跃之间的状态持续时间。然而,在实践中,很难保证对逗留时间分布的无记忆特征进行严格限制。在这种情况下,逗留时间服从非指数分布的基本连续随机过程通常被描述为半马尔可夫过程 [16] [17]。与马尔可夫跳变系统中的恒定的模态转移概率不同,半马尔可夫跳跃系统中的模态转移概率是时变的。马尔可夫过程是半马尔可夫随机过程的一种特殊情况。但显然,半马尔可夫跳变系统比传统的马尔可夫跳变系统有更广泛的应用领域,因为它在概率分布上的条件比较宽松。在文献 [18] 中,考虑丢包和采样周期的情况下,研究了半马尔可夫跳变混沌Lur’e系统的随机同步问题。但文献 [18] 所研究的内容时滞是常时滞,而时变时滞的存在更符合实际控制系统。因此,研究具有半马尔可夫跳跃时变时滞Lur’e混沌系统的同步分析具有重要意义。
基于上述讨论,本文研究具有半马尔可夫跳变的时变时滞混沌Lur’e系统的随机同步问题。首先,充分考虑时滞信息,利用两个零等式。然后,构造一个新的Lyapunov-Krasovskii泛函。此外,设计所需的延迟状态反馈控制器,利用线性矩阵不等式给出主系统与从系统随机同步的充分条件。最后,通过实例验证了该方法的有效性。
本文的其余部分组织如下。在第2节中,提出了要研究的问题,并介绍了在第3节中所用到的引理。在第3节中,提出了具有半马尔可夫跳变的时变时滞混沌Lur’e系统的随机同步的一般方案。第4节给出了一个仿真算例,以证明所提结果的有效性。在第5节中得出一些结论。
为了表述方便,在叙述文章之前,对如下符号说明:
表示n维欧式空间;
表示
的矩阵集;
表示矩阵X是正定(半正定)的;
表示对称矩阵中的对称项;
表示对角矩阵。
2. 预备知识
2.1. 系统描述
本文将考虑具有半马尔可夫跳变的时变时滞混沌Lur’e主从系统:
(1)
其中
是主系统,
是从系统,
是延迟状态反馈控制器,
分别是主从系统的状态向量,
是系统的输出向量,矩阵
,
,
,
,
是已知的实矩阵。
表示控制输入,
,
是待确定的反馈控制器增益矩阵。
表示时变时滞,且满足:
,
。非线性项
满足扇形条件 [14],
,其中
属于
,意味着:
(2)
是全概率空间
上右连续轨迹的半马尔可夫过程,并且在有限集合
内取值,
为时间间隔,其转移概率与转移速率的关系定义如下:
(3)
其中
表示当
时,由t时刻模态i跳跃到
时刻模态j的转移速率,
,
,同时
。
对于每一个
,
,有
,
,
,
,
。
在本文中误差信号定义为主从状态的差异
,则由(1)得误差动态系统方程如下:
(4)
其中
,令
,
,
,则由式(2)可知非线性项
在区间
上,有下列不等式成立:
(5)
这意味者:
(6)
为了简便,接下来用
来表示
。
2.2. 引理
为了得到有效结果,引入下面的引理和定义:
引理1. [19] 对一正定矩阵
,连续函数
,使得下列积分不等式成立:
(7)
定义1. [18] 对任意初始条件
,
,使得满足
(8)
则误差系统(4)是随机稳定的,从而主系统和从系统随机同步。
3. 主要结论及证明
定理1. 对给定标量
,
,若存在矩阵
,正定矩阵
,
,适当维数的矩阵
,(
可逆)使得(9)成立,
(9)
其中
,
,
,
则误差系统(4)是随机稳定的,并且求得时变时滞反馈增益矩阵
,
。
证构造如下Lyapunov泛函:
(10)
其中
,
,
则
沿系统(4)的导数计算如下:
L作为半马尔可夫过程的弱无穷小算子,则有
应用数学期望和条件概率公式可以得到:
其中h是系统从最后一次跳跃开始保持在模态i时经过的时间,
是系统从模态i到模态j的转移概率强度,由概率分布函数
的性质有:
。
记:
,
,
,
,
,
采用文献 [20] 同样的技术,化简为:
, (11)
对
求导并运用引理1可得:
, (12)
其中
。
存在正标量
由式(6)有:
,(13)
此外,由误差动态系统方程式(4)得:
, (14)
由
得:
, (15)
引入适当维数的矩阵
,(
可逆)由以上两个零等式(14)、(15)知:
, (16)
, (17)
, (18)
, (19)
将(16)~(19)四个式子相加:
,(20)
其中
,
令
,
,
由以上式(11)~(13)和式(20)相加,有:
(21)
其中
,
,
,
,
,
,
因此,根据式(9),对于任意的
,可得到
,则存在一个常数
,可以得到:
,
根据Dynkin公式,有:
,
因此,当
时有:
,
根据定理1,可得系统(4)是随机稳定的,并且控制器增益矩阵为
,
,即证明完成。
注释:由式(20)里可知,与K右乘矩阵为
或
,当
时,即与K右乘矩阵为
,则令
,同理,令
。这样便可得到满足同步控制条件的控制器增益矩阵
,
。
4. 仿真算例
在本节中,我们将通过一个例子来展示本文中提出的方法的优点和有效性。
例:考虑两种模态
的具有时变时滞的蔡氏电路如下所示:
其中
。
将该蔡氏电路用lur’e形式表示:
,
,
,
,参数
,
,
,
,
,
,
,
,
,
,
属于区间
,初值
,
。
这里有两种模态,假设半马尔可夫链的逗留时间服从每种模态的Weibull分布,具体来说,有
,其中
是Weibull分布的尺度参数,
是形状参数,注意到系统只有两种模态,对于
时,转移概率强度
,而
。特别地,当
时,用
,
的Weibull分布来表示;当
时,用
,
的Weibull分布来表示。因此,我们可以得到转移速率矩阵
,
从而进一步,推导出它的数学期望
,
取
,
,时变时滞
,利用Matlab工具箱进行对其仿真,得到控制增益矩阵:
,
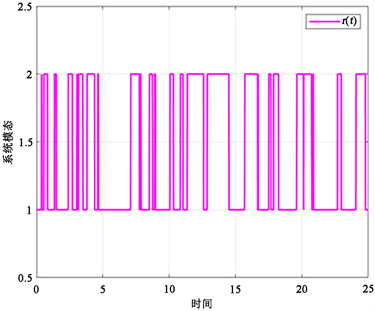
Figure 2. Switching signal with two modes
图2. 两种模态的切换信号

Figure 3. State trajectories of master system
图3. 主系统的状态轨迹

Figure 4. State trajectories of slave system
图4. 从系统的状态轨迹
由以上可知,对于上述增益矩阵,误差系统、模态、主系统和从系统的响应曲线如图所示,分别为图1~4。运用本文所提出的方法能够获得一个大范围的时滞阀值
,图1显示同步误差趋于零。因此,我们可以通过所提出的控制器使得混沌Lur’e系统的主系统和从系统达到同步。
5. 结论
针对具有半马尔可夫跳跃的时变时滞混沌Lur’e系统的随机同步问题。充分考虑时滞信息,利用零等式技术,导出了保证误差系统随机稳定性的线性矩阵不等式的充分条件,同时设计了使得主从系统同步的控制器。最后,通过一个数值算例验证了该方法的有效性。
基金项目
国家自然科学基金(12061088)。
参考文献
NOTES
*通讯作者。