基于Wolfram模型对数值相对论的研究

Research on Numerical Relativity Based on Wolfram Model

摘要: 在数值相对论研究方面，侧重于将爱因斯坦场方程转化为3 + 1维的柯西问题。在3维空间超曲面上给出初始柯西条件，随时间演化。而Wolfram模型也把爱因斯坦场方程作为先验柯西问题，在单个空间超图上指定初始柯西数据，然后通过超图重写规则进行演化，得到的因果网络结构对应时空的共形不变性结构。侧重研究Jonathan Gorard如何使用Wolfram模型提供广义相对论的数值解法，对Jonathan Gorard对Berger和Colella提出的自适应网格细化进行数值验证(包括史瓦西黑洞、克尔黑洞、史瓦西黑洞极限)。将该代码的结果和没有PDE系统的Wolfram模型演化结果进行比较，发现会在相同极限收敛，继而说明Wolfram模型的可靠性。

Abstract: In the research of numerical relativity, he focuses on transforming the Einstein field equations into the 3 + 1-dimensional Cauchy problem, and gives the initial Cauchy conditions on the 3-dimensional space hypersurface, which evolves with time. The Wolfram model takes the Einstein field equations as a priori Cauchy problem, specifies the initial Cauchy data on a single space hypergraph, and then evolves through the hypergraph rewriting rules, and the resulting causal network structure corresponds to the conformal invariant structure of space and time. This article describes how Jonathan Gorard uses the Wolfram Model to provide a numerical solution to General Relativity. Jonathan Gorard numerically validates the adaptive mesh refinement proposed by Berger and Colella (including Schwarzschild black hole, Kerr black hole, Schwarzschild black hole limit). Comparing the results of this code with the evolution of the Wolfram model without the PDE system shows that it converges at the same limit, thus illustrating the reliability of the Wolfram model.

1. 引言

众所周知，爱因斯坦场方程非常难解。目前已知的解析解依赖于时空对称性，以允许减少十个独立分量减少为个位数。且由于场方程是高度非线性的，当系统具有强相对论性时，微扰法往往会失败，即使在对称情况下，非微扰稳定性问题仍没答案。

数值广义相对论领域是Pretorius、Baker、Campanelli等通过将广义相对论转化为柯西问题，用来克服这些困难，在三维空间超曲面上指定初始柯西数值，然后向前演化(或向后)使用标准数值方法(有限微元、有限差分或有限体积等)。通过这种方法将时空上的四维爱因斯坦场方程重新表述为 $3+1$ 维含时演化，其中演化方程与相邻类空间超曲面数据相关。

而Wolfram模型是一种离散的超图变换动力学，是通过重写系统算法在超图上生成的；物理学家Jonathan Gorard在Wolfram模型中做了很多关于广义相对论和量子场论的研究。在Wolfram模型中，场方程是一个离散的柯西问题，其中柯西初始条件对应初始超图，而超图变换规则对应随时间演化的动力学。

本文主要讨论数值相对论和黑洞收敛问题，以及设计了一个双星演化系统观察Wolfram模型是否符合一个标准的物理学模型，同时探讨具有动态拓扑的CCZ4/BSSN有限差分的数值实现相比于在固定拓扑网格上传统的数值广义相对论的方案哪个具优势，并提出了关于证明电子是一个黑洞的设想。

2. 数值相对论

2.1. 具有约束阻尼的Z4

在数值相对论发展的早期，数值相对论学家在很长一段时间内，为稳定性问题头疼，无暇顾及准确性和效率问题，更谈不上考察物理问题。把场方程约化成柯西初值问题，由于收缩Bianchi恒等式，10个方程不独立。收缩比安基恒等式有4个分量，导致只有6个方程是独立的。希尔伯特正是通过这个几何考虑修正爱因斯坦提出的原始爱因斯坦方程，得到正确的希尔伯特-爱因斯坦作用量。10个未知函数，只有6个自由度是受爱因斯坦方程限制的 [1] 。

具有阻尼约束的ADM方程正是这样建立的，由于广义相对论是协变理论，故场方程的物理解是由

规范变换等价给出，其规范群的坐标变换： $y^{\mu }=f^{\mu }\left(x^v\right)$ ，由此可见，场方程 $R_{\mu \nu }=8\pi \left(T_{\mu \nu }-\frac{1}{2}T{g}_{\mu \nu }\right)$ 。一般而言不需要足够的信息来确定度量张量 $g_{\mu \nu }$ 的十个独立系数。

这里，T表示能量–动量张量的通常轨迹： $T=g_{\mu \nu }{T}^{\mu \nu }$ 。

Z4公式最初由Bona、Ledvinka、Palenzuela和Zacek引入，它是爱因斯坦场方程的扩展，因为它(真

空情况)由以下公式推导出协变拉格朗日密度： $L=\sqrt{g}{g}^{\mu \nu }\left[R_{\mu \nu }+2{\nabla }_{\mu }{Z}_{\nu }\right]$ ，Ricci曲率张量 $R_{\mu \nu }$ ：

$R_{\mu \nu }={\partial }_{\rho }{\Gamma }_{\mu \nu }^{\rho }-\partial {\left({}_{\mu }{\Gamma }_{\nu }^{\rho }\right)}_{\rho }+{\Gamma }_{\rho \sigma }^{\rho }{\Gamma }_{\mu \nu }^{\sigma }-{\Gamma }_{\sigma \mu }^{\rho }{\Gamma }_{\rho \nu }^{\sigma }$ ，度量密度 $h^{\mu \nu }=\sqrt{g}{g}^{\mu \nu }$ 。结合能量–动量第一性对 $T_{\mu \nu }$ 的贡献：

$T_{\mu \nu }+{\nabla }_{\mu }{Z}_{\nu }+{\nabla }_v{Z}_{\mu }=8\pi \left(T_{\mu \nu }-\frac{1}{2}T{g}_{\mu \nu }\right)$

Rodbeck、Frittelli、Hubner和Reula等 [2] 提出了一种具有约束的演化方程组，称为 $\lambda$ 系统。为系统补充每个约束的辅助变量 $\lambda$ ， $\lambda$ 表示约束变量的一种“时间积分”。对于场方程的四个能量–动量约束的情况，方程有一般形式的阻尼项：

$\frac{\partial \lambda }{\partial t}=a_{0}C-{\beta }_0\lambda$ , $\frac{\partial {\lambda }^i}{\partial t}=a_1{C}^i-{\beta }_0{\lambda }^i$ ,

$\frac{\partial {\lambda }_k^{ij}}{\partial t}=a_3{C}_k^{ij}-{\beta }_3{\lambda }_k^{ij}$ , $\frac{\partial {\lambda }_{kl}^{ij}}{\partial t}=a_3{C}_{kl}^{ij}-{\beta }_3{\lambda }_{kl}^{ij}$

正如Gundlach、Martín-García、Calabrese和Hinder [3] 所证明的，Z4公式的 $Z_{\mu }$ 变量可以被认为是 $\lambda$ 变量，阻尼项可通过协变引入真空场方程： $R_{\mu \nu }+{\nabla }_{\mu }{Z}_{\nu }+{\nabla }_v{Z}_{\mu }=0$ ，则方程为：

$R_{\mu \nu }+{\nabla }_{\mu }{Z}_{\nu }+{\nabla }_v{Z}_{\mu }-k_1\left[t_{\mu }{Z}_v+t_v{Z}_{\mu }-\left(1+k_2\right)g_{\mu \nu }{t}^{\sigma }{Z}_{\sigma }\right]=8\pi \left(T_{\mu \nu }-\frac{1}{2}T{g}_{\mu \nu }\right)$

假设正弦平面波的解法为： $Z_{\mu }\left(t,x^i\right)={\text{e}}^{\left(st+i{\omega }_i{x}^i\right){\hat{z}}^{\mu }}$ ，其中 ${\omega }_i$ 是实角频率，s是任意复数， ${\hat{z}}^{\mu }$ 是实幅值，此外，用 $Z_n$ 表示 $Z_i$ 在 ${\omega }_i$ 方向上的分量， $Z_A$ 表示在垂直于角频率方向上的投影，特征值：

$\left[\begin{array}{ccc}-s^2-{\omega }^2-k_1\left(2+k_2\right)s& k_{1}i\omega & 0\\ -k_1{k}_{2}i\omega & -s^2-{\omega }^2-k_1& 0\\ 0& 0& -s^2-{\omega }^2-k_1\end{array}\right]\left[\begin{array}{c}{\hat{Z}}_0\\ {\hat{Z}}_n\\ {\hat{Z}}_A\end{array}\right]=0$

$Z_A$ 产生的四个特征值s与 $k_2$ 的选择无关，即： $s=-\frac{k_1}{2}\pm \sqrt{{\left(\frac{k_1}{2}\right)}^2-{\omega }^2}$ ，对 $k_2=-1$ 时， $s=-k_1\pm i\omega$ 和 $s=\pm i\omega$ ，为无阻尼情况。

ADM线元为： $\text{d}{s}^2=-{\alpha }^2\text{d}{t}^2+{\gamma }_{ij}\left(\text{d}{x}^i+{\beta }^i\text{d}t\right)\left(x^j+{\beta }^j\text{d}t\right)$ ，得到空间度量张量 ${\gamma }_{ij}$ 的ADM方程组：

$\partial t{\gamma }_{ij}=-2\alpha K_{ij}+{\nabla }_i{\beta }_j+{\nabla }_j{\beta }_i$ ,

外曲率张量 $K_{ij}$ ：

$\partial t{K}_{ij}=\alpha \left(R_{ij}^{\left(3\right)}-2K_{ik}{K}_j^k+K_{ij}K\right)-{\nabla }_i{\nabla }_j\alpha -8\pi G\alpha \left[S_{ij}-\frac{1}{2}{\gamma }_{ij}\left(S-\tau \right)\right]+{\beta }^k{\partial }_k{K}_{ij}+K_{ik}{\partial }_j{\beta }^k+K_{kj}{\partial }_i{\beta }^k$

其中 $\tau ,S_{ij},S$ 是能量动量张量 $T_{\mu \nu }$ 的函数。外曲率张量 $K_{\mu \nu }$ 可由李导数L表示 [4] ：

$K_{\mu \nu }=-\frac{1}{2}{L}_n{\gamma }_{\mu \nu }=-{\nabla }_{\nu }^{\left(3\right)}{n}_{\mu }$ ， $L_n$ 表示沿法向量n的李导数。ADM能量约束由下式给出 [4] ：

$H=R^{\left(3\right)}-K_{ij}{K}^{ij}+K^2$

动量约束为：

$M_i={\gamma }^{il}\left({\partial }_l{K}_{ij}-{\partial }_i{K}_{jl}-{\Gamma }_{jl}^m{K}_{mi}+{\Gamma }_{ji}^m{K}_{ml}\right)$

使用Z_μ4向量的演化方程替代ADM能量、动量约束，可以强制系统为强双曲线。Z4由空间度量张量 ${\gamma }_{ij}$ 和外曲率张量 $K_{ij}$ 演化组成 [4] ：

$\left({\partial }_t-L_{\beta }\right){\gamma }_{ij}=-2\alpha K_{ij}$ ,

$\begin{array}{c}\left({\partial }_t-L_{\beta }\right)K_{ij}=-{\nabla }_i{\alpha }_j+\alpha \left[R_{ij}+{\nabla }_i{Z}_j+{\nabla }_j{Z}_i-2K_i^l{K}_{lj}+\left(K-2\Theta \right)K_{ij}-k_1\left(1+k_2\right)\Theta {\gamma }_{ij}\right]\\ -8\pi \alpha \left[S_{ij}-\frac{1}{2}\left(s-\tau \right){\gamma }_{ij}\right]\end{array}$

其中 $\Theta =n_{\mu }{Z}^{\mu }=\alpha Z^0$

2.2. 具有规范条件的保形协变Z4公式

从Z4方程的完全协变开始，对各项保形分解能够推导出Z的保形协变公式。将度量张量 ${\gamma }_{ij}$ 变换为共形空间度量张量 ${\tilde{\gamma }}_{ij}$ ： ${\tilde{\gamma }}_{ij}={\varphi }^2{\gamma }_{ij}$ ，其中 $\varphi ={\left|\begin{array}{c}\left({\gamma }_{ij}\right)\end{array}\right|}^{\frac{-1}{6}}$ 。Z4公式的共形协变表示为共形空间度量张量 ${\tilde{\gamma }}_{ij}$ 的

演化方程：

$\partial t{\tilde{\gamma }}_{ij}=-2\alpha {\tilde{A}}_{ij}+2{\tilde{\gamma }}_k\left(i,{\partial }_j\right){\beta }^k-\frac{2}{3}{\tilde{\gamma }}_{ij}{\partial }_k{\beta }^k+{\beta }^k{\partial }_k{\tilde{\gamma }}_{ij}$

其中 ${\tilde{A}}_{ij}$ 为无迹部分， ${\tilde{A}}_{ij}={\varphi }^2\left(K_{ij}-\frac{1}{3}K{\gamma }_{ij}\right)$ ，K为有迹部分， $K=K_{ij}{\gamma }^{ij}$ 。

$\begin{array}{c}\partial t{\tilde{A}}_{ij}={\varphi }^2{\left[-{\nabla }_i{\nabla }_j\alpha +\alpha \left(R_{ij}+{\nabla }_i{Z}_j+{\nabla }_j{Z}_i-8\pi S_{ij}\right)\right]}^{TF}+\alpha {\tilde{A}}_{ij}\left(K-2\text{Θ}\right)\\ -2\alpha {\tilde{A}}_{ij}{\tilde{A}}_j^l+2{\tilde{A}}_k\left(i,{\partial }_j\right){\beta }^k-\frac{2}{3}{\tilde{A}}_{ij}{\partial }_k{\beta }^k+{\beta }^k{\partial }_k{\tilde{A}}_{ij}\end{array}$

$\partial tK=-{\nabla }^i{\nabla }_i\alpha +\alpha \left(R+2{\nabla }_i{Z}^i+K^2-2\Theta K\right)+{\beta }^j{\partial }_{j}K-3\alpha k_1\left(1+k_2\right)\Theta +4\pi \alpha \left(S-3\tau \right)$

$\partial t\Theta =\frac{1}{2}\alpha \left(R+2{\nabla }_i{Z}^i-{\tilde{A}}_{ij}{\hat{A}}^{ij}+\frac{2}{3}{K}^2-2\Theta K\right)-Z^i{\partial }_i\alpha +{\beta }^k{\partial }_k\Theta -\alpha k_1\left(2+k_2\right)\Theta -8\pi \alpha \tau$

最后引入 ${\hat{\Gamma }}^i$ 的演化方程：

$\begin{array}{c}\partial t{\text{<mover accent="true"> Γ <mo> ˜ </mo> </mover>}}_{ij}=-2\alpha \left({\hat{\Gamma }}_{jk}^i-3{\hat{A}}^{jk}\frac{{\partial }_j\varphi }{\varphi }-\frac{2}{3}{\hat{\gamma }}^{ij}{\partial }_{j}K\right)+2{\hat{\gamma }}^i\left(\alpha {\partial }_k\text{Θ}-\text{Θ}{\partial }_k\alpha -\frac{2}{3}\alpha K{Z}_k\right)-2{\hat{A}}^{ij}{\partial }_j\alpha \\ +{\hat{\gamma }}^{kl}{\partial }_k{\partial }_t{\beta }^i+\frac{1}{3}{\hat{\gamma }}^{ik}{\partial }_k{\partial }_l{\beta }^l-{\hat{\Gamma }}^k{\partial }_k{\beta }^i+2k_3\left(\frac{2}{3}{\hat{\gamma }}^{ij}{Z}_j{\partial }_k{\beta }^k-{\hat{\gamma }}^{jk}{Z}_j{\partial }_k{\beta }^i\right)\\ +{\beta }^k{\partial }_k{\hat{\Gamma }}^i-2\alpha k_1{\hat{\gamma }}^{ij}{Z}_j-16\pi \alpha {\hat{\gamma }}^{ij}{S}_j\end{array}$

Jonathan Gorard推导出CCZ4的极限情况下的BSSN方程有 [4] ：

$\partial t{\hat{\Gamma }}^i=-2\left(\alpha {\partial }_j{\hat{A}}^{ij}+{\hat{A}}^{ij}{\partial }_j\alpha \right)-{\partial }_j\left(L_{\beta }{\hat{\gamma }}^{ij}\right)$

$\partial t{\tilde{\gamma }}_{ij}=-2\alpha ({\tilde{A}}_{ij}-\frac{1}{3}{\tilde{\gamma }}_{ij}\left({\tilde{A}}_{kl}{\hat{\gamma }}^{kl}\right)+2{\tilde{\gamma }}_k\left({}_i,{\partial }_i\right){\beta }^k-\frac{2}{3}{\tilde{\gamma }}_{ij}{\partial }_k{\beta }^k+{\beta }^k{\partial }_k{\tilde{\gamma }}_{ij}$

涉及黑洞的模拟，选择隧穿法处理奇点，度规被有效地分解为包含奇点的部分，以及一个保持无奇

点的部分。有： ${\gamma }_{ij}={\psi }_{BL}^4{\tilde{\gamma }}_{ij}$ 和 $K_{ij}={\psi }_{BL}^{-2}{\tilde{K}}_{ij}$ 。

能量约束简化为标量： ${\nabla }^2{\psi }_{BL}+\frac{1}{8}{\hat{K}}^{ij}{\tilde{K}}_{ij}{\psi }_{BL}^{-7}=0$ ，动量约束在外曲率上无散度： ${\nabla }_i{\hat{K}}^{ij}=0$ 。假设一个具有线性动量 $P^i$ 和角动量/自旋 $S^i$ ，由 ${\tilde{K}}_{PS}^{ij}$ 描述 [4] ：

${\tilde{K}}_{PS}^{ij}=\frac{3}{2r^2}\left(P^i{n}^j+n^j{P}^i-\left({\hat{r}}^{ij}-n^a{n}^b\right)P^k{n}_k\right)+\frac{3}{r^3}\left({ϵ}^{ikl}{S}_k{n}_l{n}^j+{ϵ}^{jkl}{S}_k{n}_l{n}^i\right)$

在距穿透距离过大处施加以下边界条件： $u-1=O\left(r^{-1}\right)$ ，和其他条件后。对于线性动量 $P^i$ 和角动量/自旋 $S^i$ 的单个黑洞的动量约束方程为 [4] ：

${\tilde{K}}_{PS}^{ij}=\frac{3}{2r^2}\left(P^i{n}^j+P^j{n}^i-\left({\hat{r}}^{ij}-n^i{n}^j\right)P^k{n}_k\right)+\frac{3}{r^3}\left({ϵ}^{ikl}{S}_k{n}_l{n}^j+{ϵ}^{jkl}{S}_k{n}_l{n}^i\right)$ ,

将结果推广到多个黑洞情况： $K^{jk}={\displaystyle {\sum }_{i=1}^N{K}_{PS\left(i\right)}^{jk}}$ ，本文研究的黑洞问题都会使用此方程。

3. 黑洞

3.1. 克尔黑洞

黑洞可分为如下几类：恒星级黑洞、中等质量黑洞、超大质量黑洞以及小黑洞(也称为微型黑洞)。恒星级黑洞的质量大约为几倍(3倍以上)到几百倍太阳质量，一般是大型恒星死亡后直接坍缩形成。中等质量黑洞大约为1千至10万个太阳质量，这种黑洞不能通过恒星演化直接形成。理论上也存在质量很小的黑洞，它们的质量接近或者远小于太阳质量。这种小质量黑洞来自于宇宙早期的密度涨落坍塌。在宇宙演化的早期，物质非常稠密，在小尺度上分布可以非常不均匀，所以密度极高的小区域中的物质可以直接塌缩成黑洞，形成所谓的“原初黑洞”。原初黑洞是当前的热门研究领域之一。原初黑洞的概念最早可以追溯到上世纪六七十年代，前苏联物理学家Y Zel’dovich和I Novikov指出早期宇宙中存在的黑洞可以通过吸积周围的福射物质而迅速增长 [5] [6] 。

考虑克尔黑洞，它的度规由下式表示 [1] ：

$\begin{array}{c}\text{d}{s}^2=\left(1-\frac{2Mr}{r^2+a^2{\cos }^2\theta }\right)\text{d}{t}^2-\frac{r^2+a^2{\cos }^2\theta }{r^2-2Mr+a^2}\text{d}{r}^2-\left(r^2+a^2{\cos }^2\theta \right)\text{d}{\theta }^2\\ -\left[\left(r^2+a^2\right){\sin }^2\theta +\frac{2Mr{a}^2{\sin }^4\theta }{r^2+a^2{\cos }^2\theta }\right]\text{d}{\varphi }^2+\frac{4aMr{\sin }^2\theta }{r^2+a^2{\cos }^2\theta }\text{d}t\text{d}\varphi \end{array}$

设 $\sin \left(\theta \right)=\sqrt{1-x^2}$ ，则 $\text{d}x=\sin \left(\theta \right)\text{d}\theta$ ， $\text{d}\theta =\frac{\text{d}x}{\sqrt{1-x^2}}$

则克尔黑洞度规公式：

$\begin{array}{c}\text{d}{s}^2=-\left(1-\frac{2Mr}{r^2+a^2{x}^2}\right)\text{d}{t}^2-\frac{4aMr\left(1-x^2\right)}{r^2+a^2{x}^2}\text{d}t\text{d}\varphi -\frac{r^2+a^2{x}^2}{r^2-2Mr+a^2}\text{d}{r}^2\\ +\left(r^2+a^2{x}^2\right)\frac{\text{d}{x}^2}{1-x^2}+\left(1-x^2\right)\left[r^2+a^2+\frac{2Mr{a}^2\left(1-x^2\right)}{r^2+a^2{x}^2}\right]\text{d}{\varphi }^2\end{array}$

将径向坐标 $\eta$ 引入Boyer-Lindquist坐标系

$r=r_{+}\cos h^2\left(\frac{\eta }{2}\right)-r_{-}\sin h^2\left(\frac{\eta }{2}\right)$ 和 $r_{+}=M\pm \sqrt{M^2-a^2}$

部分空间可以写成 $\text{d}{l}^2={\Psi }_0^4\left[{\text{e}}^{-2q_0}\left(\text{d}{\eta }^2+{\theta }^2\right)+{\sin }^2\left(\theta \right)\text{d}{\varphi }^2\right]$ ，

其中 ${\Psi }_0^4=\frac{g_{\varphi \varphi }}{{\sin }^2\left(\theta \right)}$ ， ${\Psi }_0^4{\text{e}}^{-2q_0}=g_{rr}{\left(\frac{\text{d}r}{\text{d}\eta }\right)}^2=g_{\theta \theta }$

使用Mathematic对其演化进行模拟得图1和图2：

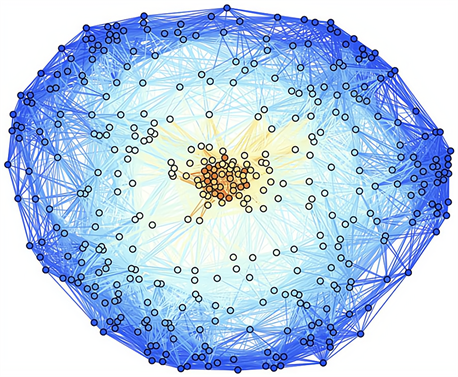
Figure 1. Kerr black hole test with a = 0.3 at time t = 20 M, 400 vertices

图1. 快速旋转的克尔黑洞在时间t = 20 M时a = 0.3，400个顶点

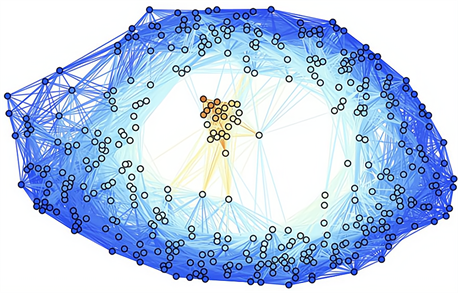
Figure 2. Kerr black hole test with a = 0.9 at time t = 20 M, 400 vertices

图2. 快速旋转的克尔黑洞在时间t = 20 M时a = 0.9，400个顶点

3.2. 史瓦西黑洞

现在考虑史瓦西黑洞，史瓦西黑洞是1916年由Schwarzschild提出的，黑洞中心为奇点。史瓦西黑

洞的度规为： $g=\text{d}{s}^2=-\left(\frac{2M}{r}\right)\text{d}{t}^2+{\left(1-\frac{2M}{r}\right)}^{-1}\text{d}{r}^2+r^2\left(\text{d}{\theta }^2+{\sin }^2\left(\theta \right)\text{d}{\varphi }^2\right)$ 。

使用 $u^2=r-2M$ 代替史瓦西径向坐标r以wormhole度规形式表示，则：

$g=\text{d}{s}^2=-\frac{u^2}{u^2+2M}\text{d}{t}^2+4\left(u^2+2M\right)\text{d}{u}^2+u^2\left(\text{d}{\theta }^2+{\sin }^2\left(\theta \right)\text{d}{\varphi }^2\right)$ .

它描述了一个有两个薄片的时空，即 $u>0$ 和 $u<0$ ，由 $r=2M$ 和 $u=0$ 连接，度规g沿着它消失。保形因子 $\psi$ 表达式为： $\psi ={\left(\frac{M}{2r}\right)}^{-2}$ ，黎曼曲率张量 $R_{ijkl}$ 四个非零的分量不变。使用Schwarzschild保形因子作为细化算法 $\phi =\psi$ 的标量场，边界条件为 [4] ：

$\frac{\partial f\left(x,t\right)}{\partial t}=-\frac{v{x}_i}{r}\frac{\partial f\left(x_i,t\right)}{\partial x_i}-v\frac{f\left(x_i,t\right)-f_0\left(x_i,t\right)}{r}$

对于任意标量场f，离场域中心径向距离 $r=\sqrt{x^2+y^2+z^2}$ ，空间边界值为 $f_0$ ，辐射速度 $v=1$ 。

Mathematic的模型演化结果如图3：

Figure 3. Hypergraph of a Schwarzschild black hole at time t = 0 M, 800 vertices

图3. 史瓦西黑洞在时间t = 0M，800个顶点时的超图

3.3. 史瓦西黑洞的收敛

对于演化于两个等质量史瓦西黑洞正面碰撞的二元黑洞，Jonathan Gorard给出其度规和极限 [4] ：

$g=\text{d}{s}^2={\Phi }^4\text{d}{s}_f^2$

式中 $\text{d}{s}_f^2$ 表平面空间的线元， $\Phi$ 是拉普拉斯方程的解， ${\nabla }^2\Phi =0$ 。

$\text{d}{s}^2={\Phi }^4\left(R,\theta ,{\mu }_0\right)\left(\text{d}{R}^2+R^2\left[\text{d}{\theta }^2+{\sin }^2\left(\theta \right)\text{d}{\varphi }^2\right]\right)$

$\text{d}{s}_f^2$ 描述了平面三维空间球坐标， $\left(R,\theta ,\varphi \right)$ ，拉普拉斯解 ${\Phi }_{BL}L\left(R,\theta \right)$ 采用牛顿引力势表示 [4] ：

${\Phi }_{BL}L\left(R,\theta \right)=1+\frac{1}{2}\left(\frac{m}{\sqrt{r^2{\sin }^2\left(\theta \right)+{\left(R\cos \left(\theta \right)-z_0\right)}^2}}+\frac{m}{\sqrt{r^2{\sin }^2\left(\theta \right)+{\left(R\cos \left(\theta \right)+z_0\right)}^2}}\right)$

令 $M=2m$ ，分母中平方根项可以展成幂级数：

$\text{d}{s}_{BL}^2-{\left[1+\frac{M}{2R}\underset{l=0,2,4,\cdots }{{\displaystyle \sum }}{\left(\frac{z_0}{R}\right)}^l{P}_l\left(\cos \left(\theta \right)\right)\right]}^4\left(\text{d}{R}^2+R^2\left[\text{d}{\theta }^2+{\sin }^2\left(\theta \right)\text{d}{\varphi }^2\right]\right)$

$P_l$ 表勒让德多项式， ${\displaystyle {\sum }_{l=0}^{\infty }{P}_l\left(x\right)t^n}=\frac{1}{\sqrt{1-2xt+t^2}}$

将各向同性径向坐标R转换为Schwarzschild径向坐标r，即： $R=\frac{{\left(\sqrt{r}+\sqrt{r-2M}\right)}^2}{4}$ ，利用微扰处理

参数来描述非球面几何：

$\text{d}{s}_{BL}^2\approx \left[1+\frac{\frac{2M}{R}}{1+\frac{M}{2R}}\underset{l=2,4,6,\cdots }{{\displaystyle \sum }}{\left(\frac{z_0}{M}\right)}^l{\left(\frac{M}{R}\right)}^l{P}_l\left(\cos \left(\theta \right)\right)\right]\left(\frac{\text{d}{r}^2}{1-\frac{2M}{r}}+r^2\left[\text{d}{\theta }^2+{\sin }^2\left(\theta \right)\text{d}{\varphi }^2\right]\right)$

有双星黑洞形式的初始数据后，Schwarzschild黑洞的质量均为0.5 M，初始间隔为1 M，双星的质心位于在计算域中，为了计算简便设置了边界条件。Mathematic的模拟结果如图4所示：

Figure 4. The spatial hypergraph represents the z-axis projection of the variation of the Schwarzschild black hole convergence test hypersurface along the time t = 0 M, with the vertex at 800

图4. 空间超图表示沿时间t = 0 M时施瓦西黑洞收敛测试超曲面变化的z轴投影，顶点为800

4. Wolfram模型的演化

空间超图 $H=\left(V,E\right)$ ，它是有限且无向的，Wolfram模型可以理解为一个集合变换系统，如图5所示。虽然没有应用重写规则的顺序，但从可能的匹配不重叠子超图，仍然可获得确定的演化。

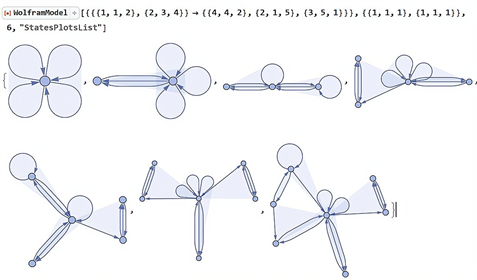
Figure 5. Transformed hypergraph of wm3328

图5. wm3328的变换规则

在模型中一切演化都由超图表示，状态通过事件联系起来。事件是如何联系起来的呢？要看两个事件是否有因果关系。一个事件是否依赖于另一个事件就是说它的全部(或部分)输入来自另一个事件的输出。超图的演化可构造一个因果图，更新的事件对应节点，有向边表示这些事件之间的因果关系。

与超图同之处在于，因果图必须考虑其边界有向性(极限)。系统演化中的连续步骤对应于通过该因果图的连续切片。在因果不变的情况下，任何可能的更新顺序都必须对应于图的可能的因果关系。

在一些黎曼流形 $\left(M,g\right)$ 中选择围绕点 $p\in M$ 的测地线法线坐标系开始。如果 $\left(M,g\right)$ 是一个 $C^{\infty }$ 流形，对于任何点 $x\in M$ ，有一个线性映射： $D:C^{\infty }\left(M\right)\to R$ ，且满足莱布尼茨恒等式。

标量场 $\varphi$ 在因果图中的所有事件中都恒定，因此对于顶点u和v的耦合常数满足 $\left(u,v\right)=1$ ，并用泊松分布代替因果图动力学的弱重写事件，Wolfram模型系统构建的离散Einstein-Hilbert作用量简化为

Benincasa-Dowker作用量的一般d维形式 [4] ： $S^{\left(4\right)}\left(C\right)={\displaystyle {\sum }_{e\in C}R(\; e\; )}$

在 $d=4$ (3 + 1维)的情况下，可以根据事件 $e\in C$ 的因果历史中k最近邻集的基数描述：

$N_k\left(e\right)=\left|\begin{array}{c}{L}_k\left(e\right)\end{array}\right|=\left|\begin{array}{c}\left\{e^{\prime }\prec ee:n\left[e,e^{\prime }\right]=k\right\}\end{array}\right|$

$d^{\prime }$ 显式形式：

$S^{\left(4\right)}\left(C\right)=\frac{4}{\sqrt{6}}\left[n-n_0\left(C\right)+9N_1\left(C\right)+16N_2\left(C\right)+8N_3\left(C\right)\right]$ .

其中 $N_k\left(C\right)$ 表示C中包含k个元素的离散时空区间的数量，n表示事件集 $n=\left|C\right|$ 的基数。根据Cunningham [7] 的证明，假设零表面项对积分的贡献来自光锥的更下方外消失在极限，则离散作用量 $S^{\left(4\right)}$ 的期望值将收敛到 ${\rho }_c\to \infty$ 的连续流形 $\left(M,g\right)$ 上的作用量 $S_{EH}\left(g\right)$ ：

$\underset{{\rho }_c\to \infty }{{\displaystyle \sum }}\left[\hslash \frac{l^2}{l_p^2}\langle {\tilde{S}}^2\left(C\right)\rangle \right]=S_{EH}(\; g\; )$

其中 $\hslash$ 表示缩减的普朗克常数， $l_p$ 表示普朗克长度。

可以从超图或因果图中得到曲率，可以通过Einstein-Hilbert作用量给定Wolfram模型一个在连续极限中满足爱因斯坦场方程演化的规则，通过构造一个超图H。

这可以给定相对论柯西问题的初始条件，使用泊松分布构造 $\Phi \left(H\right)$ 的元素，其中H的n个顶点在体积为v的空间内给出： $P_v\left(n\right)=\frac{\left(P_{c}v\right)n}{n!}{\text{e}}^{-P_{c}v}$ ，在空间区域内的顶点数的期望值为： $\langle \hat{n}\rangle =P_{c}v$ 。

为一对静态Schwarzschild黑洞建立Brill-Lindquist双星黑洞初始数据，每个黑洞的质量为0.5 M，初始间隔为1 M，使得双星的质心位于初始超图的中心，如图6。

Figure 6. Spatial hypergraph of the initial hypersurface configuration for the Schwarzschild frontal collision test at time t = 24 M, with 800 vertices

图6. 时间t = 24 M时史瓦西黑洞正面碰撞测试的初始超曲面配置的空间超图，顶点为800

使用相同方法确定克尔黑洞如图7：

Figure 7. Configuration of the head on collision of rapidly rotating Kerr black holes test with a = 0.6 at time t = 24 M

图7. 在时间t = 24 M时a = 0.6的快速旋转的克尔黑洞

5. 结论

科学必须保持怀疑态度，在这个世界上没有什么是完全确定的。如果我们有一个特定的模型，具有一组特定的基本规则和初始条件，我们可能会认为我们一定能得到它的所有信息。但所有的模型都不可避免的出现了计算不可约性，不能期望缩短计算工作以找出它的本质。

可我们的宇宙中仍有许多方面是特定于特定的基本规则的。比如说空间的维度、粒子的特定质量。可我们目前仍不知道找到这些特定规则计算不可约性的大小。本文中提到的参数会对基础规则施加强大的约束，而且规则很简单，可以唯一确定。为了以满足连续极限中的爱因斯坦场方程，超图的变换被设置成了已知的规则。进行了类似的收敛和稳定性分析，发现它确实收敛到等效的极限。

本文是对该领域的初步探究，对于Wolfram模型的演化过程，设计了一个史瓦西黑洞和克尔黑洞的双星黑洞演化系统，给出了计算极限的公式并对模型进行验证，发现Wolfram模型和Jonathan Gorard对Berger和Colella提出的PDE系统演化结果一致，可认为Wolfram模型与数值相对论的结果一致。通过模拟发现，动态拓扑的CCZ4/BSSN有限差分的数值实现相比于在固定拓扑网格上传统的数值广义相对论的方案更具有优势。

这里提出一个假设，随着能量密度的增加，能量、时空和量子信息变得更加不确定。当测量距离黑洞足够远时，这种不确定性可以忽略不计。将这种不确定性称为Koide-Lestone不确定性，并且Lestone认为电子是一个非常小的类似黑洞的物。Koide-Lestone不确定性可根据Wolfram的有向超图理论来定义，这说明Wolfram模型可以用来证明Lestone的电子黑洞理论。

但目前Choptuik发现了一种关于临界点精确数值并可用于推导超临界关系的相对论临界方法。在具有高斯状态的弯曲时空中构建了一个完全非相互作用的量子场论。或许将来Wolfram团队还会对霍金辐射、时空纠缠熵，甚至可能是ER=EPR假设等现象进行数值研究。

参考文献