氢原子动态极化率和Tune-Out波长的理论计算

Theoretical Calculations of the Dynamic Polarizabilites and the Tune-Out Wave Length for H Atom

摘要: 本文给出了稳定变分方法计算单价原子的动态极化率的理论方法，在此基础上，自主开发了计算程序。利用该程序，以氢原子为例，计算了不同频率下氢原子基态的动态极化率。本文计算结果与文献中Green函数法的结果进行了比较，具有很好的一致性。分析了稳定变分法的收敛性，并利用计算的动态极化率进一步确定了相应的tune-out波长。

Abstract: The theoretical method for calculating the dynamic polarizability of monovalent atoms by the variationally stable procedure is given. On this basis, the calculation program is independently developed by us. As an application, the dynamic polarizabilities at different frequencies are calculated with hydrogen atoms as an example, by this program. The calculation results are compared with the Green function data in the literature, with good consistency. The convergence of the variationally stable procedure is analyzed, and the corresponding tune-out wavelength is further determined by using the polarizability calculated in the present work.

1. 引言

极化率是描述原子在外电场作用下核外电子云偏离正常分布的一个物理量，在宇称不守恒、原子光钟、钟跃迁中的黑体辐射位移以及原子相互作用的色散系数等方面有着极其重要的应用。当原子态在特定激光的波长下，电子云不受外电场影响，这一特征波长称为tune-out波长 [1]。人们在该波长的激光场下进行实验测量，可以避免电场的影响，从而得到高精度的原子参数。理论上计通过计算原子的动态极化率，可以确定原子的tune-out波长，为实验测量提供数据支持。

价壳层只有一个电子的原子(离子)动态极化率一直是人们关注的热点 [2] [3]。这是由于这类原子价壳层上只有一个电子，其极化率的精确计算可以用来验证相对论和量子电动力学理论，检验新的计算方法的正确性和可靠性等，并在此基础上给出精确的原子数据。Baye [4] 利用Lagrange网格方法给出了非相对论下氢原子静态极化率的解析表达式，该方法可以提供精确的能量和波函数。Sahoo等人 [5] 利用对动态极化率的研究，确定了圆极化光诱导Li、Na和K碱金属原子ns-np跃迁的魔幻波长。指出可以利用圆极化光实现对碱金属原子的不同原子态的俘获。1986年，Tang和Chan [6] 利用径向库仑Green函数法给出了氢原子任意原子态的多极动态极化率；2014年，唐永波等人 [7] 在相对论框架下发展了半经验原子结构模型方法，利用B样条计算了碱金属原子的极化率，由极化率给出了长程两体色散系数。除了自由状态下的原子离子极化率计算，约束环境下类氢离子极化率计算也是人们感兴趣的课题。如2021年，Mukherjee等人 [8] 分别利用ECSCP和WCP势函数描述了稠密等离子体和弱耦合等离子体环境，计算了这两类等离子体约束下的类氢离子的动态极化率，并与自由环境下极化率进行了比较；同年，He等人 [9] 利用态求和方法计算了Hulthúen势下类氢原子多极极化率，其中系统的束缚态和准连续态波函数由广义赝光谱方法产生。近年，黄时中等人 [10] 采用稳定变分法计算了碱金属等电子系列两体、三体色散系数。计算结果可以与数值计算方法的结果相比较，均具有很好的一致性。稳定变分方法最早由Gao和Starac提出 [11] [12]，由于该方法有两个显著优势：第一，随着所选的基组数目的增加，极化率和色散系数的计算结果迅速收敛并趋于稳定；第二，此方法的应用只需要知道原子的基态波函数。近年来，稳定变分法被广泛用来计算基态氢原子和基态碱金属原子的极化率及色散系数 [13] [14]。虽然，针对动态极化率已经开展了大量的计算工作，但是随着冷原子物理和原子钟的研究进展，对原子动态极化率理论数据的需要越来越大。因此，从理论探讨动态极化率的计算方法，并给出大量高精度的极化率数据是十分必要的。

本文将基于稳定变分法，给出单价原子动态极化率计算的理论方法，编写相应的计算程序代码。以氢原子为例，计算了其动态极化率，并确定存在的tune-out波长，这些计算给出新的计算数据，可以为后来的研究者提供一个很好的参考。

2. 理论方法

2.1. 哈密顿和波函数

类氢体系是少数几个可以被精确求解的量子体系之一。在原子单位之下，类氢体系的哈密顿可以写成为

$\hat{H}=-\frac{{\nabla }^2}{2}-\frac{Z}{r}=-\frac{1}{2r}\frac{d^2}{d{r}^2}r-\frac{Z}{r}+\frac{l^2}{2r^2}$ (1)

上式第一个等号后面的第一项是电子的动能，第二项电子和原子核的库仑排斥势。第二个等式是在球坐标系下表示。Z为核电荷数。(1)式对应的本征值和本征函数分别为

$E_n=-\frac{Z^2}{2n^2}$ (2)

和

${\psi }_{nlm}\left(r,\theta ,\phi \right)=R_{nl}\left(r\right)Y_{lm}\left(\theta ,\phi \right)$ (3)

式中n，l和m分别为主量子数、轨道量子数和磁量子数。 $Y_{lm}\left(\theta ,\phi \right)$ 是球谐函数，是电子波函数的角向部分， $R_{nl}\left(r\right)$ 是电子波函数的径向部分，可以表示为

$R_{nl}\left(r\right)=N_{nl}{\left(\frac{2Zr}{n}\right)}^l{e}^{\frac{Zr}{n}}{\displaystyle \underset{k=0}{\overset{n-l-1}{\sum }}\frac{\left(n+l\right)!}{\left(n-l-1-k\right)!\left(2l+1+k\right)!k!}}{\left(-\frac{2Zr}{n}\right)}^k$ (4)

式中 $N_{nl}$ 为归一化因子，可以写成

$N_{nl}={\left(\frac{2Z}{n}\right)}^{3/2}\sqrt{\frac{\left(n-l-1\right)!}{\left(n+l\right)!2n}}$ (5)

2.2. 动态极化率

多极动态极化率可以用双光子过程的跃迁矩阵 $T_{i\to i}^{\left(2\right)}\left(\omega \right)$ 表示，即 [11] [12]

${\alpha }_L\left(\omega \right)=-\left[T_{i\to i}^{\left(N=2\right)}\left(\omega \right)＋T_{i\to i}^{\left(N=2\right)}\left(-\omega \right)\right]$ (6)

其中跃迁矩阵元的定义为

$T_{i\to i}^{\left(2\right)}\left(\omega \right)=\langle i\left|{\hat{d}}_L\frac{1}{E_i+\omega -\hat{H}}{\hat{d}}_L\right|i\rangle$ (7)

这里 $|i\rangle \equiv {\psi }_{nlm}\left(r,\theta ,\phi \right)$ 是原子的初态波函数， $E_i$ 是原子的初态能量， $\hat{H}$ 是原子的哈密顿量， $\omega$ 是多极场的频率， ${\hat{d}}_L$ 是 $2^L$ 极矩算符，

${\hat{d}}_L=\sqrt{\frac{4\pi }{2L+1}}{r}^L{Y}_{L0}\left(\theta ,\varphi \right)$ (8)

当 $\omega \to 0$ 时，即得到静态极化率。

为了计算双光子过程的跃迁矩阵元，按照稳定变分法，引入中间态 $|\lambda \rangle$，即

$|\lambda \rangle =\frac{1}{E_i+\omega -\hat{H}}{\hat{d}}_L|i\rangle$ (9)

从而，(7)式可以改写成

$T_{i\to i}^{\left(2\right)}\left(\omega \right)=2\langle i\left|{\hat{d}}_L\right|\lambda \rangle -\langle \lambda \left|E_i+\omega -\hat{H}\right|\lambda \rangle$ (10)

将中间态 $|\lambda \rangle$ 用斯莱特基进行展开，则有

$|\lambda \rangle =Y_{l\text{'}m\text{'}}\left(\theta ,\phi \right){\displaystyle \underset{\mu =1}{\overset{M}{\sum }}{a}_{\mu }{\varphi }_{\mu }\left(r\right)}$ (11)

其中，斯莱特波函数 ${\varphi }_{\mu }\left(r\right)$ 形式为

${\varphi }_{\mu }\left(r\right)=N_{\mu }{r}^{l\text{'}+\mu }{\text{e}}^{-r}$ (12)

式中的 $N_{\mu }$ 是归一化因子

$N_{\mu }=\sqrt{\frac{2^{2\mu +2l^{\prime }+3}}{\left(2\mu +2l^{\prime }+2\right)!}}$ (13)

(11)式中 $a_{\mu }$ 是展开系数，M是基组的大小。将初态和中间态代入到(10)式，完成的积分，可得

$T_{i\to i}^{\left(2\right)}\left(\omega \right)=2{\displaystyle \underset{\mu }{\sum }{a}_{\mu }{N}_{\mu }{D}_{\mu }}-{\displaystyle \underset{\mu }{\sum }{\displaystyle \underset{{\mu }^{\prime }}{\sum }{a}_{\mu }}{a}_{{\mu }^{\prime }}{N}_{\mu }{N}_{{\mu }^{\prime }}}\left(A_{\mu {\mu }^{\prime }}+B_{\mu {\mu }^{\prime }}+C_{\mu {\mu }^{\prime }}\right)$ (14)

根据变分原理 $\frac{\partial T_{i\to i}^{\left(2\right)}\left(\omega \right)}{\partial a_u}=0$，得到参数 $a_{\mu }$ 所满足的代数方程

${\displaystyle \underset{\mu =1}{\overset{M}{\sum }}{a}_{\mu }}{N}_{\mu }{N}_{\mu }\left(A_{\mu {\mu }^{\prime }}+B_{\mu {\mu }^{\prime }}+C_{\mu {\mu }^{\prime }}\right)=N_{{\mu }^{\prime }}{D}_{{\mu }^{\prime }}$ (15)

上式是一个M×M维线性方程组，通过求解这个方程组，可以确定系数 $a_{\mu }$，然后将其代入式(14)式可以求得氢原子的多极动态极化率。上式中 $D_{\mu }$ 的具体形式为

$D_{\mu }={\epsilon }^l\left(n+l\right)!I\left(lmL0l^{\prime }{m}^{\prime }\right){\displaystyle \underset{k=0}{\overset{n-l-1}{\sum }}\frac{{\left(-\epsilon \right)}^k\left(k+\mu +\beta \right)!}{\left(n-l-1-k\right)!\left(2l+1+k\right)!k!{\left(1+\epsilon \right)}^{k+\mu +\beta +1}}}$ (16)

其中 $\beta =L+l+l^{\prime }+1$， $\epsilon =2Z/n$。 $I\left(lmL0l^{\prime }{m}^{\prime }\right)$ 为角向积分部分，可以用3-J符号表示

$I\left(lmL0l^{\prime }{m}^{\prime }\right)={\left(-1\right)}^m\sqrt{\left(2l+1\right)\left(2l^{\prime }+1\right)}\left(\begin{array}{ccc}l& L& l^{\prime }\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}l& L& l^{\prime }\\ -m& 0& m^{\prime }\end{array}\right)$ (17)

其余几个积分参数分别表示为

$\begin{array}{l}{A}_{\mu {\mu }^{\prime }}=\left(E_i+\omega +\frac{1}{2}\right)\frac{\bar{\mu }！}{2^{\bar{\mu }+1}}\\ B_{\mu {\mu }^{\prime }}=\left(\mu +l+1\right)\frac{\left(\bar{\mu }-1\right)！}{2^{\bar{\mu }}}\\ C_{\mu {\mu }^{\prime }}=\frac{\left(\mu -1\right)\left(\mu +2l\right)}{2}\frac{\left(\bar{\mu }-2\right)!}{2^{\bar{\mu }-1}}\end{array}$ (18)

其中 $\bar{\mu }=2l+{\mu }^{\prime }+\mu$。

3. 计算与讨论

基于以上计算公式，我们编写了相应的计算代码，并以氢原子为例，计算了基态的动态极化率，结果在表1中给出。

Table 1. Theoretical calculation of the dynamic polarizabilities of H atom

表1. 氢原子动态极化率的理论计算

为了考查本文计算的收敛性，表1中分别给出了M = 1，M = 5，M = 10和M = 15的计算结果。可以看出，ω较小时，收敛的较快，ω越大收敛的越慢。在本文所考虑的范围内，M = 15已经足够收敛。为了保证本文计算方法和程序代码的可靠性，我们将M = 15的计算结果与径向库仑Green函数法 [4] 的计算结果进行了比较。从表中可以看出，本文的计算结果与文献的结果符合的很好，除了ω = 0.444和ω = 0.445时误差分别为2.16%和2.18%外，其余误差均在1%以内。

从表1中的数据我们还可以看到，动态极化率随着ω的变化而发生波动。为了清晰地展现这种依赖关系，我们在图1中给出了动态极化率与ω变化曲线。可以看出，在ω = 0.3~0.65范围内，动态极化率存在若干ω = 0位置，这些位置对应的波长即tune-out波长，tune-out波长对于精密的实验测量非常重要。因为该波长光入射下，原子的电子云分布不受外场影响，这就为原子数据的精确测量提供了保证。图中红色原点标出的即tune-out波长的位置，对应的分别为0.43，0.46，0.49，0.53和0.59。

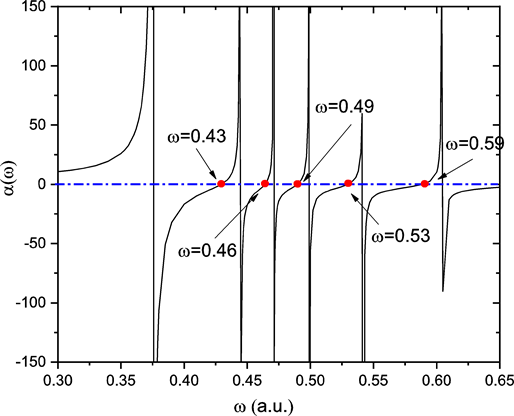
Figure 1. Dynamic polarizabilities and tune-out wavelength of H atom in ground state

图1. 氢原子基态动态极化率及tune-out波长

4. 总结

本文给出了稳定变分法计算动态极化率的理论计算公式，编写了相应的计算程序。利用我们的程序，以氢原子为例，计算了氢原子基态的动态极化率，考察了基组大小对计算结果的影响，发现对于氢原子动态极化率，M = 15计算结果已经足够收敛。计算结果与文献比较，具有很好的一致性，说明本文的计算方法和计算代码的可靠性。利用我们计算的动态极化率，给出了五个tune-out波长。本文的结果可以为原子参数的精密实验测量提供数据支撑。需要说明的是，与其他数值计算相比，本文所采用的稳定变分方法是完全解析的，再结合最弱受约束电子势模型理论 [15] 给出得任意原子的波函数，理论上可以完成任意单价电子的原子体系任意原子态的动态极化率计算。由于是解析计算，物理图像更加清晰，程序编写简单，易于推广。

基金项目

大学生创新创业项目(S202110375080)资助课题。