具有避难所的不连续食饵–捕食者模型的动力学研究

Dynamics Research of a Discontinuous Predator-Prey Model with Shelter

摘要: 本文研究了一类基于避难所控制策略的不连续食饵–捕食者模型的全局动力学。利用Filippov理论和非光滑分析方法得到了实平衡点和伪平衡点的存在性，并证明了这些平衡点的全局渐近稳定性。借助数值模拟，分析了所得结果的生物学意义。

Abstract: In this paper, the global dynamics of a discontinuous predator-prey model based on shelter control strategy is studied. By using Filippov theory and non-smooth analysis method, the existence of real equilibrium and pseudo equilibrium is obtained, and the global asymptotic stability of these equi-libria is proved. With the help of numerical simulation, the biological significance of the obtained results is analyzed.

1. 引言

近年来，食饵–捕食者系统的研究一直是数学和生态学研究的重要课题和热点问题之一 [1]。建立食饵–捕食者模型也是研究生态动力学的一个常用的并且很重要的研究方法。Gause等人在1936年所做的关于草履虫和酵母细胞的实验，通过实验数据可以得到两个物种之间的相互作用依赖于酵母细胞的浓度 [2]。随后Gause等人利用不连续的饱和函数替换Lotka-Volterra食饵–捕食者模型中的线性消耗率，并将改进后的模型称为Gause模型，之后在 [3] 中作者利用Filippov理论重新分析了该模型，并提出Gause模型可能是第一个描述猎物避难所使用效果的右端不连续食饵–捕食者模型。此后有关食饵避难的食饵–捕食者系统引起了国内外学者的广泛关注。黄等人在 [4] 中所介绍的不连续微分方程理论对食饵–捕食者模型的研究有重要的作用。唐等人 [5] 也对不连续食饵–捕食者模型进行了全局稳定性分析。王和李等人在 [6] 中给出了更具有一般性的模型。在经典捕食食饵模型的基础上， [7] 基于比例控制的阈值策略，比较系统地研究了一类带有食饵避难的型捕食者–食饵模型，虽然可以得到比较好的结果，但是比例控制的策略不太容易实现。而在本文中，根据食饵数量的多少来决定是否采取措施，当食饵的数量少于给定的阈值的时候加入避难所，从而来保护食饵，避免其灭绝，当食饵的数量高于阈值的时候，捕食者以第一类功能函数来消耗猎物 [8]，从而保证大自然的生态多样性。

2. 模型介绍及预备知识

考虑如下具有避难所的不连续食饵–捕食者模型。

$\{\begin{array}{l}\frac{\text{d}u}{\text{d}s}=au\left(1-\frac{u}{k}\right)-c\varphi \left(u\right)v\\ \frac{\text{d}v}{\text{d}s}=-dv+b\varphi \left(u\right)v\end{array}$ (2.1)

其中u和v分别表示s时刻的食饵和捕食者的数量；a表示食饵的内在增长率；k表示最大的环境容纳量；c表示捕食者的捕获速率；d表示捕食者的死亡率；b表示捕食者的转化速率，b < c，

$\phi \left(u\right)=\{\begin{array}{l}0,u<\omega ,\\ mu,u>\omega .\end{array}$

为控制函数， $\omega >0$ 为控制阈值。为了减少模型(2.1)中独立参数的个数，对该模型进行无量纲化及时

间尺度变换。令 $u=kx,v=ky,s=\frac{1}{a}t$ 得到

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\alpha \varphi \left(x\right)y\\ \frac{\text{d}y}{\text{d}t}=-\gamma y+\beta \varphi \left(x\right)y\end{array}$ (2.2)

其中 $\alpha =\frac{c}{a},\gamma =\frac{d}{a},\beta =\frac{b}{a}$，控制函数变为

$\varphi \left(u\right)=\{\begin{array}{l}0,x<\theta ,\\ ax,x>\theta .\end{array}$

记 $R_{+}^2=\left\{\left(x,y\right)|x\ge 0,y\ge 0\right\}$。显然，(2.2)由下面两个子系统

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)\\ \frac{\text{d}y}{\text{d}t}=-\gamma y\end{array}\left(x,y\right)\in G_1$ (2.3)

和

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-a\alpha xy\\ \frac{\text{d}y}{\text{d}t}=-\gamma y+a\beta xy\end{array}\left(x,y\right)\in G_2$ (2.4)

构成，分别称为左子系统和右子系统，其中

$G_1=\left\{\left(x,y\right)\in R_{+}^2|x<\theta \right\},G_2=\left\{\left(x,y\right)\in R_{+}^2|x>\theta \right\}.$

记

$\sum =\left\{\left(x,y\right)\in R_{+}^2:x=\theta \right\}.$

称 $\sum$ 为系统(2.2)的切换线。

对于左子系统(2.3)，存在平衡点 $E_1^0=\left(0,0\right),E_1^1=\left(1,0\right)$。对于右子系统(2.4)，存在平衡点 $E_2^0=\left(0,0\right),E_2^1=\left(1,0\right)$ 且当 $\alpha \beta >\gamma$ 时存在内部平衡点

$E_1=\left(x_1,y_1\right)=\left(\frac{\gamma }{a\beta },\frac{a\beta -\gamma }{a^2\alpha \beta }\right).$

关于子系统的动力学性质，我们有下面的结果，其证明结果可参考文献 [7]。

命题2.1 对于子系统(2.4)，当 $\alpha \beta <\gamma$ 时 $E_2^1$ 是全局渐近稳定的，而当 $\alpha \beta >\gamma$ 时 $E_1$ 是全局渐近稳定的。

由于系统(2.2)的向量场是不连续的，本文将讨论系统(2.2) Filippov意义下的解，其定义如下。

定义2.2 若向量函数 $\left(x\left(t;x_0,y_0\right),y\left(t;x_0,y_0\right)\right)$ 在 $\left[0,T\right)$ 的任意有界闭子区间 $\left[t_1,t_2\right]$ 上绝对连续 $\left(0<T\le +\infty \right)$，满足 $x\left(0\right)=x_0$ 和 $y\left(0\right)=y_0$，并且存在可测函数 $\lambda =\lambda \left(t\right):\left[0,T\right)\to \left[0,1\right]$ 使得对几乎所有的 $t\in \left[0,T\right)$ 有

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\alpha \lambda xy\\ \frac{\text{d}y}{\text{d}t}=-\gamma y+\beta \lambda xy\end{array}$ (2.5)

那么称向量函数 $\left(x\left(t;x_0,y_0\right),y\left(t;x_0,y_0\right)\right)$ 是系统(2.2)过初始值 $\left(x_0,y_0\right)$ 的解。

根据平衡点与切换线的相对位置，子系统的平衡点关于系统(2.2)分为实平衡点, 虚平衡点和边界平衡点三类。对于系统(2.2)， $E_1^1$ 和 $E_2^1$ 分别是虚平衡点和实平衡点； $E_1^1$ 当 $0<x_1<\theta$ 时是虚平衡点，当 $x_1>\theta$ 时为实平衡点，而当 $x_1=\theta$ 时为边界平衡点。为考虑模型(2.2)的生物学意义，需分析系统(2.2)解的有界性和正性，其结果由下面这个命题给出，证明可参考文献 [9]。

命题2.3 $\left(x\left(t\right),y\left(t\right)\right)$ 是系统(2.2)过初始值 $\left(x_0,y_0\right)$ 的解且满足 $x_0>0$ 和 $y_0>0$，则 $\left(x\left(t\right),y\left(t\right)\right)$ 的存在区间为 $\left[0,+\infty \right)$，在 $\left[0,+\infty \right)$ 上有界且 $x\left(t\right)>0$ 和 $y\left(t\right)>0$ 成立。

切换线附近的动力学行为对不连续动力系统的全局动力学分析具有重要作用，下面分析系统(2.2)在切换线 $\sum$ 附近的动力学行为，系统(2.2)在切换线 $\sum$ 可分为穿越域 ${\sum }_c$ 和滑模域 ${\sum }_s$ 两个部分，其中

${\sum }_c=\left\{\left(x,y\right)\in R_{+}^2:0<y<y_{c1},x=\theta ,y_{c1}=\frac{1-\theta }{a\alpha }\right\}$

和

${\sum }_s=\left\{\left(x,y\right)\in R_{+}^2:y_{c1}<y,x=\theta ,y_{c1}=\frac{1-\theta }{a\alpha }\right\}.$

通过对向量场的分析，系统(2.2)的解在穿越域 ${\sum }_c$ 中从左往右穿越切换线，而在滑模域 $\sum$ 中只能沿着 ${\sum }_s$ 滑动，且 ${\sum }_s$ 为吸引域。因此在滑模域 ${\sum }_s$ 上系统(2.2)具有滑模动力学，利用Filippov凸方法可计算滑模方程为

$\frac{\text{d}y}{\text{d}t}=f\left(y\right),x=\theta$ (2.6)

其中

$f\left(y\right)=-\gamma y+\frac{\beta \theta \left(1-\theta \right)}{\alpha }$ (2.7)

若存在 $y^{\ast }>y_{c1}$ 使得 $f\left(y^{\ast }\right)=0$，则称 $\left(\theta ,y^{\ast }\right)$ 为系统(2.2)的伪平衡点。注意到 $f\left(y^{\ast }\right)=0$ 存在唯一的非零正根

$y_p=\frac{\beta \theta \left(1-\theta \right)}{\alpha \gamma },$

因此系统(2.2)可能的伪平衡点为 $\left(\theta ,y_p\right)$。

命题2.4 设 $T_1=\left(x_1,\theta \right)$ 和 $y_p$ 由(2.7)所定义，则系统(2.2)

i) 当 $x_1<\theta$ 即 $\frac{\gamma }{a\beta }<\theta$ 时，存在唯一的伪平衡点 $E_p=\left(\theta ,y_p\right)$，且从 ${\sum }_s$ 出发的解沿 ${\sum }_s$ 收敛到 $E_p$ ；

ii) 当 $x_1>\theta$ 即 $\frac{\gamma }{a\beta }>\theta$ 时，不存在伪平衡点，且从 ${\sum }_s$ 出发的解沿 ${\sum }_s$ 在有限时间内到达 $T_1$。

证明：经计算可得

$f\left(y_{c1}\right)=\frac{\alpha \beta \left(1-\theta \right)}{a\alpha }\left(\theta -x_1\right)$ (2.8)

与

$\underset{y\to +\infty }{\lim }f\left(y\right)<0$ (2.9)

则当 $x_1<\theta$ 时有 $f\left(y_{c1}\right)f\left(+\infty \right)<0$。注意到 $y_p$ 是 $f\left(y\right)=0$ 的唯一正根，从而 $x_1<\theta$，即系统(2.2)存在唯一的伪平衡点 $E_p=\left(\theta ,y_p\right)$。另外由(2.7)可推出， $f^{\prime }\left(y\right)=-\gamma <0$ 因此结论(i)成立。当 $x_1>\theta$ 时有 $f\left(y\right)<0$，故结论(ii)成立。

3. 主要结果及其证明

本节将分三种情形讨论(2.2)平衡点的存在性。

情形1： $0<\frac{\gamma }{a\beta }<\theta$

在这种情况下 $E_1$ 是虚平衡点，在滑模 ${\sum }_s$ 上存在伪平衡点 $E_P$。

定理3.1 若 $0<\frac{\gamma }{a\beta }<\theta$，则系统(2.2)的伪平衡点 $E_P$ 是全局渐近稳定的。

证明：由于平衡点 $E_1$ 在系统(2.4)中是全局渐近稳定的，并且不存在包含 ${\bar{\sum }}_s$ 的滑模环，所以从区域 $G_2$ 出发的轨线将在有限时间内到达滑模与 ${\sum }_s$ 相交，从区域 $G_1$ 出发的轨线要么直接到达滑模 ${\sum }_s$ 上，要么由于点(1, 0)的稳定性，将会进入 $G_2$ 区域，并在有限时间内到达滑模，又因为伪平衡点 $E_P$ 在滑模上是稳定的，所以伪平衡点 $E_P$ 是全局渐近稳定的。

情形2： $\theta <\frac{\gamma }{a\beta }<1$

在这种情况下， $E_1$ 是实平衡点，在滑模 ${\sum }_s$ 上不存在伪平衡点 $E_P$。

定理3.2 若 $\theta <\frac{\gamma }{a\beta }<1$，则系统(2.2)的实平衡点 $E_1$ 是全局渐近稳定的。

证明：由于 $E_1$ 在系统(2.4)中的稳定性，从切点 $T_1$ 出发的任何解都不会再次到达滑模 ${\sum }_s$ 上，必将趋向于平衡点 $E_1$，从区域 $G_2$ 出发的任何轨线到达滑模 ${\sum }_s$ 之后将沿着滑模域移动到达切点 $T_1$，然后趋向于平衡点 $E_1$，所以从区域 $G_2$ 出发的任何轨线都将会收敛到 $E_1$。

从区域 $G_1$ 开始的任何解都将在有限时间内到达阈值 $x=\theta$，到达滑模 ${\sum }_s$ 的轨线都将沿着滑模域到达切点 $T_1$，然后趋向于平衡点 $E_1$，此外任何到达切点 $T_1$ 以下的轨线将进入区域 $G_2$，因此也会趋向于平衡点 $E_1$，故系统(2.2)的所有解都最终趋向于平衡点 $E_1$。

情形3： $\frac{\gamma }{a\beta }<0$

在这种情况下， $E_1$ 是虚平衡点，在滑模 ${\sum }_s$ 上不存在伪平衡点 $E_P$。

定理3.3 若 $\frac{\gamma }{a\beta }<0$，则系统(2.2)的实平衡点 $E_2^1$ 是全局渐近稳定的。

证明：由于 $E_2^1$ 在系统(2.4)中的稳定性，从切点 $T_1$ 出发的任何解都不会再次到达滑模 ${\sum }_s$ 上，必将趋向于平衡点 $E_2^1$，从区域 $G_2$ 出发的任何轨线到达滑模 ${\sum }_s$ 之后将沿着滑模域移动到达切点 $T_1$，然后趋向于平衡点 $E_2^1$，所以从区域 $G_2$ 出发的任何轨线都将会收敛到 $E_2^1$。

从区域 $G_1$ 开始的任何解都将在有限时间内到达阈值 $x=\theta$，到达滑模 ${\sum }_s$ 的轨线都将沿着滑模域到达切点 $T_1$，然后趋向于平衡点 $E_2^1$，此外任何到达切点 $T_1$ 以下的轨线将进入区域 $G_2$，因此也会趋向于平衡点 $E_2^1$，故系统(2.2)的所有解都最终趋向于平衡点 $E_2^1$。

4. 生物学意义

在自然界中捕食者与食饵的相互作用中，如果没有避难所对食饵的保护，食饵是很有可能灭绝的，因此在本文中加入了避难所的因素。先利用Lyapunov函数来对子系统平衡点的稳定性来进行判断，然后再去分析整个系统的全局动力学行为。通过分析我们可以得到：当内部平衡点不存在时，即 $\frac{\gamma }{a\beta }<0$ 时，此时捕食者和食饵是在平衡点 $E_2^1$ 处稳定的。当阈值比较大的情况下，即 $0<\frac{\gamma }{a\beta }<\theta$，此时的猎物和捕食者是可以在伪平衡状态下共同存活的(如图1)。当阈值比较小时，即 $0<\theta <\frac{\gamma }{a\beta }$，猎物和捕食者可以在实平衡的状态下一起存活下去(如图2)。本文的策略是在食饵的数量比较少的时候加入避难所对食饵进行保护。以上分析表明在合适的情况下加入猎物避难所这个措施是可行的，猎物较少的时候会进入避难所里，这

Figure 1. Curve: Global asymptotic stability of the pseudo equilibrium E_P of system (2.2)

图1. 系统(2.2)伪平衡点E_P的全局渐近稳定性

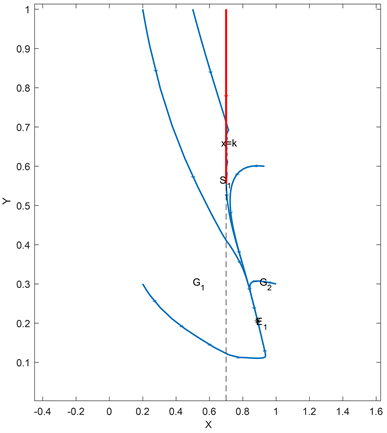
Figure 2. Curve: Global asymptotic stability of the real equilibrium E₁ of system (2.2)

图2. 系统(2.2)实平衡点E₁的全局渐近稳定性

样捕食者所能捕获猎物的机会就会变少，从而捕食者的数量会下降，避免食饵灭绝，从而保护生物的多样性。