基于原位燃烧模型的外梯度法

Extragradient Method Based on in Situ Com-bustion Model

摘要: 为了更好求解原位燃烧模型，给出了一种外梯度法。首先在离散格式上采用Crank-Nicolson中心差分方案，其次迭代算法选取外梯度法，将非线性互补问题通过投影转化为不动点方程的等价形式，进而使用外梯度法求解，最后给出该算法在满足线性收敛条件下的数值模拟结果，并与内点法进行比较，验证了该算法在解决原位燃烧模型的可行性。

Abstract: To better solve the in situ combustion model, an extragradient method is given. Firstly, the Crank-Nicolson central difference scheme is used in the discrete format, and secondly, the extra-gradient method is chosen for the iterative algorithm, which transforms the nonlinear complemen-tary problem into the equivalent form of the immobile point equation by projection, and then solves it using the extragradient method, and finally, the numerical simulation results of the algorithm are given under the condition of satisfying linear convergence, and compared with the inner point method to verify the algorithm in solving the in situ combustion. The feasibility of the algorithm in solving the in situ combustion model is verified.

1. 引言

随着科技的快速发展，工业上对石油的需求量大大增加，然而，石油作为不可再生资源，在世界范围内是非常紧张的。因此，原油的生产技术对经济发展和时代进步起着重要作用。重油作为原油在提取汽油、柴油后的剩余重质油，在提取的过程中的困难在于其高粘度。降低粘度的一般方法有蒸汽注入或原位燃烧。

原位燃烧方法(In Situ Combustion, ISC)是一种原位燃烧开采方法 [1]，在重油开采过程中发挥着重要作用，并被广泛应用 [2]。原位燃烧技术的作用原理是指将热空气注入到井中，点燃部分油层中的燃料，由于油层不断地接收氧化剂，使得油层在地下形成一个燃烧带，因此剩余原油可被继续开采 [3]。原位燃烧方法可分为向前燃烧和向后燃烧，其区分原理是根据空气的流动方向。通常将空气和燃烧峰方向相同时，称为向前燃烧。反之，将空气和燃烧峰方向相反时，称为向后燃烧。由于向后燃烧的模型不稳定，所以在过往的研究中，学者们更多采用的是向前燃烧。原位燃烧的操作环境大致分为两种，分别是干式和湿式，区别在于干式仅注入空气，湿式是将水伴随空气一起注入井中。

近年来，针对原位燃烧驱油机理，学者们进行了深入研究，使得该技术得到空前的发展。原位燃烧方法对石油的开采效果显著，使得其实际研究价值巨大，所以国内外研究学者针对该实验过程进行了大量的数值模拟工作。下面给出部分国内外研究学者的成果介绍。

1964年，Poettmann等人 [4] 给出了空气消耗量针对干式向前燃烧过程的计算理论方法。他们的研究工作成果为后续针对研究原位燃烧的数值模拟计算及室内实验做出了巨大的贡献。1960年，Willson等人 [5] 通过两种模式下室内实验数据建立起计算公式，两种模式分别为干式向前燃烧室内实验及湿式向前燃烧室内实验。1962年，众多研究学者针对影响原位燃烧的因素进行了深入研究，例如，Alexander针对燃料燃烧与初始含油率的相关程度大小的研究 [6]。1991年，Adewusi等人研究发现氧气在注入口处的浓度值，对原位燃烧具有一定程度的影响，但是并非是氧气浓度越高，采油率越高，而是在氧气浓度处于35%时，采油效果最好 [7]。

由于科学技术和优化算法的发展，越来越多的学者通过数值模拟的方法对原位燃烧过程进行研究。1979年~1980年，Crookston [8] 和Coats [9] 针对原位燃烧提出了数学模型。Coats将原位燃烧过程简化成多孔介质内伴随着化学反应的多相多组分流动问题，并给出了相应的控制方程，并且对于注入氧气时是否伴有水的注入没有限制。此模型的提出，解决了可以同时求解多个化学反应的问题。由于其优越性，后续学者往往会选择该数学模型进行研究。2011年，Mailybaev等人将原位燃烧中复杂的化学反应简化成一个简单的氧化反应： $\text{C}+{\text{O}}_2\to {\text{CO}}_2$。并验证了化学式可以正确模拟原位燃烧的反应过程，为后续研究的学者简化了原位燃烧数学模型 [10]。2016年，Chapiro等人将原位燃烧数学模型改写成一个混合非线性互补问题的形式，并利用内点法分别结合有限元方法及有限差分法进行数值模拟。相较于传统方法，引入优化算法，为后续的研究提供了新的思路 [11]。

通过对于上述研究的梳理，目前对于原位燃烧的研究主要以实验室实验和建立数学模型为主。然而，针对数值模拟方法的研究成果尚且不多，因此选择更优的数值模拟方法，对进一步推动该技术的发展显得尤为重要。

2. 原位燃烧模型

针在原位燃烧过程中，由于燃料只占据了小部分可用空间，因此反应中孔隙率的变化是可以忽略的，对于其它燃烧反应过程中的变量，由于固体和气体的温度相同，因此热损失可以忽略，并且考虑氧气是充足的。因此，原位燃烧过程可以建立为一个简化的数学模型。本章给出由两个非线性微分方程组成的简化原位燃烧模型。该模型是由Akkutlu和Yortsos提出 [12]。

下面给出原位燃烧数学模型的具体形式，该模型包括热平衡方程(2.1)和燃料的摩尔平衡方程以及理想气体定律(2.2)，即

$C_m\frac{\partial T}{\partial t}+\frac{\partial \left(c_g\rho \omega \left(T-T_{res}\right)\right)}{\partial x}=\lambda \frac{{\partial }^{2}T}{\partial x^2}+Q_r{W}_r,$ (2.1)

$\frac{\partial {\rho }_f}{\partial t}=-{\mu }_f{W}_r,T=P/\left(\rho R\right).$ (2.2)

其中 $T\left[\text{K}\right]$ 为温度， $\rho \left[\text{mole}/{\text{m}}^{\text{3}}\right]$ 为气体的摩尔密度， ${\rho }_f\left[\text{mole}/{\text{m}}^{\text{3}}\right]$ 为固体燃料的体积摩尔浓度。t和x分别代表时间坐标及空间坐标， $T,\rho$ 和 ${\rho }_f$ 为未知数，剩余变量均为常数，其具体数值在表1中给出。

Table 1. In situ combustion parameter values

表1. 原位燃烧参数值

原位燃烧是非常复杂的过程，包含若干化学反应。但是，为了简化其过程，本章只考虑 $\text{C}+{\text{O}}_2\to {\text{CO}}_2$ 的化学反应。因此，易得出式(2.2)中 ${\mu }_f$ 的值为1。无限量供氧的反应速率 $W_r$ 表示为，

$W_r=k_p{\rho }_f\exp \left(-E_r/\left(RT\right)\right),$ (2.3)

其中， $k_p$ 和 $E_r$ 的数值可从表1中得到。

本文给出式(2.1)~(2.2)的无量纲形式，其中自变量和因变量的无量纲形式用波浪号表示。量纲量和参考量的比值，用星号表示，

$\tilde{t}=\frac{t}{t^{*}},\tilde{x}=\frac{x}{x^{*}},\tilde{\theta }=\Delta \tilde{T}=\frac{T-T_{res}}{\Delta T^{*}},\tilde{\rho }=\frac{\rho }{{\rho }^{*}},\tilde{\eta }=1-\frac{{\rho }_f}{{\rho }_f^{*}},\tilde{\omega }=\frac{{\omega }_{inj}}{{\omega }^{*}}.$ (2.4)

参考量的数值如下，

$\begin{array}{l}{t}^{*}=Q_r{\rho }_f^{res},{\rho }^{*}=P/\left(R{T}_{res}\right),\Delta T^{*}=t^{*}/C_m,x^{*}=c_g\\ {\rho }^{*}\Delta T^{*},{\rho }_f^{*}={\rho }_f^{res},{\omega }^{*}=x^{*}/t^{*},\end{array}$ (2.5)

其中， $T_{res}$ 和 ${\rho }_f^{res}$ 分别表示初始储层温度和燃料摩尔密度， ${\omega }_{inj}$ 是注入气体速度。式 中， $t^{*}$ 是燃料在初始储层温度 $T_{res}$ 下燃料燃烧的特征时间， $\Delta T^{\text{*}}$ 是燃料在绝热条件下完全燃烧时峰值温度与储层温度的差值。

根据式(2.4)~(2.5)，将原位燃烧方程转化为以下无量纲形式，即

$\frac{\partial \theta }{\partial t}+\omega \frac{\partial \left(\rho \theta \right)}{\partial x}=\frac{1}{P{e}_T}\frac{{\partial }^2\theta }{\partial x^2}+\Gamma ,$ (2.6)

$\frac{\partial \eta }{\partial t}=\Gamma ,$ (2.7)

$\rho ={\theta }_0/\left(\theta +{\theta }_0\right),$ (2.8)

$\Gamma =\beta \left(1-\eta \right)\exp \left(-\frac{\mathcal{E}}{\theta +{\theta }_0}\right).$ (2.9)

其中， $\theta$ 表示标度温度， $\eta$ 表示石油工程中常用的固定燃料深度，当 $\eta =0$ 时，燃料达到最大值，当 $\eta =1$ 时，表示没有燃料。 $P{e}_T$ 表示热扩散过程的佩克莱数， $\omega$ 是无量纲气体速度， $\epsilon$ 是标度活化能， ${\theta }_0$ 是标度储层温度。上述变量均为常数，下面给出其在无量纲参数值 $P{e}_T=1406$， $\beta =7.44\times {10}^{10}$， $\mathcal{E}=93.8$， ${\theta }_0=3.67$， $u=3.76$。系统在初始储层条件下进行求解，

$t=0,x\ge 0:\theta =0,\eta =0,$ (2.10)

与其对应的左边界条件：

$t\ge 0,x=0:\theta =0,\eta =1.$ (2.11)

3. 算法设计

非线性互补问题的一般形式，为求解 $u\in R^n$，满足

$u\ge 0,F\left(u\right)\ge 0,u^{\text{T}}F\left(u\right)=0,$ (3.1)

根据非线性互补理论，可以将抛物型偏微分方程转化为非线性互补形式，并将该形式求解移动边界问题。过往研究中，Chapiro [11] 提出了应用非线性互补问题的可行方向法(FDA-NCP)，去求解原位燃烧方程。基于该研究成果，本文进一步利用非线性互补理论中的外梯度法求解原位燃烧方程。

本文主要研究内容是利用外梯度法求解原位燃烧方程，然而该方程无法直接应用外梯度法进行求解，需要先将其转换为非线性互补形式，进而使用有限差分法和外梯度法相结合的求解算法。这里，首先给出可应用非线性互补算法的变分形式，即

$\theta \ge 0,\eta \ge 0;\frac{\partial \theta }{\partial t}+\omega \frac{\partial \left(\rho \theta \right)}{\partial x}-\frac{1}{P{e}_T}\frac{{\partial }^2\theta }{\partial x^2}-\Gamma \ge 0;\frac{\partial \eta }{\partial t}-\Gamma \ge 0;$ (3.2)

$\left(\frac{\partial \theta }{\partial t}+\omega \frac{\partial \left(\rho \theta \right)}{\partial x}-\frac{1}{P{e}_T}\frac{{\partial }^2\theta }{\partial x^2}-\Gamma \right)\theta =0;\left(\frac{\partial \eta }{\partial t}-\Gamma \right)\eta =0.$ (3.3)

其次，由于投影算法是非线性互补算法的一种，针对投影类型算法的等价非线性互补形式可以表示为：

$\begin{array}{l}\theta \ge 0,\eta \ge 0;\alpha \left(\frac{\partial \theta }{\partial t}+\omega \frac{\partial \left(\rho \theta \right)}{\partial x}-\frac{1}{P{e}_T}\frac{{\partial }^2\theta }{\partial x^2}-\Gamma \right)\ge 0;\alpha \left(\frac{\partial \eta }{\partial t}-\Gamma \right)\ge 0;\\ \alpha \left(\frac{\partial \theta }{\partial t}+\omega \frac{\partial \left(\rho \theta \right)}{\partial x}-\frac{1}{P{e}_T}\frac{{\partial }^2\theta }{\partial x^2}-\Gamma \right)\theta =0,\alpha \left(\frac{\partial \eta }{\partial t}-\Gamma \right)\eta =0.\end{array}$ (3.4)

由于 $\alpha >0$，且式(3.2)成立，易计算得式(3.4)满足非线性互补条件。

上述研究内容，将原位燃烧方程改写成了可应用非线性互补算法的变分形式，由于原位燃烧问题是一个典型的非线性问题，获得其解析解十分困难，因此需要对该方程进行线性化处理，这就需要用到有限差分法进行离散。

本文针对原位燃烧模型使用Crank-Nicolson有限差分格式，该离散格式的优势在于，其为无条件稳定的，并且可以选取更大的时间步长，使得降低每个时间步内迭代算法的误差。下述给出针对原位燃烧变分形式的离散过程。

设 $F_{\Delta }^1\left(\theta ,\eta \right)$ 和 $F_{\Delta }^2\left(\theta ,\eta \right)$ 是对应于不等式(3.4)左侧的微分算子，

$F_{\Delta }\left(\theta ,\eta \right)={\left[F_{\Delta }^1\left(\theta ,\eta \right),F_{\Delta }^2\left(\theta ,\eta \right)\right]}^{\text{T}}.$ (3.5)

其中

$\begin{array}{l}{F}_{\Delta }^1\left(\theta ,\eta \right)={\theta }_m^{n+1}-{\theta }_m^n+\omega \Delta t\frac{{\rho }_{m+1}^{n+1}{\theta }_{m+1}^{n+1}-{\rho }_{m-1}^{n+1}{\theta }_{m-1}^{n+1}}{4\Delta x}+\omega \Delta t\frac{{\rho }_{m+1}^n{\theta }_{m+1}^n-{\rho }_{m-1}^n{\theta }_{m-1}^n}{4\Delta x}\\ -\frac{\Delta t}{P{e}_T}\frac{{\theta }_{m-1}^{n+1}-{\theta }_m^{n+1}+{\theta }_{m+1}^{n+1}}{2\Delta x^2}-\frac{\Delta t}{P{e}_T}\frac{{\theta }_{m-1}^n-2{\theta }_m^n+{\theta }_{m+1}^n}{2\Delta x^2}-\frac{\Delta t\left({\Gamma }_m^{n+1}+{\Gamma }_m^n\right)}{2},\\ F_{\Delta }^2\left(\theta ,\eta \right)={\eta }_m^{n+1}-{\eta }_m^n+\frac{\Delta t\left({\Gamma }_m^{n+1}+{\Gamma }_m^n\right)}{2}.\end{array}$ (3.6)

基于以上分析，有限差分法的实质就是将原方程中的微分算子替换为离散算子，即将式(3.3)中的 $F^1\left(\theta ,\eta \right)$ 和 $F^2\left(\theta ,\eta \right)$ 替换为 $F_{\Delta }^1\left(\theta ,\eta \right)$ 和 $F_{\Delta }^2\left(\theta ,\eta \right)$。具体操作是将左边关于时间变量的 $n+1$ 项离散，得到时间变量的非线性方程组。其中，关于点 $m=0$ 和 $m=M$ 处的方程用边界条件替代。

原位燃烧问题是典型的移动边界问题，因此该问题的边界具有未知性。如何确定移动边界的位置是本章的重点研究内容。针对左侧的边界条件，由于温度恒定且无燃料，根据上述关于原位燃烧方程的介绍，可得 $\theta \left(x_0,t\right)=0$ 和 $\eta \left(x_0,t\right)=1$， $t\ge 0$。然而对应于右侧的边界，由于该边界无固定位置，因此将其模拟为零流Neumann边界条件。

下述针对每个时间步应用的外梯度法 [13] 进行研究。

算法 1

步骤0 (初始步)给定初始点 $u^0\in R^n$， $0\Rightarrow k$。

步骤1 (预测步)若 $u^k$ 不是式(3.3)的解，则令

${\bar{u}}^k={\left[u^k-{\alpha }_{k}F\left(u^k\right)\right]}_{+},$ (3.7)

这里 ${\alpha }_k=\gamma l^{m_k}\left(\gamma >0,l\in \left(0,1\right)\right)$， $m_k$ 是使下式成立的最小非负整数：

$\Vert F\left(u^k\right)-F\left({\bar{u}}^k\right)\Vert \le \mu \cdot \frac{\Vert u^k-{\bar{u}}^k\Vert }{{\alpha }_k},\mu \in \left(0,1\right)$ (3.8)

步骤2 (校正步)让

$u^{k+1}={\left[u^k-{\alpha }_{k}F\left({\bar{u}}^k\right)\right]}_{+}.$ (3.9)

步骤3 $k+1\Rightarrow k$，返回步骤1。

算法1中，步骤1的线搜索并不是经典的线搜索。由于式(3.8)每进行一次投影，才可以更新 ${\alpha }_k$。因此，式(3.8)是弯曲搜索。通过结合算法1和Crank-Nicolson中心差分格式，给出求解原位燃烧问题的主算法。

算法 2

步骤0 给定初始变量 $u_M^0,m=0,1,\cdots ,M$ 和初始时间步长 $\Delta t_0$ ；

步骤1 利用有限差分法获得基于互补形式的非线性方程组；

步骤2 使用算法1求解步骤1中的非线性方程组；

步骤3 在下一个时间步骤中，将步骤3中的解值赋下一个时间差分步长中初始变量u；

步骤4 返回步骤2中的算法，直到时间差分网格全部计算完毕。

4. 数值实验

本节进行数值实验，为了验证外梯度法对于求解原位燃烧问题的有效性，离散方法上都选取Crank-Nicolson有限差分格式，在每个时间步的求解算法上分别选取FDA-NCP算法及牛顿法相对比。

本文的离散处理方式为在空间变量上选择固定网格，时间变量上选择恒定时间网格步长 $k={10}^{-5}$。为了增加算法的适用性，本文选择两种不同的空间网格步长h进行数值模拟。

图1~3给出选取固定空间网格步长为 $k={10}^{-5}$ 时，算法2与有限差分法和FDA-NCP算法相结合的求解算法分别在 $t=0.001,t=0.004,t=0.008$ 时温度及燃料深度的分布曲线图。另外，从图中可以看出，很明显可以看出选取相同时间，两种算法的曲线几乎完全相同，实验结果验证了算法2对于求解原位燃烧问题的可行性。

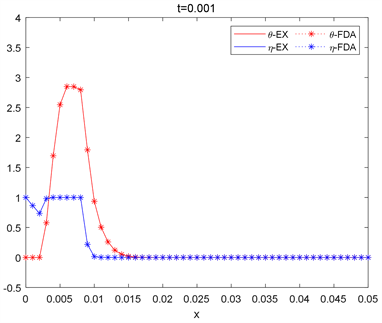
Figure 1. The two algorithms correspond to the solution of the h = 0.02 spatial grid step at time $t=0.001$

图1. 两种算法对应于 $h=0.02$ 空间网格步长在时间 $t=0.001$ 时的解

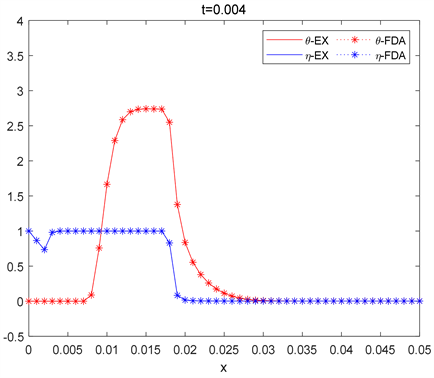
Figure 2. The two algorithms correspond to the solution of the h = 0.02 spatial grid step at time $t=0.004$

图2. 两种算法对应于 $h=0.02$ 空间网格步长在时间 $t=0.004$ 时的解

Figure 3. The two algorithms correspond to the solution of the h = 0.02 spatial grid step at time $t=0.008$

图3. 两种算法对应于 $h=0.02$ 空间网格步长在时间 $t=0.008$ 时的解

图4~6给出选取固定空间网格步长为 $h=0.02$ 时，算法2与有限差分法和FDA-NCP算法相结合的求解算法分别在 $t=0.001,t=0.004,t=0.008$ 时温度及燃料深度的分布曲线图。相比较于图1~3，减小了固定空间网格步长，使模拟精度更高，从图中依然可以明显看出，两种算法的曲线几乎相同，因此对比精度更高时，算法2对于求解原位燃烧方程依然有效。

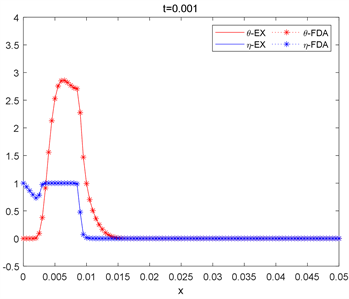
Figure 4. The two algorithms correspond to the solution of the h = 0.005 spatial grid step at time t = 0.001

图4. 两种算法对应于h = 0.005空间网格步长在时间t = 0.001时的解

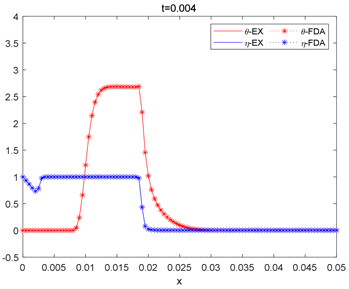
Figure 5. The two algorithms correspond to the solution of the h = 0.005 spatial grid step at time t = 0.004

图5. 两种算法对应于h = 0.005空间网格步长在时间t = 0.004时的解

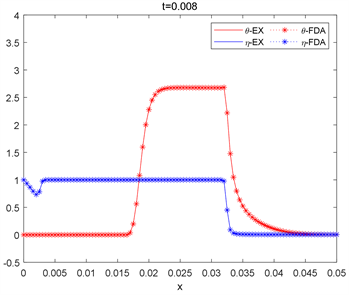
Figure 6. The two algorithms correspond to the solution of the h = 0.005 spatial grid step at time t = 0.008

图6. 两种算法对应于h = 0.005空间网格步长在时间t = 0.008时的解

图7~9给出选取固定空间网格步长为 $h=0.005$ 时，算法2与有限差分法和牛顿法相结合的求解算法分别在 $t=0.002,t=0.006,t=0.010$ 时温度及燃料深度的分布曲线图。从图中可以看出，很明显可以看出选取相同时间，两种算法的曲线几乎完全相同。另外，可以看出当本文选择较大的空降网格步长时，牛顿法会出现发散的现象，因此算法2对于求解原位燃烧方程具有更好的收敛性。

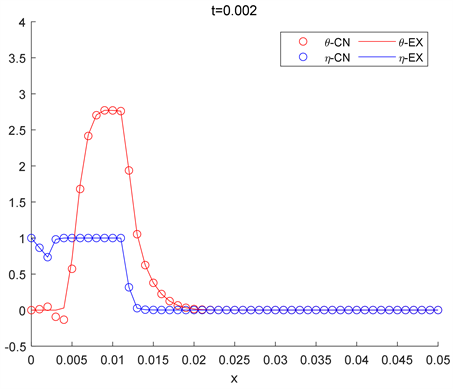
Figure 7. The two algorithms correspond to the solution of the h = 0.02 spatial grid step at time t = 0.002

图7. 两种算法对应于h = 0.02空间网格步长在时间t = 0.002时的解

Figure 8. The two algorithms correspond to the solution of the h = 0.02 spatial grid step at time t = 0.006

图8. 两种算法对应于h = 0.02空间网格步长在时间t = 0.006时的解

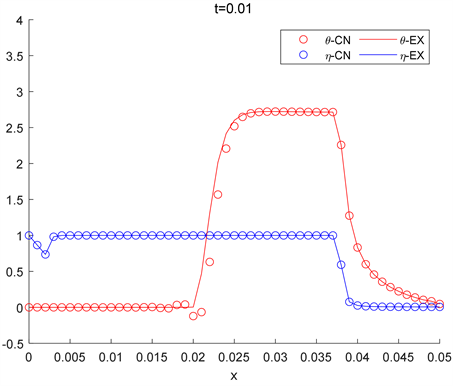
Figure 9. The two algorithms correspond to the solution of the $h=0.02$ spatial grid step at time $t=0.01$

图9. 两种算法对应于 $h=0.02$ 空间网格步长在时间 $t=0.01$ 时的解

图10~12给出选取固定空间网格步长为 $h=0.02$ 时，算法2与有限差分法和牛顿法相结合的求解算法分别在 $t=0.002,t=0.006,t=0.010$ 时温度及燃料深度的分布曲线图。并且可以看出，在选取空间网格步长更小时，牛顿法的发散现象会消失。

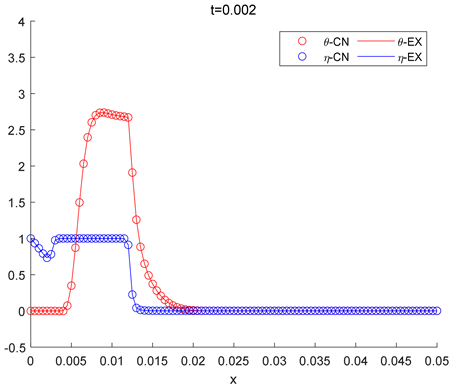
Figure 10. The two algorithms correspond to the solution of the $h=0.005$ spatial grid step at time $t=0.002$

图10. 两种算法对应于 $h=0.005$ 空间网格步长在时间 $t=0.002$ 时的解

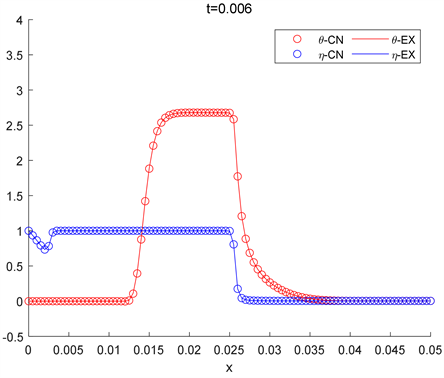
Figure 11. The two algorithms correspond to the solution of the $h=0.005$ spatial grid step at time $t=0.006$

图11. 两种算法对应于 $h=0.005$ 空间网格步长在时间 $t=0.006$ 时的解

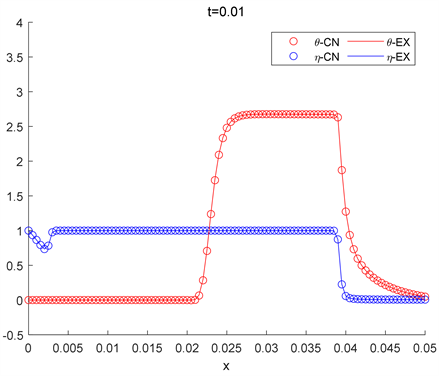
Figure 12. The two algorithms correspond to the solution of the $h=0.005$ spatial grid step at time $t=0.01$

图12. 两种算法对应于 $h=0.005$ 空间网格步长在时间 $t=0.01$ 时的解

5. 结论

本文设计了结合有限差分格式和外梯度法的高效算法来求解原位燃烧模型。首先，使用Crank-Nicolson中心有限差分法对偏微分方程进行离散，得到非线性程组，同时利用外梯度法进行该方程组。其中第一步使用投影公式确定迭代点作为预测点，然后将预测点再次使用投影公式确定校正点，并将其作为新的迭代点，并给出该算法的收敛性分析。最后，进行数值实验模拟，将算法2分别与牛顿法和FDA-NCP算法进行对比，结果表明外梯度法对于求解原位燃烧模型的可行性。外梯度法作为投影类算法的一种，相比较于牛顿法和FDA-NCP算法无需求解梯度信息，直接选取向量 $-F\left({\bar{u}}^k\right)$ 为下降方向，并且计算更为简单且存储量较小。