秦皇岛某深基坑锚桩支护结构设计方法对比分析

Comparative Analysis of Design Methods of Anchor Pile Support Structure in a Deep Foundation Pit in Qinhuangdao

摘要: 分别采用静力平衡法和等值梁法对秦皇岛某深基坑工程的单支点桩锚支护结构进行设计，对比分析了嵌固深度、锚杆轴向拉力和桩身最大弯矩设计值的计算值。结果表明在这类场地地层条件下，采用静力平衡法计算桩身最大弯矩利于工程安全，采用等值梁法确定嵌固深度和锚杆轴向拉力利于工程安全，这两种设计方法可为类似深基坑支护工程设计提供参考。

Abstract: The static balance method and equivalent beam method are used to design the single fulcrum pile anchor support structure of a deep foundation pit project in Qinhuangdao. The calculation results of embedded depth, axial tension of anchor rod and design value of maximum bending moment of pile body are compared and analyzed. Under such site stratigraphic conditions, it shows that calculating the maximum bending moment of pile body by static balance method is beneficial to engineering safety. The equivalent beam method is used to determine the embedded depth and axial tension of anchor rod, which is conducive to engineering safety. These two design methods can provide reference for the design of similar deep foundation pit support engineering.

1. 引言

改革开放40多年以来，随着我国经济建设的高速发展，各地尤其是沿海经济较发达城市兴建了大量的各类建筑。大规模的高层建筑地下室、地下商场的建设和大规模的市政工程如地下停车场、大型地铁车站、地下变电站、大型排水及污水处理系统等的施工都涉及深基坑工程。由于功能要求日益复杂、支护体系种类繁多、各种施工工艺的联合使用，发展出了一系列支护技术如水泥土重力式围护墙、土钉墙、灌注桩排桩、SMW工法、地下连续墙、土层锚杆和钢支撑等，为各类基坑工程的支护提供了有效的技术手段 [1] [2] [3] [4]。本文介绍秦皇岛一深基坑工程所采用的支护设计方法。

2. 工程概况

秦皇岛一拟建高层公寓地上34层，地下2层。拟建高层公寓基础埋深−9.2 m，基坑开挖深度约8.6 m，开挖面积约1400 m²。拟建高层公寓南侧距一栋6层住宅楼18 m，6层住宅楼为预制桩基础，桩长9 m；东侧距一栋19层住宅楼17 m，其中地下室楼梯距离该19层住宅楼6 m，该19层住宅楼基础埋深6 m。

3. 工程地质与水文地质条件

3.1. 工程地质条件

拟建场地土层自上而下依次为填土①层、粉质粘土②层、砂土③层、粉质粘土④层、中砂⑤层和粗砂⑥层，各土层分布及物理力学性质见表1。

Table 1. Site soil layer distribution and physical and mechanical property parameters

表1. 场地土层分布及物理力学性质参数

3.2. 水文地质条件

该场地地下水主要为第四系孔隙水，主要赋存于砂层中，虽然第④层粉质粘土属弱透水层，但该层主要分布于场地西北部，在整个场地分布不连续，未起到隔水作用。

勘察期间初见地下水位埋深−2.7~−3.7 m，稳定地下水位埋深−1.2~−2.2 m。地下水补给来源为大气降水和地下水径流。地下水年变化幅度约1.0 m。含水层综合渗透系数19.7 m/d，影响半径约226 m。

4. 桩锚支护结构设计

基坑工程中，常采用静力平衡法和等值梁法进行桩锚支护结构设计。静力平衡法亦称自由端支承法，该法假定支护结构是刚性的，并可绕支撑点转动。支护结构的前侧产生被动土压力，后侧产生主动土压力。静力平衡法适用于支护结构的入土深度不太深即底端非嵌固的情况，此时支护结构由于土压力的作用而达到极限平衡状态，利用支护结构前后土压力的极限平衡条件来求插入深度、结构内力等 [5] [6] [7]。

等值梁法计算单支撑(锚拉)埋深板桩时，将其视为上端简支、下端固定支承，变形曲线有一反弯点，一般认为该点弯矩值为零。可把挡土结构划分为两段假想梁，上部为简支，下部为一次超静定结构，其弯矩图不变 [8] [9] [10]。

对于基坑南侧距一栋6层住宅楼18 m，采用单支点桩锚支护结构型式，下面分别采用这两种方法设计单支点桩锚支护结构，比较结果差异，探求利于基坑工程安全的设计方法。

因勘察报告提供的粘聚力c和内摩擦角φ为水下参数，降水后可适当提高，坑内土层加权平均后取γ = 20 kPa、φ = 32˚；对主动侧土压力的c、φ值加权平均后，c = 2.2 kPa、φ = 29.8˚，等效内摩擦角φ = 30.6˚ (按抗剪强度相等确定)。由于管井将地下水降至基坑以下，所以不考虑侧向水压力。计算时取地面超载76 kPa (计入冠梁以上土层重度)计算简图见图1。

Figure 1. Calculation diagram

图1. 计算简图

4.1. 静力平衡法

静力平衡法是一种基于单锚浅桩的设计计算方法。这种状态的支护结构插入基坑底面深度较小，桩身只有一个方向的弯矩(除去支点以上的部分)，桩身入土部分的位移较大，这时可把支护结构的上部视为简支，下端为自由支承，它的作用相当于单跨简支梁，其土压力分布图、弯矩分布图、桩身变形图见图2。

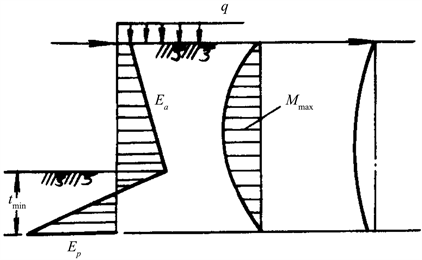
Figure 2. Soil pressure distribution, bending moment and pile deformation

图2. 土压力分布、弯矩和桩身变形图

主要计算过程：先对支点取矩，求出桩的入土深度，然后根据水平向合力为零求出支点力，最后求出剪力为零处的最大弯矩。计算简图及土压力分布见图3。

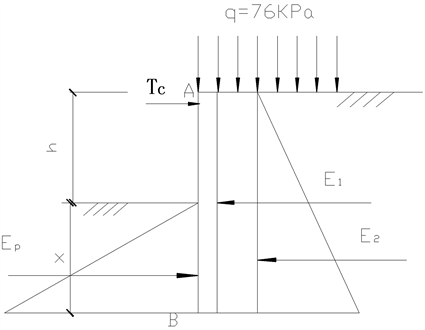
Figure 3. Soil pressure distribution and calculation diagram

图3. 土压力分布及计算简图

1) 土压力系数

$\{\begin{array}{c}{K}_a={\tan }^2\left({45}^{\circ }-\phi /2\right)\\ K_p={\tan }^2\left({45}^{\circ }+\phi /2\right)\end{array}$ (1)

式(1)中：

$K_a$ ——主动土压力系数；

$K_p$ ——被动土压力系数；

$\phi$ ——等值内摩擦角，代入数据得：

$K_a=0.33$ ； $K_p=3.25$。

2) 土压力

$\{\begin{array}{l}{E}_1=q\cdot \left(h+x\right)\cdot Ka=25.08\left(6+x\right)\underset{}{}\hfill \\ E_2=\frac{1}{2}\gamma \cdot Ka\cdot {\left(h+x\right)}^2=3.3{\left(x+6\right)}^2\hfill \\ E_p=\frac{1}{2}\gamma \cdot Kp\cdot x^2=32.5x^2\hfill \end{array}$ (2)

式(2)中：

$\gamma$ ——土的加权重度；

$E_1$ ——地面超载q产生的主动土压力；

$E_2$ ——土体自重产生的主动土压力；

$E_p$ ——被动土压力；

$h$ ——基坑开挖深度；

$x$ ——桩的入土深度。

3) 嵌固深度 $h_d$

支点A位于桩顶之下0.2 m，对支点A取矩，由 ${\displaystyle \sum M_A}=0$，代入数据解出：x = 3.2 m，将此值乘以安全系数1.2，得嵌固深度设计值 $h_d=1.2x=3.8\text{m}$。

4) 支点力(锚杆水平拉力) $T_c$

$\{\begin{array}{l}{T}_c=E_1+E_2-E_p\hfill \\ T=\frac{2\times L\times T_c}{\cos \theta }\hfill \end{array}$ (3)

式(3)中：

$T_c$ ——单位长度锚杆水平拉力标准值；

$T$ ——锚杆轴向拉力标准值；

$\theta$ ——锚杆孔的倾角，本工程中为15˚；

$L$ ——桩的间距，两桩一锚，取1.2 m，其它参数同上。

代入数据，得：

$T=\frac{2.4\times T_c}{\cos \theta }=\frac{2.4\times 177.3}{\cos {15}^{\circ }}=440.5\text{kN}$。

5) 桩身截面最大弯矩 $M_{max}$

截面最大弯矩发生在剪力为零处，剪力为零处满足：

$1/2\cdot y^2\cdot \gamma \cdot K_a+q\cdot K_a\cdot y-T_c=0$ (4)

式(4)中：

$y$ ——剪力零点至桩顶的距离，其它参数同上。

代入数据，得y = 4.4 m。

最大弯矩计算公式如下：

$\{\begin{array}{l}{M}_c=T_c\cdot \left(y-0.2\right)-\frac{q{K}_a\cdot y^2}{2}-\frac{\gamma \cdot K_a\cdot y^3}{6}\hfill \\ M_{\max }=L\times M_c\hfill \end{array}$ (5)

式(5)中：

$M_c$ ——单位长度截面最大弯矩计算值；

$M_{\max }$ ——截面最大弯矩计算值，其它参数同上。

代入数据，得：

$M_c=T_c\times 4.2-12.54\times y^2-1.1\times y^3=408.2\text{kN}\cdot \text{m}$

$M_{\max }=1.2\times M_c=489.8\text{kN}\cdot \text{m}$

所以最大弯矩设计值为489.8 kN∙m。

4.2. 等值梁法

等值梁法的基本原理如图4所示：图中ab梁一端固定，另一端简支，弯矩图的正负弯矩在c点转折。若将梁ab在c点切断，并于点c置一自由支承，形成ac梁，则ac梁上的弯矩将保持不变，即称ac梁为ab梁上ac段的等值梁。等值梁法的土压力分布及计算简图见图5。

Figure 4. Equivalent beam method

图4. 等值梁法

应用等值梁法计算，首先应知正负弯矩转折点的位置，一般取土压力为零处作为反弯点。

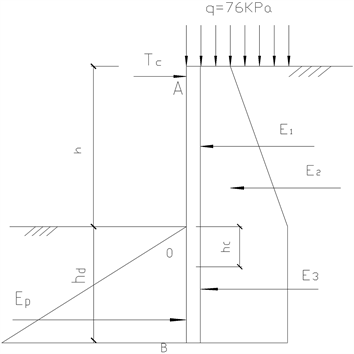
Figure 5. Soil pressure distribution and calculation diagram

图5. 土压力分布及计算简图

1) 土压力参数

同上， $K_a=0.33$、 $K_p=3.25$。

2) 土压力

同上， $E_1=q\cdot h\cdot K_a=25.08\times 6=150.5\text{kN/m}$ ； $E_2=\frac{1}{2}\gamma \cdot h^2\cdot K_a=36\times 3.3=118.8\text{kN/m}$。

3) 土压力零点(即反弯点) O的深度 $h_c$

由 $e_a=e_p$，得：

$\gamma \cdot h_c\cdot K_p=\left(q+\gamma \cdot h\right)\cdot K_a$

式中：

$h_c$ ——土压力零点至基坑底面的距离；

代入数据，得 $h_c=1.0\text{m}$。

进而算出：

$\begin{array}{l}{E}_3=\left(q+\gamma \cdot h\right)\cdot K_a\cdot h_c=196\times 0.33\times 1.0=64.7\text{kN/m}\\ E_p=\frac{1}{2}\gamma \cdot h_c{}^2\cdot K_p=32.5\text{kN/m}\end{array}$

其中， $E_3$ ——基坑至反弯点间的主动土压力；

$E_p$ ——基坑至反弯点间的被动土压力。

4) 支点力 $T_c$

对O点取矩，由 ${\displaystyle \sum M_O=0}$，代入数据，得：

$T_c\cdot 6.8=150.5\times 4+118.8\times 3+64.7\times 0.5-32.5\times 0.33$

解得： $T_c=144.1\text{kN/m}$。

由式(3)得：

$T_d=1.25{\gamma }_0{T}_c=180.1\text{kN/m}$ ；

$T=\frac{2.4\times T_d}{\cos {15}^{\circ }}=447.4\text{kN}$ ；

所以锚杆轴力设计值为447.4 kN。

5) 嵌固深度 $h_d$

按基坑规程公式有 $h_p{E}_p+T_c\left(h+h_d\right)-1.2{\gamma }_0{h}_i{\displaystyle \sum E_i}\ge 0$

展开为：

$\{\begin{array}{l}{h}_p{E}_p+T_c\left(h+h_d-0.2\right)-1.2{\gamma }_0\left(E_1\cdot h_1+E_2{h}_2+E_3{h}_3\right)\ge 0\hfill \\ E_p=\frac{1}{2}\gamma \cdot h_d^2\cdot K_p\hfill \\ E_3=\left(q+\gamma \cdot h\right)K_a\cdot h_d\hfill \end{array}$ (6)

式(6)中：

$h_p$ ——合力 $E_p$ 距桩底的距离；

${\gamma }_0$ ——建筑基坑侧壁重要性系数，本基坑为二级基坑，取1.0；

$h_i$ ——合力 $E_i$ 距桩底的距离；

$h_d$ ——嵌固深度设计值；

$E_p$ ——基坑至桩端的被动土压力；

$E_3$ ——基坑至桩端的主动土压力，其它参数同上。

代入数据，得： $h_d=6.2\text{m}$。

6) 桩身截面最大弯矩 $M_{max}$

截面最大弯矩发生在剪力为零处，由式(4)得：

$3.3y^2+25.08y-144.1=0$

解出：y = 3.8 m。

由式(5)得：

$M_c=144.1\times 3.8-12.54\times {3.8}^2-1.1\times {3.8}^3=\text{277}\text{.3}\text{kN}\cdot \text{m/m}$ ；

$M=1.25{\gamma }_0{M}_c=346.6\text{kN}\cdot \text{m/m}$ ；

$M_{\max }=1.2\times M=420.0\text{kN}\cdot \text{m}$。

4.3. 两种设计方法的对比分析

两种设计方法的计算结果对比见表2。

Table 2. Comparison of calculation results

表2. 计算结果对比表

从表2可以看出，对于嵌固深度设计值，静力平衡法计算为3.8 m、等值梁法计算为6.2 m；等值梁法计算结果偏于安全，建议采用等值梁法确定嵌固深度。

对于锚杆轴向拉力设计值，等值梁法的计算结果为447.4 kN，静力平衡法设计结果为440.5 kN；为确保工程安全，建议采用等值梁法确定锚杆的选材和性能参数。

对于桩身最大弯矩设计值，静力平衡法计算结果较高，为489.8 kN∙m，等值梁法计算结果较低，为420 kN∙m，为确保工程安全，建议采用静力平衡法的计算结果进一步确定桩身配筋。

5. 结论

本文使用静力平衡法和等值梁法对单支点桩锚支护结构进行设计，分别计算了嵌固深度设计值、锚杆轴向拉力设计值和桩身最大弯矩设计值，结果表明，在该工程场地地层条件下，采用静力平衡法计算桩身最大弯矩利于工程安全，采用等值梁法确定嵌固深度和锚杆轴向拉力利于工程安全，这两种设计方法可为类似深基坑支护工程设计提供参考。