考虑分布式电源及新能源汽车的配电网拓展规划

Consider the Distribution Network Expansion Planning of Distributed Power Supply and New Energy Vehicles

摘要: 在国家快速、大力发展新能源的政策和乡村经济振兴的背景下现代乡村的配电网开始出现越来越多的新能源分布式电源和新能源汽车充电负荷接入的现象。在此背景下，老的配电网拓展规划模型可能不再适用。本文先对新能源汽车充电负荷模型进行了分析和近似处理，之后构建了配电网规划模型与目标函数，并通过不同树分别与理想中最优树比较选择出实际最优方案。最后采用33节点系统进行了案例计算。

Abstract: Under the background of China’s rapid and vigorous new energy policy and rural economic revitalization, more and more new energy distributed power sources and new energy vehicle charging load access appear in modern rural distribution network. In this context, the old distribution network expansion planning model may not be applicable. In this paper, the charging load model of new energy vehicles is analyzed and approximately processed, and then the distribution network planning model and objective function are constructed. The actual optimal scheme is selected by comparing different trees with the optimal tree in the ideal. Finally, a 33-node system is used for case calculation.

1. 引言

在发展新能源电源和乡村振兴的政策背景下，乡村配电网中接入了大量分布式新能源电源和充电汽车，然而分布式电源发电的随机性和波动性 [1]，以及充电汽车充电的无需充电行为对现有乡村配电网的规划带来极大的挑战，因此，考虑新建分布式能源和充电汽车接入等随机性对新乡村配电网规划的影响具有重大意义。

目前，对于分布式电源大量接入配电网规划的研究，因农村的住宅一般以平房为主，有着大量的屋顶资源可以利用且风力资源丰富，在近年来国家对太能发电、风能的补贴下，农村的太阳能、风能井喷式发展 [2]。一般模式为发出的电能首先供用户自己使用，使用不完的电能可并网售卖 [3]。文献 [4] 分析了智能电网在分布式电源技术在配电网规划中的应用。此外，对于考虑地域特点随机性的规划问题，文献 [5] 基于城乡分区规划的负荷预测，提出措施促进配电网科学规划，文献 [6] 对比分析了新加坡与上海的地域随机性配电网的规划方法。文献 [7] 以无锡地区为例，梳理了地区中新能源发电的特性，讨论了对配电网规划的发展。

近年来，针对电动汽车对于规划问题影响的研究，由于乡村振兴政策，农村收入、充电条件、出行需求相符合，电费对比汽油价格相对便宜，同时家家户户独门独院，充电条件便利，同时出行需求一般为村内或村与村通行，通行距离短。对于电动汽车充电模式以及接入电网影响的研究是保障配网规划模型稳定的基础，文献 [8] 讨论了电动汽车不同充电模式的充电负荷模型。文献 [9] 考虑了一天中充电时间和次数的模拟。文献 [10] 讨论了电动汽车接入对配电网可靠性的影响。文献 [11] 讨论了电动汽车充电站选址满意度对配电网规划的影响。

且现阶段研究配电网拓展规划，较多的模型考虑了分布式电源或新能源汽车接入的一种，较少有模型同时考虑了分布式电源以及新能源的情况 [12] - [18]。配电网普遍采取解析法进行评估，但随着系统规模和复杂性的增加，计算精度和计算时间大幅增加 [19] [20] [21]。

本文中的配电网规划中考虑了分布式电源、电动汽车、主动管理措施对配电网扩建的影响。尤其是需要注意夜间的负荷模型，因为新能源车的充电多在夜间进行，与传统负荷曲线有所不同。在建模过程中，对于扩建新线路采用最小生成树方法，在电压、潮流、容量等方面设置约束，同时考虑模型的可靠性和经济性。可靠性指标以停电次数进行量化；经济性则考虑了新建投资、维护费用、运行损耗等指标。最终通过IEEE33节点系统验证了模型的有效性。

2. 新能源汽车充电负荷的处理

分布式电源和负荷的模型数据是根据不同时刻的历史数据，对其进行概率特征的提取，对比由确定公式的经验概率生成的数据更具实际参考意义。其中因为乡村电动汽车的充电方式一般为常规充电模式，即所谓的慢充模式。该种方式的充电曲线采用恒流–恒压的传统充电模式对电动车进行充电，此种充电方式在特性上和电池的固有特性基本一致，避免了电池发生欠充和过充，减少了对电池的损害。图1为恒流–恒压充电曲线。

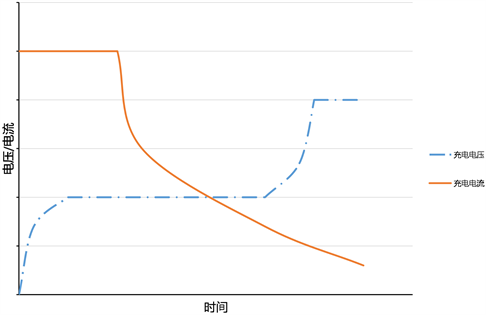
Figure 1. Constant current-constant voltage charging curve

图1. 恒流–恒压充电曲线

常规充电模式的充电电流较小，一般为0.1~0.3库伦，因为充电电流较小，所以充电时间也较长，一般为8~10小时不等。由图2可知，常规充电的开始和结束阶段相对于整个充电过程所占比例很小，可以忽略，大部分的充电过程可近似为恒功率充电。图2为实际–简化恒功率充电曲线。

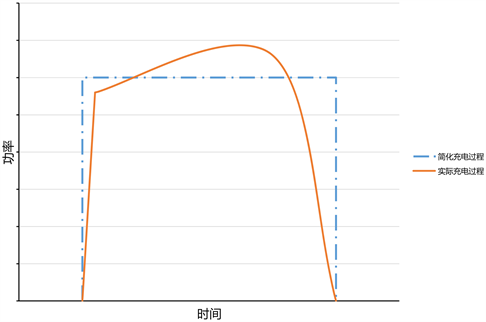
Figure 2. Real-simplified constant power charging curve

图2. 实际–简化恒功率充电曲线

假设某电动汽车充电功率为 $P_1$，其电池的起始荷电状态为 $X_1$， $X_1$ 服从正态分布 $N\left({\mu }_1,{\sigma }_1\right)$，则此辆电动车的充电时间如公式1.1所示

$T_1=\frac{E_1}{P_1}$ (1.1)

式中 $E_1$ 为此车电池待充电量，计算方法如公式1.2所示

$E_1=\left(1-X_1\right)C$ (1.2)

式中C为此车电池标称电量。

采用蒙特卡罗法随机抽取汽车电池的起始荷电 $X_1$，即可求出 $E_1$。设定汽车的充电开始时间为t，则可得到该车的充电负荷曲线。假设某一乡村内有电动汽车N辆，累加乡村内所有电动汽车的充电曲线则可得充电模型L。在选取开始充电时间t时，考虑到对传统负荷曲线起到“填谷”的作用，所以将汽车充电时段安排在负荷曲线上滑动平均值最小的时段。图3为电动汽车充电模型计算流程。

Figure 3. Calculation flow of electric vehicle charging model

图3. 电动汽车充电模型计算流程

3. 主动配电网规划中的模型与目标函数

本文构建了主动管理措施、约束经济成本、供电可靠性的量化目标函数。主动管理措施在制定恢复供电路径时，需要全面考虑新拓扑结构下下系统运行的约束，包括电压约束、潮流约束、容量约束等其它约束条件，需保证恢复供电的策略是可靠的，并且以停电次数最少为目标。

3.1. 主动管理措施

3.1.1. 容量与电压安全约束

$\{\begin{array}{ll}{V}_i^{\min }\le V_{i,\omega }\le V_i^{\max }\hfill & \forall i\in {\Theta }^n\hfill \\ V_b=1\hfill & b\in {\Theta }^{nb}\hfill \\ I_{ij}^{\min }\le I_{ij,\omega }^{\text{line}}\le I_{ij}^{\max }\hfill & \forall ij\in {\Theta }^{\text{line}}\hfill \end{array}$ (2.1)

式中： ${\Theta }^n$ 为包括原系统与待建网络的所有节点集合； ${\Theta }^{nb}$ 为平衡节点； $V_i^{\min }$ 为节点i的电压下限； $V_i^{\max }$ 为节点i的电压上限； $V_b$ 为平衡节点电压值； $V_{i,\omega }$ 为节点i在场景 $\omega$ 下的实际运行电压值； $I_{ij,\omega }^{\text{line}}$ 为线路ij在场景 $\omega$ 下的实际运行电流值。

3.1.2. 主动管理约束

$\{\begin{array}{ll}\underset{\_}{c{r}_{}^L}{P}_{i,\omega }^{L,pr}\le P_{i,\omega }^L\le P_{i,\omega }^{L,pr}\hfill & \forall i\in {\Theta }^{L,cut}\hfill \\ \underset{\_}{c{r}_{}^L}{Q}_{i,\omega }^{L,pr}\le Q_{i,\omega }^L\le Q_{i,\omega }^{L,pr}\hfill & \forall i\in {\Theta }^{L,cut}\hfill \\ \underset{\_}{c{r}_{}^{ph}}{P}_{i,\omega }^{ph,pr}\le P_{i,\omega }^{ph}\le P_{i,\omega }^{ph,pr}\hfill & \forall i\in {\Theta }^{ph}\hfill \\ \underset{\_}{c{r}_{}^w}{P}_{i,\omega }^{w,pr}\le P_{i,\omega }^w\le P_{i,\omega }^{w,pr}\hfill & \forall i\in {\Theta }^w\hfill \\ \underset{\_}{c{r}_{}^w}{Q}_{i,\omega }^{w,pr}\le Q_{i,\omega }^w\le Q_{i,\omega }^{w,pr}\hfill & \forall i\in {\Theta }^w\hfill \end{array}$ (2.2)

式中： ${\Theta }^{L,cut}$ 为参与主动管理措施的负荷点集合； $\underset{\_}{c{r}_{}^L}$ 为负荷切除的下限比例； $\underset{\_}{c{r}_{}^{ph}}$ 为光伏切除的下限比例； $\underset{\_}{c{r}_{}^w}$ 为风电功率切除的下限比例。

3.1.3. 潮流约束

$\{\begin{array}{l}{\displaystyle \underset{k:\left(j,k\right)\in {\Theta }^{\text{line}}}{\overset{}{\sum }}{P}_{jk,\omega }}={\displaystyle \underset{i:\left(i,j\right)\in {\Theta }^{\text{line}}}{\overset{}{\sum }}\left(P_{ij,\omega }-r_{\text{line},ij}\frac{P_{ij,\omega }^2+Q_{ij,\omega }^2}{V_{i,\omega }^2}\right)-P_{j,\omega }^L+P_{j,\omega }^{ss}+P_{j,\omega }^{ph}+P_{j,\omega }^w}\\ {\displaystyle \underset{k:\left(j,k\right)\in {\Theta }^{\text{line}}}{\overset{}{\sum }}{Q}_{jk,\omega }}={\displaystyle \underset{i:\left(i,j\right)\in {\Theta }^{\text{line}}}{\overset{}{\sum }}\left(Q_{ij,\omega }-x_{\text{line},ij}\frac{P_{ij,\omega }^2+Q_{ij,\omega }^2}{V_i^2}\right)-Q_{j,\omega }^L+Q_{j,\omega }^{ss}+Q_{j,\omega }^{ph}+Q_{j,\omega }^w+Q_{j,\omega }^{svc}}\\ I_{ij,\omega }^2=\left(P_{ij,\omega }^2+Q_{ij,\omega }^2\right)/V_{i,\omega }^2\forall j\in {\Theta }^n\\ V_{j,\omega }^2=V_{i,\omega }^2-2\left(r_{\text{line},ij}{P}_{ij,\omega }+x_{\text{line},ij}{Q}_{ij,\omega }\right)+\frac{\left(r_{\text{line,}ij}^2+x_{\text{line},ij}^2\right)\left(P_{ij,\omega }^2+Q_{ij,\omega }^2\right)}{V_{i,\omega }^2}\forall j\in {\Theta }^n\backslash {\Theta }^{\text{OLTC}}\\ V_{j,\omega }^2=V_{i,\omega }^2{\lambda }_{i,\omega }-2\left(r_{\text{line},ij}{P}_{ij,\omega }+x_{\text{line},ij}{Q}_{ij,\omega }\right)+\frac{\left(r_{\text{line},ij}^2+x_{\text{line},ij}^2\right)\left(P_{ij,\omega }^2+Q_{ij,\omega }^2\right)}{V_{i,\omega }^2}\forall j\in {\Theta }^{\text{OLTC}}\end{array}$ (2.3)

式中： $k:\left(j,k\right)\in {\Theta }^{\text{line}}$ 表示末节点为k的支路集合； $i:\left(i,j\right)\in {\Theta }^{\text{line}}$ 表示首节点为i的支路集合； ${\lambda }_{i,\omega }$ 为连接OLTC节点在场景下的变比； $Q_{ij,\omega }$ 为线路ij场景 $\omega$ 下的无功功率。

3.2. 供电可靠性函数

供电可靠性以停电次数最少为目标，具体目标函数表达式为：

$\min {\displaystyle \underset{\omega }{\sum }{\pi }_{\omega }{\displaystyle \underset{ij\in U}{\sum }{x}_{ij}^{line}{F}_{ij}\left(\omega \right)}}$ (2.4)

式中： $x_{ij}^{\text{line}}$ 为线路是否新建的决策变量， $F_{ij}\left(\omega \right)$ 为线路ij故障后系统在场景 $\omega$ 下的停电次数。

由式(2.4)可知，停电次数越少则该指标越优。

3.3. 经济成本函数

经济成本包括新建投资、维护费用、运行损耗。每个网架树在场景 $\omega$ 下的总费用 $C_k$ 目标函数为：

$C_k^{}\left(\omega \right)=C_{I,k}^{}+C_{M,k}^{}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{C}_{R,k}^{}\left(\omega \right)}$ (2.5)

式中： $C_{I,k}$ 为网架树 ${\Upsilon }_k$ 的投资费用； $C_{M,k}$ 为网架树 ${\Upsilon }_k$ 的维护费用； $C_{R,k}$ 为网架树 ${\Upsilon }_k$ 的运行损耗费用；T为总规划年限。

由式(2.5)可知，总费用数额越小则该指标越优。

3.4. 理想树与最优树

在本文中，对于任一概率下，所有网架树均有对应的权重值。取不同概率下不同网架树的权重值最小的值构成理想网架树，计算得出与理想网架树正弦互熵最小的网架树即为最优网架优树。图4为理想树构成示意图。

Figure 4. Schematic diagram of ideal tree composition

图4. 理想树构成示意图

在本文中取供电可靠性与每个树总费用为权重值1与权重值2，与分布概率组成三维坐标系，由此对不同树与理想树的指标进行判别衡量。

4. 算例与结果分析

4.1. IEEE33节点系统算例

使用IEEE33节点算例对本文模型及算法进行验证，见图5。算例网络结构、分布式电源安装信息、待建负荷节点、支路信息如表图、表所示。分布式电源类型为太阳能、风能发电，采用的风力强度、光照强度数据来自实际的风力发电站和光伏发电站。

功率基准值取10 MVA，电压基准值取12.66 kV。节点电压约束条件标幺值为0.95~1.05。分布式电源渗透为0.4。运行阶段的投资费用、维护费用、运行费用、等费用相关信息见表1。

Figure 5. 33-node system diagram

图5. 33节点系统图

Table 1. Bill of fare

表1. 费用清单

本程序在Matlab R2016a环境下基于CPLEX算法包进行计算，系统硬件环境为i5-3337U CPU 1.8 GHz，4 GB内存，操作系统为Win8 64bit。

4.2. IEEE33节点系统结果分析

经程序计算后输出所有网架树与理想网架树的供电可靠性权重、供电经济性权重以及分布概率的三维分布图，如图6所示。

Figure 6. Three-dimensional distribution of all trees and ideal trees

图6. 所有树与理想树三维分布图

Figure 7. Two-dimensional projection of power supply reliability weight and power supply economy weight

图7. 供电可靠性权重和供电经济性权重的二维投影

理想网架树用红色标出，综合最优网架树用绿色标出，经济最优网架树用黄色标出，可靠性最优网架树用金色标出。本文计算程序同时输出了供电可靠性权重和供电经济性权重的二维投影，如图7所示。概率分布越靠近左边，系统的可靠性越高，年停电次数越少；概率分布越靠近左边，综合成本越低。

理想网格树的概率分布在最左边因此，它具有最佳的经济性和可靠性，可以作为衡量最优规划方案的基准。网格树的分布函数越接近理想的树分布函数，相应的规划方案就越好。计算各网架树与理想网架树权重概率分布的正弦互熵，以此比较实际网架树分布与理想网架树的接近程度。