基于NTRU密文域图像可逆双水印算法的研究

Research on Image Reversible Double Watermarking Algorithm in Ciphertext Domain Based on NTRU

摘要: 本文基于NTRU密码算法对数字图像和字符串信息进行加密处理，利用NTRU密码算法的同态特性，实现不同用户在不同阶段对同一数字作品信息进行两次密文域水印信息嵌入；接收者对含水印的密文图像进行NTRU解密算法处理，能够恢复出原始作品信息和两次嵌入的水印信息。通过对比发现该算法能够完全恢复原始作品信息和嵌入的水印信息，能够达到预期效果。同时该算法基于后量子密码算法，可以对抗量子计算机的攻击，而且水印信息的嵌入量更大，能嵌入双方水印信息，嵌入和提取相互不受干扰和影响。

Abstract: In this paper, the digital image and string information are encrypted based on NTRU cryptographic algorithm. Using the homomorphic characteristics of NTRU cryptographic algorithm, different users can embed the watermark information in the ciphertext domain twice in different stages; the receiver can recover the original work information and the watermark information embedded twice by processing the ciphertext image with NTRU decryption algorithm. Through comparison, it is found that the algorithm can completely restore the original work information and embedded watermark information, and can achieve the expected effect. At the same time, the algorithm is based on post quantum cryptography algorithm, which can resist the attack of quantum computer, and the embedding amount of watermark information is larger. It can embed watermark information of both sides, and the embedding and extraction are not disturbed and affected by each other.

1. 引言

在互联网和数字媒体技术的发展下，我们的生活处处离不开数字技术，我们可以随时随地享有数字技术发展带来的方便。但与此同时也带来了新的问题和风险：数字信息在传播过程中容易被不法分子复制、篡改、恶意传播等，进而侵害个人、企业的合法权益，损害数字信息作品创作氛围，造成大量损失。所以数字信息版权保护问题迫切需要一种方案来解决。

在数字水印方面，传统的数字水印算法通常将载体图像变换到相应的频域空间，将水印信息对应嵌入在图像频域中，其中文献 [1] 中傅楚君等人提出了一种基于DCT变换的数字水印算法。文献 [2] 中胡坤等人提出了一种基于BEMD与DCT的彩色图像多重水印鲁棒算法。也有直接在空域直接进行水印信息嵌入操作，如文献 [3] 中王东东等人对LSB数字水印算法进行了研究与实现，其水印嵌入和提取效果也比较好，但算法的安全性不高，因此需要结合其他加密算法对待嵌入水印进行加解密，以此来提高水印信息的安全性。针对上述问题，文献 [4] 中Zhang等人较早地将加密技术和数字水印技术进行结合，设计出了一种在加密域进行数字水印信息嵌入的算法。而近些年得益于同态密码算法的发展，文献 [5] 中Chen等人提出在加密域应用公钥密码体制实现可逆数据隐藏方案，利用Paillier同态加密算法的同态性，将1bit的数据嵌入到两两一组的加密像素值中，解密方利用同态性质提取秘密信息。文献 [6] 中柯彦等人提出了一种基于R-LWE (ring-learning with errors)加密系统的可逆数据隐藏方案，利用多项式环上的冗余空间进行大容量数据嵌入。文献 [7] 中周能等人使用NTRU加密系统实现加密域可逆数据隐藏，其中预处理采用的算法是差值扩展算法，数据隐藏利用了NTRU加密系统同态加法的性质，但是该方案在加密域平均嵌入率较低。文献 [8] 中Zhou等人提出了一种经NTRU加密后的对密文图像进行数据隐藏的算法，加密前对明文图像进行分组，计算组内参考点与相邻点的差值，通过建立差值直方图的方法确定隐藏像素点，利用NTRU加密系统的同态加性完成数据嵌入，可实现解密前和解密后都可以提取数据。文献 [9] 中项世军等人首次提出同态加密域图像可逆水印算法。

在同态加密算法方面，当前被广泛使用的同态加密算法包括Paillier同态加密 [10]、BGV同态加密 [11] [12]、BFV同态加密 [13]、NTRU同态加密 [14] 等。其中NTRU同态密码算法相比于其他同态密码算法具有结构简洁、计算速度较快、尺寸较小等优点，因此比较适合应用于数字水印算法。

综合上述分析，将数字水印算法和同态加密算法相结合是当前数字水印研究领域的热点。当前大部分水印方案是将传统加密技术和数字水印结合，虽然能提高数字水印嵌入提取的安全性，但是由于加密算法本身的特性不便于进行第二次水印的嵌入，且加密和嵌入数据时运算开销较大，导致嵌入大量数据时程序运行时间较长。另外，随着量子计算的发展，传统加密算法能否抵抗量子计算攻击也是加密域可逆数据数字水印领域备受讨论的问题。NTRU加密系统被认为是可抵抗量子计算攻击的一种同态加密系统，且具有公私钥生成速度快、加解密运算速度快等特点，基于NTRU加密系统的可逆数字水印算法运算时间明显优于其它同态加密系统 [15]。

本文基于NTRU同态密码算法提出了一种可逆双方水印算法，该算法不同于传统的数字水印算法，首先图像信息所有者通过NTRU同态密码算法的加密算法对嵌入第一段水印的图像信息进行加密并上传至云端管理员处。云端管理员通过NTRU同态密码算法的同态特性进行第二次水印信息嵌入。最后水印信息验证者可以通过NTRU解密算法提取原始图像信息和两次嵌入的水印信息。本方案优点在于算法安全性较高，算法运行时间较短，且扩展性也比较好，可根据需要多次嵌入数字水印信息。经过实验证明，该算法解密恢复原始信息的效果比较好，能够完全恢复出原始图像和两次嵌入的水印信息。

本文的整体结构安排如下：

第2节：NTRU算法及同态特性分析；

第3节：基于NTRU密文域多方水印算法设计；

第4节：实验与分析；

第5节：总结。

2. NTRU算法及同态特性分析

2.1. NTRU算法

NTRU加密系统最早由三位数学家Jill Pipher，Jeffrey Hoffstein，Joseph Silverman提出 [14]。这种加密系统的数学核心是多项式环截断环，加密系统的可靠性由格上最短向量问题和最近向量问题保证，这属于NP难(non-deterministic polynomial hard)问题。由于加密和解密过程中只运用到简单的模乘与加减运算，在相同安全性等级的前提下，NTRU比目前现有的公钥密码系统运算更快，效率更高，具有很广阔的应用前景。

2.1.1. NTRU密码体制及其基本运算操作

NTRU算法定义在多项式环上，R上的元素——多项式 $f\left(x\right)$ 也可以用向量表达： $f={\displaystyle {\sum }_{i=0}^{N-1}{f}_i\cdot x^i}=\left[f_0,f_1,\cdots ,f_{N-1}\right]$。对于环中的任意两个多项式 $f\left(x\right)$ 和 $g\left(x\right)$ 可以表示为以下的形式： $f=f_0+f_1\cdot x+\cdots +f_{N-1}\cdot x^{N-1}$， $g=g_0+g_1\cdot x+\cdots +g_{N-1}\cdot x^{N-1}$。元素之间存在多种运算，包括：

系数乘法操作：对于任意实数 $k\in R$，满足 $k\cdot f\left(x\right)=k\cdot f_0+k\cdot f_1\cdot x+\cdots +k\cdot f_{N-1}\cdot x^{N-1}$

多项式加法操作：对于两个多项式截断环f和g之间的加法定义如下：

$f\left(x\right)+g\left(x\right)={\displaystyle {\sum }_{i=0}^{N-1}\left(f_i+g_i\right)\cdot x^i}$ (2-2)

多项式乘法操作：对于两个多项式截断环f和g之间的乘法(星乘)定义如下：

$f\left(x\right)\ast g\left(x\right)={\displaystyle {\sum }_{i=0}^{N-1}\left({\displaystyle {\sum }_{i+j=k\left(\mathrm{mod}N\right)}{f}_i\cdot g_j}\right)\cdot x^i}$ (2-3)

2.1.2. NTRU加解密参数

NTRU密码体制由3个正整数 $\left(N,p,q\right)$ 和4个整系数多项式集合 $L_f,L_g,L_r$ 和 $L_m$ 共同决定。其中正整数p和q的选取满足 $\gcd \left(p,q\right)=1$ 且q远大于p。用“*”乘表示环R中的乘法，在整个密码系统中，一部分乘法将在模q下运算，另一部分将在模p下运算。多项式 $L_f,L_g,L_r$ 和 $L_m$ 的选取应遵循以下原则：明文m所选取的集合 $L_m$ 是包括所有模p的多项式。这里为了方便讨论，假设p是奇数，于是有

$L_m=\left\{m\in R:m的系数位于-\frac{p-1}{2}和\frac{p-1}{2}之间\right\}$。

另外3个多项式集合均采用如下形式：

$L\left(d_1,d_2\right)=\left\{F\in R:F中有d_1个系数等于1,d_2个系数等于-1,剩下的系数为0\right\}$

因此，3个正整数 $d_f,d_g$ 和 $d_r$ 便可确定参数选取集合： $L_f=L\left(d_f,d_f-1\right)$， $L_g=L\left(d_g,d_g\right)$， $L_r=L\left(d_r,d_r\right)$。

2.1.3. NTRU算法加密解密过程

首先根据参数 $d_f$ 生成多项式f，其必须满足f模p的逆 $f_p^{-1}$ 和f模q的 $f_q^{-1}$ 逆存在，否则重新生成f。然后计算 $f_p^{-1}$ 和 $f_q^{-1}$。最后根据参数 $d_g$ 生成多项式g。根据公式(2-4)计算多项式h: $h=p\cdot F_q\ast g\left(\mathrm{mod}q\right)$。当计算全部完成后，可得到公钥为 $K_{pub}=h$，私钥为 $K_{pri}=\left(f,f_p\right)$。

加密过程：是在加密数据信息前需要将数据信息编码为明文多项式，使其每个系数的范围为 $\left[-\frac{p}{2},\frac{p}{2}\right]$，

如当 $p=3$ 时，明文多项式m的系数范围是 $\left\{-1,0,1\right\}$。获取公钥h后，即可对明文多项式 $m\in L_m$ 进行加密，随机选取噪声多项式 $r\in L_r$，对明文m根据以下公式操作得到密文多项式e： $e=r\ast h+m\left(\mathrm{mod}q\right)$。

解密过程：给定密文多项式e和私钥 $\left(f,f_p\right)$ 可以解密得到明文多项式m。首先根据公式 $a=f\ast e\left(\mathrm{mod}q\right)$ 计算中间多项式a。然后根据公式 $c=F_p\ast a\left(\mathrm{mod}p\right)$ 计算得到解密后的明文多项式c。最后再根据明文编码规则进行逆编码即可得到明文数据data。

2.1.4. NTRU安全等级

Silverman等人给出了NTRU不同的参数选取方案，以此来获得不同的安全等级。在NTRU公钥密码的原始方案中，N = 107规模的参数对应了中等安全性密码系统。表1是NTRU-1998参数集对应的安全性等级 [14]。

Table 1. Recommended parameters for different security levels of NTRU

表1. NTRU不同安全性等级的推荐参数

2.2. NTRU同态性质

NTRU存在加法同态性：对于任意的两个明文多项式 $m_1$ 和 $m_2$，选择两个随机的多项式 $r_1$ 和 $r_2$，则经过加密之后对应生成的密文为 $e_1$ 和 $e_2$，其中满足：

密文相加时： $e_1+e_2=\left(r_1+r_2\right)\ast h+m_1+m_2\left(\mathrm{mod}q\right)$

解密时： $Dec\left(e_1+e_2\right)=m_1+m_2\left(\mathrm{mod}q\right)$

即两个密文多项式的之和在解密后等于对应的两个明文多项式之和：

假设明文 $P{T}^{\prime }={\displaystyle {\sum }_{i=0}^{N-1}p{t^{\prime }}_i\cdot x^i}=\left[p{t^{\prime }}_0,p{t^{\prime }}_1,\cdots ,p{t^{\prime }}_{N-2},p{t^{\prime }}_{N-1}\right]$ ；

明文 $P{T}^{″}={\displaystyle {\sum }_{i=0}^{N-1}p{t^{″}}_1\cdot x^i}=\left[p{t^{″}}_0,p{t^{″}}_1,\cdots ,p{t^{″}}_{N-2},p{t^{″}}_{N-1}\right]$ ；

经过NTRU加密后分别得到：

密文 $C{T}^{\prime }={\displaystyle {\sum }_{i=0}^{N-1}c{t^{\prime }}_i\cdot x^i}=\left[c{t^{\prime }}_0,c{t^{\prime }}_1,\cdots ,c{t^{\prime }}_{N-2},c{t^{\prime }}_{N-1}\right]$ ；

密文 $C{T}^{″}={\displaystyle {\sum }_{i=0}^{N-1}c{t^{″}}_i\cdot x^i}=\left[c{t^{″}}_0,c{t^{″}}_1,\cdots ,c{t^{″}}_{N-2},c{t^{″}}_{N-1}\right]$ ；

同态加操作： $C{T}^{*}={\displaystyle {\sum }_{i=0}^{N-1}\left(c{t^{\prime }}_i+c{t^{″}}_i\right)\cdot x^i=\left[c{t^{\prime }}_0+c{t^{″}}_0,c{t^{\prime }}_1+c{t^{″}}_1,\cdots ,c{t^{\prime }}_{N-2}+c{t^{″}}_{N-2},c{t^{\prime }}_{N-1}+c{t^{″}}_{N-1}\right]}$ ；

对密文 $C{T}^{*}$ 解密后得到明文结果如下：

$P{T}^{*}={\displaystyle {\sum }_{i=0}^{N-1}\left(p{t^{\prime }}_i+p{t^{″}}_i\right)\cdot x^i=\left[p{t^{\prime }}_0+p{t^{″}}_0,p{t^{\prime }}_1+p{t^{″}}_1,\cdots ,p{t^{\prime }}_{N-2}+p{t^{″}}_{N-2},p{t^{\prime }}_{N-1}+p{t^{″}}_{N-1}\right]}$

3. 双水印算法设计

本文提出的方案充分利用NTRU加密系统的多项式空间冗余性以及NTRU加密的同态性。原始信息所有者将原始信息加密后将得到一些密文多项式，其他用户可以在不同阶段将密态信息嵌入到密文多项式中。掌握私钥的用户则可以对密文解密，解密后将获取原始信息和其他用户嵌入的信息。

3.1. 算法流程

本文提出了一种基于NTRU的密文域双方数字水印算法，该算法主要由四部分构成：原始图像信息和字符串水印信息加密、图像水印信息加密、第二段水印信息嵌入、解密提取原始图像和双水印信息。

本算法包括图像作品拥有者A、云端管理者B和水印信息验证者C三种用户。

第一步：图像作品拥有者A嵌入字符串水印信息并加密图像，得到含水印密文图像P₁；

第二步：云端管理员B加密水印图像，得到密文水印图像P₂；

第三步：云端管理员B向含水印密文图像P₁嵌入第二段水印信息P₂；

第四步：水印信息验证者C双水印验证者C解密密文图像并提取原始图像和先后嵌入的两段水印信息。

方案流程图如图1所示。

3.2. 信息编码与加密解密

3.2.1. 字符串信息编码

对于字符串类型的数据，要将其每一个字符都编码成8比特(1个字节)的二进制形式，然后按顺序依次填充到多项式对应的系数上，构造出相应的明文多项式。

3.2.2. 图像信息编码

在数字图像中，一个点通常用像素来表示，一个字节包含8个比特，每个比特可以表示为1或者0。在简单的二值图像中一个像素点由一个字节来表示。而复杂一些的图像(例如24位真彩色BMP)，一个像素由三个字节构成，每个字节分别表示256种状态的红、绿、蓝。本算法针对彩色图像进行信息加密，因此在编码明文多项式时，需要将像素点转化为二进制字符串并填充到明文多项式对应系数上。

3.2.3. 加密明文多项式

图片或字符串信息经过编码后得到若干个明文多项式，对每一段明文多项式执行NTRU加密算法后将得到对应的密文多项式。

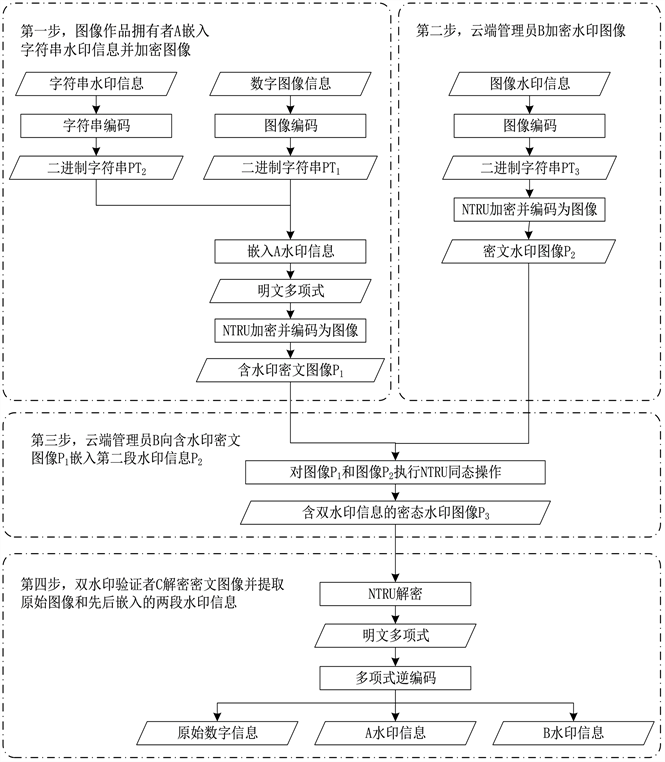
Figure 1. Flowchart of double watermarking algorithm in ciphertext domain based on NTRU

图1. 基于NTRU密文域双水印算法的流程图

3.2.4. 解密密文多项式

解密方得到密文多项式后，使用私钥对其执行NTRU解密算法。以中等安全系数(N = 167)为例，对于解密后得到的每一段明文多项式，都由三部分组成：前96个系数代表原始数字图像的4个像素信息、中间32个系数代表第一段水印信息(字符串)、之后的24个系数代表第二段水印信息(图像)的1个像素信息。将这些信息按照3.2.1节中的编码格式进行还原可以得到原始图像信息和水印信息(包括字符串和图像水印信息)。

3.3. 具体过程

以中等安全等级(N = 167)为例，每个多项式有167个系数可以嵌入数据。

3.3.1. 图像作品拥有者A嵌入字符串水印信息并加密图像

首先图像作品拥有者A对原始数字图像信息进行编码，每4个像素点为一组，构造出长度为96的二进制字符串。从多项式的第1个系数开始，将96个二进制数依次置入明文多项式(不足4个像素点则需要填充0)。经过处理后，每四个像素点信息都将产生一个多项式形式的明文。然后将字符串水印信息也编码为二进制字符串，每4个字符(32比特)为一组，从明文多项式的第97个系数到第128个系数依次置入二进制字符串信息。其他字符串信息以同样的方式依次置入下一个明文多项式。鉴于原始图像的像素信息比较多，因此能够构造出多个明文多项式，对于每个明文多项式具体填充形式如图2所示。

Figure 2. Schematic diagram of encoding original image and string watermark information

图2. 对原始图像和字符串水印信息编码示意图

之后对每个明文 $P{T}_i$ 都经过NTRU密码算法加密，每个明文 $P{T}_i$ 都将产生对应的密文 $C{T}_i$，每个密文也是以多项式的形式表达，如图3所示。最后将得到的密文编码为图像信息并发送给云端管理员B。

Figure 3. Schematic diagram of ciphertext polynomial

图3. 密文多项式示意图

每个多项式除前128位外，剩余的位置均未置入其他有效信息，多项式系数具有一定的冗余度。云端管理员B将在冗余的系数上嵌入第二段水印信息(图像水印)。

3.3.2. 云端管理员B加密水印图像

云端管理员需要将每个明文多项式的前128位置为0，水印图像的信息将嵌入在多项式中剩余的位置上。将水印图像的每个像素点信息(24位)编码成以二进制形式表示的字符串，每个明文多项式从第129位开始置入像素信息。对图片的所有像素信息采用同样的处理后将构造出多个多项式形式的明文。对于一个具体的明文，其填充方式如图4所示。

Figure 4. Constructing plaintext polynomial of watermark image in cloud

图4. 云端构造水印图像的明文多项式

之后对每组明文执行NTRU密码算法加密，每个明文都将产生对应的密文 $C{T^{\prime }}_i$。最后将得到的密文编码为图像信息。

3.3.3. 云端管理员B嵌入第二段水印信息

云端管理员B此时持有来自双方的密文图像信息，下一步将同态地处理密文图像信息，进而计算得到带有原始图像、字符串水印和图片水印的密文图像，如图5。具体操作是将密文多项式进行同态加法运算，即 $C{T}_i^{\ast }=C{T}_i+C{T^{\prime }}_i$。

Figure 5. The cloud administrator performs homomorphic addition on ciphertext

图5. 云端管理员对密文执行同态相加操作

3.3.4. 水印信息验证者C解密提取原始图像和双水印信息

水印信息验证者C从密文图像中提取密文并进行解密后，将得到对应的明文，每个明文多项式系数的前24位为原始图像像素信息，第25位到第72位为字符串水印信息，剩余的系数为云端管理员嵌入的图像水印信息(每24比特表示一个像素信息)，具体结构如图6。根据原来的编码方式进行逆编码，我们将还原出原始图像信息、字符串水印信息和图像水印信息。

Figure 6. The decryptor provides the private key for decryption

图6. 解密方提供私钥进行解密

4. 实验与分析

4.1. 实验过程

本文首先以彩色Lena图像(如图7所示)作为原始图像、原始图像的摘要值(MD5)作为字符串水印和彩色“数字水印”图像(如图8所示)作为水印图像进行实验。其中彩色Lena图像的像素大小为256 * 256；字符串水印信息为该Lena图像的MD5值：27bf9f58bd64ad14c76345c5ec771b19，彩色BIGC图像的像素大小为50 * 50。

Figure 7. Original image information

图7. 原始图像信息

Figure 8. Image watermark information

图8. 图像水印信息

实验中采取最高安全性等级(N = 503)参数进行实验，实验中原始图像信息经NTRU加密算法，产生了3450组密文多项式，将这些密文多项式编码为数字图像信息后得到含字符串水印的密文图像P₁ (如图9(a))。云端管理员加密数字水印图像信息产生了2500组密文多项式。同样地将这些密文多项式编码为数字图像信息后得到图像水印的密文图像P₂ (如图9(b))。对这两个密文图像进行NTRU同态相加操作，得到含双水印信息的密文图像P₃ (如图9(c))。

(a) (b) (c)

Figure 9. (a) Ciphertext Image P₁; Ciphertext Image P₂; Ciphertext Image P₃

图9. (a) 密文图像P₁；(b) 密文图像P₂；(c) 密文图像P₃

对经过同态求和算法得到的含有双方水印信息的密文图像P₃进行直方图统计(如图10)可以看出每个像素点的分布服从较好的随机分布，因此该算法具有较好的安全性。

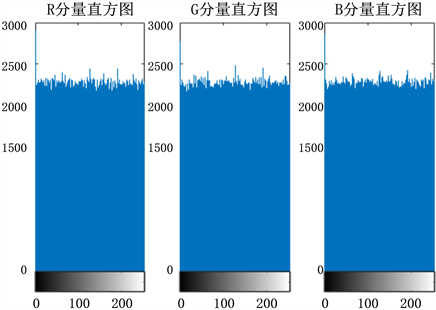
Figure 10. Histogram statistical results of watermark image containing both watermark information

图10. 含双方水印信息的水印图像的直方图统计结果

密文信息解密和信息提取阶段：

解密时，需要先将密文图像编码为相应的密文多项式。对这些密文多项式执行NTRU解密算法，最终得到3450组包含原始图像信息、字符串水印信息、图像水印信息的明文多项式。再对其进行逆编码，将恢复出原始图像信息(如图11所示)、字符串水印信息(27bf9f58bd64ad14c76345c5ec771b19)、图像水印信息(如图12所示)。

Figure 11. Recover the original image information after decryption

图11. 解密后还原得到的原始图像信息

Figure 12. Recover the image watermark information after decryption

图12. 解密后还原得到的图像水印信息

经比较，解密恢复得到的字符串水印信息与原字符串水印信息一致，解密恢复得到的图像信息和图像水印信息与原始图像一致。对原始图像和解密恢复得到的图像进行PSNR对比，结果显示经过该算法并解密后得到图像信息与原来的图像信息完全一致，因此该算法能够完全恢复原始图像和水印信息。

4.2. 运行效率

经实验测试得到对编码后的2048个明文多项式执行2048次NTRU加密运行时间、解密运算时间、同时执行加解密和文件编码解码所需要总的时间开销如表2所示：

Table 2. Time cost of encrypting and decrypting 2048 polynomials under different security levels of NTRU

表2. NTRU不同安全性等级下对2048个多项式进行加解密时间开销

通过实验分析可以看出，进行合理的参数选择和多项式系数分配将有效利用明文多项式的系数，进而减少因构造多项式过多带来空间和时间上的开销，提高运行效率。当选择最高安全性等级时，虽然单次加解密时间是最长的，但是一次可以填充多个系数，加解密所需要的空间开销和时间开销是最低的。

4.3. 安全性分析

本方案是基于NTRU加密算法实现的，文献 [15] 证明了NTRU算法的正确性和安全性，其安全性可规约到格上SVP (Shortest Vector Problem)问题 [16] 和BDD (Bounded Distance Decoding)问题 [17]。同时在标准模型下是IND-CPA(选择明文攻击下的不可区性)安全的 [18]。

原始图像所有者和云管理员都需要对嵌入信息进行NTRU加密算法加密，任意阶段产生的密态水印信息——密文多项式都需要NTRU私钥进行解密后才能提取原始信息，因此该方案具有等价于NTRU加密系统的安全性。通过对比NTRU、RSA和ECC三种公钥密码体制之间的安全级别 [14]，NTRU在相同安全性等级下密钥都短于另外两种公钥密码体制，同时其加解密速度也优于另外两种公钥密码体制。进行暴力破解攻击时，随着N的增大，因花费时间太长而基本不能破解 [14]。因此，NTRU加密体制能够提供足够的安全性能。

5. 总结

本文提出了一种基于NTRU密文域图像可逆双水印算法，该算法不同于传统的水印嵌算法嵌入提取以及密文的存储形式都是在多项式上进行。图像作品拥有者加密图像和字符串水印信息后，云端管理员可以随时将图片水印信息加密后嵌入到用户上传的密文多项式中，持有私钥的双水印信息验证者在对密文多项式解密后将得到原始图像、字符串水印信息、图片水印信息。同时，本方案可以根据不同环境需要，对明文多项式信息嵌入位置进行进一步设计，可以嵌入更多次水印信息，具有很好的扩展性。

与传统的水印信息嵌入提取算法相比，该算法综合嵌入率较高，并且多项式系数位嵌入时具有较高的灵活性。相比于其他后量子密码算法具有密钥长度短、执行速度快、安全强度高等优点。

但由于NTRU加密系统本身固有的小概率解密失败的问题，可能会造成图像水印信息中个别像素点不能正确恢复的情况发生。因此需要进一步研究NTRU解密算法的准确性问题，以提高本方案的准确性。

基金项目

国家自然科学基金(61370188)；北京市教委科研计划(KM202010015009)；北京市教委科研计划资助(No. KM202110015004)；北京印刷学院博士启动金项目(27170120003/020)；北京印刷学院科研创新团队项目(Eb202101)；北京印刷学院校内学科建设项目(21090121021)；北京印刷学院重点教改项目(22150121033/009)；北京印刷学院科研基础研究一般项目(Ec202201)。