基于改进Klausmeier模型的交叉对流对斑图形成的影响研究

Research on the Effects of Cross-Advection on Pattern Formation Based on Modified Klausmeier Model

摘要: 为了研究交叉对流项对斑图形成的影响，将缓坡上植被种子随水流动的效应，通过交叉对流项引入一个改进的Klausmeier模型。对模型进行无量纲化后，求解了其空间均匀定态解以及稳定性。基于稳定的均匀定态解，进行了图灵分岔分析，揭示交叉对流项对图灵分岔的影响。使用分岔图和斑图形成的模拟，验证理论分析的结果。结果显示，交叉对流项使得系统发生分岔的难度改变，使得系统形成稳定带状斑图的速度更快，但形成的植被带移动速度降低。

Abstract: In order to investigate the effects of cross-advection on pattern formation, the effects of vegetation seed dispersal along with hillslope runoff were considered as a cross-advection term in a modified Klausmeier model. After the nondimensionalization of the model, its spatially homogeneous steady states of the model and the corresponding stability are solved. Based on the stable homogeneous steady states, Turing bifurcation analysis was performed to reveal the effects of cross-advection on Turing bifurcation. Bifurcation diagram and simulation of pattern formation were obtained to verify the theoretical results. The results show that with the cross-advection, the difficulty of Turing bi-furcation occurrence varies, and the formation of stable banded patterns becomes faster, but the propagation velocity of vegetation bands decreases.

1. 引言

图灵斑图是一类重要的时空斑图 [1]。近几年，在《Science》《Nature》等顶级期刊上均有对图灵斑图的相关研究 [2] [3] [4]。植被斑图是一类典型的时空图灵斑图，也是干旱半干旱地区的一种重要景观 [5] [6]。近几十年来，干旱、半干旱地区的植被斑图形成引起了理论生态学家的广泛兴趣。研究表明，植被斑图的形成主要是由植物与水资源之间反馈作用所导致 [7] [8] [9]。对植被斑图的研究，不仅可以揭示植被斑图形成的内在机制和获得其形成的主导因素，还可以为干旱与半干旱地区制定合理的植被恢复和保护策略提供科学依据 [10]。

反应扩散模型是研究植被斑图的主要形式。基于植物与水资源之间的反馈作用机制，研究者们建立了众多的时空动力学模型，主要包括Klausmeier模型 [11]，Rierkerk模型 [12]，Gilad模型 [13] 等。很多的研究基于这些模型及改进的模型做了大量的斑图形成的探索研究 [14] [15] [16]。在这些模型中，Klausmeier 模型作为一个经典模型起着重要的作用 [11]。1999年，Klausmeier应用反应对流扩散模型研究半干旱地区坡地上的植被斑图形成 [11]。Sherratt等 [17] 提出水在缓坡上不仅有对流过程，还应具有扩散过程，因此将水的扩散项引入Klausmeier模型。实际上，在缓坡上植被种子也会随径流流动 [18]。

本研究将基于引入交叉对流项的改进Klausmeier模型，研究其空间均匀定态解及线性渐近稳定性。并基于线性渐近稳定的定态解，进行图灵分岔分析，研究交叉对流项对斑图分岔点和斑图形成的影响。然后通过分岔图、数值模拟的验证理论分析的结果，揭示交叉对流系数的改变对斑图形成的影响。

2. 引入交叉对流项的改进Klausmeier模型

Klausmeier模型 [11] 是以植物生物量和水资源量作为状态变量的时空连续动力学模型，其表达式为：

$\{\begin{array}{l}\frac{\partial V\left(x,y,t\right)}{\partial t}=RJW{V}^2-MV+D_V{\nabla }^{2}V\\ \frac{\partial W\left(x,y,t\right)}{\partial t}=A-LW-RW{V}^2-A_W\frac{\partial W}{\partial x}\end{array}$ (1)

其中， $V\left(x,y,t\right)$ 表示植被的地上生物量， $W\left(x,y,t\right)$ 表示水量。R表示植被对水分的吸收系数；J表示转换率；M表示死亡率；A表示年均降雨量；L表示蒸发损失率。Klausmeier模型基于对植物和水之间反馈作用机制基本特征的刻画，并借助图灵分岔机制，其数值模拟的结果与野外观测结果十分吻合。因此Klausmeier模型成功地揭示了干旱、半干旱地区坡地上带状植被斑图的自组织形成。

Sherratt [17] 提出水在缓坡上不仅有对流过程，还应具有扩散过程，因此将水的扩散项引入Klausmeier模型，其表达式可表示为：

$\{\begin{array}{l}\frac{\partial V\left(x,y,t\right)}{\partial t}=RJW{V}^2-MV+D_V{\nabla }^{2}V\\ \frac{\partial W\left(x,y,t\right)}{\partial t}=A-LW-RW{V}^2-A_W\frac{\partial W}{\partial x}+D_W{\nabla }^{2}W\end{array}$ (2)

其中，D_W表示水在缓坡上的扩散系数。实际上，在缓坡上植被种子也会随径流流动 [18]。因此，本研究考虑将这个过程引入上述改进的Klausmeier模型，得到一个含交叉对流项的Klausmeier模型，其表达式可表示如下：

$\{\begin{array}{l}\frac{\partial V\left(x,y,t\right)}{\partial t}=RJW{V}^2-MV-A_V\frac{\partial W}{\partial x}+D_V{\nabla }^{2}V\\ \frac{\partial W\left(x,y,t\right)}{\partial t}=A-LW-RW{V}^2-A_W\frac{\partial W}{\partial x}+D_W{\nabla }^{2}W\end{array}$ (3)

其中，A_V表示植被随水流方向的对流系数。将其无量纲化 [11] 可表示为：

$\{\begin{array}{l}\frac{\partial v\left(x,y,t\right)}{\partial t}=w{v}^2-mv-a_v\frac{\partial w}{\partial x}+{\nabla }^{2}v\\ \frac{\partial w\left(x,y,t\right)}{\partial t}=a-w-w{v}^2-a_w\frac{\partial w}{\partial x}+d_w{\nabla }^{2}w\end{array}$ (4)

3. 空间均匀定态解及稳定性

考虑方程组(4)等于0时，得到的解为模型的空间均匀定态解。容易看出，空间均匀定态解的求解过程等价于相应时间模型的平衡点解。因此，可通过以下方程组来求解不动点：

$\{\begin{array}{l}w{v}^2-mv=0\\ a-w-w{v}^2=0\end{array}$ (5)

解之得，当 $a>2m$ 时，系统存在以下三个平衡点：

$\left(v_0,w_0\right)=\left(0,a\right)$ (6a)

$\left(v_1,w_1\right)=\left(\frac{a+\sqrt{a^2-4m^2}}{2m},\frac{2m^2}{a+\sqrt{a^2-4m^2}}\right)$ (6b)

$\left(v_2,w_2\right)=\left(\frac{a-\sqrt{a^2-4m^2}}{2m},\frac{2m^2}{a-\sqrt{a^2-4m^2}}\right)$ (6c)

每个平衡点都表示该系统的一个空间均匀定态。其中 $\left(v_0,w_0\right)$ 里 $v=0$，为边界平衡点。 $\left(v_1,w_1\right)$ 和 $\left(v_2,w_2\right)$ 为内平衡点。平衡点的线性渐近稳定性(局部)可以由其雅可比矩阵的特征值来进行研究。模型的雅可比矩阵可表示为：

$J=\left(\begin{array}{cc}2wv-m& v^2\\ -2wv& -1-v^2\end{array}\right)$ (7)

将内平衡点分别代入上述雅可比矩阵中，并求出对应的特征值。稳定不动点对应的矩阵特征值应满足特征值实部的最大值小于0。通过简单地分析可知平衡点 $\left(v_2,w_2\right)$ 总是线性渐近稳定的，其对应的特征值分别为：

${\lambda }_1=\frac{\frac{2a\left(a-\sqrt{a^2-4m^2}\right)}{4m^2}+m+\sqrt{\Delta }}{2}$， ${\lambda }_2=\frac{\frac{2a\left(a-\sqrt{a^2-4m^2}\right)}{4m^2}+m-\sqrt{\Delta }}{2}$ (8)

其中，

$\Delta =\frac{a^2\left(a^2-2m^2-a\sqrt{a^2-4m^2}\right)}{2m^4}+m^2-\frac{\left(a-\sqrt{a^2-4m^2}\right)\left(2\sqrt{a^2-4m^2}-3a\right)}{m}$ (9)

而平衡点 $\left(v_1,w_1\right)$ 是线性渐近稳定的条件为 $m\le 2$，其对应的特征值为：

${\lambda }_1=\frac{-\frac{2a\left(a+\sqrt{a^2-4m^2}\right)}{4m^2}+m+\sqrt{\Delta }}{2}$， ${\lambda }_2=\frac{-\frac{2a\left(a+\sqrt{a^2-4m^2}\right)}{4m^2}+m-\sqrt{\Delta }}{2}$ (10)

其中，

$\Delta =\frac{a^2\left(a^2-2m^2+2a\sqrt{a^2-4m^2}\right)}{2m^4}+m^2-\frac{\left(a+\sqrt{a^2-4m^2}\right)\left(2\sqrt{a^2-4m^2}-a\right)}{m}$ (11)

4. 图灵分岔分析

图灵分岔分析将在总是线性渐近稳定的内平衡点 $\left(v_2,w_2\right)$，即整个模型稳定的空间均匀定态解 $\left(v_2\left(x,y,t\right),w_2\left(x,y,t\right)\right)$ 处进行。对 $\left(v_2\left(x,y,t\right),w_2\left(x,y,t\right)\right)$ 进行空间非均匀的扰动：

$v\left(x,y,t\right)=v_e+\epsilon \left(x,y,t\right)$ (12a)

$w\left(x,y,t\right)=w_e+\theta \left(x,y,t\right)$ (12b)

其中 $\epsilon \left(x,y,t\right)$， $\theta \left(x,y,t\right)$ 表示在t时刻空间斑块 $\left(x,y\right)$ 上的扰动变量。将上式代入原方程组，并进行线性化得到：

$\{\begin{array}{l}\frac{\partial \epsilon \left(x,y,t\right)}{\partial t}=a_{11}\epsilon +a_{12}\theta -a_v\frac{\partial \theta }{\partial x}+{\nabla }^2\epsilon \\ \frac{\partial \theta \left(x,y,t\right)}{\partial t}=a_{21}\epsilon +a_{22}\theta +a_w\frac{\partial \theta }{\partial x}+d_w{\nabla }^2\theta \end{array}$ (13)

令

$\epsilon \left(x,y,t\right)=\bar{\epsilon }\left(t\right){\text{e}}^{i\left(l_{1}x+l_{2}y\right)}$， $\theta \left(x,y,t\right)=\bar{\theta }\left(t\right){\text{e}}^{i\left(l_{1}x+l_{2}y\right)}$ (14)

代入上式可得：

$\{\begin{array}{l}\frac{\partial \bar{\epsilon }\left(x,y,t\right)}{\partial t}=a_{11}\bar{\epsilon }+a_{12}\bar{\theta }-a_v\bar{\theta }{l}_{1}i+\bar{\epsilon }\left(l_1^2+l_2^2\right)i^2\\ \frac{\partial \bar{\theta }\left(x,y,t\right)}{\partial t}=a_{21}\bar{\epsilon }+a_{22}\bar{\theta }-a_w\bar{\theta }{l}_{1}i+d_w\bar{\theta }\left(l_1^2+l_2^2\right)i^2\end{array}$ (15)

其中，

$a_{11}=2wv-m,a_{12}=v^2,a_{21}=-2wv,a_{22}=-1-v^2$ (16)

此方程组的雅克比矩阵可写为：

$J=\left(\begin{array}{cc}{a}_{11}-\left(l_1^2+l_2^2\right)& a_{12}-a_v{l}_{1}i\\ a_{21}& a_{22}-a_w{l}_{1}i-d_w\left(l_1^2+l_2^2\right)\end{array}\right)$ (17)

可以看到，交叉扩散项的对系统动力学的影响，体现在它影响了雅可比矩阵的非对角线元素。计算此矩阵的两个特征值为：

$\begin{array}{l}{\lambda }_{1,2}=\frac{1}{2}\left(a_{11}+a_{22}-\left(l_1^2+l_2^2\right)\left(1+d_w\right)-a_w{l}_{1}i\right)\\ \pm \frac{1}{2}\sqrt{{\left(a_{11}-a_{22}+a_w{l}_{1}i-\left(l_1^2+l_2^2\right)\left(1+d_w\right)\right)}^2+4a_{21}\left(a_{12}-a_v{l}_{1}i\right)}\end{array}$ (18)

其实部的最大值为：

$\max \left(\mathrm{Re}\left(\lambda \right)\right)=\frac{1}{2}\left(P+\frac{\phi +\sqrt{{\phi }^2+{\psi }^2}}{2}\right)$ (19)

其中，

$P=a_{11}+a_{22}-\left(l_1^2+l_2^2\right)\left(1+d_w\right)$ (20a)

$\phi ={\left(a_{11}-a_{22}-\left(l_1^2+l_2^2\right)\left(1+d_w\right)\right)}^2-a_w^2{l}_1^2+4a_{12}{a}_{21}$ (20b)

$\psi =2a_w{l}_1{\left(a_{11}-a_{22}-\left(l_1^2+l_2^2\right)\left(1+d_w\right)\right)}^2-4a_{21}{a}_v{l}_1$ (20c)

图灵分岔理论表明，当 $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 等于0为系统的分岔点；当 $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 大于0时，系统发生图灵分岔，即

$\frac{1}{2}\left(P+\frac{\phi +\sqrt{{\phi }^2+{\psi }^2}}{2}\right)>0$ (21)

5. 数值模拟

本部分进行数值模拟以展示交叉对流项对半干旱地区植被斑图分岔点及对斑图形成的影响。我们通过改变参数并分析色散图，发现交叉对流项影响了特征值的分岔点，从而影响了系统的斑图形成。参数a、m以及 $d_v$ 的取值保持不变： $a=2$， $m=0.45$， $d_w=50$。

5.1. 交叉对流对分岔点的影响

假设在x和y方向的扰动是相等的。考虑交叉对流项存在和不存在两种情况，做图灵分岔的分岔图。由图1(a)可以看出，当没有交叉对流项 $a_v\frac{\partial w}{\partial x}$，即 $a_v=0$ 时， $a_w=30$ 时，特征值实部的最大值 $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 恒小于0，表明不能发生图灵分岔。而当 $a_w=67.5$ 时， $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 的最大值等于0；这表明 $a_w=67.5$ 为系统的图灵分岔点，当 $a_w>67.5$ 时，系统发生图灵分岔。如 $a_w=190$ 时， $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 明显有一部分是大于0的。

下面考虑 $a_w=30$， $a_v\ne 0$ 的情况。由图1(b)可以看出， $a_v$ 的增大可以使得 $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 的最大值变大，从而使得系统发生图灵分岔。此时，图灵分岔的分岔点为 $a_v=35.5$ ；当 $a_v>35.5$ 时，系统发生图灵分岔。比较图1(a)中的红线和图1(b)中的红线可知， $a_v$ 的存在，使得系统发生图灵分岔所需的 $a_w$ 减小了(从67.5减小为30)。

实际上，在x和y方向的扰动是不同的，特征值实部的最大值 $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 的变化由图1(c)和图1(d)给出。从图中可以看出，即使考虑扰动的各向异性， $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 的最大值依然出现在 $l_1$ 轴上( $l_2=0$ )。这表明斑图的振幅将只会出现在平行于x的方向上；这意味着模拟将得到带状的植被斑图。注意，此时我们将 $l_1$ 的方向设置为x方向。通过对比图1(c)和图1(d)，可以看出 $a_v$ 的变化稍稍增大了 $\max \left(\mathrm{Re}\left(\lambda \right)\right)$ 的最大值。但这个变化不是特别明显，因此我们需要通过斑图形成的数值模拟来进一步研究和验证。

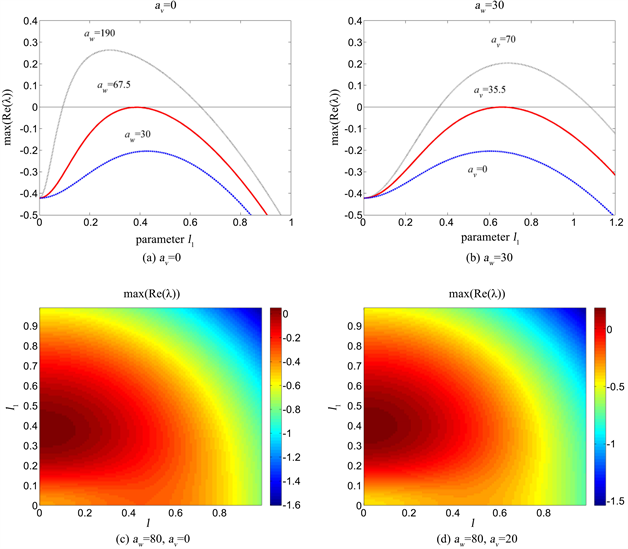
Figure 1. Variations of the maximum of real part of eigenvalues with perturbation number k in different cases of parameter values

图1. 特征值实部最大值在不同参数取值下随扰动模数k的变化曲线

5.2. 交叉对流对斑图形成的影响

数值模拟在100 × 100的方格上进行，初值设定为对空间均匀定态解进行非均匀随机扰动，同时采用周期性边界条件，通过有限差分法进行迭代模拟。同时，参数 $a_w$ 固定取值为30。图2展示了植被从空间均匀定态解，经扰动后(图2(a)和图2(b))，逐渐退化形成带状植被斑图的过程；主要包括4个不同时刻的植被生物量的空间分布，即 $t=0$， $t=5$， $t=15$ 和 $t=100$。注意，对应图1(c)和图1(d)，斑图中我们将竖直方向设置为x方向(坡向)，将水平方向设置为y方向。

当 $a_v=0$ 时，在 $t=5$ 时，植被的斑块已经开始形成(图2(c))。到 $t=15$ 时，小斑块间聚合形成较大的斑块，并有部分呈带状分布(图2(e))。当 $t=100$ 时，带状的植被斑图清晰可见，并垂直于x方向(图2(g))。从整个过程可以看出，不同方格上的植被生物量的振幅逐渐变大。当 $a_v=20$ 时，带状植被斑图按照类似的过程逐渐形成。

对比不同 $a_v$ 形成带状植被斑图的过程，可以看出，在同样的时间长度下，较大的 $a_v$ 使得植被生物量远离平衡点产生的振幅更大，这导致在 $t=100$ 时，图2(g)的带状斑图的振幅很小，而图2(h)中的带状斑图振幅却很大，植被生物量的最小值甚至减少到0。在 $a_v=0$ 时，想要得到类似于图2(h)的振幅，需要大约 $t=500$。同时，对比两图也可以清晰地看到，较大的 $a_v$ 形成了较窄的植被带。

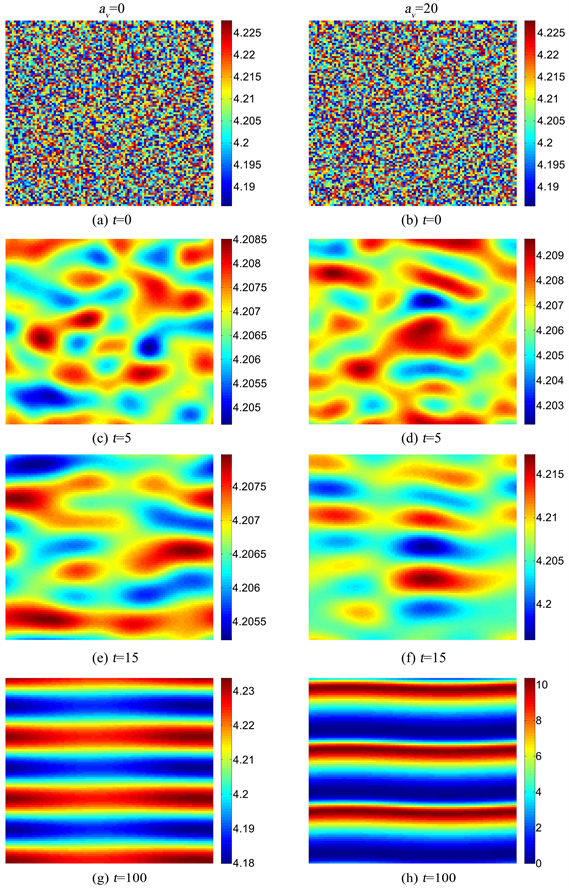
Figure 2. Vegetation pattern formation with different a_v

图2. 不同a_v下的植被斑图形成

图3展示了在 $\left(x,50\right)$ 坐标方格上( $y=50$ 的直线)的v和w的生物量的变化曲线。其中绿线代表v的值，而蓝线代表w的值。在图3(a)中，虚线代表 $t=480$ 的值，实线代表 $t=500$ 的值。在图3(a)中，虚线代表 $t=80$ 的值，实线代表 $t=100$ 的值。容易得出，图3(a)和图3(b)中虚线和实线均有时间差 $\Delta t=20$。因此，带状植被带并不是静止的，而是沿着x方向移动，即坡的方向。同时可看出 $a_v=20$ 时，植被带的移动速度有所降低。

Figure 3. Variations of v and w on lattice $\left(x,50\right)$ (line $y=50$ )

图3. 在 $\left(x,50\right)$ 坐标方格上( $y=50$ 的直线）的v和w的变化曲线

6. 结论

考虑坡面水流对植被种子传播的影响，将交叉对流项引入Klausmeier模型；基于改进的模型，进行了图灵分岔分析和斑图形成的数值模拟。结果显示，交叉对流的存在，使得系统更容易发生图灵分岔。斑图形成的模拟结果显示，交叉对流的存在使得系统发生分岔远离平衡点的速度加快(相同时间长度后斑图中的振幅更大)，产生的植被带更窄。从植被与水的切面图可以看出，斑图稳定后，交叉对流项使得植被带的移动速度减慢。