1. 引言
随着科技的发展,移动机器人在农业机械,智能交通还有智慧城市等领域都有不凡的表现,而机器人的路径规划是学术界研究的一个热点及难点问题。路径规划简单来说,就是设定起点与终点两个点,通过智能算法在可行路径上规避障碍物,获得一个安全无碰撞,距离最短的路径。常用的评价指标有规划路径的长短信息,用时大小以及拐角频率等 [1] [2] [3]。另外,还可以从面对的场景,环境信息的不同,分为全局路径规划和局部路径规划 [4]。全局路径规划主要使用的是静态地图,在先验信息已知的情况下规划路径,常见的算法有传统算法包括Dijkstra算法 [5]、A*算法 [6] [7] 等,智能算法包含粒子群优化算法,蚁群算法,遗传算法等。而局部路径规划面对对象通常为动态环境,在环境完全未知或者部分已知的前提下,基于多传感器识别局部环境,形成实时路径规划,常用的算法有动态窗口法(DWA),人工势场法(APF),模糊逻辑法(FL)等。
文献 [8] 使用A*算法解决了AGV无冲突路径规划问题。文献 [9] 将A*算法应用到了农业场景中,提高了采摘机器人的工作效率和控制精准度。张超等人 [10] 运用Dijkstra算法思想,在输电线路选线方面发挥了作用。以上文献均涵盖了全局路径规划思想,涉及不同的领域,因此,对两种经典全局路径规划算法展开研究显得尤为重要。
2. 全局路径规划
全局路径规划是导航功能中重要的一环,导航包中常常出现,导航包调用全局路径规划器,并且是以插件的形式,插件接收全局地图,以及人为设定的起点和目标点等信息,经过算法处理,输出处理好的全局路径信息。
2.1. Dijkstra算法
本文将通过复现Dijkstra算法的实现过程,详细地一步一步说明,来体会理解算法的核心思想,即Dijkstra算法将所有点的最短代价按照由近及远的顺序一一计算。在说明算法之前,需要进行情景假设,首先确定起始点,行走过程中,一次只能前进一格,不能够越过格子,所以可以得到周围八个相邻的格子。如果走上下左右四个方向的话,计它路程为2。如果走左上、左下、右上、右下,那么就计它路程为3。这里定义两个数组,一个是用来存放待确定路径的点,取名为openlist = [ ],另一个是用来存放已确定路径的点,取名为closedlist = [ ]。说明一下,在Python里面是列表,如果在其他语言也可以设置为数组。根据命名规则,每个点通过下标信息都能记录其父节点,在提取路径时一目了然。不走已确定路径的点,即已放进closedlist的点。为了方便讲解,约定起点为S点,相邻的8个点以A~H来称呼表示它的方向。第一步我们以S点为起点,把它放进closedlist里面,然后再计算S点的相邻8个点,那么由S点这个中心点出发,上下左右,这么直走,计它路程为2,斜走为3,然后结合刚刚的命名规则,左面这个点2,它是在S点的B方向,所以是BS = 2,所以BS这个点就代表了这个2。然后下面也是同理,DS是D方向,斜走也是一样,A方向是3,斜走是3,所以AS = 3,这么计算下来就把8个点都算出来,放进openlist里面。如图1(a)所示。
第二步要进行中心点的选取,在openlist里面取一个最小值的点作为选取点,可以看到openlist里面一共有四个2,这里先按上下左右的顺序去依次计算。首先取上面这个2,它是HS点,那么第二步计算就以HS点为中心点来进行,在这个图上可以看到,在HS点这个位置点了个小红点让它更醒目一些,然后在周围加一个小框框把它框柱,代表它周围8个相邻的点要进行计算,那么就把HS点从openlist里面取出放进closedlist里面,然后再计算它相邻的8个点去累计路程。可以看到它周围的8个点有好几种情况,首先它下方这个点是S点,S点作为起点已经被放进closedlist里面,那么这个点是不需要计算的。然后第二种情况是,它旁边的两个3和下方的两个2在上一步已经被计算过了,在这一步的时候就是存在这么一种情况,就是点已经在openlist里面,针对这种情况就要判断一下,选取路程较小的方案。举一个例子,我们先来看一下这个3,这个3是怎么来的呢,是一开始从S点斜走一步取3,在第二步从HS点出发往左走一步也能到达这个点,但是这种方案的话就是2 + 2 = 4,因为它走了两步,先从S点往上走一步,再往左走一步,那就是2 + 2 = 4,4 > 3,那么就取第一种方案3。那么右边这个3和下面的两个2都是同样的道理,它们原来的值更小那么就保留它们的值。那么第三种情况是HS点的上方三个点本来是空白的,它没有在openlist里面,那么这里就要计算它的值,例如这个4就是BS点往上走一步,就是2 + 2 = 4,我们把这个4的点取名为HHS,这个命名规则是这样的,这个下标代表它的父节点HS,然后它本身的H就是代表它的方向,它在中心点的上方就是取H,那么这个点就是HHS = 4。那么下面的AHS = 5也是一样的道理,在这个地方HS这个中心点斜上走一步就是5,这个AHS,然后再把这三个计算好的点放进openlist里面,那么到这里就可以认为,在closedlist里面的HS这个点,它是最小路径,因为它每走一步都是正数,没有中转点使得S到HS的路程缩短。这个结论在后面的每一步都是成立的,这样就能保证我们通过Dijkstra这种算法,算出来的最后的路径是一个最优解。如图1(b)所示。
再来看一下第三步,继续在openlist里面去取一个最小的点,以DS作为中心点进行第三步,首先把它从openlist里面提取出来,放到closedlist里面,然后再重复第二个步骤,计算它相邻的8个点,然后进行累计路程,对于点已存在openlist,取路程小的方案。DDS = 4表示从S点出发,第一个D就代表D方向走一步,然后第二个D就是再往下走一步,那么就得到了2 + 2 = 4。CDS = 5是从S点出发往D方向走一步,再往C方向走一步,是2 + 3 = 5,最后一个点EDS也是类似。如图1(c)所示。
第四步,继续在openlist里面取一个最小的点作为第四步的中心点,这里就取左边这个2,把这个BS放进closedlist里面,继续重复上面的步骤计算它相邻的8个点,累计路程,然后得到三个新增加的点,把它们也放到openlist里面。如图1(d)所示。
第五步也是一样的做法,取右边这个FS=2为中心点,把中心点FS放到closedlist里面,经过计算也增加了三个新的点。那么到这一步,就已经把2的值算完了,下面开始算3的值,因为3是最小的。如图1(e)所示。
第六步,取AS = 3这个点作为中心点,重复跟前面一样的步骤,可以看到它相邻的8个点有3个点,这三个点已经标了红点,它们已经被放进closedlist里面,那么这三个点就不用计算,还有两个4和两个5已经存在openlist里面了,我们就可以对比它的路程,取路程小的一个方案。看一下这个5,这个5原本是怎么来的呢,是从S点出发往左走一步等于2,然后再往斜上走一步是5,2 + 3 = 5。如果以AS为中心,往左走一步,3 + 2也是等于5,那么在这种相等的情况下我们就可以把原来的方案替换也可以不替换,其实这等于是两种相同路程的路径,一种是先往左走一步,再往斜上走一步,另一种是先往斜上走一步,再往左走一步,它们的距离都是5,那么这里就不进行替换,取原来的那种方式,最后就只新加了一个6,斜走两步,3 + 3 = 6,那么下面的步骤也是一样的。如图1(f)所示。
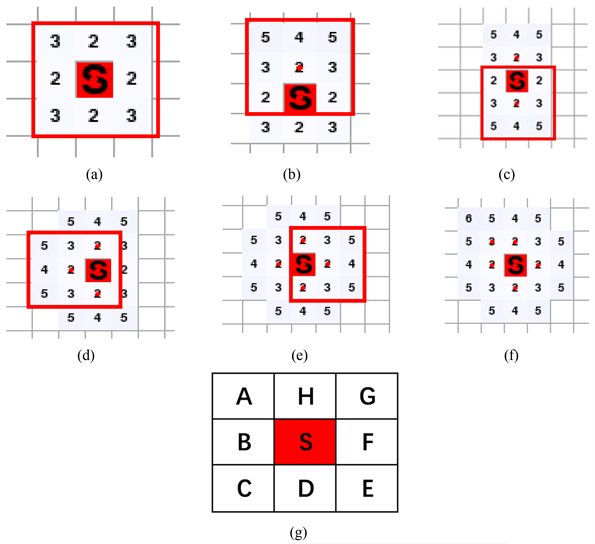
Figure 1. Dijkstra algorithm demonstration
图1. Dijkstra算法演示
2.2. A*算法
介绍A*算法之前,先说明一下两种距离。第一个是欧几里得距离,也是经常用的一个概念,在二维的空间中,要算两个点之间的距离,可以直接用直线两两相连,计算公式如式(1)所示:
(1)
第二种距离是曼哈顿距离,这个名字的由来不是提出这个概念的人叫曼哈顿,而是他提出了一个在纽约曼哈顿的情景,建筑物就是障碍物,我们需要打车到目的地,不可能使用欧几里得距离,直接穿过障碍物,出租车只能沿着马路走,所以曼哈顿距离又称出租车距离,计算公式如式二所示:
(2)
对比两种距离,欧几里得距离计算量将大大增加,但方向性很强,而曼哈顿距离计算量相对较小,但会存在很多距离等效的路线。
接下来,看一下A*算法的关键,估算函数,它的公式如下所示:
(3)
式中,G代表从起点到当前节点实际路程,H代表从当前节点到终点最小估算路程,使用曼哈顿距离、或欧几里得距离,F代表从起点到终点估算路程,下面将围绕这个核心公式,讲解A*算法的实现过程。
情景假设与Dijkstra算法类似,不同的是算H估算距离时,忽略障碍物。首先第一步,以S点为中心点,根据估算函数来计算它周围的八个点,它们的父节点为S,首先来看G,G的含义是起点到当前节点实际路程,周围的八个点,直走为2,斜走为3,跟Dijkstra算法相同,不同之处是还得加上一个估算路程。以FS点为例,从起点左走为2,即G值为2,H值采用曼哈顿距离,根据公式,通过数格子的方式计算估算距离,X方向上,差三格,Y方向上,差五格,一个格子计为2,F值即为3*2 + 5*2,加上G的值2,得到F值为18。如图2(a)所示。
G、H和F值构成openlist和closedlist里的内容,其中最小的F值决定下一步的中心点选择,由此判断,ES为下一步的中心点。第二步,将ES点从openlist里面取出,放进closedlist,加个红点,表示已放入,加上红框,计算它周围的八个点。第一种情况为S点,已经在closedlist里面,不必计算。第二种情况,点在openlist里面,比较G值,取G值较小的结果。如图2(b)所示。
第三步取EES点作为中心点,重复步骤,遇到障碍物或者已经存在closedlist的情况,直接略过,其余的点就按照F = G + H来计算。如图2(c)所示。
重复以上步骤,得到F值最小的点即DEFEES,通过父节点反推,从而获取路径信息。
3. 对比仿真实验
本文采用栅格地图进行仿真,左上角为零点。在同一张地图上,设置相同的起点与终点,来对比两种算法的异同之处。
图3(a)~(b)两图为简单地图上分别运行A*算法和Dijkstra算法,图3(c)~(d)两图为较复杂地图上分别运行Dijkstra算法和A*算法。从对比仿真的结果入手,可以发现两种算法的异同点。如图所示,红色S点表示起点,终点用黄色G点表示,基于前文的介绍,从起点到终点的路径长短信息可以用数字的大小来表示,且为了方便呈现出来,通过加深蓝色来代表距离的增长,即距离越长颜色越深。观察两图可以发现,简单的图中,两种算法虽然路径方案不同,但路程长短相同,用数字表示均为44。图3(a)从起始点向E方向前进一格,计为3,接着朝F方向前进,依次增加2,直到来到代价为23的点,再次向E方向前进一格,加3变为26,最后向着D方向前进,一格计为2,来到终点44。图3(b)是先朝着F方向前进,以2为步长,路程代价增加为20,再向E方向前进2格,步长为3,来到之前的代价为26处,之后的步骤与图3(a)相同。接着,将障碍物增多,地图复杂化,选取起点和终点,总代价均为49,对比两图的区别,在代价数字为11处出现不同的行进路线,图3(c)向F方向拓展,而图3(d)向E方向前进,两图分别在25和32处进行新的转折。
分析一下两种算法出现两种路径方案的现象,可以得到两个算法实现的差异之处。Dijkstra算法是遍历中心点周围所有的点,选取代价最小的,而A*算法是引入估算函数,具有方向性,结果就导致了选取方案的差别。A*算法由于存在方向性函数的指引,计算量大大减小,而Dijkstra算法搜索区域较大,花费时间较长。简单对比一下两者:Dijkstra是一种基于广度优先的算法,操作过程如下,从起点开始由近到远去遍历所有的点,把起点到每一个点的路径都算出来,然后由近及远都算一遍,直到遇到了目标点,那么就把起点到目标点这个路径给提取出来,这个就是广度优先,特点是把每个点都算了一遍。而A*算法是一种基于深度优先思想的算法,并没有从起点开始把每个点都算一遍,而是目标点对路径规划有一个方向性的指引作用,它会优先朝着目标点方向去计算,计算量将远远小于前者。另外一个特点是Dijkstra算法能保证路径一定是最短最优的路径,而A*算法找的路径不一定是最优解。
4. 结语
通过对比Dijkstra算法与A*算法的实现过程,加深了对全局路径规划的理解。本文用数字将路径代价量化,清晰地表示了距离信息,字母表示中心点周围的方向,按照算法原理选取中心点位置,直至遍历到目标点,读取父节点信息,得到路径方案。仿真结果表明,算法实现过程有效,能够展现两种算法的异同点。