1. 引言
四旋翼无人机具有重量轻、尺寸小、机动性高、隐蔽性好、结构简单、造价低、适应性强等一系列特点。目前,其已广泛应用于航拍、侦察监视、通信中继、目标搜索与跟踪、大地测量、城市环境检测 [1] 等军事及民用领域中。
另一方面,现代精密系统对其各部件可靠性的要求越来越高,系统内部各个环节的故障都可能导致整个系统性能下降,甚至失控 [2] [3]。通常,根据故障发生部位的不同可将其分为执行器故障、传感器故障及结构故障。而执行器故障在实际的工程应用中又最为常见。对于四旋翼无人机而言,桨叶是最重要的执行机构之一,其由电机带动旋转,与周围空气相互作用,产生沿旋翼轴的推力 [4]。值得一提的是,桨叶在高速旋转的过程中,常常发生振动,这会导致桨叶的磨损加快、使用寿命减少,并且严重的振动还会导致桨叶的断裂或破损。此外,四旋翼无人机在执行任务的过程中,存在撞击到障碍物的可能,这往往也会导致桨叶尖端出现破损或断裂。这些不利因素都会直接影响到四旋翼无人机所能产生的推力的大小,从而影响四旋翼无人机的性能。因此,有必要从机理上分析及计算桨叶缺损后所能产生的实际推力。
目前,四旋翼无人机的动力学分析方法主要包含桨叶动量定理、叶素理论、计算流体动力学(Computational Fluid Dynamics, CFD)方法等 [5] [6]。其中桨叶动量定理一般把旋翼视为一个无限薄的圆盘,利用气流流动的基本定律来研究旋翼圆盘对气流的作用 [7]。其主要特点及优势是计算原理简单,常用于旋翼性能的初步估算、桨叶总体参数选择等分析计算中。然而,桨叶动量理论也存在局限性,其不涉及对桨叶几何特性的分析,故仅利用动量定理还不足以分析桨叶缺损的情况。因此,研究者们提出了叶素理论 [8] [9],其思想为将桨叶看作无限多个叶素,并假设每个叶素为一个二维翼型。因此可应用二维翼型特性来计算桨叶剖面的气动力,然后沿桨叶径向积分可得单片桨叶及整个螺旋桨的气动力。此外,近些年,CFD逐渐被广泛地用于直升机空气动力学研究,其优势是能分析旋翼在复杂运动情况下的非定常空气动力特性 [10],相较于前两种方法而言,有更高的准确性,但相应地其计算原理也更为复杂。关于建立四旋翼无人机桨尖缺损故障数学模型这一问题,可借助上述三种方法进行分析计算。然而,由于四旋翼无人机相较于直升机而言,其结构及气动特性都更为简单,为简化建模过程,前两种方法更为常用。
受上述研究成果的启发,为快速、简便地获得四旋翼无人机桨尖缺损故障模型,从而为后续设计四旋翼无人机飞行控制策略提供基础,本文综合桨叶动量定理与叶素理论,先利用前者计算桨叶上的来流速度,然后利用后者分析四旋翼无人机桨尖缺损后桨叶剖面所能产生的实际推力,并对缺损桨叶沿径向积分,从而计算出缺损后单片桨叶及整个螺旋桨的气动力。
本文的主要结构为:第2介绍桨叶动量定理与叶素理论的基础知识,第3节具体阐述桨尖缺损故障的建模过程,第4节给出算例,最后第5节总结本文的结论。
2. 基本知识
桨叶的空气动力学描述了桨叶在空气中旋转的运动规律,揭示了四旋翼无人机桨叶产生推力的机理,其计算主要基于动量定理及叶素理论。本小节将重点介绍这两种理论的基础知识。
2.1. 桨叶动量定理
在桨叶动量定理中,螺旋桨通过一个被视为能对气流产生作用力的圆盘,并受到气流对其的反作用力。存在如下假设 [4] [6]:
1) 穿过圆盘的空气流管与外部气流不存在相互作用;
2) 螺旋桨包含了无限多个桨叶元素;
3) 圆盘厚度无限薄;
4) 通过圆盘的气流的垂直速度是连续的;
5) 空气不可压缩。
那么针对单片桨叶,它所能提供的推力
(即通过圆盘的空气动量的变化)与桨盘上下方的压力差成正比,具体为:
(1)
其中A为桨盘面积,
为通过圆盘的空气质量的变化,
为空气密度,
及
分别为桨盘正上方及正下方的压强,而
为桨盘正上方的空速,
及
分别为桨盘上方及下方无限远处的空速。图1给出了动量定理模型的示意图。

Figure 1. The diagram of blade model in momentum theory
图1. 桨叶动量定理模型示意图
2.2. 叶素理论
动量定理虽然能计算出桨叶所能提供的推力,但其对细节的分析还不够充分,仅仅利用动量定理还不足以能对桨尖缺损故障进行建模。因此,计算螺旋桨的总气动力和气动力矩往往需借助叶素理论并结合动量定理,具体为:对作用在桨叶元素上的气动力进行积分来计算出整个螺旋桨的总气动力。
如图2所示,对于单片桨叶的一个无限小横截面,根据空气动力学理论,可计算其升力
与阻力
(2)
其中
为来流速度
在水平方向上的分量(如图2所示),
分别为升力系数及阻力系数,c为桨叶的平均弦长,r为所选取的桨叶剖面的径向位置。
升力系数
以大小为a的升力斜率随迎角
线性变化,其具体表达式为:
其中
为叶片弦线与水平线之间形成的入射角,
为局部入流角。此外,假设叶片扭向随叶剖面的径向位置线性变化,那么
可以表示为:
其中
为桨叶的零入射角,
为扭转入射角,R为桨叶半径。

Figure 2. The diagram of force analysis on the blade section
图2. 桨叶剖面受力分析示意图
利用小角度近似原理,可将
的形式定义为:
其中
分别为来流速度
在垂直方向上的分量。
至此,无限小横截面的升力
可写成如下形式:
(3)
同样根据小角度近似原理,无限小横截面的垂直方向上的推力
可被简化为:
(4)
对
在
区间求积分即可得到单片桨叶所能产生的推力
,具体为:
(5)
3. 桨尖缺损故障建模
本小节将分析当四旋翼无人机桨尖缺损后所能产生的推力大小,并以此建立桨尖缺损故障模型。
首先根据式(5),需要分别计算
及
,容易得到
的表达式为:
其中
为桨叶转速,r为所选取的无限小横截面的径向位置。
而计算
需要结合动量定理。首先对于每一个叶片元素来说,
的值均相同。根据伯努利(Bernoulli)方程可知:
其中
为桨盘正下方的空速。
又由于
且
,故有
那么,可以进一步得到桨盘上的来流速度
为:
为了简化问题,考虑无人机处于悬停状态,有
且
,故
。
结合式(1),至此,整片桨叶产生的推力T可写为:
其中有
。
在悬停状态下,有
其中m为无人机的质量,g为重力加速度。故可以得到:
将来流速度
与桨尖速度作比,得到来流比
,其具体形式如下:
可以看出对于一个给定的四旋翼飞行器,来流比是一个定值。反过来,
可以写为:
(6)
现假设单片桨叶在桨尖处出现缺损,然后将缺损后的桨叶半径与初始桨叶半径R之间的比例定义为桨尖缺损比k,有
,其能直接反映桨尖缺损程度。结合式(5),下述表达式给出了桨尖缺损后该桨叶所产生的推力:
随后,得到一个桨尖对称缺损的螺旋桨所产生的推力:
其中将
定义为发生桨尖缺损故障后螺旋桨产生的推力与原有推力之比,有
可以看出
并非随桨尖缺损比线性变化,两者之间呈一种较为复杂的非线性关系。为了简化问题,我们不直接研究桨尖缺损比与推力的关系,而是把
作为一个未知整体,从而将桨尖缺损故障建模为控制能效损失故障。该种故障的数学形式可以表示为:
其中
为正常情况下一个螺旋桨所产生的升力,而
通常满足
。可以看出,当桨尖缺损程度越严重时,
越小,反之亦然。
4. 算例
本小节以文献 [6] 的四旋翼无人机桨叶参数为例,参数具体设定为:
绘制实际推力与原有推力之比
随桨尖缺损比k变化的曲线,如图3所示。从图中可以看出,当四旋翼无人机出现桨尖缺损,
随桨尖缺损程度呈非线性变化,且当缺损程度较低时,
会随缺损程度的增大出现较大幅度的减小,即实际推力大幅减小,例如当桨尖从未缺损变化到缺损30%时,
从1减小至约0.4,而当缺损程度较高时,随着缺损程度的进一步增大,
的减小幅度将有所放缓,即实际推力减小速度放缓,例如当桨尖从缺损70%变化到缺损约100%时,
从约0.05减小至约0。
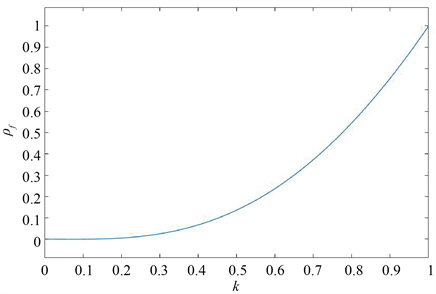
Figure 3. The curve of
with respect to k
图3.
随k变化曲线
5. 结论
本文综合利用桨叶动量定理与叶素理论,从机理上定量计算了四旋翼无人机出现桨尖缺损这一执行机构故障后桨叶所能产生的实际推力,从而建立了桨尖缺损故障的数学模型。这将为后续的飞行控制算法设计提供基础。作者在未来的研究工作中,也将基于本文所获得的故障模型,探索四旋翼无人机在桨叶缺损故障下的飞行控制问题。
基金项目
中央高校基本科研业务费(B200201047)。
NOTES
*通讯作者。