六次广义Ball曲线的两种推广

Two Extensions of Sextic Generalized Ball Curves

摘要: 构造了两组含形状参数的多项式基函数，并以此构造了两组带形状参数的全新Ball曲线。一组囊括了六次Wang-Ball曲线与Said-Ball曲线以及二者之间的大量曲线；另一组则包含了六次Said-Ball曲线与Bézier曲线以及介于二者之间的大量曲线。通过对两组曲线与六次Bézier曲线关系的分析，得出了形状参数的几何意义，并通过Bézier方法中的递归分割算法求得到了两组新曲线的几何作图法。

Abstract: Two classes of polynomial basis functions with shape parameter are constructed. Based on these two bases, two new Ball curves with shape parameter are defined. The former curve contained the sextic Wang-Ball and Said-Ball curve and a large number of curves between these two curves. The latter includes the sextic Said-Ball and Bézier curve and a large number of curves between these two curves. Through the analysis of the relationship between the two kinds of curves and the gen-eral sextic Bézier curve, the geometric meaning of the shape parameters is obtained, and the geo-metric drawing method of the two kinds of new curves are given out in virtue of the de Casteljau al-gorithm of the general Bézier curve.

1. 引言

自三次参数曲线 [1] 被提出以来，许多学者针对广义Ball曲线曲面进行深入研究，并得到了相当的成果。文献 [2] 中，Hu、Wang等人提出了Wang-Ball和Said-Bezier曲线。文献 [3] 中，邬弘毅教授又在Wang-Ball、Said-Ball曲线与Bezier、Said-Ball曲线的基础上提出了两种全新的广义曲线。文献 [4] 中，Pelgado和Pena定义了DP-Ball基。经过大量实践发现，Ball曲线具有与一般Bezier曲线类似的保形性质，但该曲线在求值方面更加快捷，升阶和降阶的计算难度更加简单。因此，在工业设计中，Ball曲线愈发被重视。

文献 [5] 中，作者利用增加基函数次数的方式，重新构造了一种带有形状参数的基函数，由之所定义的曲线拥有类似三次Ball曲线的性质。文献 [6] 与 [7] 分别通过引入位置参数构造出两种不同的广义Ball曲线。文献 [8] 针对四次Ball曲线进行扩展。文献 [9] 和 [10] 均针对五次Ball曲线进行了扩展。为了进一步丰富广义Ball曲线的理论，这里以六次Ball曲线为研究对象，通过引入新的形状参数，重新构造了两组不同的基函数，进而实现六次Wang-Ball基与Said-Ball基向Said-Ball基与Bernstein基的转变。此外，由两组新基所构造的曲线具备形状调整能力，当前一组基函数中的形状参数改变时，相关曲线可转变包括六次Wang-Ball曲线与Said-Ball曲线在内的多种曲线；当后一组基函数中的形状参数改变时，与之相关的曲线可以转变为包括六次Said-Ball曲线与Bernstein曲线在内的多种曲线。

2. 介于Wang-Ball和Said-Ball曲线之间的曲线

2.1. 基函数及其性质

定义1 对于任意 $t\in \left[0,1\right]$，称多项式

$\{\begin{array}{l}{b}_{0,6}\left(t\right)=\left(1-2\alpha t+\alpha t^2\right){\left(1-t\right)}^2\\ b_{1,6}\left(t\right)=\left(2+2\alpha -4\alpha t\right)t{\left(1-t\right)}^3\\ b_{2,6}\left(t\right)=\left(4+6\alpha \right)t^2{\left(1-t\right)}^4\\ b_{3,6}\left(t\right)=\left(8+12\alpha \right)t^3{\left(1-t\right)}^3\\ b_{4,6}\left(t\right)=\left(4+6\alpha \right)t^4{\left(1-t\right)}^2\\ b_{5,6}\left(t\right)=\left(2-2\alpha +4\alpha t\right)t^3\left(1-t\right)\\ b_{6,6}\left(t\right)=\left(1-\alpha +\alpha t^2\right)t^2\end{array}$， $t\in \left[0,1\right]$ (1)

为带一个形状参数 $\alpha$ 的六次广义Ball基函数，为了便于下文称呼，在此简称其为 $\alpha \text{-}B$ 基，其中 $0\le \alpha \le 1$。

$\alpha \text{-}B$ 基特性如下：

特性1 非负性和规范性。即 $b_{i,6}\left(t\right)\ge 0\left(i=0,1,\cdots ,6\right)$ 且 ${\displaystyle \underset{i=0}{\overset{6}{\sum }}{b}_{i,6}\left(t\right)}=1$。

特性2 对称性。即 $b_{i,6}\left(t\right)=b_{6-i,6}\left(1-t\right),i=0,1,\cdots ,6$。

特性3 端点性质。

$\{\begin{array}{l}{b}_{0,6}\left(0\right)=1\\ b_{i,6}\left(0\right)=0,i=1,2,\cdots ,6\end{array};\{\begin{array}{l}{b}_{i,6}\left(1\right)=0,i=0,1,\cdots ,5\\ b_{6,6}\left(1\right)=1\end{array}$， $\{\begin{array}{l}{b^{\prime }}_{0,6}\left(0\right)=-\left(2\alpha +2\right)\\ {b^{\prime }}_{1,6}\left(0\right)=2\alpha +2\\ {b^{\prime }}_{i,6}\left(0\right)=0,i=2,3,4,5,6\end{array};\{\begin{array}{l}{b^{\prime }}_{i,6}\left(1\right)=0,i=0,1,2,3,4\\ {b^{\prime }}_{5,6}\left(1\right)=-\left(2\alpha +2\right)\\ {b^{\prime }}_{6,6}\left(1\right)=2\alpha +2\end{array}$

特性4 单峰性。在区间 $\left[0,1\right]$ 上，任意基函数有唯一最大值，相关验证可通过对基函数求导证明。

特性5 退化性。当 $\alpha =0$ 时， $\alpha$ B基为六次Wang-Ball基；当 $\alpha =1$ 时， $\alpha \text{-}B$ 基转化成六次Said-Ball基。

2.2. 曲线的构造及特性

定义2 给定特征点 $P_i\in R^d\left(d=2,3;i=0,1,\cdots ,6\right)$，称曲线

$p\left(t\right)={\displaystyle \underset{i=0}{\overset{6}{\sum }}{P}_i}{b}_{i,6}\left(t\right)$， $t\in \left[0,1\right]$ (2)

为带形状参数 $\alpha$ 的六次广义Ball曲线，简称 $\alpha \text{-}B$ 曲线。

由 $\alpha$ B基的性质可推得 $\alpha$ B曲线具如下特性：

特性1 端点性质

$p\left(0\right)=P_0$， $p\left(1\right)=P_6$ ； $p^{\prime }\left(0\right)=\left(2\alpha +2\right)\left(P_1-P_0\right)$， $p^{\prime }\left(1\right)=\left(2\alpha +2\right)\left(P_6-P_5\right)$。

该性质这说明 $\alpha \text{-}B$ 曲线经过控制多边形的首末边相切，切点分别为首端点 $P_0$ 与末端点 $P_6$。

特性2 凸包性。由 $\alpha \text{-}B$ 基的非负性和规范性可得，曲线整体位于由控制多边形构成的凸包内部。

特性3 对称性。由控制多边形 $P_0{P}_1\cdots P_6$ 和 $P_6{P}_5\cdots P_0$ 构成的两条 $\alpha$ B曲线形状相同，但方向相反。

特性4 几何不变性与仿射不变性。规范基表示的曲线不会因坐标系的选取而有所改变，因而 $\alpha \text{-}B$ 曲线拥有几何不变性。此外，对 $\alpha \text{-}B$ 曲线的控制多边形进行仿射变换之后，若想得到与后者相关的曲线，只需对前者的相应曲线进行相同变换即可，因此该曲线具备仿射不变性。

2.3. 形状参数的几何意义

为分析参数 $\alpha$ 变化时对曲线形状所造成的影响，将针对 $\alpha \text{-}B$ 曲线中的参数 $\alpha$ 的几何意义进行讨论。

将 $\alpha \text{-}B$ 基改写为

$\{\begin{array}{l}{b}_{0,6}\left(t\right)=B_{0,6}\left(t\right)+\frac{4-2\alpha }{6}{B}_{1,6}\left(t\right)+\frac{6-5\alpha }{15}{B}_{2,6}\left(t\right)+\frac{4-4\alpha }{20}{B}_{3,6}\left(t\right)+\frac{1-\alpha }{15}{B}_{4,6}\left(t\right)\\ b_{1,6}\left(t\right)=\frac{2+2\alpha }{6}{B}_{1,6}\left(t\right)+\frac{4}{15}{B}_{2,6}\left(t\right)+\frac{2-2\alpha }{20}{B}_{3,6}\left(t\right)\\ b_{2,6}\left(t\right)=\frac{4+6\alpha }{15}{B}_{2,6}\left(t\right)\\ b_{3,6}\left(t\right)=\frac{8+12\alpha }{20}{B}_{3,6}\left(t\right)\\ b_{4,6}\left(t\right)=\frac{4+6\alpha }{15}{B}_{4,6}\left(t\right)\\ b_{5,6}\left(t\right)=\frac{2-2\alpha }{20}{B}_{3,6}\left(t\right)+\frac{4}{15}{B}_{4,6}\left(t\right)+\frac{2+2\alpha }{6}{B}_{5,6}\left(t\right)\\ b_{6,6}\left(t\right)=\frac{1-\alpha }{15}{B}_{2,6}\left(t\right)+\frac{4-4\alpha }{20}{B}_{3,6}\left(t\right)+\frac{6-5\alpha }{15}{B}_{4,6}\left(t\right)+\frac{4-2\alpha }{6}{B}_{5,6}\left(t\right)+B_{6,6}\left(t\right)\end{array}$ (3)

(3)式可用矩阵表示为

$b=MB$

其中

$b={\left(\begin{array}{cccc}{b}_{0,6}\left(t\right)& b_{1,6}\left(t\right)& \cdots & b_{6,6}\left(t\right)\end{array}\right)}^{\text{T}}$

$M=\left(\begin{array}{ccccccc}1& \frac{4-2\alpha }{6}& \frac{6-5\alpha }{15}& \frac{4-4\alpha }{20}& \frac{1-\alpha }{15}& 0& 0\\ 0& \frac{2+2\alpha }{6}& \frac{4}{15}& \frac{2-2\alpha }{20}& 0& 0& 0\\ 0& 0& \frac{4+6\alpha }{15}& 0& 0& 0& 0\\ 0& 0& 0& \frac{8+12\alpha }{20}& 0& 0& 0\\ 0& 0& 0& 0& \frac{4+6\alpha }{15}& 0& 0\\ 0& 0& 0& \frac{2-2\alpha }{20}& \frac{4}{15}& \frac{2+2\alpha }{6}& 0\\ 0& 0& \frac{1-\alpha }{15}& \frac{4-4\alpha }{20}& \frac{6-5\alpha }{15}& \frac{4-2\alpha }{6}& 1\end{array}\right)$

$B={\left(\begin{array}{cccc}{B}_{0,6}\left(t\right)& B_{1,6}\left(t\right)& \cdots & B_{6,6}\left(t\right)\end{array}\right)}^{\text{T}}$

若记

$P=\left(\begin{array}{cccc}{P}_0& P_1& \cdots & P_6\end{array}\right)$

则 $\alpha \text{-}B$ 曲线可表示为

$p\left(t\right)=PMB$ (4)

记

$V=\left(\begin{array}{cccc}{V}_0& V_1& \cdots & V_6\end{array}\right)$

若令

$p\left(t\right)=VB$ (5)

即利用传统的六次Bézier曲线表示 $\alpha \text{-}B$ 曲线。其中， $V_i\left(i=0,1,\cdots ,6\right)$ 为普通Bézier曲线的特征点。则由式(4)和(5)可得Bézier曲线与 $\alpha \text{-}B$ 曲线的控制顶点之间的关系式

$V=PM$ (6)

即

$\{\begin{array}{ll}{V}_0=P_0\hfill & (\text{a})\hfill \\ V_1=\frac{4-2\alpha }{6}{P}_0+\frac{2+2\alpha }{6}{P}_1\hfill & (\text{b})\hfill \\ V_2=\frac{6-5\alpha }{15}{P}_0+\frac{4}{15}{P}_1+\frac{4+6\alpha }{15}{P}_2+\frac{1-\alpha }{15}{P}_6\hfill & (\text{c})\hfill \\ V_3=\frac{4-4\alpha }{20}{P}_0+\frac{2-2\alpha }{20}{P}_1+\frac{8+12\alpha }{20}{P}_3+\frac{2-2\alpha }{20}{P}_5+\frac{4-4\alpha }{20}{P}_6\hfill & (\text{d})\hfill \\ V_4=\frac{1-\alpha }{15}{P}_0+\frac{4+6\alpha }{15}{P}_4+\frac{4}{15}{P}_5+\frac{6-5\alpha }{15}{P}_6\hfill & (\text{e})\hfill \\ V_5=\frac{2+2\alpha }{6}{P}_5+\frac{4-2\alpha }{6}{P}_6\hfill & (\text{f})\hfill \\ V_6=P_6\hfill & (\text{g})\hfill \end{array}$ (7)

若记 $Q_1=\frac{P_0+P_6}{2},Q_2=\frac{P_1+P_5}{2}$，则式(7)中的(d)式可变换为

$\begin{array}{c}{V}_3=\frac{2-2\alpha }{5}\frac{P_0+P_6}{2}+\frac{1-\alpha }{5}\frac{P_1+P_5}{2}+\frac{2+3\alpha }{5}{P}_3\\ =\frac{2-2\alpha }{5}{Q}_1+\frac{1-\alpha }{5}{Q}_2+\frac{2+3\alpha }{5}{P}_3\\ =P_3+\frac{2-2\alpha }{5}\left(Q_1-P_3\right)+\frac{1-\alpha }{5}\left(Q_2-P_3\right)\end{array}$ (8)

由式(7)中(b)式可知， $V_1$ 分边 $P_0{P}_1$ 的比为 $1+\alpha :2-\alpha$ ；由式(7)中(f)式可知， $V_5$ 分边 $P_5{P}_6$ 的比为 $2-\alpha :1+\alpha$ ；由公式(8)可知， $V_3$ 处于以 $\frac{2-2\alpha }{5}\left(Q_1-P_3\right)$ 和 $\frac{1-\alpha }{5}\left(Q_2-P_3\right)$ 为邻边的平行四边形的终点处。参数 $\alpha$ 的几何意义如图1所示， $\alpha$ 取值为0， $P_0{P}_1\cdots P_6$ 为 $\alpha$ B曲线的特征多边形， $V_0{V}_1\cdots V_6$ 为表示 $\alpha \text{-}B$ 曲线的Bézier曲线的特征多边形。

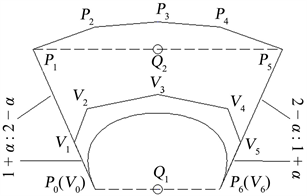
Figure 1. The geometric meaning of shape parameter $\alpha$

图1. 参数 $\alpha$ 的几何意义

2.4. 曲线的形状控制

由参数 $\alpha$ 的几何意义可知，表示 $\alpha \text{-}B$ 曲线的普通Bézier曲线的特征多边形将会随着 $\alpha$ 取值逐渐增大越加贴近 $\alpha \text{-}B$ 曲线的特征多边形。结合Bézier曲线具有的逼近性可推得， $\alpha \text{-}B$ 曲线会随参数 $\alpha$ 取值增大而越加逼近其特征多边形。取不同 $\alpha$ 值时的 $\alpha \text{-}B$ 曲线如图2所示，1~5号曲线分别代表 $\alpha$ 取 $0,\frac{1}{4},\frac{2}{4},\frac{3}{4},1$。特别地，线1为由 $P_0{P}_1\cdots P_6$ 所定义的六次Wang-Ball，线为由其所定义的Said-Ball曲线。

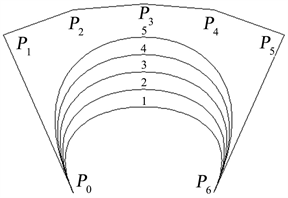
Figure 2. The $\alpha \text{-}B$ curves with different value of $\alpha$

图2. 取不同 $\alpha$ 值时的 $\alpha \text{-}B$ 曲线

2.5. 曲线的几何作图法

正如等式(5)所示， $\alpha \text{-}B$ 曲线可由Bézier曲线表示，且二者的特征点间的关系如式(7)所示。因此，当 $\alpha \text{-}B$ 曲线的特征点确定时，可先利用式(7)求出与之相关Bézier曲线的特征点，而后利用几何作图法，经过六级递推，所得终点即为 $\alpha \text{-}B$ 曲线上的点。 $\alpha \text{-}B$ 曲线的几何意义如图3所示， $\alpha =1$， $t=\frac{1}{2}$， $P_0{P}_1\cdots P_6$ 为 $\alpha \text{-}B$ 曲线的特征多边形， $V_0{V}_1\cdots V_6$ 为与之相关的Bézier曲线的特征多边形。

Figure 3. The geometrical drawing method of $\alpha \text{-}B$ curve

图3. $\alpha \text{-}B$ 曲线的几何作图法

3. 介于Said-Ball和Bézier曲线之间的曲线

3.1. 基函数的构造与性质

定义3 对于任意 $t\in \left[0,1\right]$，称多项式

$\{\begin{array}{l}{c}_{0,6}\left(t\right)=\left(1-2\beta t+\beta t^2\right){\left(1-t\right)}^4\\ c_{1,6}\left(t\right)=\left(4+2\beta -6\beta t\right)t{\left(1-t\right)}^4\\ c_{2,6}\left(t\right)=\left(10+5\beta \right)t^2{\left(1-t\right)}^4\\ c_{3,6}\left(t\right)=20t^3{\left(1-t\right)}^3\\ c_{4,6}\left(t\right)=\left(10+5\beta \right)t^4{\left(1-t\right)}^2\\ c_{5,6}\left(t\right)=\left(4-4\beta +6\beta t\right)t^4\left(1-t\right)\\ c_{6,6}\left(t\right)=\left(1-\beta +\beta t^2\right)t^4\end{array}$， $t\in \left[0,1\right]$ (9)

为带参数 $\beta$ 的六次广义Ball基函数，将其简称为 $\beta \text{-}B$ 基，其中 $0\le \beta \le 1$。

$\beta \text{-}B$ 基特性如下：

特性1 非负性和规范性。即 $c_{i,6}\left(t\right)\ge 0\left(i=0,1,\cdots ,6\right)$ 且 ${\displaystyle \underset{i=0}{\overset{6}{\sum }}{c}_{i,6}\left(t\right)}=1$。

特性2 对称性。即 $c_{i,6}\left(t\right)=c_{6-i,6}\left(1-t\right),i=0,1,\cdots ,6$。

特性3 端点性质。

$\{\begin{array}{l}{c}_{0,6}\left(0\right)=1\\ c_{i,6}\left(0\right)=0,i=1,2,3,4,5,6\end{array};\{\begin{array}{l}{c}_{i,6}\left(1\right)=0,i=0,1,2,3,4,5\\ c_{6,6}\left(1\right)=1\end{array}$

$\{\begin{array}{l}{c^{\prime }}_{0,6}\left(0\right)=-\left(2\beta +4\right)\\ {c^{\prime }}_{1,6}\left(0\right)=2\beta +4\\ {c^{\prime }}_{i,6}\left(0\right)=0,i=2,3,4,5,6\end{array};\{\begin{array}{l}{c^{\prime }}_{i,6}\left(1\right)=0,i=0,1,2,3,4\\ {c^{\prime }}_{5,6}\left(1\right)=-\left(2\beta +4\right)\\ {c^{\prime }}_{6,6}\left(1\right)=2\beta +4\end{array}$

特性4 单峰性。在区间 $\left[0,1\right]$ 上，任意基函数有唯一最大值，具体验证可通过对基函数求导证明。

特性5 退化性。当 $\beta =0$ 时， $\beta \text{-}B$ 基转变成六次Said-Ball基；当 $\beta =1$ 时， $\beta \text{-}B$ 基转变成六次Bernstein基。

3.2. 曲线的构造及性质

定义4 给定特征点点 $Q_i\in R^d\left(d=2,3;i=0,1,\cdots ,6\right)$，称曲线

$q\left(t\right)={\displaystyle \underset{i=0}{\overset{6}{\sum }}{Q}_i}{c}_{i,6}\left(t\right)$， $t\in \left[0,1\right]$ (10)

为带形状参数 $\beta$ 的六次广义Ball曲线，为了便于下文称呼，在此简称其为 $\beta \text{-}B$ 曲线。

根据 $\beta \text{-}B$ 基所具有的特性，可推得 $\beta \text{-}B$ 曲线具有与 $\alpha \text{-}B$ 曲线相似的特性：

特性1 端点性质

$q\left(0\right)=Q_0$， $q\left(1\right)=Q_6$ ； $q^{\prime }\left(0\right)=\left(2\beta +4\right)\left(Q_1-Q_0\right)$， $q^{\prime }\left(1\right)=\left(2\beta +4\right)\left(Q_6-Q_5\right)$。

这说明 $\beta \text{-}B$ 曲线特征多边形的首末边相切，切点分别为多边形的首端点 $Q_0$ 与末端点 $Q_6$。

特性2 凸包性。

特性3 对称性。

特性4 几何不变性与仿射不变性。

3.3. 形状参数的几何意义

为分析参数 $\beta$ 变化时对曲线形状造成的影响，下面针对 $\beta \text{-}B$ 曲线中形状参数的几何意义进行讨论。

将 $\beta \text{-}B$ 基改写为

$\{\begin{array}{l}{c}_{0,6}\left(t\right)=B_{0,6}\left(t\right)+\frac{2-2\beta }{6}{B}_{1,6}\left(t\right)+\frac{1-\beta }{15}{B}_{2,6}\left(t\right)\\ c_{1,6}\left(t\right)=\frac{4+2\beta }{6}{B}_{1,6}\left(t\right)+\frac{4-4\beta }{15}{B}_{2,6}\left(t\right)\\ c_{2,6}\left(t\right)=\frac{10+5\beta }{15}{B}_{2,6}\left(t\right)\\ c_{3,6}\left(t\right)=B_{3,6}\left(t\right)\\ c_{4,6}\left(t\right)=\frac{10+5\beta }{15}{B}_{4,6}\left(t\right)\\ c_{5,6}\left(t\right)=\frac{4-4\beta }{15}{B}_{4,6}\left(t\right)+\frac{4+2\beta }{6}{B}_{5,6}\left(t\right)\\ c_{6,6}\left(t\right)=\frac{1-\beta }{15}{B}_{4,6}\left(t\right)+\frac{2-2\beta }{6}{B}_{5,6}\left(t\right)+B_{6,6}\left(t\right)\end{array}$ (11)

(11)式可用矩阵表示为

$c=NB$

其中

$c={\left(\begin{array}{cccc}{c}_{0,6}\left(t\right)& c_{1,6}\left(t\right)& \cdots & c_{6,6}\left(t\right)\end{array}\right)}^{\text{T}}$

$N=\left(\begin{array}{ccccccc}1& \frac{2-2\beta }{6}& \frac{1-\beta }{15}& 0& 0& 0& 0\\ 0& \frac{4+2\beta }{6}& \frac{4-4\beta }{15}& 0& 0& 0& 0\\ 0& 0& \frac{10+5\beta }{15}& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& \frac{10+5\beta }{15}& 0& 0\\ 0& 0& 0& 0& \frac{4-4\beta }{15}& \frac{4+2\beta }{6}& 0\\ 0& 0& 0& 0& \frac{1-\beta }{15}& \frac{2-2\beta }{6}& 1\end{array}\right)$

$B={\left(\begin{array}{cccc}{B}_{0,6}\left(t\right)& B_{1,6}\left(t\right)& \cdots & B_{6,6}\left(t\right)\end{array}\right)}^{\text{T}}$

若记

$Q=\left(\begin{array}{cccc}{Q}_0& Q_1& \cdots & Q_6\end{array}\right)$

则 $\beta \text{-}B$ 曲线可用矩阵表示为

$q\left(t\right)=QNB$ (12)

记

$V=\left(\begin{array}{cccc}{V}_0& V_1& \cdots & V_6\end{array}\right)$

若令

$q\left(t\right)=VB$ (13)

即用六次Bézier曲线来表示 $\beta \text{-}B$ 曲线，其中 $V_i\left(i=0,1,\cdots ,6\right)$ 为六次Bézier曲线的控制顶点。则由式(12)和(13)可得Bézier曲线与 $\beta \text{-}B$ 曲线的控制顶点之间的关系式

$V=QN$ (14)

即

$\{\begin{array}{ll}{V}_0=Q_0\hfill & (\text{a})\hfill \\ V_1=\frac{2-2\beta }{6}{Q}_0+\frac{4+2\beta }{6}{Q}_1\hfill & (\text{b})\hfill \\ V_2=\frac{1-\beta }{15}{Q}_0+\frac{4-4\beta }{15}{Q}_1+\frac{10+5\beta }{15}{Q}_2\hfill & (\text{c})\hfill \\ V_3=Q_3\hfill & (\text{d})\hfill \\ V_4=\frac{10+5\beta }{15}{Q}_4+\frac{4-4\beta }{15}{Q}_5+\frac{1-\beta }{15}{Q}_6\hfill & (\text{e})\hfill \\ V_5=\frac{4+2\beta }{6}{Q}_5+\frac{2-2\beta }{6}{Q}_6\hfill & (\text{f})\hfill \\ V_6=Q_6\hfill & (\text{g})\hfill \end{array}$ (15)

式(15)中(c)式可以改写为

$V_2=Q_1+\frac{1-\beta }{15}\left(Q_0-Q_1\right)+\frac{10+5\beta }{15}\left(Q_2-Q_1\right)$ (16)

式(15)中(e)式可以改写为

$V_4=Q_5+\frac{10+5\beta }{15}\left(Q_4-Q_5\right)+\frac{1-\beta }{15}\left(Q_6-Q_5\right)$ (17)

由式(15)中的等式(b)可知，边 $Q_0{Q}_1$ 上的点 $V_1$ 将其分成比值为 $2+\beta :1-\beta$ 的两部分；由式(15)中的等式(f)可知，边 $Q_3{Q}_4$ 上的点 $V_3$ 将其分成了比值为 $1-\beta :2+\beta$ 的两部分；由等式(16)可推得，点 $V_2$ 位于以 $\frac{1-\beta }{15}\left(Q_0-Q_1\right)$ 和 $\frac{10+5\beta }{15}\left(Q_2-Q_1\right)$ 为邻边的平行四边形的终点处；由等式(17)可推得，点 $V_4$ 位于以 $\frac{10+5\beta }{15}\left(Q_4-Q_5\right)$ 和 $\frac{1-\beta }{15}\left(Q_6-Q_5\right)$ 为邻边的平行四边形的终点处。参数 $\beta$ 的几何意义如图4所示，其中参数 $\beta$ 取0， $Q_0{Q}_1\cdots Q_6$ 和 $V_{0}V\cdots V_6$ 分别为 $\beta$ B曲线和表示 $\beta \text{-}B$ 曲线的Bézier曲线的特征多边形。

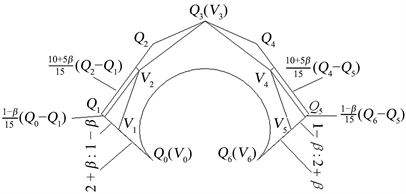
Figure 4. The geometric meaning of shape parameter $\beta$

图4. 参数 $\beta$ 的几何意义

3.4. 曲线的形状控制

由参数 $\beta$ 的几何意义可知，用于构造 $\beta \text{-}B$ 曲线的传统Bézier曲线的特征多边形将随着参数 $\beta$ 的增大而愈加贴近 $\beta \text{-}B$ 曲线的特征多边形。因此，根据Bézier曲线所具有的逼近性可知， $\beta \text{-}B$ 曲线将随着参数 $\beta$ 取值的增大，越加逼近其特征多边形。取不同 $\beta$ 值的 $\beta \text{-}B$ 曲线如图5所示，图中1~4号曲线分别为参数 $\beta$

等于 $0,\frac{1}{3},\frac{2}{3},1$ 时的曲线形状。特别地，曲线1和曲线4分别为由 $Q_0{Q}_1\cdots Q_6$ 所定义的六次Said-Ball和Bézier曲线。

Figure 5. The $\beta \text{-}B$ curves with different value of $\beta$

图5. 取不同 $\beta$ 值时的 $\beta \text{-}B$ 曲线

3.5. 曲线的几何作图法

正如等式(13)所示， $\beta \text{-}B$ 曲线可由传统Bézier曲线表示，并且二者的特征点间的联系如式(15)所示。由此可知，当 $\beta \text{-}B$ 曲线的特征点给定时，可以先利用等式(15)求得表示它的传统Bézier曲线的特征点，而后利用几何作图法，经过六级递推，所得最终点即为 $\beta \text{-}B$ 曲线上的点。 $\beta \text{-}B$ 曲线的几何作图法如图6所示。其中 $\beta =0$， $t=\frac{1}{2}$， $Q_0{Q}_1\cdots Q_6$ 为 $\beta \text{-}B$ 曲线的特征多边形， $V_{0}V\cdots V_6$ 为表示 $\beta \text{-}B$ 曲线的Bézier曲线的特征多边形。

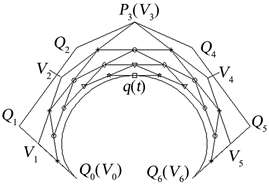
Figure 6. The geometrical drawing method of $\beta \text{-}B$ curve

图6. $\beta \text{-}B$ 曲线的几何作图法

4. 结束语

本文提出了的两种曲线构造方法，前者以六次Wang-Ball与Said-Ball曲线为特例，后者以六次Said-Ball和Bézier曲线为特例。由于形状参数的引入，二者皆能够在特征点确定的情况下，通过改变各自的形状参数的取值来调整曲线的形状与位置，进而分别得到介于六次Said-Ball和Wang-Ball曲线之间以及介于六次Said-Ball和Bézier曲线之间的无数条中间曲线。与文献 [6] 和文献 [7] 中提及的曲线构造方法相比，本文中的两组基函数的都为显式表示，并且结构更加精简。除此之外，文中提及的中间曲线只需通过增减形状参数的数值即可得到，求取也相对简单，并且这些曲线数量也是无限的。文中的形状参数均具有明确的几何意义，因此可以通过简单地选择参数值来构造相应中间曲线。

下一步的研究工作是构造出介于一般的n次Wang-Ball和Said-Ball曲线之间以及介于Said-Ball和Bézier曲线之间的中间曲线，并研究这些不同次数的中间曲线之间的关系。

基金项目

国家自然科学基金(11761008)；江西省自然科学基金(20161BAB211028)；江西省教育厅科技项目(GJJ160558)。