基于ARIMA模型下猪后腿肉(带皮)价格的预测

Prediction of the Price of Pork Ham (With Skin) Based on the ARIMA Model

摘要: 近期的新冠肺炎疫情和非洲猪瘟疫情对我国生猪存栏量均有所影响，猪肉价格随之上涨。为探究猪肉价格近期的变化趋势以及预测其未来走势，本文依据时间序列相关理论，使用ARIMA模型，对我国2020年4月5日至2022年4月15日期间的猪后腿肉(带皮)的市场零售价格数据进行拟合，建立了该价格的时间序列模型，并预测了未来4期的发展趋势。使用R语言统计软件进行编程，结果表明，原序列一阶差分后为平稳非白噪声序列，ARIMA (1, 1, 0)可以较好地拟合原序列，且通过了模型及参数的显著性检验。使用该模型对猪后腿肉(带皮)的市场价格进行短期预测，结果显示，未来4期的猪后腿肉(带皮)的市场价格呈现缓慢上涨的趋势。

Abstract: The recent COVID-19 and African swine fever outbreaks have both affected the stock of live pigs in my country, and pork prices have risen accordingly. In order to explore the recent trend of pork price changes and predict its future trend, this paper uses the ARIMA model based on time series correlation theory to analyze the pork ham (with skin) from April 5, 2020 to April 15, 2022 in our country. The market retail price data is fitted, the time series model of the price is established, and the development trend of the next 4 periods is predicted. Using R language statistical software for programming, the results show that the original sequence is a stationary non-white noise sequence after the first-order difference, ARIMA (1, 1, 0) can fit the original sequence well, and it has passed the significance of the model and parameters test. Using this model to make a short-term forecast of the market price of pork ham (with skin), the results show that the market price of pork ham (with skin) in the next 4 periods will show a slow upward trend.

1. 引言

2019年底出现的新型冠状病毒肺炎(Corona Virus Disease 2019, COVID-19)和2018年下半年出现的非洲猪瘟两场疫情对我国的经济和社会发展等各个方面都造成了巨大的影响。其中，猪肉作为中国的主要肉类消费品之一，由于生猪的存栏量下降 [1]，且销售环节存在更多的障碍与困难，所以猪肉的批发价格和市场零售价格都呈现上涨变化。目前，疫情仍未完全消失，所以猪肉的价格仍处于较大的波动之中。

目前对于我国农产品价格的预测研究，通常以生猪或活鸡的价格作为研究对象，较为常见的预测模型有VAR模型、ARIMA模型、GARCH模型等。如张瑞荣等 [2] 运用了两种时间序列模型(ARDL、ARIMA)来对比研究活鸡等价格的波动规律，预测未来价格走势；喻开志等 [3] 建立了VAR模型，研究了猪瘟疫情爆发后猪肉价格对鸡肉价格的影响；孙志华等 [4] 使用XGBoost模型得到了未来五年我国生猪存栏量和猪肉产量的预测值。研究表明，使用ARIMA模型研究目前猪肉价格的走势是恰当的，且新冠肺炎疫情和非洲猪瘟疫情的确会对生猪存栏量和猪肉价格产生影响。

本文意在研究猪肉价格在未来几周内的变化情况，考虑到各个部位的猪肉价格在同一时期内的上涨或下降情况和幅度均有较高的正相关性，为方便研究，本文选取了猪后腿肉(带皮)的价格数据作为研究对象，以此来说明猪肉价格在整体上的变化情况。

2. 研究背景及意义

2.1. 猪肉市场现状

新冠肺炎疫情于2019年12月出现在我国范围内，非洲猪瘟于2018年8月在我国发现疫情，受“双疫情”的影响，我国生猪存栏量急剧下滑，猪肉产量不足 [5]，从而生猪以及猪肉价格上涨 [1]。2020年前期，由于新冠肺炎疫情的爆发，人们对猪肉的需求量减少，从而猪肉价格出现短暂时间内的下降。随着抗疫工作的进一步展开，猪肉的价格基本处于一种波动上升的阶段 [5]。截至目前，疫情还未完全过去，猪肉的价格仍处于较大波动之中。

同时，考虑到中国的实际国情，21世纪以来，我国畜牧业的发展也处于困境之中 [6]。由于人口老龄化和农村常住人口的锐减等客观因素，畜牧业的劳动力也呈现下降趋势。目前，对于从事畜牧行业的人群来说，畜禽的疫病问题也不可忽视。养殖成本的增加、疫病几率的上升、质量安全无法得到完全保证，这些问题都会直接或间接地导致从事畜牧业的门槛上升，进而人员数量降低，则有关肉类的价格也会随之上升。生猪行业作为畜牧业的组成部分之一，不可避免的会受到上述以及更多原因的影响，所以猪肉的价格并不稳定，且易出现价格上涨的现象。

2.2. 目的与意义

生猪产业为我国畜牧业的重要组成部分以及居民生活的必需品，与人民生活息息相关，在日常生活中有重要地位 [7]。猪肉价格的不稳定不可避免地会导致人民生活受到一定程度的影响，研究猪肉价格的发展态势不仅有助于从事畜牧养殖业的工作者明晰生猪产业目前的发展情况，同时对居民们的饮食方面也可以给予一定程度上的指导。

所以探究后疫情时代猪肉价格的波动情况，预测未来一段时间的猪肉价格是很有必要的。由于猪肉各部位的价格变动的整体性和统一性，本文选用猪后腿肉(带皮)的市场零售价格作为代表研究对象来完成研究目的。

3. 相关理论

3.1. 数据来源

本文数据来自平台：全国重点农产品市场信息平台。网址为：http://ncpscxx.moa.gov.cn/product-web/#/sing?headingIndex=true&item=1。

根据该网站的公开数据，本文选取了2020年4月5日至2022年4月15日期间，每个月的5号、15号、25号的猪后腿肉(带皮)的市场零售价格数据(单位：元/公斤)作为研究数据，来预测未来4期的价格。

3.2. 研究方法

本文将上述时间段内猪后腿肉(带皮)每个月的5号、15号、25号的价格数据分别作为每期数据，使用时间序列ARIMA模型对猪肉价格进行短期预测。为方便表示，将2020年4月5日的数据记为“1”，2020年4月15日的数据记为“2”，……以此类推，共有74期数据。

3.3. 理论基础

求和自回归移动平均(Autoregressive Integrated Moving Average)模型，简称ARIMA模型，是于1970年由BOX和Jenkins提出的一种用于对时间序列进行预测的模型，主要用于无季节效应的非平稳时间序列。具有以下结构 [8]：

$\{\begin{array}{l}\Phi \left(B\right){\nabla }^d{x}_t=\Theta \left(B\right){\epsilon }_t\\ E\left({\epsilon }_t\right)=0,Var\left({\epsilon }_t\right)={\sigma }_{\epsilon }^2,E\left({\epsilon }_t{\epsilon }_s\right)=0,s\ne t\\ E\left(x_s{\epsilon }_t\right)=0,\forall s<t\end{array}$ (1)

式中， ${\nabla }^d={\left(1-B\right)}^d$ ； $\Phi \left(B\right)=1-{\varphi }_{1}B-\cdots -{\varphi }_p{B}^p$，为平稳可逆ARMA (p, q)模型的自回归系数多项式； $\Theta \left(B\right)=1-{\theta }_{1}B-\cdots -{\theta }_q{B}^q$，为平稳可逆ARMA (p, q)模型的移动平均系数多项式。其中p为自回归阶数，d为平稳化处理的最少差分次数，q为移动平均阶数。

ARIMA (p, d, q)建模流程图 [8] 如图1所示。

4. 模型的建立与求解

4.1. 数据预处理

对于所要研究的74期数据，其中有8期数据为缺失值，为2021年1月25日、2月5日、2月15日、

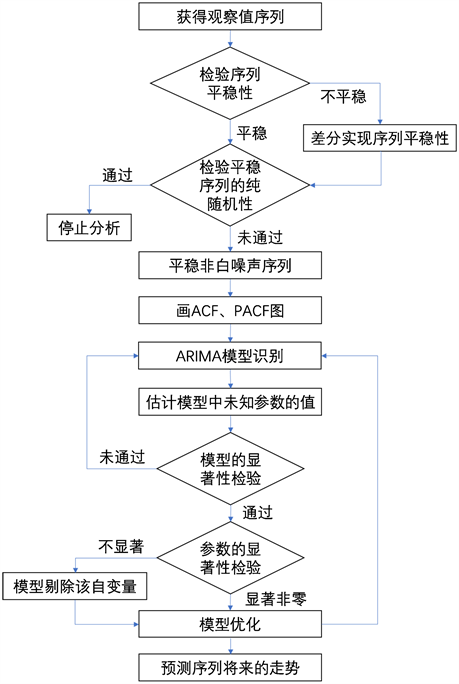
Figure 1. ARIMA model modeling process flow chart

图1. ARIMA模型建模过程流程图

4月5日、8月5日、10月25日、2022年1月15日、4月15日的猪后腿肉(带皮)的价格数据。本文使用K-最近邻估算(K-NN)算法 [9] 实现数据插补，取k = 3。

补全数据后，首先需要对所要研究的观察值序列进行平稳性检验，常用的方法有图检验和ADF检验。若平稳，则可进行下一步；否则，需要对序列进行差分，直至平稳，差分次数记为d。之后，对上述平稳序列进行纯随机性检验，若为非纯随机序列，则可进行下一步；否则，认为该序列的未来发展不可预测，故可以停止分析。关于平稳性检验和纯随机性检验的更多相关理论详见参考文献8。

4.1.1. 平稳性检验

时间序列的平稳性是指宽平稳性，常见的检验方法有两种：图检验和构造检验统计量进行假设检验。绘制此74组猪后腿肉(带皮)价格数据的时序图，见图2。

图2的时序图显示，从第32期至第45期，即2021年2月15日至2021年6月25日期间，猪后腿肉(带皮)的价格呈现断崖式下跌，由此可根据图检验法判断该序列不平稳。另外，使用构造检验统计量的

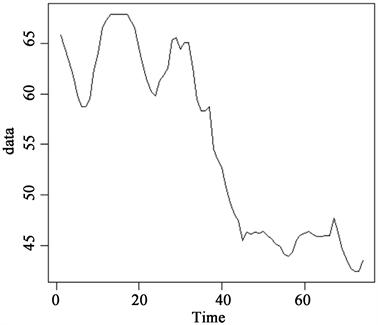
Figure 2. Timing diagram of the original sequence

图2. 原序列的时序图

方法进行平稳性检验，计算出P值= 0.09487，故原序列不平稳，下面对其进行差分化处理。

一阶差分后的时序图如图3所示。由一阶差分后序列的平稳性检验的P值= 0.01799可得，一阶差分后序列达到平稳，故将模型ARIMA (p, d, q)中的d定为1。

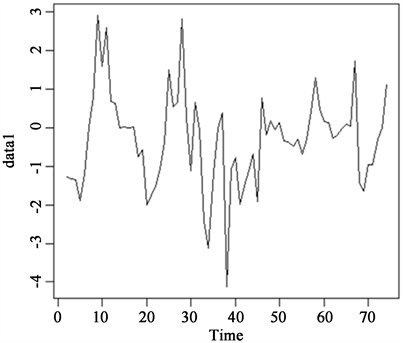
Figure 3. Timing diagram of the sequence after first order difference

图3. 一阶差分后序列的时序图

4.1.2. 纯随机性检验

纯随机序列又称白噪声序列，对于一个平稳时间序列，如果它是一个白噪声序列，则说明该序列的信息已被全部提取了出来，无法对其进行预测，故没有继续研究下去的意义。

对一阶差分后的平稳序列用Q_LB统计量做纯随机性检验，检验结果如表1所示。

由于P值小于显著性水平α = 0.05，所以拒绝该序列为纯随机序列的原假设，即一阶差分后的猪后腿肉(带皮)价格序列为平稳非白噪声序列，可继续分析。

Table 1. White noise test results for sequences after first-order difference

表1. 一阶差分后序列的白噪声检验结果

4.2. 模型的识别与建立

为选择合适的模型来拟合序列，需要画出该序列的样本自相关图及偏自相关图，根据图中所呈现的样本自相关系数和偏自相关系数的拖尾性及截尾性来选择模型的类型及阶数p和q，之后估计模型中未知参数的值。其中，拖尾性是指：滞后任意k阶的自相关系数 ${\rho }_k$ 始终有非零取值，不会在k大于某个常数后恒为0；截尾性是指：滞后k阶的偏自相关系数 ${\varphi }_{kk}$ 在k > p时恒等于0 [8]。

根据所选取时间段内的猪后腿肉(带皮)的价格数据，算出其一阶差分后数据的自相关系数与偏自相关系数，分别见表2、表3。

Table 2. The autocorrelation coefficient of the series after the first difference

表2. 一阶差分后序列的自相关系数

Table 3. Partial autocorrelation coefficient of the series after the first difference

表3. 一阶差分后序列的偏自相关系数

下面根据表2中的自相关系数和表3中的偏自相关系数画出样本自相关系数图和偏自相关系数图，分别见图4、图5，根据其所呈现出的拖尾性及截尾性来选择模型的类型及阶数p和q，之后估计模型中未知参数的值。

由一阶差分后序列的自相关图(图4)与偏自相关图(图5)可看出，自相关系数呈现阶梯式缓慢下降的现象，且6、10阶的自相关系数也与两倍标准差很接近，故判断为拖尾；而各阶的偏自相关系数都在两倍标准差范围内，故判断为截尾。又因为原序列差分1次后平稳，故选用ARIMA (1, 1, 0)模型进行拟合。

4.3. 参数估计与模型检验

在选择了合适的ARIMA (p, d, q)模型后，需对模型中的未知参数进行估计，从而确定该模型的口径。之后，需要对模型的显著性进行检验，若通过模型的显著性检验，则称该模型是有效的，那么接下来可

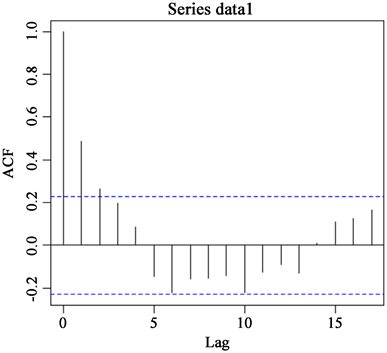
Figure 4. Autocorrelation lot of series after first difference

图4. 一阶差分后序列的自相关图

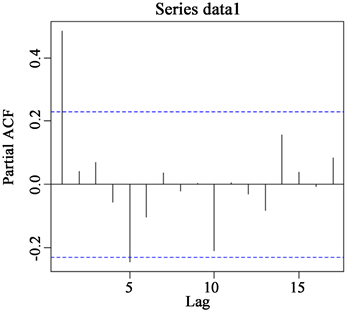
Figure 5. Partial autocorrelation plot of series after first-difference

图5. 一阶差分后序列的偏自相关图

用它来预测该序列的未来发展趋势；否则，该模型不能用于未来的预测，需重新进行模型识别。通过模型检验后，需要对模型中的参数进行显著性检验。对于每个未知参数来说，若该参数不显著非零，需将该参数对应的自变量从模型中剔除，再构造结构更精简的拟合模型。当模型和参数的显著性检验均通过时，该模型才可用来预测猪后腿肉(带皮)未来的价格。

4.3.1. 参数估计

对选用的ARIMA (1, 1, 0)模型使用“CSS-ML”估计(条件最小二乘与极大似然估计混合方法)，确定该模型的口径，结果如表4所示。

故模型表达式为：

$x_t=54.83486+0.5209x_{t-1}+{\epsilon }_t$ (2)

Table 4. Caliber of the ARIMA (1, 1, 0) model

表4. ARIMA (1, 1, 0) 模型的口径

4.3.2. 模型检验

确定了模型的口径后，下面分别对模型和参数的显著性进行检验：

残差序列白噪声检验结果如表5所示：

Table 5. Residual series white noise test results

表5. 残差序列白噪声检验结果

P值均 > α，接受原假设，说明拟合模型显著有效。

2) 参数的显著性检验：

用“CSS-ML”估计方法，得参数检验结果如表6所示：

Table 6. Parametric test results

表6. 参数检验结果

P值均 < α，拒绝原假设，说明每一个未知参数都显著非零，故不需去除自变量，使用该模型用于对序列未来的预测即可。

由以上分析可知，本文所选取的ARIMA (1, 1, 0)模型通过了模型的显著性检验，其中的各参数也通过了参数的显著性检验，所以使用ARIMA (1, 1, 0)模型来拟合2020年4月5日至2022年4月15日期间的猪后腿肉(带皮)的价格数据、并用此模型来预测猪后腿肉(带皮)未来一段时间的价格是恰当的。

5. 预测结果与分析

经过上述步骤的处理，选用的ARIMA (1, 1, 0)模型通过了检验，可用此模型来预测原序列未来的发展趋势。下面用它来预测未来4期的值，预测值见表7，预测图及个性化预测图分别见图6、图7。

其中，蓝色实线为实际值所连成的线，蓝色点为未来4期的预测值，深灰色区域为95%置信区间，浅灰色区域为80%置信区间，横轴代表期数，纵轴代表猪后腿肉(带皮)各期的价格(单位：元)。

从图6看，未来4期的猪后腿肉(带皮)的价格发展趋势为缓慢上升，即虽然价格上涨，但上涨速率较为缓慢，可认为该段时间内价格较为稳定，没有过大的波动。

Table 7. Predicted values for the next 4 periods and their 95% confidence intervals

表7. 未来4期的预测值及其95%置信区间

Figure 6. Forecast chart for the next 4 periods

图6. 未来4期的预测图

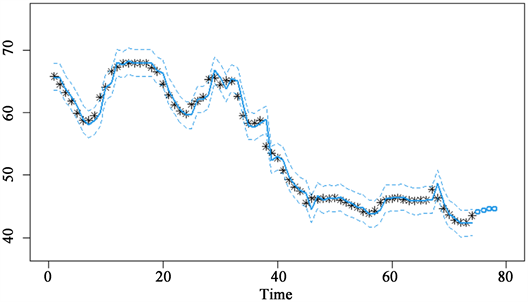
Figure 7. Personalized forecast chart for the next 4 periods

图7. 未来4期的个性化预测图

其中，黑色星号为实际值，蓝色实线为拟合线，蓝色虚线区域内为拟合值的95%置信区间，蓝色空心点为未来4期的预测值，横轴代表期数，纵轴代表猪后腿肉(带皮)各期的价格(单位：元)。

从图7中看，模型拟合线偏离价格实际值的程度不大，故模型和序列真实值的拟合度较高，拟合效果较好。

通过模型ARIMA (1, 1, 0)的预测结果可知，未来4期的猪后腿肉(带皮)的价格发展趋势呈现缓慢上升趋势。这意味着未来一个月左右的猪后腿肉(带皮)的价格将在目前的价格基础上呈上涨态势；但同时由于上升的斜率是较缓的，所以应该不会面临一个价格暴涨的局面。由于猪肉各部位的价格变化情况具有整体性，所以可认为，猪肉的价格变动情况与猪后腿肉(带皮)价格的变动情况相类似，即在未来一个月时间中，猪肉的价格将呈现一个缓慢上升的态势。

6. 讨论

本文使用ARIMA模型，对猪后腿肉(带皮) 2020年4月5日至2022年4月15日的价格数据完成了建模与预测，具有较为显著的短期预测效果。预测结果显示，未来4期的猪后腿肉(带皮)的价格会较为缓慢地上涨，但应该会保持在50元/公斤的水平线的下方。由于猪肉各部位价格有较高的正相关性，所以猪肉价格的变化状况整体上与猪后腿肉(带皮)的价格变化情况类似。造成这种现象的原因可能是近期我国新冠疫情有反复之势，但同时也很好地控制住了发展局面，所以虽然存在猪肉价格上涨的可能性，但并不会出现猪肉价格暴涨的局面。

为简化建模过程，本文选择了一元时间序列来模拟猪后腿肉(带皮)的价格，但由于实际情况的复杂性，该价格可能与其他多个变量有关，故可使用多元时间序列来尝试实现优化。

此外，本文坚持从真实数据出发，依照ARIMA理论，找到了适合拟合真实数据的模型，保证了分析的真实性和可靠性 [10]。

基金项目

校级大学生创新创业训练计划项目XJ20200063。