基于目标辐射的被动测距方法

Passive Ranging Method Based on Target Radiation

摘要: 为了满足现代战争的需要，对来袭目标的精确测量显得尤为重要。当前应用的主流探测手段是雷达探测。由于雷达为主动探测，在探测的过程中会暴露自己，很容易被敌方反辐射武器针对，而且武器隐身技术成为当下的主流，雷达的局限性愈发明显。红外被动测量方法则不然，任何有温度的物体都会辐射能量，利用此特性，既不会暴露自己，也可以很精确地获取来袭目标的距离温度信息。基于上述背景，本文利用美国空军大气传输软件MODTRAN生成不同温度、距离下目标在不同波段的透过率数据，利用Matlab计算出不同温度、距离下目标所对应的辐照度，通过对辐照度数据的分析与仿真，本文提出了红外目标的温度线和距离线概念，利用目标温度线及距离线，提出了两种新的红外被动测距方法。

Abstract: In order to meet the needs of modern war, it is very important to accurately measure the incoming target. Radar detection is the main detection method currently used. As radar is active detection, it will expose itself in the detection process, and it is easy to be targeted by enemy anti-radiation weapons. Moreover, weapon stealth technology has become the mainstream at present, and the limitations of radar are increasingly obvious. The infrared passive measurement method is different. Any object with temperature will radiate energy. With this feature, it will not expose itself, and also can obtain the distance and temperature information of the incoming target very accurately. Based on the above background, this paper generated transmittance data under different temperatures and distances from target at different wavelengths by Modtran, and used Matlab to calculate the target’s irradiance under different temperatures and distances. Through the analysis of the irradiance data and simulation, this paper puts forward the concept of lines to the target temperature and the distance. A new infrared passive ranging method is developed by using target temperature line and range line. Secondly, the correlation analysis of the irradiance of the target in the spectrum is carried out, and it is found that the irradiance ratio of 9.0~9.2 and 9.2~9.4 bands is independent of temperature and strongly correlated with distance. Based on this finding, a new passive ranging method is proposed in this paper. The combination of the above two methods can improve the accuracy, fault tolerance and robustness of ranging.

1. 研究内容

本文研究内容分两部分，第一部分如下：利用MODTRAN仿真得到不同温度、不同距离下的透过率，将被测红外目标等效黑体，通过普朗克公式计算出目标的辐照度，选择两个辐射能量较多的窗口作为工作波段，将两个波段测得的辐照度作为两个相关变量，对同一温度不同距离下的目标进行线性拟合，得到目标的温度线，对同一距离不同温度下的目标进行拟合，得到目标的距离线，温度线拟合为直线，距离线拟合为二次曲线，通过已知温度线和距离线的系数建立了双波段测温模型，进而求解未知目标的距离。具体过程如下：1) 测量目标在两个波段的辐照度。2) 通过两个波段辐照度的比值在已知温度线模型中进行比对，找出目标的温度范围。3) 将双波段辐照度代入已知温度范围的距离线模型中，解算出目标的距离 [1]。

第二部分的主要内容为利用目标不同波段辐照度的相关性，寻找一条在一定范围内的与目标温度无关的距离线，这样就可以不用关心目标的温度，直接求解目标的距离。通过对不同窄波段的辐照度值与温度的相关性分析，发现当温度大于450 K时，9.2~9.4 μm与9.4~9.6 μm波段的辐照度比值在一定温度范围内近乎保持不变，即这两波段的比值与温度无关，但与距离相关，因此可以通过这两波段的比值建立双波段测距模型 [2]。

将上述两种测距模型结果的交集作为最终的输出结果，便可以提高模型的精度以及稳定性。下面将分别对两种测距模型的具体方法进行论述。

2. 研究方法

2.1. 测距方法1

1) 通过接收目标双波段辐照度的多组数据点，对数据点线性拟得出温度线斜率从而确定目标的温度范围。

2) 根据目标的温度范围选取此温度范围对应的距离线。

3) 通过数据点与距离线的相对关系从而确定目标与观测点间的距离。具体判别方法为：将数据点横坐标带入距离线的回归方程，从而判断数据点与距离线的关系，通过数据点到相邻两距离线距离值的大小对两线间的距离进行填充，由此确定更加精确的距离。

为实现上述目的，本文采取的技术方案为 [3]：

1a) 截取不同的波带

采集待测目标 $t=\left\{t_i|i=1,2,\cdots ,N\right\}$ 辐射的红外光波长 $\lambda =\left\{{\lambda }_i|i=1,2,\cdots ,N\right\}$，其中N ≥ 1；

1b) 计算辐照度

对步骤(1a)中截取的两个不同波带分别进行逐线积分，获取两个波带上不同待测目标t和传输距离对应的多组光辐射能量E₁和E₂，其中E₁为λ₁~λ₂ μm波带的光辐射能量，E₂为λ₃~λ₄ μm波带的光辐射能量；

1c) 估计目标温度

将步骤(1b)中获取的光辐射能量E₁和E₂进行拟合，得到线性关系 $E_2=k{E}_1+b$，其中，k表示取决于目标温度的系数，根据k值的大小可以估计目标自身的温度；E₁和E₂分别对应两个窄波带的光辐射能量；b表示该线性关系的截距；

1d) 建立目标距离线模型

同步骤(1c)相同，将(1b)中获取的光辐射能量E₁和E₂进行二次拟合，E₁和E₂对应的是一定温度范围下同一距离不同温度的光辐射能量，得到 $E_1=k_1{E}_2+k_2{E}_2+c$ 、 $k_1$ 、 $k_2$ 和c便是距离模型系数；

1e) 解算距离

通过传感器获取未知目标的光辐射能量E₁和E₂，通过(1c)所示方法估计未知目标温度范围，然后截取温度范围在(1d)中对应已知的距离线模型，将未知目标E₁和E₂带入距离线模型中即可解出目标对应的距离。

2.2. 测距方法2

1) 通过接收目标双波段辐照度的多组数进行据点，对数据点线性拟得出温度线斜率从而确定目标的温度范围 [4]。

2) 根据目标的温度范围选取此温度范围对应不同距离的辐照度比值范围。

3) 获取目标9.2~9.4 μm与9.4~9.6 μm的辐照度比值，与(2.2)中不同距离对应的比值范围进行匹配，进而确定目标与观测点的距离。

实现上述目的技术方案同测距方法一类似，如下：

2a) 截取特定的波带

同1.1类似，截取9.2~9.4 μm与9.4~9.6 μm波带作为待测波段；

2b) 计算辐照度

同1.2所示方法相同，计算9.2~9.4 μm与9.4~9.6 μm对应的辐照度E₁和E₂，通过MODTRAN和Matlab仿真出不同距离下E1和E2的辐照度，供下文标定使用；

2c) 估计目标温度

此处估计目标温度同(1c)完全相同，如果对测距精度要求不高或者目标的温度可以确定在一定的范围内的情况，此过程可以省略；

2d) 建立目标距离线模型

使用(2b)仿真得到的不同距离下的辐照度建立距离线模型，距离线拟合直线为 $E_1=k{E}_2+b$，其中k、b为距离系数；

2e) 解算距离

通过传感器获取未知目标的光辐射能量E₁和E₂，通过(2c)所示方法估计未知目标温度范围，然后截取温度范围在(2d)中对应已知的距离线模型，将未知目标辐照度E₁和E₂带入距离线模型中即可解出目标对应的距离。

3. 实验结果

3.1. 仿真实验条件

本文的实验环境为Windows 8.0系统，处理器型号为Intel(R)Core(TM)i5-3230M CPU@2.60GHZ，显存4G，64位操作系统上使用matlab r2018b进行仿真。大气透过率计算软件：pcmodwin4.0。数据拟合软件：IMB-SPSS-Statistics-25。

3.2. 实验方案及结果

3.2.1. 测距方法1

对于测距方法1，实验方案如下：

截取3.2~3.4 μm与8.2~8.4 μm两个窄波带作为工作窗口，以8.2~8.4 μm波段对应的辐照度为自变量，3.2~3.4 μm对应的辐照度为因变量，拟合出目标600~1000 K的温度线，温等线图及其模型系数如图1和表1：

Figure 1. 600~800 K isotherm

图1. 600~800 K等温线图

然后将不同温度线上对应的同一距离的数据点标记，然后对这些数据点进行拟合，拟合后的线我们称之为距离线，相较于大温度跨度，小温度跨度大拟合出的距离线与实际数据更加贴合，所以本文将温度跨度设置为100 K，也就是说温度线可接受的误差为100 K。经过反复实验，对低温目标适合用二项式对距离线进行拟合，拟合系数如下表，调整后的R2为0.999，达到预期效果。

Table 1. 2:1:15 Km isotherm coefficient

表1. 2:1:15 Km等温线系数

部分高温距离线及其模型系数分别如图2、图3、表2、表3：

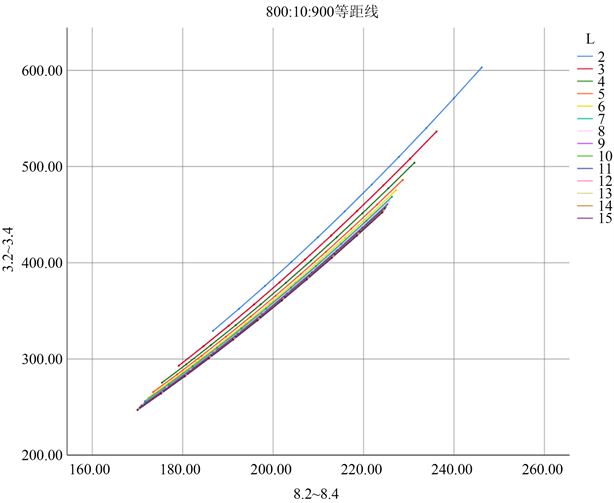
Figure 2. Isometric line of 800~900 K target

图2. 800~900 K目标的等距线

Table 2. 800:10:900 K isometric coefficient

表2. 800:10:900 K等距系数

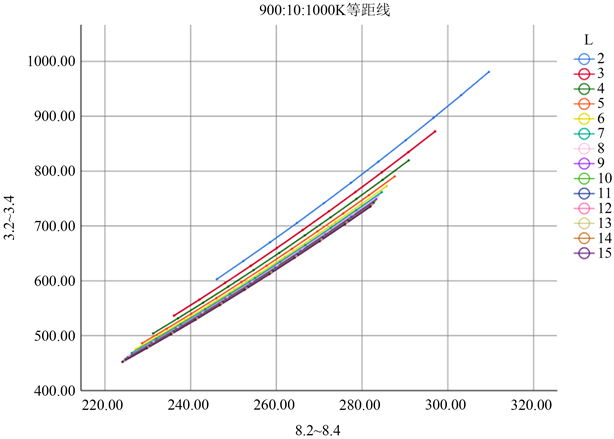
Figure 3. 900:10:1000 K isometric line

图3. 900:10:1000 K等距线

Table 3. 900:10:1000 K isometric coefficient

表3. 900:10:1000 K等距系数

3.2.2. 测距方法2

对于方法2，实验方案以及结果如下：

本文对不同窄波段的辐照度值相关性分析，发现一定温度大于450 K时，9.2~9.4 μm与9.4~9.6 μm波段的辐照度比值在一定温度范围内近乎与温度无关，但与距离相关，此现象对高温、远距离目标极为明显，由此可以根据目标辐照度直接确定目标距离。通过仿真，得到450~1150 K、2~20 Km对应的辐照度比值，将双波段的比值按100 K等温度分开，为不失一般性，分别对距离为2 Km、5 Km、10 Km、18 Km为中心的数据进行仿真，对不同距离下的辐照度比值进行整理，选取18 Km为数据中心，1 Km为距离间隔，进行理论展示，整理结果如表4~10：

Table 4. 450~550 K dual-band ratio data

表4. 450~550 K双波段比值数据

Table 5. 550~650 K dual-band ratio data

表5. 550~650 K双波段比值数据

Table 6. 650~750 K dual-band ratio data

表6. 650~750 K双波段比值数据

Table 7. 750~850 K dual-band ratio data

表7. 750~850 K双波段比值数据

Table 8. 850~950 K dual-band ratio data

表8. 850~950 K双波段比值数据

Table 9. 950~1050 K dual-band ratio data

表9. 950~1050 K双波段比值数据

Table 10. 1050~1150 K dual-band ratio data

表10. 1050~1150 K双波段比值数据

4. 结果验证

用MODTRAN仿真温度为980 K、距离观测者10 Km左右的目标的辐照度数据，各窄波段数据如下表11：

Table 11. 10 Km verification data

表11. 10 Km验证数据

1) 首先通过3.2~3.4 μm、8.2~8.4 μm两个窄波段的两组数据进行拟合，斜率为9.908，与温度系数表1进行匹配，目标温度范围为950~1050 K。

2) 将10 Km的模拟辐照度数据与950~1050 K的距离线在同一坐标轴下进行比较，根据上述距离线拟合系数，9 Km的距离线表达式为：y = 4.962x − 661.933，10 Km距离线表达式为：y = 4.943x − 658.55，11 Km的距离线表达式为：y = 4.928x − 655.902，将数据点(271.1297, 681.3614)带入各表达式中，求取数据点到距离线的距离，经计算数据点介于10 Km与11 Km距离线之间，且距10 Km距离线0.2827，距11 Km距离线26.5957，所以目标距离近似为10 Km。

3) 根据探测方法二，计算得9.2~9.4 μm与9.4~9.6 μm波段的辐照度比值为1.248，由1)可知，目标的温度范围为950~1050，将1.248与950~1050 K对应的辐照度比值表进行匹配 [5]，如下表12：

Table 12. 950~1050 K dual-band ratio data

表12. 950~1050 K双波段比值数据

1.248介于1.247与1.250之间，所以可知目标距离为10 Km。

4) 综合探测方法一与探测方法二的结果，可得两种结果的交集为10 Km，所以最终确定目标距离观测点的距离为10 Km，验证完毕。

5. 结论

本文基于双波段测距提出了距离线概念，通过温度线确定目标温度，已知目标温度后进而可以有效提高距离线模型的准确度。其次本文首次发现9.2~9.4 μm、9.4~9.6 μm两波段比值与温度的无关性以及与距离的强相关性。两种测距模型各有利弊，但可以互补，通过距离线模型测距适合近距离测距，相对远距离来说，近距离辐照度变化随距离变化幅度大，远距离则不然，随着距离的不断增大，辐照度随距离变化的幅度非常小，不足以引起距离线模型的变化，距离线近乎保持不变。对高温远距离目标进行双波段比值测距，9.2~9.4 μm、9.4~9.8 μm双波段辐照度比值几乎与目标温度毫无关系，且与距离有非常强的相关性，但随着温度的降低，这种相关性逐渐变弱，当目标温度小于450 K时，这种相关性已不足以判断距离。综合仿真结果，将两种测距方法误差结合，误差完全控制在10%以内，对于高温目标，误差可以控制在5%以内，测距精度相较当前的行业精度有巨大提升。