一类离散FHN系统的分支控制

Bifurcation Control of the Discrete FHN System

摘要: 本文讨论了离散FHN系统中Neimark-Sacker分支的控制问题，主要设计了一类状态反馈控制器，该控制器不仅形式简单，而且可以不改变不动点的位置，精确有效地控制此类分支的临界值，从而实现分支发生的提前或延滞。

Abstract: This paper investigates the control of Neimark-Sacker bifurcation of the discrete FHN system. A kind of state feedback controller is designed, which not only has a simple form, but also accurately and effectively controls the critical value of such bifurcation without changing the position of the fixed point, so as to realize the advance or delay of the bifurcation.

1. 引言

分支是非线性系统具有代表性的复杂动力学行为，分支控制的研究受到许多国内外学者的关注 [1] [2] [3] [4] [5]。2017年Guo等人 [3] 采用非线性状态反馈控制法控制水轮机组频率恢复到额定频率，从而保证了电力系统正常运行。2019年，Akhtar等人 [4] 采用混合控制法，发现延迟Neimark-Sacker分支发生可调节生物种群中捕食者与被捕食者的密度，从而使生态系统种群保持一定的稳定状态。同年，Cheng等人 [5] 提出并分析了非线性状态反馈控制的SIR模型，考虑了隔离、疫苗接种和治疗等防控策略对减少传染病传播的影响，发现易感人群的规模对于根除传染病起着关键作用，这些研究结果对于制定合理有效的综合防控措施，预防控制以及消除传染病提供了理论基础。

本文主要研究了一类离散FitzHugh-Nagumo系统(简称离散FHN系统)的Neimark-Sacker分支控制问题。首先从理论上严格证明了Neimark-Sacker分支的存在性，其次在保持分支不动点位置的前提下，设计出一个简单有效的线性状态反馈控制器，使Neimark-Sacker分支发生的分支值减小或增大可以被精准控制，这些结果对于调节和控制生物神经元放电行为的研究有重要的理论参考价值。

2. 主要内容

考虑如下离散FHN系统 [6]

$f:\left(\begin{array}{c}x\\ y\end{array}\right)\to \left(\begin{array}{c}x+\delta \left(x-\frac{x^3}{3}-y+I\right)\\ y+\frac{\delta }{\tau }\left(ax+b-y\right)\end{array}\right)$ (1)

其中x为神经元细胞膜上的电压，y代表膜电压，参数I表示神经元受到的刺激强度， $b=I=0.3$， $a=1.8$， $\tau =0.8$， $\delta \left(\in \left(0,1\right)\right)$ 为分支参数。

2.1. 不动点及其Neimark-Sacker分支

由离散动力系统的定性与稳定性理论可知，系统(1)存在唯一的不动点 $Z_0=\left(0,0.3\right)$ ：当 $0<\delta <0.25$ 时，不动点 $Z_0$ 是稳定的；当 $0.25<\delta <1$ 时，不动点 $Z_0$ 是不稳定的；当 $\delta =0.25$ 时，不动点 $Z_0$ 是非双曲不动点，其特征值为 $\left\{0.96875-0.24804i,0.96875+0.24804i\right\}$。

运用分支理论，可得以下定理。

定理1：当分支参数 $\delta$ 逐渐增大，穿过临界值 ${\delta }_0=0.25$ 时，系统(1)的不动点 $Z_0=\left(0,0.3\right)$ 发生了Neimark-Sacker分支，即不动点 $Z_0$ 失去稳定性，在 $Z_0$ 的小邻域内生成了一族稳定的周期轨。

证明：令 $u=x$， $v=y-0.3$， $\alpha =\delta -0.25$，则系统(1)变为

$\left(\begin{array}{c}u\\ v\end{array}\right)\to \left(\begin{array}{cc}1.25& -0.25\\ 0.5625& 0.6875\end{array}\right)\left(\begin{array}{c}u\\ v\end{array}\right)+\left(\begin{array}{c}-\frac{0.25u^3}{3}+\alpha \left(u-\frac{u^3}{3}-v\right)\\ \alpha \left(2.25u-1.25v\right)\end{array}\right)$ (2)

选取线性变换矩阵 $T=\left(\begin{array}{cc}0.416025& 0.3669\\ 0.83205& 0\end{array}\right)$，令 $\left(\begin{array}{c}u\\ v\end{array}\right)=T\left(\begin{array}{c}U\\ V\end{array}\right)$，代入(2)可得

$\left(\begin{array}{l}U\\ V\end{array}\right)\to \left(\begin{array}{cc}0.96875& 0.24804\\ -0.24804& 0.96875\end{array}\right)\left(\begin{array}{l}U\\ V\end{array}\right)+\left(\begin{array}{c}G\left(U,V\right)\\ K\left(U,V\right)\end{array}\right)$ (3)

其中

$G\left(U,V\right)=\alpha \left(-0.1249999U+0.825525V\right)$,

$\begin{array}{c}K\left(U,V\right)=-0.2271283{\left(0.416025U+0.3669V\right)}^3+\alpha (-0.99215618U{}_{}{}^{}\\ -0.9085133{\left(0.416025U+0.3669V\right)}^3-0.125V)\end{array}$.

系统(3)的不动点(0, 0)的特征值为

${\lambda }_{1,2}\left(\alpha \right)=0.125\alpha -0.96875\pm i\sqrt{0.984375{\alpha }^2+0.4921875\alpha +0.0615234375}$,

${\left|{\lambda }_{1，2}\left(\alpha \right)\right|}^2={\alpha }^2+0.25\alpha +1$.

系统(3)满足：

$G\left(0,0\right)=0$, $K\left(0,0\right)=0$, $d={\frac{\text{d}\left|\lambda \left(\alpha \right)\right|}{\text{d}\alpha }|}_{\alpha =0}=0.125>0$,

$l=-\mathrm{Re}\left[\frac{\left(1-2\lambda \right){\bar{\lambda }}^2}{1-\lambda }{Q}_{11}{Q}_{20}\right]-\frac{1}{2}{\left|Q_{11}\right|}^2-{\left|Q_{02}\right|}^2+{\mathrm{Re}\left(\bar{\lambda }{Q}_{21}\right)|}_{\alpha =0}=-0.01763964<0$,

其中

$Q_{20}=\frac{1}{8}{\left(G_{UU}-G_{VV}+2K_{UV}+i\left(K_{UU}-K_{VV}-2G_{UV}\right)\right)|}_{\left(0,0\right)}=0$,

$Q_{11}=\frac{1}{4}\left(G_{UU}+G_{VV}+i\right){\left(K_{UU}+K_{VV}\right)|}_{\left(0,0\right)}=0$,

$Q_{02}=\frac{1}{8}{\left(G_{UU}-G_{VV}-2K_{UV}+i\left(K_{UU}-K_{VV}+2G_{UV}\right)\right)|}_{\left(0,0\right)}=0$,

$\begin{array}{c}{Q}_{21}=\frac{1}{16}{\left(\left(G_{UUU}+G_{UVV}+K_{UUV}+K_{VVV}\right)+i\left(K_{UUU}+K_{UVV}-G_{UUV}-G_{VVV}\right)\right)|}_{\left(0,0\right)}\\ =-\left(0.014112+0.102564\alpha \right)-i\left(0.016+0.116297\alpha \right)\end{array}$.

由不动点的局部分支理论 [7] 可知， $\alpha =0$ 时系统(3)的不动点(0, 0)发生了Neimark-Sacker分支。当 $\alpha >0$ ( $\left|\alpha \right|$ 充分小)时，不动点(0, 0)失去稳定性，并在(0, 0)的小邻域内生成一族稳定的周期轨。因为系统(3)的不动点(0, 0) ( $\alpha =0$ 时)与系统(1)的不动点 $Z_0=\left(0,0.3\right)$ ( $\delta =0.25$ 时)的局部拓扑结构是等价的，所以当 $\delta =0.25$ 时， $Z_0$ 发生了Neimark-Sacker分支，命题得证。

2.2. Neimark-Sacker分支的控制

在系统(1)中加入线性的状态反馈控制器 $u\left(x,y\right)=A_{11}x+A_{12}\left(y-0.3\right)$，得到了系统(4)，

$\left(\begin{array}{c}x\\ y\end{array}\right)\to \left(\begin{array}{c}x+\delta \left(x-\frac{x^3}{3}-y+0.3\right)+A_{11}x+A_{12}\left(y-0.3\right)\\ y+1.25\delta \left(1.8x+0.3-y\right)\end{array}\right)$ (4)

其中 $A_{11}$ 、 $A_{12}$ 为控制参数， $Z_0=\left(0,0.3\right)$ 仍为系统(4)的不动点， ${\delta }_0=0.25$ 为未控制系统(1)的不动点 $Z_0$ 发生Neimark-Sacker分支的分支值，下面考虑控制系统(4)中该不动点Neimark-Sacker分支的存在性。

引理：设 $F\left(\delta \right)={\delta }^2-\left(0.25+1.25A_{11}+2.25A_{12}\right)\delta +A_{11}$，判别式 $\Delta =1.5625A_{11}^2+5.625A_{11}{A}_{12}+5.0625A_{12}^2+1.125A_{12}-3.375A_{11}+0.0625$，

(i) 当 $A_{11}>0$， $\frac{11A_{11}}{9}<A_{12}$， $\frac{3-A_{11}}{9}\le A_{12}$ 时， $F\left(\delta \right)=0$ 在区间(0, 0.25)仅有一根 $\frac{0.25+1.25A_{11}+2.25A_{12}-\sqrt{\Delta }}{2}$ ；

(ii) 当 $A_{11}<0$， $\frac{11A_{11}}{9}>A_{12}$ 时， $F\left(\delta \right)=0$ 在区间(0, 0.25)仅有一根 $\frac{0.25+1.25A_{11}+2.25A_{12}+\sqrt{\Delta }}{2}$ ；

(iii) 当 $A_{11}>0$， $\frac{-1-5A_{11}}{9}<A_{12}<\min \left\{\frac{1-5A_{11}}{9},\frac{11A_{11}}{9}\right\}$， $\Delta >0$ 时， $F\left(\delta \right)=0$ 在区间(0, 0.25)有两根 $\frac{0.25+1.25A_{11}+2.25A_{12}\pm \sqrt{\Delta }}{2}$ ；

(iv) 当 $A_{11}=0$， $-\frac{1}{9}<A_{12}<0$ 时， $F\left(\delta \right)=0$ 在区间(0, 0.25)仅有一根 $\frac{\sqrt{5.0625A_{12}^2+1.125A_{12}+0.0625}+0.25}{2}+\frac{2.25A_{12}}{2}$ ；

(v) 当 $0<A_{11}<\frac{1}{6}$， $\frac{11A_{11}}{9}=A_{12}$ 时， $F\left(\delta \right)=0$ 在区间(0, 0.25)仅有一根 $\frac{-\sqrt{16A_{11}^2-2A_{11}+0.0625}+0.25}{2}+\frac{3.875A_{11}}{2}$ ；

(I) 当 $0.25<A_{11}$， $\frac{3-A_{11}}{9}<A_{12}<\frac{11A_{11}}{9}$ 时， $F\left(\delta \right)=0$ 在区间(0.25, 1)仅有一根 $\frac{0.25+1.25A_{11}+2.25A_{12}-\sqrt{\Delta }}{2}$ ；

(II) 当 $A_{11}\le 0$， $\frac{11A_{11}}{9}<A_{12}<\frac{3-A_{11}}{9}$ 时， $F\left(\delta \right)=0$ 在区间(0.25, 1)仅有一根 $\frac{0.25+1.25A_{11}+2.25A_{12}+\sqrt{\Delta }}{2}$ ；

(III) 当 $\frac{1}{16}\le A_{11}$， $\frac{1-5A_{11}}{9}<A_{12}<\min \left\{\frac{7-5A_{11}}{9},\frac{11A_{11}}{9},\frac{3-A_{11}}{9}\right\}$， $\Delta >0$ 时， $F\left(\delta \right)=0$ 在区间(0.25, 1)有两根 $\frac{0.25+1.25A_{11}+2.25A_{12}\pm \sqrt{\Delta }}{2}$ ；

(IV) 当 $0<A_{11}<\frac{1}{16}$， $\frac{11A_{11}}{9}=A_{12}$ 时， $F\left(\delta \right)=0$ 在区间(0.25, 1)仅有一根 $\frac{\sqrt{16A_{11}^2-2A_{11}+0.0625}+0.25}{2}+\frac{3.875A_{11}}{2}$ ；

(V) 当 $0.25<A_{11}<1$， $A_{12}=\frac{3-A_{11}}{9}$ 时， $F\left(\delta \right)=0$ 在区间(0.25, 1)仅有一根 $\frac{1+0.875A_{11}-\sqrt{A_{11}^2-2A_{11}+1}}{2}$。

证明： $F\left(0\right)=A_{11}$， $F\left(0.25\right)=\frac{9}{16}\left(\frac{11A_{11}}{9}-A_{12}\right)$， $F\left(1\right)=\frac{9}{4}\left(\frac{3-A_{11}}{9}-A_{12}\right)$， $F\left(\delta \right)$ 的对称轴为 $\frac{1+5A_{11}+9A_{12}}{8}$。

(i) 显然 $F\left(0\right)>0$， $F\left(0.25\right)<0$，由根的存在性定理得， $F\left(\delta \right)=0$ 在区间(0, 0.25)仅有一根 $\frac{0.25+1.25A_{11}}{2}+\frac{2.25A_{12}-\sqrt{\Delta }}{2}$ ；

(ii) 易知 $F\left(0\right)<0$， $F\left(0.25\right)>0$，从而 $F\left(\delta \right)=0$ 在区间(0, 0.25)有一根 $\frac{0.25+1.25A_{11}+2.25A_{12}+\sqrt{\Delta }}{2}$ ；

(iii) 显然 $F\left(0\right)>0$， $F\left(0.25\right)>0$，由 $\frac{-1-5A_{11}}{9}<A_{12}<\frac{1-5A_{11}}{9}$ 可得 $F\left(\delta \right)$ 的对称轴 $\frac{1+5A_{11}+9A_{11}}{8}\in \left(0,0.25\right)$。

又因判别式 $\Delta >0$，故 $F\left(\delta \right)=0$ 在(0, 0.25)有两根 $\frac{0.25+1.25A_{11}+2.25A_{12}\pm \sqrt{\Delta }}{2}$ ；

(iv) 由已知可得 $F\left(0\right)=0$， $F\left(0.25\right)=-\frac{9A_{12}}{16}>0$， $F\left(\delta \right)$ 的对称轴 $\frac{1+9A_{12}}{8}>0$，从而 $F\left(\delta \right)=0$ 在(0, 0.25)中存在一根 $\frac{0.25+2.25A_{12}+\sqrt{5.0625A_{12}^2+1.125A_{12}+0.0625}}{2}$ ；

(v) 由已知可得 $F\left(\delta \right)$ 的对称轴 $\frac{1+5A_{11}+9A_{12}}{8}=\frac{1+16A_{11}}{8}<0.25$， $F\left(0\right)>0$， $F\left(0.25\right)=0$，从而可得 $F\left(\delta \right)=0$ 在(0,0.25)中存在一根 $\frac{0.25+3.875A_{11}-\sqrt{16A_{11}^2-2A_{11}+0.0625}}{2}$。

同理可证(I)~(V)。

定理2：若控制参数 $A_{11}$ 和 $A_{12}$ 满足引理条件之一，且

$\left(-0.421875A_{11}+0.140625A_{12}-0.984375\right){\delta }^{*}+A_{11}^2+3.9375A_{11}<0$ (5)

${\delta }^{*}\ne 0.125+0.625A_{11}+1.125A_{12}$ (6)

${\delta }^{*}\ne A_{12}$ (7)

$1+{\delta }^{*}+A_{11}\ne 0$ (8)

这里 ${\delta }^{*}={\delta }^{*}\left(A_{11},A_{12}\right)=\frac{0.25+1.25A_{11}+2.25A_{12}-\sqrt{\Delta }}{2}$ 或 ${\delta }^{*}={\delta }^{*}\left(A_{11},A_{12}\right)=\frac{0.25+1.25A_{11}+2.25A_{12}+\sqrt{\Delta }}{2}$，则

当 $\delta ={\delta }^{*}$ 时，控制系统(4)的不动点 $Z_0=\left(0,0.3\right)$ 发生了Neimark-Sacker分支。

证明：令 $u_1=x$， $v_1=y-0.3$， $\beta =\delta -{\delta }^{*}$，则由系统(4)得

$\left(\begin{array}{l}{u}_1\\ v_1\end{array}\right)\to \left(\begin{array}{cc}1+{\delta }^{*}+A_{11}& -{\delta }^{*}+A_{12}\\ 2.25{\delta }^{*}& 1-1.25{\delta }^{*}\end{array}\right)\left(\begin{array}{l}{u}_1\\ v_1\end{array}\right)+\left(\begin{array}{c}-\frac{{\delta }^{*}}{3}{u}_1^3+\beta \left(u_1-\frac{u_1^3}{3}-v_1\right)\\ \beta \left(2.25u_1-1.25v_1\right)\end{array}\right)$ (9)

系统(9)在不动点(0, 0)处的Jocobian矩阵为

$J=\left(\begin{array}{cc}1+{\delta }^{*}+A_{11}+\beta & -{\delta }^{*}+A_{12}-\beta \\ 2.25\left({\delta }^{*}+\beta \right)& 1-1.25\left({\delta }^{*}+\beta \right)\end{array}\right)$

其特征方程为 ${\lambda }^2+p\left(\beta \right)\lambda +q\left(\beta \right)=0$，其中 $p\left(\beta \right)=-2+0.25\left({\delta }^{*}+\beta \right)-A_{11}$， $q\left(\beta \right)={\beta }^2+\left(2{\delta }^{*}-\left(0.25+1.25A_{11}+2.25A_{12}\right)\right)\beta +1-0.25{\delta }^{*}+{\left({\delta }^{*}\right)}^2+\left(1-1.25{\delta }^{*}\right)A_{11}-2.25{\delta }^{*}{A}_{12}$。当 $\beta =0$ 时，由引理可得 $q\left(0\right)-1={\left({\delta }^{*}\right)}^2-\left(0.25+1.25A_{11}+2.25A_{12}\right){\delta }^{*}+A_{11}=0$，

$\begin{array}{c}{p}^2\left(0\right)-4q\left(0\right)=-3.9375{\left({\delta }^{*}\right)}^2+\left(4.5A_{11}+9A_{12}\right){\delta }^{*}+A_{11}^2\\ =-3.9375\left(\left(0.25+1.25A_{11}+2.25A_{12}\right){\delta }^{*}-A_{11}\right)+\left(4.5A_{11}+9A_{12}\right){\delta }^{*}+A_{11}^2\\ =\left(-0.421875A_{11}+0.140625A_{12}-0.984375\right){\delta }^{*}+A_{11}^2+3.9375A_{11},\end{array}$

又由(5)可知， $p^2\left(0\right)-4q\left(0\right)<0$，故 $\beta =0$ 时，(0, 0)的特征值为一对模为1的共轭复数 ${\lambda }_{1，2}\left(0\right)=\frac{-p\left(0\right)}{2}\pm i\frac{\sqrt{4-p^2\left(0\right)}}{2}$。

选取线性矩阵 $T_1=\left(\begin{array}{cc}2\left({\delta }^{*}-A_{12}\right)& 0\\ -2.25{\delta }^{*}-A_{11}& \sqrt{4-p^2\left(0\right)}\end{array}\right)$，系统(4)作变换 $\left(\begin{array}{l}{u}_1\\ v_1\end{array}\right)=T_1\left(\begin{array}{l}X\\ Y\end{array}\right)$ 得

$\left(\begin{array}{l}X\\ Y\end{array}\right)\to \left(\begin{array}{cc}-\frac{p\left(0\right)}{2}& \frac{\sqrt{4-p^2\left(0\right)}}{2}\\ -\frac{\sqrt{4-p^2\left(0\right)}}{2}& -\frac{p\left(0\right)}{2}\end{array}\right)\left(\begin{array}{l}X\\ Y\end{array}\right)+\left(\begin{array}{l}g\left(X,Y\right)\\ h\left(X,Y\right)\end{array}\right)$ (10)

$g\left(X,Y\right)=-\frac{4{\delta }^{*}{\left({\delta }^{*}-A_{12}\right)}^2}{3}{X}^3+\frac{\beta }{2\left({\delta }^{*}-A_{12}\right)}\left(\left(4.25{\delta }^{*}+A_{11}-2A_{12}\right)X-\frac{8{\left({\delta }^{*}-A_{12}\right)}^3}{3}{X}^3-\sqrt{4-p^2\left(0\right)}Y\right)$,

$\begin{array}{c}h\left(X,Y\right)=-\frac{4{\delta }^{*}\left(2.25{\delta }^{*}+A_{11}\right){\left({\delta }^{*}-A_{12}\right)}^2}{3\sqrt{4-p^2\left(0\right)}}{X}^3+\frac{\beta }{\sqrt{4-p^2\left(0\right)}}(\frac{1}{2\left({\delta }^{*}-A_{12}\right)}(25.1875{\left({\delta }^{*}\right)}^2\\ {}^{{}_{}{}^{}}+\left(4A_{11}-24.625A_{12}\right){\delta }^{*}+A_{11}^2+0.5A_{11}{A}_{12}+A_{12}^2)X\\ -\frac{4\left(2.25{\delta }^{*}+A_{11}\right){\left({\delta }^{*}-A_{12}\right)}^2}{3}{X}^3+\left(3.5{\delta }^{*}-0.25A_{12}\right)Y).\end{array}$

由(6)得 $d^{*}={\frac{\text{d}\left|\lambda \left(\beta \right)\right|}{\text{d}\delta }|}_{\beta =0}={\frac{\text{d}\sqrt{q\left(\beta \right)}}{\text{d}\delta }|}_{\beta =0}={\delta }^{*}-0.125-0.625A_{11}-1.125A_{12}\ne 0$。

$P_{20}=\frac{1}{8}{\left(g_{XX}-g_{YY}+2h_{XY}+i\left(h_{XX}-h_{YY}-2g_{XY}\right)\right)|}_{\left(0,0\right)}=0$,

$P_{11}=\frac{1}{4}{\left(g_{XX}+g_{YY}+i\left(h_{XX}+h_{YY}\right)\right)|}_{\left(0,0\right)}=0$,

$P_{02}=\frac{1}{8}{\left(g_{XX}-g_{YY}-2h_{XY}+i\left(h_{XX}-h_{YY}+2g_{XY}\right)\right)|}_{\left(0,0\right)}=0$,

$\begin{array}{c}{P}_{21}=\frac{1}{16}{\left(\left(g_{XXX}+g_{XYY}+h_{XXY}+h_{YYY}\right)+i\left(h_{XXX}+h_{XYY}-g_{XXY}-g_{YYY}\right)\right)|}_{\left(0,0\right)}\\ =-\frac{{\delta }^{*}{\left({\delta }^{*}-A_{12}\right)}^2}{2}\left(1+\frac{2.25{\delta }^{*}+A_{11}}{\sqrt{4-p^2\left(0\right)}}i\right).\end{array}$

由(7) (8)知 $l_1=-\mathrm{Re}\left[\frac{\left(1-2\lambda \right){\bar{\lambda }}^2}{1-\lambda }{P}_{11}{P}_{20}\right]-\frac{1}{2}{\left|P_{11}\right|}^2-{\left|P_{02}\right|}^2+\mathrm{Re}\left(\bar{\lambda }{P}_{21}\right)=-\frac{{\delta }^{*}{\left({\delta }^{*}-A_{12}\right)}^2}{2}\left(1+{\delta }^{*}+A_{11}\right)\ne 0$，从而

当 $\beta =0$ 时，系统(10)的不动点(0, 0)发生了Neimark-Sacker分支。因此当 $\delta ={\delta }^{*}$ 时，控制系统(4)的不动点 $Z_1=\left(0,0.3\right)$ 发生了Neimark-Sacker分支，故定理成立。

由引理以及定理2可知，控制参数 $A_{11}$ 和 $A_{12}$ 可以调节控制系统(4)不动点 $Z_0$ 发生Neimark-Sacker分支的分支值，从而可使 $Z_1=\left(0,0.3\right)$ 的Neimark-Sacker分支的发生提前或者延迟。

3. 数值模拟

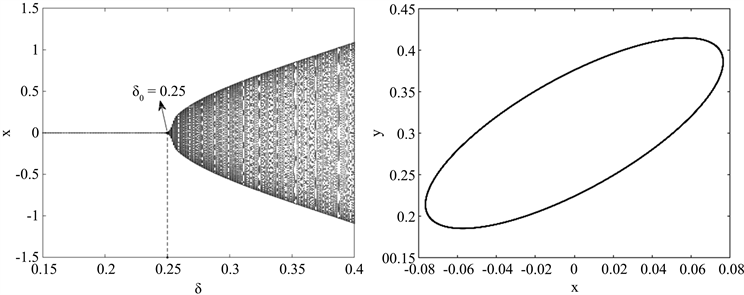
图1(a)为系统(1)不动点 $Z_0$ 在 $\left(\delta ,x\right)$ 平面的分支图，图中展示了神经元膜电位随 $\delta$ 改变发生的动态变化。当 $\delta =0.25$ 时，系统(1)的不动点 $Z_0$ 发生了Neimark-Sacker分支；当 $\delta >0.25$ 时，不动点 $Z_0$ 失去稳定性，并在 $Z_0$ 的小邻域内有一族稳定的周期轨生成。图1(b)展示了当 $\delta =0.251$ 时系统(1)周期轨的相图。

(a)(b)

Figure 1. (a) Bigurcation diagram of the fixed point $Z_0$ of the system (1) for $\delta \in \left(0.15,0.4\right)$ ; (b) Phase diagram of the periodic orbit for $\delta =0.251$

图1. (a) $\delta \in \left(0.15,0.4\right)$ 时原系统(1)不动点 $Z_0$ 分支图；(b) $\delta =0.251$ 时周期轨的相图

下面考虑控制器对不动点 $Z_0$ 的Neimark-Sacker分支的控制。

1) Neimark-Sacker分支的提前：取 $A_{11}=0$， $A_{11}=-\frac{1}{45}$， $A_{11}$ 和 $A_{12}$ 满足引理(iv)条件： $A_{11}=0$， $-\frac{1}{9}<-\frac{1}{45}=A_{12}<0$。从而 ${\delta }^{*}=0.2$，因为 $A_{11}$ 和 $A_{12}$ 还满足定理2的条件：

$\left(-0.421875A_{11}+0.140625A_{12}-0.984375\right){\delta }^{*}+A_{11}^2+3.9375A_{11}=-0.1975<0$， $0.125+0.625A_{11}+1.125A_{12}=0.1\ne {\delta }^{*}$， $0.2={\delta }^{*}\ne A_{12}$， $1+{\delta }^{*}+A_{11}=1.2\ne 0$。所以当 $\delta =0.2$ 时，控制系统(4)的不动点 $Z_0$ 发生了Neimark-Sacker分支，即Neimark-Sacker分支提前发生。 $\delta \in \left(0.15,0.4\right)$ 时 $\left(\delta ,x\right)$ 平面上控制系统(4)不动点 $Z_0$ 的分支图如图2所示。

2) Neimark-Sacker分支的延迟：令 $A_{11}=-1$， $A_{11}=-\frac{2}{9}$， $A_{11}$ 和 $A_{12}$ 满足引理(II)条件： $A_{11}<0$， $\frac{11A_{11}}{9}=-\frac{11}{9}<A_{12}<\frac{4}{9}=\frac{3-A_{11}}{9}$。从而 ${\delta }^{*}=0.5$，又由于 $A_{11}$ 和 $A_{12}$ 满足定理2条件：

$\left(-0.421875A_{11}+0.140625A_{12}-0.984375\right){\delta }^{*}+A_{11}^2+3.9375A_{11}=-3.234375<0$， $0.125+0.625A_{11}+1.125A_{12}=-0.75\ne {\delta }^{*}$， $0.5={\delta }^{*}\ne A_{12}$， $1+{\delta }^{*}+A_{11}=0.5\ne 0$。故当 $\delta =0.5$ 时，控制系统(4)的不动点 $Z_0$ 发生了Neimark-Sacker分支，即Neimark-Sacker分支延迟发生，此时控制系统(4)不动点 $Z_0$ 分支图如图3所示。

Figure 2. Bigurcation diagram of the fixed point $Z_0$ of the system (4) for $A_{11}=0$, $A_{11}=-\frac{1}{45}$

图2. $A_{11}=0$， $A_{11}=-\frac{1}{45}$ 时，控制系统(4)的不动点 $Z_0$ 分支图

Figure 3. Bigurcation diagram of the fixed point $Z_0$ of the system (4) for $A_{11}=-1$, $A_{11}=-\frac{2}{9}$

图3. $A_{11}=-1$， $A_{11}=-\frac{2}{9}$ 时，控制系统(4)的不动点 $Z_0$ 分支图

由前面的理论分析，我们对控制参数 $A_{11}$ 和 $A_{12}$ 满足的分支控制效应进行了区域划分，如图4所示。

当 $A_{11}$ 、 $A_{12}$ 属于区域(i)~(v)时，不动点 $Z_0$ 提前发生Neimark-Sacker分支；当 $A_{11}$ 、 $A_{12}$ 属于区域(I)~(V)时，不动点 $Z_0$ 延迟发生Neimark-Sacker分支。

Figure 4. Effective domain of the control parameters A₁₁ and A₁₂

图4. 控制参数A₁₁与A₁₂的效应域

4. 结论

本文研究了离散FHN系统不动点的Neimark-Sacker分支控制问题，我们设计了一个简单的状态反馈控制器，通过严格的理论分析可知，Neimark-Sacker分支的分支值由控制参数 $A_{11}$ 和 $A_{12}$ 决定，结合数值计算表明该控制器中的控制参数 $A_{11}$ 和 $A_{12}$ 可以精准地控制Neimark-Sacker分支的分支值增大或者减小，从而控制不动点提前或延迟发生Neimark-Sacker分支。

致谢

诚挚地感谢我的恩师，老师教会我学习要求真务实，脚踏实地，做事要注重高效率，精益求精。本文的成型离不开老师的耐心指导和修改，在此我要向导师表达深深的敬意与祝福。

此外感谢其他老师同学朋友给予的帮助，最后感谢审稿老师给出的宝贵意见和建议。