各向异性张量加权分数阶变分图像去噪模型

Anisotropic Tensor Weighted Fractional-Order Variation Image Denoising Model

摘要: 为了增强去噪后图像的边缘和保留图像纹理，本文提出了一种新的各向异性张量加权分数阶变分图像去噪模型，即利用分数阶的Jacobian矩阵形式与一个各向异性张量的乘积的Frobenius范数，作为本文模型的正则化子，其包含图像在每个像素点的局部邻域变化的信息，根据图像结构灵活地控制和定向去除噪声，增强图像的边缘和保留纹理细节信息。本文采用交替方向乘子(ADMM)法进行数值求解，所有的子问题都具有闭形解。数值实验表明，该模型复原的图像有效地保留图像的边缘和纹理等细节特征，抑制阶梯效应，与其他模型相比更具有竞争力。

Abstract: In order to enhance the edge of the denoised image and preserve the texture of the image, a new anisotropic tensor weighted Fractional-order Variation image denoising model is proposed in this paper, which uses the Frobenius norm of the product of fractional Jacobian matrix form and an anisotropic tensor as the regularizer of this model. It contains the local neighborhood change information of the image at each pixel point, and can flexibly control and directionally remove noise and enhance edge according to the image structure, and retain texture details. In this paper, alternate directional multipliers method (ADMM) is used to solve numerical problems. Numerical experiments show that this model can effectively retain the edge and texture of the image and suppress the step effect, which is more competitive than other models.

1. 引言

图像去噪在医学成像、卫星成像及模式识别等领域中具有重要意义。在图像去噪的开创性工作中，Perona和Malik [1] 提出了一种非线性扩散的偏微分方程用于图像去噪，复原的图像有效保留图像的线条和结构，但沿图像的线条和边缘保留了噪声。于是Weickert [2] 提出一种基于张量的图像扩散方程，基于张量扩散的原理：对平行于图像结构的区域进行平滑处理，利用一个张量场来描述局部方向，使图像平滑并与图像结构平行，利用非线性扩散函数对张量场进行变换，将变换后的张量场用于扩散方程，得到的张量为扩散张量。扩散张量包含了图像在每个点的局部邻域变化的信息，可以根据图像结构更灵活地控制和定向去除图像结构的线条和边缘处噪声，因此，受到学者的广泛认可。

由于沿张量的两个特征向量的方向，具有不同的传导系数，故张量扩散也被称为“各向异性张量扩散”。在图像处理的应用中受到广泛关注。2010年，Grasmair和Lenzen [3] [4] 提出各向异性全变分模型，将扩散方程与变分法相结合，用一个各向异性项来替代各向同性TV半范数作为模型的正则化子，复原的图像在抑制块伪影产生的同时降低阶梯效应。2013年，Roussous和Maragos [5] 提出由张量全变分和Beltrami泛函的推广导出了基于张量的图像扩散，基于结构张量来描述每个点的邻域内图像结构的几何形状，通过在包含图像块的高维空间中用嵌入表示图像来推广Beltrami函数，该模型中的扩散能有效地控制扩散方向，从而保留图像的边缘和结构。2015年，Freddie等 [6] [7] 人提出了一种基于张量的变分公式用于彩色图像去噪，引入了一个基于张量的函数—梯度能量全变分，作为新的正则化子，其复原的图像具有更清晰的边缘。然而，上述已有的基于变分法和各向异性扩散相结合的模型仅考虑了全变分 [8] [9] [10] 模型。但是全变分模型倾向于分段常数解，在平滑区域存在阶梯效应，且不能有效复原图像纹理细节信息。2007年，Bai J等 [11] 提出分数阶去噪模型，该模型通过定义图像强度函数的分数阶导数绝对值的递增函数为损失函数，再采用折叠算法来消除跨越边界的跳跃不连续，有效保留图像的纹理细节信息，抑制阶梯效应。

基于此，本文提出了一种各向异性张量加权分数阶变分模型(Tensor Weighted Fractional-order Variation, TWFO)，利用分数阶的Jacobian矩阵形式和一个各向异性张量的乘积的Frobenius范数，提出了一种新的正则化子，使分数阶变分成为一个有效集成方向信息的非线性各向异性分数阶模型。我们利用高斯核来定义输入图像的每一个像素点的结构张量，求出其特征向量，再根据图像去噪的要求，利用文献 [14] 的特征值构造本文新的各向异性张量。通过大量的数值实验，我们发现TWFO模型可以根据图像的结构灵活的控制扩散的方向和去除图像中的噪声，抑制阶梯效应，增强去噪图像中物体的边缘，保留图像纹理细节信息。所提出的模型是基于变分框架的，因此ADMM可以有效地求解该模型。

2. 相关背景

2.1. 分数阶 [12] [13] 的定义

本文考虑分数阶变分作为图像先验。给定一个图像域 $\Omega \subset {ℝ}^2$，将其离散为一个矩形网格 $\left\{\left(x_i,y_i\right):1\le i\le m,1\le j\le n\right\}$。然后图像可以表示为欧几里得空间 $\Omega \subset {ℝ}^{m\times n}$ 中的矩阵，记为 $u_{i,j}=u\left(x_i,y_i\right)$。对于特定阶 $\alpha >0$ 的导数，其中 $\alpha$ 可以是一个分数， $\alpha$ 阶变分函数 $u:\Omega \to ℝ$ 通过引入分数阶导数扩展了传统的TV模型。特别地，基于Grünwald-Letnikov分数阶导数 [14]，将离散分数阶梯度定义为：

${\nabla }^{\alpha }u={\left[D_1^{\alpha }u,D_2^{\alpha }u\right]}^{{\rm T}}$

其中，分数阶导数 $D_1^{\alpha }u,D_2^{\alpha }u\in {ℝ}^{m\times n}$ 分别为沿 $x,y$ 方向的分数阶导数，则有

$\begin{array}{l}{\left(D_1^{\alpha }u\right)}_{i,j}={\displaystyle \underset{k=0}{\overset{K-1}{\sum }}{\left(-1\right)}^k{C}_k^{\alpha }{u}_{i-k,j}},\\ {\left(D_2^{\alpha }u\right)}_{i,j}={\displaystyle \underset{k=0}{\overset{K-1}{\sum }}{\left(-1\right)}^k{C}_k^{\alpha }{u}_{i,j-k}},\end{array}$

这里K是用来近似分数阶导数每个像素的相邻像素的个数。定义系数 ${\left\{C_k^{\alpha }\right\}}_{k=0}^{K-1}$ 用Gamma函数 $\Gamma \left(x\right)$ 定义为 $C_k^{\alpha }=\frac{\Gamma \left(\alpha +1\right)}{\Gamma \left(k+1\right)\Gamma \left(\alpha +1-k\right)}$，然后定义u的离散分数阶变分为：

${\Vert {\nabla }^{\alpha }u\Vert }_1={\displaystyle \underset{i,j}{\sum }\left(\left|{\left(D_1^{\alpha }u\right)}_{i,j}\right|+\left|{\left(D_2^{\alpha }u\right)}_{i,j}\right|\right)}$,

根据 ${\left({\nabla }^{\alpha }\right)}^{\ast }=\overline{{\left(-1\right)}^{\alpha }}di{v}^{\alpha }$ 的关系，给出了 $p=\left(p^{\left(1\right)},p^{\left(2\right)}\right)\in {ℝ}^{m\times n}\times {ℝ}^{m\times n}$ 的离散分数阶散度：

${\left(di{v}^{\alpha }p\right)}_{i,j}={\left(-1\right)}^{\alpha }{\displaystyle \underset{k=0}{\overset{K-1}{\sum }}{\left(-1\right)}^k{C}_k^{\alpha }\left(p_{i+k,j}^{\left(1\right)}+p_{i,j+k}^{\left(2\right)}\right)}$。

2.2. 张量扩散 [2]

在图像处理中常用 $2\times 2$ 对称矩阵 $D=\left(\begin{array}{cc}a& b\\ b& c\end{array}\right)$ 作为扩散张量，则有张量扩散方程： $\frac{\partial u}{\partial t}=div\left(D\nabla u\right)$。

在正交系 $\left(x,y\right)$ 中：

$\frac{\partial u}{\partial t}=div\left(D\nabla u\right)=\frac{\partial }{\partial x}\left(a{u}_x+b{u}_y\right)+\frac{\partial }{\partial y}\left(b{u}_x+c{u}_y\right)$,

可得，在固定坐标系 $\left(x,y\right)$ 中，张量扩散方程不能表示为两个一维扩散之和，但利用矩阵D的两个特征向量 $\left(v_1,v_2\right)$ 构成局部坐标系，设D的两个特征值为 ${\lambda }_1,{\lambda }_2$，再由矩阵的本征分解定理，则有

$D={\lambda }_1{v}_1{v}_1^{{\rm T}}+{\lambda }_2{v}_2{v}_2^{{\rm T}}$,

由 $\nabla u=\frac{\partial u}{\partial v_1}{v}_1+\frac{\partial u}{\partial v_2}{v}_2$，再考虑到特征向量 $\left(v_1,v_2\right)$ 的正交归一化性，可得

$div\left(D\nabla u\right)=\frac{\partial }{\partial v_1}\left({\mu }_1\frac{\partial u}{\partial v_1}\right)+\frac{\partial }{\partial v_2}\left({\mu }_2\frac{\partial u}{\partial v_2}\right)$,

上式表明，在特定的局部坐标系 $\left(v_1,v_2\right)$ 中，张量扩散也可以表达为沿 $v_1$ 和 $v_2$ 两个相互正交方向的一维扩散之和，但沿这两个方向，具有不同的传导系数，故张量扩散也被称为“各向异性张量扩散”。

2.3. 张量的特征值和特征向量的意义

我们可知P-M方程的扩散行为只受图像的梯度的模值所控制，然而，图像的局部结构信息并不仅仅表现为图像的梯度。为了获取更丰富的局部结构信息，本文利用如下定义的散布矩阵 $J_{\rho }$ ：

$J_{\rho }=\left(\begin{array}{cc}{j}_{11}& j_{12}\\ j_{12}& j_{22}\end{array}\right)=\left(\begin{array}{cc}{\left(\frac{\partial I_{\sigma }}{\partial x}\right)}^2\ast G_{\rho }& \left(\frac{\partial I_{\sigma }}{\partial x}\frac{\partial I_{\sigma }}{\partial y}\right)\ast G_{\rho }\\ \left(\frac{\partial I_{\sigma }}{\partial x}\frac{\partial I_{\sigma }}{\partial y}\right)\ast G_{\rho }& {\left(\frac{\partial I_{\sigma }}{\partial y}\right)}^2\ast G_{\rho }\end{array}\right)$ (1)

式中 $I_{\sigma }$ 表示以参数 $\sigma$ 的平滑图像， $G_{\rho }$ 表示以 $\rho$ 为参数的Gaussian核。 $J_{\rho }$ 表示输入图像的结构张量，为实对称矩阵，两个特征值 ${\lambda }_1$， ${\lambda }_2$ 解得：

${\lambda }_{1,2}=\frac{1}{2}\left(j_{11}+j_{22}\pm \sqrt{{\left(j_{11}-j_{22}\right)}^2+4j_{12}^2}\right)$,

约定 ${\lambda }_1$ 对应于上式中的正号， ${\lambda }_2$ 取负号，即 ${\lambda }_1>{\lambda }_2$。它们对应的特征向量分别为 $v_1$ 和 $v_2$，有 $v_i=\left(\cos {\theta }_i,\sin {\theta }_i\right),i=1,2$。

一个二维函数与二维Gaussian核的卷积相当于在其每一点的一个尺度为 $\rho$ 的邻域取加权平均。所以散布矩阵的特征值 ${\lambda }_1$ 所表示的是，从尺度为 $\rho$ 的邻域平均来看，灰度变化最快的取向为 $v_1$，其变化率为 $\sqrt{{\lambda }_1}$。而在同一点的同一邻域内，变化最慢的取向为 $v_2$，其变化率为 $\sqrt{{\lambda }_2}$。以下分三种情况来讨论图像的局部特征：

1) ${\lambda }_1\approx {\lambda }_2\approx 0$

这表示图像在该点附近沿任何方向灰度变化都很小，即为图像平坦区。

2) ${\lambda }_1\gg {\lambda }_2\approx 0$

这时图像沿某一方向的变化率远大于沿垂直于此方向的变化率。这是图像具有明显边缘或流线状结构的表现。在这一局部的灰度值表现出很强的相干性，可用图像局部相干性的量度： $H:={\left({\lambda }_1-{\lambda }_2\right)}^2={\left(j_{11}-j_{22}\right)}^2+4j_{12}^2$，显然，在(1)表示的平坦区，相干性 $H=0$。

3) ${\lambda }_1\approx {\lambda }_2\gg 0$

这表示图像在两个相互垂直的方向上，灰度都有相当快的变化，相干性也很小 $H\approx 0$。

3. 本文模型与算法

3.1. 模型的提出

1) TWFO模型

本文利用分数阶的Jacobian矩阵形式和一个各向异性张量的乘积的Frobenius范数，提出一种各向异性张量加权分数阶变分图像复原模型：

$\underset{u}{\min }\left\{\frac{\eta }{2}{\Vert u-f\Vert }_2^2+{\Vert T{\nabla }^{\alpha }u\Vert }_1\right\}$ (2)

其中，第一项 $\frac{\eta }{2}{\Vert u-f\Vert }_2$ 是数据保真项，用于度量待求图像u和观测图像f的接近程度，第二项 ${\Vert T{\nabla }^{\alpha }u\Vert }_1$ 是

正则项，用于提供图像u的先验知识， ${\nabla }^{\alpha }$ 为分数阶梯度算子，表示为Jacobian矩阵的形式： ${\left(\begin{array}{cc}{\partial }_x^{\alpha }& {\partial }_y^{\alpha }\end{array}\right)}^{{\rm T}}$， $\alpha$ 为分数阶的阶数， $1\le \alpha \le 2$ ； $\eta$ 是正则化参数，且 $0\le \eta \le 1$。

在正则项 ${\Vert T{\nabla }^{\alpha }u\Vert }_1$ 中， $T$ 为 $2\times 2$ 的对称半正定的扩散张量。它的四个分量是 $T_{11},T_{12},T_{21},T_{22}$。它们是由输入观测图像f计算出来的。正则项 ${\Vert T{\nabla }^{\alpha }u\Vert }_1$ 是 $2\times 2$ 张量 $T$ 乘以 $2\times 1$ Jacobian矩阵 ${\nabla }^{\alpha }$ 的Frobenius范数，其形式为：

$\left(\begin{array}{c}{T}_{11}{\partial }_x^{\alpha }u+T_{12}{\partial }_y^{\alpha }u\\ T_{21}{\partial }_x^{\alpha }u+T_{22}{\partial }_y^{\alpha }u\end{array}\right)$,

其中 $T$ 的两个正交特征向量张成旋转坐标系，在这个坐标系中计算输入图像的梯度。因此， $T$ 可以给有界Jacobian正则化子 ${\Vert {\nabla }^{\alpha }u\Vert }_1$ 引入方向，张量 $T$ 的特征值度量正则化子中的各向异性扩散的程度，并在两个方向上对由 [1] 中引入的结构张量的特征向量给出的 ${\nabla }^{\alpha }u$ 上的导数进行加权。

2) 模型解的存在性

现在，我们考虑TWFO模型解的存在性，首先，我们需要强制泛函的定义。

强制泛函的定义：设 $X$ 是线性赋范空间， $M\in X$， $f:M\to R$。若当 $x\in M$， $\Vert x\Vert \to \infty$ 时，有 $f\left(x\right)\to \infty$，

即 $\underset{\Vert x\Vert \to \infty }{\lim }f\left(x\right)=\infty$，则称f为强制的。特别地，当M为有界集时，总认为 $f:M\to R$ 是强制的。

定理：假设 $\eta >0$，模型(2)存在一个全局的极小值问题。

证明：为了便于求解，将模型(2)表示为

$\underset{u}{\min }{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\phi \left(u_{i,j}\right)}}=\frac{\eta }{2}{\Vert u_{i,j}-f_{i,j}\Vert }_2^2+\sqrt{A_{i,j}}$，

其中 $A_{i,j}={\left(T_{11}{\partial }_x^{\alpha }u+T_{12}{\partial }_y^{\alpha }u\right)}^2+{\left(T_{21}{\partial }_x^{\alpha }u+T_{22}{\partial }_y^{\alpha }u\right)}^2$，在上式中，我们只需要关注函数 $\phi \left(u_{i,j}\right)$，显然 $\phi \left(u_{i,j}\right)$ 是有界的，因为：

${\Vert u_{i,j}-f_{i,j}\Vert }_2\ge \left|{\Vert u_{i,j}\Vert }_2-{\Vert f_{i,j}\Vert }_2\right|$.

我们假设存在一个序列 $\left\{u_{i,j}^{\hat{k}}\right\}$，满足：

${\Vert u_{i,j}^{\hat{k}}-f_{i,j}\Vert }_2\to \infty$，当 ${\Vert u_{i,j}^{\hat{k}}\Vert }_2\to \infty$.

由强制泛函的定义可得， $\phi \left(u_{i,j}\right)$ 是强制泛函。现在，我们为 $\phi \left(u_{i,j}\right)$ 选取一个最小化序列 $\left\{u_{i,j}^l\right\}$，则 $\phi \left(u_{i,j}^l\right)$ 一定是有界的，又因为 $l^2$ 空间的有界序列验证了弱收敛子序列的存在性，即： $u_{i,j}^{l_s}\to u_{i,j}^{*}$。基于模型(2)的分段点意义上的可分性，则上述引理成立。证毕。

3.2. 图像局部结构张量信息提取

我们先求出输入图像u的结构张量 $J_{\rho }$ 的两个特征向量，由2.3节我们可知 $v_1=\left(\cos {\theta }_1,\sin {\theta }_1\right)$，

${\lambda }_1=\frac{1}{2}\left(j_{11}+j_{22}+\sqrt{{\left(j_{11}-j_{22}\right)}^2+4j_{12}^2}\right)$，则由 $\left|{\lambda }_{1}E-J_{\rho }\right|v_1^{{\rm T}}=0$ 求解 $v_1$，可解得 ${\theta }_1$ 和 ${\theta }_2$，分别为：

${\theta }_1=\frac{1}{2}\arctan \frac{2j_{12}}{j_{11}-j_{22}}$， ${\theta }_2={\theta }_1+\frac{\pi }{2}$。

则我们构造新的张量 $T$，由上述可知图像局部结构张量 $T$ 的特征向量与图像u结构张量 $J_{\rho }$ 的两个特征向量 $v_1$ 和 $v_2$ 平行，由于张量 $T$ 的特征值 ${\omega }_1$ 和 ${\omega }_2$ 根据不同的图像处理应用选择，则有

$T=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right)=\left(v_1,v_2\right)\left(\begin{array}{cc}{\omega }_1& 0\\ 0& {\omega }_2\end{array}\right)\left(\begin{array}{c}{v}_1^{{\rm T}}\\ v_2^{{\rm T}}\end{array}\right)$，

图像局部结构张量 $T$ 为实对称矩阵，本文研究的图像去噪问题目的是禁止图像边缘的扩散，并鼓励沿边缘的强扩散。因此，我们引用文献 [14] 中的两个特征值(扩散系数)：

${\omega }_1=\{\begin{array}{l}1s\le 0\\ 1-{\text{e}}^{\frac{-3.31488}{{\left(s/C\right)}^8}}s>0\end{array}$， ${\omega }_2=1$。

其中 $s=\left|\nabla u_{\sigma }\right|$ 为梯度幅值，C为对比参数。

3.3. 模型求解

直接求解TWFO模型是不能求解，因为：(1) TWFO模型是不光滑的；(2) 它耦合张量T和Jacobian矩阵 ${\nabla }^{\alpha }$ 在 ${\Vert T{\nabla }^{\alpha }u\Vert }_1$ 中，得到的欧拉—拉格朗日方程难以离散化计算求解。为了解决这两个难题，我们提出了一种基于ADMM [15] [16] [17] [18] 算法来最小化变分模型(2)。即利用本文模型的可分结构对模型进行分离变量求解，通过引入辅助变量 $V,W$，并将其转化为下述约束优化问题。

$\begin{array}{l}\underset{u,W,V}{\min }\left\{\frac{\eta }{2}{\Vert u-f\Vert }_2^2+{\Vert W\Vert }_1\right\}\\ \text{s}\text{.t}\text{.}V={\nabla }^{\alpha }u\\ W=TV\end{array}$ (3)

其中 $V=\left(V_1,V_2\right)$， $T=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right)$， $W=\left(W_1,W_1\right)$。然后构造增广拉格朗日函数，可将式(3)的最小化转化

为下面的鞍点问题。即

$\begin{array}{l}\underset{u,W,V}{\min }\underset{{\lambda }_1,{\lambda }_2}{\max }L\left(u,W,V,{\lambda }_1,{\lambda }_2\right)=\frac{\eta }{2}{\Vert u-f\Vert }_2^2+{\Vert W\Vert }_1+\langle {\lambda }_1^{{\rm T}},{\nabla }^{\alpha }u-V\rangle +\frac{{\mu }_1}{2}{\Vert {\nabla }^{\alpha }u-V\Vert }_2^2\\ +\langle {\lambda }_2^{{\rm T}},TV-W\rangle +\frac{{\mu }_2}{2}{\Vert TV-W\Vert }_2^2\end{array}$ (4)

合并同类项得：

$\underset{u,W,V}{\min }\underset{{\lambda }_1,{\lambda }_2}{\max }L\left(u,W,V,{\lambda }_1,{\lambda }_2\right)=\frac{\eta }{2}{\Vert u-f\Vert }_2^2+{\Vert W\Vert }_1+\frac{{\mu }_1}{2}{\Vert {\nabla }^{\alpha }u-V+\frac{{\lambda }_1^{{\rm T}}}{{\mu }_1}\Vert }_2^2+\frac{{\mu }_2}{2}{\Vert TV-W+\frac{{\lambda }_2^{{\rm T}}}{{\mu }_2}\Vert }_2^2$

其中： ${\lambda }_1,{\lambda }_2$ 为拉格朗日乘子， ${\mu }_1,{\mu }_2$ 为惩罚参数， $\langle ·,·\rangle$ 定义为内积，进一步：

$\{\begin{array}{l}{u}^{k+1}=\underset{u}{\mathrm{argmin}}\left\{\frac{\eta }{2}{\Vert u-f\Vert }_2^2+\frac{{\mu }_1}{2}{\Vert {\nabla }^{\alpha }u-V^k+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\Vert }_2^2\right\},\\ W^{k+1}=\underset{W}{\mathrm{argmin}}\left\{{\Vert W\Vert }_1+\frac{{\mu }_2}{2}{\Vert T{V}^k-W+\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2}\Vert }_2^2\right\},\\ V^{k+1}=\underset{V}{\mathrm{argmin}}\left\{\frac{{\mu }_1}{2}{\Vert {\nabla }^{\alpha }{u}^{k+1}-V+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\Vert }_2^2+\frac{{\mu }_2}{2}{\Vert TV-W^{k+1}+\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2}\Vert }_2^2\right\},\\ {\lambda }_1^{k+1}={\lambda }_1^k+{\mu }_1\left({\nabla }^{\alpha }{u}^{k+1}-V^{k+1}\right),\\ {\lambda }_2^{k+1}={\lambda }_2^k+{\mu }_2\left(T{V}^{k+1}-W^{k+1}\right).\end{array}$ (5)

下面求解各个子问题

1) 求解 $u$ -子问题，即求解下面方程

$u^{k+1}=\underset{u}{\mathrm{argmin}}\left\{\frac{\eta }{2}{\Vert u-f\Vert }_2^2+\frac{{\mu }_1}{2}{\Vert {\nabla }^{\alpha }u-V^k+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\Vert }_2^2\right\}$ (6)

该问题为光滑凸优化问题，对式子(6)关于u求偏导可得：

$\eta \left(u-f\right)+{\mu }_1{\left({\nabla }^{\alpha }\right)}^{\ast }\left({\nabla }^{\alpha }u-V^k+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\right)=0$ (7)

这里 ${\left({\nabla }^{\alpha }\right)}^{*}$ 是 ${\nabla }^{\alpha }$ 的伴随矩阵，在周期边界条件下，合并同类项，再对式子(7)利用快速傅里叶变换后，再利用快速傅里叶逆变换求解。

$u^{k+1}=F^{-1}\left(\frac{F\left(\eta f+{\mu }_1{\left({\nabla }^{\alpha }\right)}^{*}\left(V^k-\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\right)\right)}{F\left(\eta I+{\mu }_1{\left({\nabla }^{\alpha }\right)}^{*}{\nabla }^{\alpha }\right)}\right)$ (8)

其中 $F$ 和 $F^{-1}$ 分别表示傅里叶变换及其逆变换，此处的：矩阵除法、平方和绝对值都是按分量运算的。

2) 求解 $W$ -子问题，利用收缩算子给出 $W$ -子问题的闭形解，即求解下面这个极小值问题

$W^{k+1}=\underset{W}{\text{argmin}}\left\{{\Vert W\Vert }_1+\frac{{\mu }_2}{2}{\Vert T{V}^k-W+\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2}\Vert }_2^2\right\}$ (9)

满足收缩算法的条件,可得

$W^{k+1}=\mathrm{shrink}\left(T{V}^k+\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2},\frac{1}{{\mu }_2}\right)$ (10)

当 $\mathrm{shrink}\left(s,\gamma \right)=\mathrm{sign}\left(s\right)\odot \max \left\{\left|s\right|-\gamma ,0\right\}$，其中算术运算符是按分量计算。

3) 最小二乘问题的定义：目标函数由若干个函数的平方和构成。一般可以写成

$F\left(x\right)={\displaystyle \underset{i=1}{\overset{m}{\sum }}{f}_i^2}\left(x\right)$ (11)

其中 $x={\left(x_1,x_2,\cdots ,x_n\right)}^{{\rm T}}$ 是 ${ℝ}^n$ 中的点。我们假设

$f_i\left(x\right)=p_i^{{\rm T}}x-b_i,i=1,\cdots ,m$

其中 $p_i$ 是n维列向量， $b_i$ 是实数,我们可以用矩阵乘积形式来表达(11)式，令

$A=\left[\begin{array}{c}{p}_1^{{\rm T}}\\ ⋮\\ p_m^{{\rm T}}\end{array}\right]$， $b=\left[\begin{array}{c}{b}_1\\ ⋮\\ b_m\end{array}\right]$

$A$ 是 $m\times n$ 矩阵，b是m维列向量。则

$\begin{array}{c}F\left(x\right)={\displaystyle \underset{i=1}{\overset{m}{\sum }}{f}_i^2}\left(x\right)=\left(f_1\left(x\right),f_2\left(x\right),\cdots ,f_m\left(x\right)\right)\left[\begin{array}{c}{f}_1\left(x\right)\\ \begin{array}{c}{f}_2\left(x\right)\\ ⋮\end{array}\\ f_m\left(x\right)\end{array}\right]\\ ={\left(Ax-b\right)}^{{\rm T}}\left(Ax-b\right)\\ =x^{{\rm T}}{A}^{{\rm T}}Ax-2b^{{\rm T}}Ax+b^{{\rm T}}b\end{array}$

现在求 $F\left(x\right)$ 的平稳点。令 $\nabla F\left(x\right)=2A^{{\rm T}}Ax-2A^{{\rm T}}b=0$，则 $F\left(x\right)$ 的平稳点满足 $A^{{\rm T}}Ax=A^{{\rm T}}b$。设 $A$ 列满秩， $A^{{\rm T}}A$ 为n阶对称正定矩阵。由此得到目标函数 $F\left(x\right)$ 的平稳点： $\bar{x}={\left(A^{{\rm T}}A\right)}^{-1}{A}^{{\rm T}}b$。

求解 $V$ -子问题，利用最小二乘问题求解：

$V^{k+1}=\underset{V}{\text{argmin}}\left\{\frac{{\mu }_1}{2}{\Vert {\nabla }^{\alpha }{u}^{k+1}-V+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\Vert }_2^2+\frac{{\mu }_2}{2}{\Vert TV-W^{k+1}+\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2}\Vert }_2^2\right\}$,

对 $V$ 求偏导得

$-{\mu }_1\left({\nabla }^{\alpha }{u}^{k+1}-V+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\right)+{\mu }_{2}T\left(TV-W^{k+1}+\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2}\right)=0$,

合并同类项可得：

$\left({\mu }_{1}I+{\mu }_2{T}^2\right)V={\mu }_1\left({\nabla }^{\alpha }{u}^{k+1}+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\right)+{\mu }_{2}T\left(W^{k+1}-\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2}\right)$,

上式满足最小二乘问题，求解即可得

$V^{k+1}={\left({\left({\mu }_{1}I+{\mu }_2{T}^2\right)}^{{\rm T}}\left({\mu }_{1}I+{\mu }_2{T}^2\right)\right)}^{-1}{\left({\mu }_{1}I+{\mu }_2{T}^2\right)}^{{\rm T}}\left({\mu }_1\left({\nabla }^{\alpha }{u}^{k+1}+\frac{{\left({\lambda }_1^{{\rm T}}\right)}^k}{{\mu }_1}\right)+{\mu }_{2}T\left(W^{k+1}-\frac{{\left({\lambda }_2^{{\rm T}}\right)}^k}{{\mu }_2}\right)\right)$ (12)

对提出模型求解过程如下：

初始化阶段：输入初始图像 $u_0=f$，设置参数的初始值： $k=0$ ； $\eta =0.1$ ； $\alpha =1.5$ ； ${\mu }_1=0.1$ ； ${\mu }_2=0.2$，最大迭代次数 $\text{maxiter}=800$，迭代精度 $\epsilon ={10}^{-6}$。

算法迭代循环过程：

Step1：初始化 $k=1$， $\epsilon ={10}^{-6}$ ；

Step 2：通过(8)式更新子问题中的 $u^k$ ；

Step 3：通过(9)式更新子问题中的 $W^k$ ；

Step 4：通过(12)式更新子问题中的 $V^k$ ；

Step 6：通过(5)式更新拉格朗日乘子： ${\lambda }_1^k,{\lambda }_2^k$ ；

Step 7： $k=k+1$。

终止：若迭代精度 $\epsilon$ 小于10^-6或者迭代次数到达800则该算法终止，否则继续上述迭代循环过程。

4. 实验及分析

实验在LAPTOP-RETV7IRD Aspire A515-516Intel(R) Core(TM) i5-7200U CPU © 2.50 GHz 2.71 GHz RAM4.0G matlab2014a环境下进行。在实验中，我们使用了六幅标准测试图像，如图1所示，分别命名为woman、ultrasonic、CT、Einstein、barbara和pepper，如图4~9所示，为了验证本文算法对图像去噪的效果，本文中对六幅原始图像分别加入了噪声方差为15、20和25的高斯噪声。我们将提出的模型与传统的变分方法和扩散方法进行比较，包括分数阶全变分正则化模型(Fractional-Order Total Variation, FOTV)、高阶全正则化模型 [19] (High-Order Total Variation, HOTV)、和广义全变分 [20] (Total Generalized Variation, TGV)、三维块匹配滤波(Block-matching and 3D filtering, BM3D)、各向异性全变分模型(Anisotropic total variation, ATV)、分数阶各向异性扩散模型(Fractional-Order Anisotropic Diffusion, FOAD)和张量加权二阶变分模型 [14] (tensor weighted second order, TWSO)。所有这些方法的初始条件都设置为输入图像。本文利用图像的峰值信噪比(Peak Singal to Noise Ratio, PSNR)和结构相似性(Structual Similarity, SSIM)两个评价标准来评价去噪后的图像，两者值越大则说明去噪效果更好。当连续两次迭代的相对误差小于 $\epsilon ={10}^{-6}$ 或者迭代次数等于800则该算法终止。

woman ultrasonic CT Einstein Barbara pepper

Figure 1. Test image

图1. 测试图像

4.1. 对分数阶的阶数 $\alpha$ 的讨论

1) 阶数 $\alpha$ 的不自适应性

由图2的左图我们可以看出，在噪声方差为15的高斯噪声水平下，分数阶的阶数跟去噪图像的PSNR不是呈递增关系，由右图所示，在阶数 $\alpha =1.5$，去噪图像的PSNR值随着噪声水平的增大而减小，则说明分数阶阶数 $\alpha$ 具有不自适应性。

Figure 2. Sensitivity test of PSNR value with fractional order and noise variance

图2. PSNR值随分数阶阶数和噪声方差变化的灵敏度试验

2) 阶数 $\alpha$ 与图像纹理的关系

由图3所示，在相同的高斯噪声水平下，对于含有纹理细节信息较少的图像，其去噪图像的PSNR值在分数阶阶数 $\alpha \ge 1.5$ 时，峰值信噪比最优，对于含有纹理细节信息较多的图像，其去噪图像的PSNR值在分数阶阶数 $\alpha \le 1.4$ 时，峰值信噪比最优。说明图像纹理信息越多，去噪模型的分数阶阶数越小。

Figure 3. Comparison of PSNR values with fractional order, left: images with less texture information; right: an image with more texture information

图3. PSNR值随分数阶阶数而变化的对比，左：含有较少纹理信息的图像；右：含有较多纹理信息的图像

4.2. 图像去噪模型的对比效果

1) 基于变分的图像去噪模型的对比效果

由图4~6可以看出，TV模型存在明显的阶梯效应，HOTV和TGV由于涉及高阶导数，可以减少阶梯伪影，TGV复原后的图像不连续附近的区域留下了一些噪音。FOTV可以有效保留图像的纹理细节信息，然而复原后肺部CT图像的边缘轮廓不清晰；经HOTV复原的图像可看出肺部器官的分界部分不清晰，而本文的TWFO模型不存在边缘过模糊，且能较好地复原图像的纹理信息，woman图像脸部轮廓更为清晰。且由表1可知，TWFO复原后的图像的PSNR值和SSIM值最高，其PSNR值和SSIM值分别高于TGV 1.64dB和0.02，进一步验证了本文模型的有效性。

含噪图像 HOTV FOTV TGV BM3D 本文模型

Figure 4. Comparison of denoising effects with noise variance of 15

图4. 在噪声方差为15的去噪效果对比

含噪图像 HOTVFOTVTGVBM3D 本文模型

Figure 5. Comparison of denoising effects with noise variance of 20

图5. 在噪声方差为20的去噪效果对比

含噪图像 HOTV FOTV TGVBM3D 本文模型

Figure 6. Comparison of denoising effects with noise variance of 25

图6. 在噪声方差为25的去噪效果对比

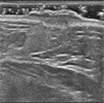
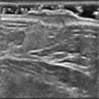
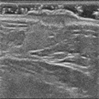
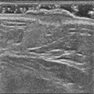
Table 1. Comparison of PSNR and SSIM of image denoising results under different noise levels (PSNR unit: dB)

表1. 图像在不同噪声水平下的去噪结果的PSNR和SSIM对比(PSNR单位：dB)

2) 基于扩散方程的图像去噪模型的对比效果

由图7~9可看出，与其他模型相比，本文的模型通常产生更清晰的结果。即TWFO正则化可以很好地保持图像的结构和边缘，并产生令人满意的去噪结果。ATV和FOAD复原后的图片，超声图像血管部分的失真较大，且边缘部分存在一定的模糊，HOAD复原后的图像的不连续区域仍存在一些噪声，ATV重建后图像可以看到明显的“阶梯现象”。而TWFO对血管的轮廓复原效果最好，由表2可知本文模型复原图像的PSNR值和SSIM值优于其他模型，由客观指标可以看出，TWFO有效抑制阶梯效应，保留图像边缘以及较好地复原图像纹理细节信息。

含噪图像 ATV FOAD TWSO本文模型

Figure 7. Comparison of denoising effects with noise variance of 15

图7. 在噪声方差为15的去噪效果对比

含噪图像 ATV FOAD TWSO 本文模型

Figure 8. Comparison of denoising effects with noise variance of 20

图8. 在噪声方差为20的去噪效果对比

含噪图像 ATVFOADTWSO 本文模型

Figure 9. Comparison of denoising effects with noise variance of 25

图9. 在噪声方差为25的去噪效果对比

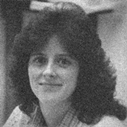
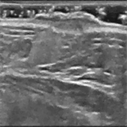
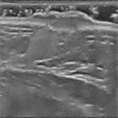
Table 2. Comparison of PSNR and SSIM of image denoising results under different noise levels (PSNR unit: dB)

表2. 图像在不同噪声水平下的去噪结果的PSNR和SSIM对比(PSNR单位：dB)

3) 局部区域放大的对比结果

由图10和图11所示，当噪声方差较小时，本文模型和对比模型均有良好的去噪效果，且BM3D处理后的图片具有一定平滑效果，但结构相似性值偏低，ATV复原的图像处存在明显的块伪影，HOTV、FOTV和TGV这3种方法复原的图像无法完好保留图像边缘信息；TWFO模型较好地保留图像边缘或纹理等细节结构，抑制阶梯效应。

HOTV FOTV TGV BM3DATV FOAD TWSO 本文模型

Figure 10. Comparison of local amplification area of denoising effect of woman image with noise variance of 15

图10. 在噪声方差为15的woman图像去噪效果的局部放大区域对比

HOTV FOTV TGV BM3DATVFOAD TWSO 本文模型

Figure 11. Comparison of local amplification area of denoising effect of CT image with noise variance of 20

图11. 在噪声方差为20的CT图像去噪效果的局部放大区域对比

HOTVFOTV TGV BM3DATVFOAD TWSO 本文模型

Figure 12. Comparison of local amplification area of denoising effect of pepper image with noise variance of 25

图12. 在噪声方差为25的pepper图像去噪效果的局部放大区域对比

由图12所示，当噪声方差较大时，其他七种对比模型的SSIM值均有显著降低，造成图片中有用信息基本无法识别，边缘破坏，细节纹理信息模糊。本文模型可以有效提高这一点，在保持良好的去噪效果，同时最大限度地保留图像信息，以添加高斯噪声方差25为例，结果明显优于其他算法。

4.3. 模型在数据库Set5和Set14下的去噪效果

由图13相比之下，本文模型在噪声增加的情况下产生了更令人满意的视觉结果，其PSNR和SSIM在所有情况下都保持最高，因为在TWFO中引入张量提供了更丰富的邻域信息，由表3可得，本文模型对应的平均PSNR值和SSIM值高于其他对比模型，说明了本文模型复原的图像结构细节普遍优于其他对比模型，验证了本文模型的有更好的图像复原性能。

Table 3. Comparison of average PSNR value and SSIM value of noise results in Set5 and Set14 databases under Gaussian noise with different intensity (PSNR unit: dB)

表3. Set5和Set14数据库在含不同强度的高斯噪声下去噪结果的平均PSNR值和SSIM值对比(PSNR单位：dB)

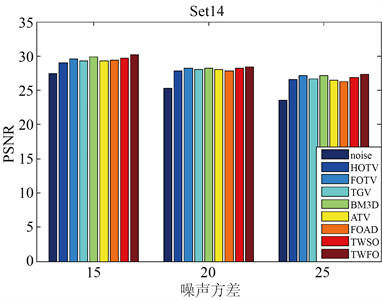
Figure 13. Quantitative image quality evaluation of Gaussian noise removal in Table 3

图13. 表3中高斯噪声去除的定量图像质量评价

5. 结论

本文提出了一种张量加权分数阶变分模型，利用分数阶的Jacobian矩阵形式和一个各向异性张量的乘积的Frobenius范数，提出了一种新的正则化子，使分数阶变分成为一个有效集成方向信息的非线性各向异性分数阶模型，同时较好地保留了图像的纹理细节、不连续性和结构，平滑区域与TV模型不同，TWFO模型不存在边缘附近的假边缘，且抑制阶梯效应。

基金项目

基金项目：国家自然科学基金(62061016, 61561019)资助项目，湖北民族大学研究生(MYK2022010)项目。

NOTES

^*通讯作者。