基于事件触发的非线性多智能体系统二分一致性跟踪控制

Event-Triggered Bipartite Consensus Tracking Control for Nonlinear Multi-Agent Systems

摘要: 针对非线性多智能体系统，研究了符号有向图下的基于事件触发的二分一致性跟踪控制问题。分别给出了集中式和分布式的事件触发控制协议。主要利用矩阵理论、代数图论和Lyapunov稳定性理论，证明了所给的控制协议能够解决二分一致性跟踪控制问题，并且不存在Zeno行为。采用事件触发策略，能够有效减少控制输入的更新次数，达到节约网络带宽和降低通信成本的目的。最后，仿真结果验证了理论结果的有效性。

Abstract: This paper investigates the bipartite consensus tracking control problem of nonlinear multi-agent systems under the signed directed graph. The centralized and distributed event-triggered control protocols are presented respectively. By using matrix theory algebraic graph theory and Lyapunov stability theory, it is proved that the proposed control protocol can solve the bipartite consensus tracking control problem, and there is no Zeno behavior. The event-triggered strategy can effectively reduce the update times of control input, and achieve the purpose of saving network bandwidth and reducing communication cost. Finally, the simulation results verify the validity of the theoretical results.

1. 引言

实际生活中，多智能体系统在许多领域都有广泛的应用，例如在军事、生物以及电力系统等方面都有着重要的作用 [1] [2] [3]。其中，一致性问题作为多智能体相互协作的基础，一直受到大量研究者的重点关注。一致性是指多智能体系统中的个体在局部协作和相互通信下，调整自己的行为，最终使得每个个体均能达到相同的状态 [4]。而一致性问题也被广泛应用于机器人编队、集聚控制等方面 [5] [6]，也是目前控制学科的一个研究重点。文献 [7] 研究了具有固定拓扑和切换拓扑的一阶线性多智能体系统一致性问题。文献 [8] 研究了带有领导者的线性多智能体系统的一致性问题。在上述文献中，大多只考虑了智能体之间仅存在合作关系，即最终所有智能体状态保持一致。

但是在实际场景中，智能体之间往往有合作关系也有对抗关系，比如自然界中两个物种之间的生存与对抗，竞技比赛中的对抗关系等。因此研究合作与对抗共存的网络拓扑更具有实际意义。合作与对抗的交互关系可以用正负权重的邻接矩阵表示，也就是可以用符号图表示，即所有智能体可以分为两组，这两组智能体最终收敛到大小相同但符号相反的一致性值。针对合作与对抗关系下的多智能体系统，文献 [9] 提出了二分一致性而不再是一致性，针对线性系统和非线性系统两种情况，研究了系统达到二分一致性的充要条件。文献 [10] 研究了基于结构平衡的符号网络的二分一致性问题，其结构平衡简单来说是指符号图中的节点集可以分为两个子集，每个子集内部节点之间的权重为正值，子集之间的节点连接处的权重为负值。文献 [11] 研究了非线性多智能体系统在符号有向图下的二分一致性问题。文献 [12] 研究了单领导者的线性系统的二分一致性问题。

对于一致性问题，传统的处理方法是对邻居信息进行周期采样，虽然此方法便于理论分析，但是却忽略了通信带宽和计算资源是有限的，因此采用传统方法会造成通信资源浪费这一问题。为了减少通信资源不必要的浪费，文献 [13] 提出了一种新的事件触发策略，基于事件触发控制协议的特点是：只有当一个特定事件发生即满足事件驱动函数时，才进行一次信息采样。因此采用事件触发的控制协议可以有效降低通信资源的消耗。现如今，众多学者在研究多智能体系统一致性问题中，已将事件触发策略有效应用。如文献 [14] 将事件触发策略应用到一阶多智能体系统一致性的研究当中。文献 [15] 研究了基于事件触发下的固定时间的多智能体系统一致性问题。文献 [16] 研究了基于事件触发下的二阶多智能体系统的一致性问题。文献 [17] 研究了基于事件触发下的领导跟随一致性问题。文献 [18] 研究了基于事件触发下的线性多智能体系统二分一致性问题。

本文在已有研究的基础上，考虑了有领导者非线性多智能体系统在符号有向图拓扑下以及事件驱动机制下的二分一致性跟踪控制问题。研究了集中式和分布式事件触发控制方法，利用矩阵理论、代数图论和Lyapunov稳定性理论得到了系统达到二分一致性跟踪控制的充分条件，同时验证了在两种控制协议下均不存在Zeno现象的发生。

符号标记：为便于本文数学推导，介绍以下数学符号定义和说明。

本文中R表示实数集合。设A为对称阵， ${\lambda }_{\min }\left(A\right)$ 表示矩阵A的最小特征值， $A>0$ 表示A为正定矩阵， $1_n={\left[1,1,\cdots ,1\right]}^{\text{T}}\in R^n$。

2. 预备知识和问题描述

2.1. 图论

多智能体的通信拓扑可以用加权有向符号图 $G=\left(V,E,A\right)$ 表示，其中 $V=\left\{v_1,v_2,\cdots ,v_n\right\}$ 表示所有节点的集合， $E\in V\times V$ 表示所有边的集合， $A=\left[a_{ij}\right]\in R^{n\times n}$ 表示符号图G所对应的加权邻接矩阵。对于符号有向图G， $\left(v_i,v_j\right)$ 表示一条从节点 $v_i$ 到节点 $v_j$ 的有向边，并且所对应的加权邻接矩阵A中元素 $a_{ij}$ 非零。 $E^{+}$ 和 $E^{-}$ 分别表示正边集合和负边集合，即 $E^{+}=\left\{\left(i,j\right)|a_{ij}>0\right\}$ 以及 $E^{-}=\left\{\left(i,j\right)|a_{ij}<0\right\}$，同时 $E^{+}\cup E^{-}=E$。若在符号图中任意两个节点都存在一条有向路径，则称图G为强连通的。若智能体i和智能体j之间的信息交互是协作的，则 $a_{ij}>0$ ；若信息交互是对抗的，则 $a_{ij}<0$。在本文中将不考虑带有自环的符号图，即 $a_{ii}=0$。显然，在符号图G中，邻接矩阵A不再是非负矩阵。符号图G的度矩阵 $\Delta =diag\left\{{\Delta }_1,{\Delta }_2,\cdots ,{\Delta }_n\right\}$，

${\Delta }_i={\displaystyle \underset{j\in N_i}{\sum }\left|a_{ij}\right|}$。符号图G的Laplacian矩阵L定义为 $L=\Delta -{\rm A}$。若G中所有边的权值全为正值，则称之为正符号图。

定义1 [4]：在符号图G中，若存在互不相交的节点集 $V_1$ 和 $V_2$，其中 $V_1\cup V_2=V$， $V_1\cap V_2=\varnothing$，同时满足以下两个条件：

1)若 $\forall v_i,v_j\in V_l\left(l\in \left\{1,2\right\}\right)$，则 $a_{ij}\ge 0$ ；

2)若 $\forall v_i\in V_l,v_j\in V_q,l\ne q\left(l,q\in \left\{1,2\right\}\right)$，则 $a_{ij}\le 0$。

则称符号图G是结构平衡的，否则称结构不平衡。

引理1 [9]：当符号图是结构平衡的，则存在一个变换矩阵D，使得DAD为非负矩阵，其中 $D=diag\left\{{\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n,{\epsilon }_{n+1}\right\}$， $\epsilon \in \left\{-1,1\right\}$。

引理2 [19]：任意 $a,b\in R$，对于任意大于零的数 $\theta$，则满足 $\left|ab\right|\le \frac{\theta }{2}{a}^2+\frac{1}{2\theta }{b}^2$。

2.2. 问题描述

本文中考虑由 $n+1$ 个智能体所构成的系统，其中包括n个跟随者与一个领导者。跟随者的动力学方程可以描述为：

${\stackrel{\dot{}}{x}}_i\left(t\right)=f\left(x_i\left(t\right),t\right)+u_i\left(t\right),i=1,2,\cdots ,n$ (1)

其中， $x_i\left(t\right)\in R$ 表示跟随者的状态， $u_i\left(t\right)\in R$ 表示控制输入，f表示非线性连续函数。

领导者的动力学方程可以描述为：

${\stackrel{\dot{}}{x}}_{n+1}\left(t\right)=f\left(x_{n+1}\left(t\right),t\right)$ (2)

其中， $x_{n+1}\left(t\right)\in R$ 表示领导者的状态。

定义2：针对跟随者系统(1)与领导者系统(2)，若存在控制输入 $u_i\left(t\right)$，使得对任意初始状态 $x_i\left(0\right)$ $\left(i=1,2,\cdots ,n\right)$ 与 $x_{n+1}\left(0\right)$，都满足以下条件：

$\underset{t\to +\infty }{\lim }\left|x_i\left(t\right)-x_{n+1}\left(t\right)\right|=0,\forall i\in V_1$

$\underset{t\to +\infty }{\lim }\left|x_i\left(t\right)+x_{n+1}\left(t\right)\right|=0,\forall i\in V_2$

则称控制输入 $u_i\left(t\right)$ 能解决二分一致性跟踪控制问题。

二分一致性跟踪控制意味着随着时间的推移，系统中的跟随智能体可分为两组，一组跟随智能体收敛到领导者的状态，另一组跟随智能体收敛到领导者状态的相反数。

3. 主要结果

3.1. 集中式事件触发二分一致性

本小节研究如下的控制协议：

$u_i\left(t\right)=-\alpha y_i\left(t_k\right)$ (3)

其中， $\alpha$ 表示控制增益， $t_k$ 表示智能体i的触发时刻， $y_i$ 的定义如下：

$y_i\left(t\right)={\displaystyle \underset{j=1}{\overset{n+1}{\sum }}\left|a_{ij}\right|}\left(x_i\left(t\right)-sign\left(a_{ij}\right)x_j\left(t\right)\right),i=1,2,\cdots ,n$ (4)

其中， $sign(·)$ 为符号函数。

定义智能体i的状态测量误差为：

$e_i\left(t\right)=\alpha y_i\left(t_k\right)-\alpha y_i\left(t\right),i=1,2,\cdots ,n$ (5)

在本文中，假设领导者只发送信息，则图G的Laplacian矩阵L可以写成分块的形式：

$L=\left[\begin{array}{cc}{L}_1& L_2\\ 0& 0\end{array}\right]$

其中， $L_1\in R^{n\times n}$， $L_2\in R^{n\times 1}$。

定义向量： $x\left(t\right)={\left(x_1\left(t\right),x_2\left(t\right),\cdots ,x_n\left(t\right)\right)}^{\text{T}}$， $e\left(t\right)={\left(e_1\left(t\right),e_2\left(t\right),\cdots ,e_n\left(t\right)\right)}^{\text{T}}$，

$y\left(t\right)={\left(y_1\left(t\right),y_2\left(t\right),\cdots ,y_n\left(t\right)\right)}^{\text{T}}$， $f\left(x\left(t\right),t\right)={\left(f\left(x_1\left(t\right),t\right),f\left(x_2\left(t\right),t\right),\cdots ,f\left(x_n\left(t\right),t\right)\right)}^{\text{T}}$。

则式子(4)可以进一步表示为：

$y\left(t\right)=L_{1}x\left(t\right)+L_2{x}_{n+1}\left(t\right)$ (6)

令 $\tilde{y}\left(t\right)=D_{1}y\left(t\right)$， $\tilde{e}\left(t\right)=D_{1}e\left(t\right)$。

其中 $D_1=diag\left\{{\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n\right\}$。结合式子(6)可进一步表示为：

$\tilde{y}\left(t\right)=D_1{L}_{1}x\left(t\right)+D_1{L}_2{x}_{n+1}\left(t\right)$ (7)

假设1：非线性函数 $f\left(x_i\left(t\right),t\right)$ 满足利普希兹条件：

$\left|f\left(x_1\left(t\right),t\right)\pm f\left(x_2\left(t\right),t\right)\right|\le l\left|x_1\left(t\right)\pm x_2\left(t\right)\right|$

其中， $x_1\left(t\right),x_2\left(t\right)\in R$，l为大于0的常数。

假设2：假设系统的通信拓扑G为结构平衡的且包含生成树，领导者为根节点。

引理3 [20]：在正符号图中，若G包含生成树，则矩阵 $L_1$ 可逆且 $-L_1^{-1}{L}_2=1_n$。

引理4 [21]：若假设2成立，则 $D_1{L}_1{D}_1$ 是非奇异M矩阵，且存在正定矩阵 $P=diag\left({\xi }_1,{\xi }_2,\cdots ,{\xi }_N\right)$，使得：

$P{D}_1{L}_1{D}_1+D_1{L}_1^{\text{T}}{D}_{1}P>0$.

接下来给出本节的主要结论：

定理1：针对系统(1)与系统(2)，智能体的事件触发函数可以设计为：

$f\left(e\right)=\Vert \tilde{e}\left(t\right)\Vert -\frac{\sigma \left(\alpha {\lambda }_0-2l\Vert P\Vert \right)}{2\Vert P\Vert \cdot \Vert L_1\Vert }\cdot \Vert \tilde{y}\left(t\right)\Vert$ (8)

其中， $0<\sigma <1$，控制增益 $\alpha$ 满足： $\alpha >\frac{2l\Vert P\Vert }{{\lambda }_0}$， ${\lambda }_0={\lambda }_{\min }\left(P{D}_1{L}_1{D}_1+D_1{L}_1^{\text{T}}{D}_{1}P\right)$，P是引理4中的正定矩阵。

那么在控制协议(3)的作用下，系统(1)与系统(2)可以达到二分一致性跟踪控制。

证明：构造如下Lyapunov函数：

$V\left(t\right)=\tilde{y}{\left(t\right)}^{\text{T}}P\tilde{y}(\; t\; )$

则 $\stackrel{\dot{}}{V}\left(t\right)=2{\tilde{y}}^{\text{T}}P\stackrel{\dot{}}{\tilde{y}}$。

根据引理3，式(7)可以进一步表示为：

$\begin{array}{c}\tilde{y}\left(t\right)=D_1{L}_1{D}_1{D}_1^{-1}x\left(t\right)+D_1{L}_2{D}_2{D}_2^{-1}{x}_{n+1}\left(t\right)\\ =D_1{L}_1{D}_1\left[D_{1}x\left(t\right)+{\left(D_1{L}_1{D}_1\right)}^{-1}\left(D_1{L}_2{D}_2\right)D_2^{-1}{x}_{n+1}\left(t\right)\right]\\ =D_1{L}_1{D}_1\left[D_{1}x\left(t\right)-1_n{D}_2^{-1}{x}_{n+1}\left(t\right)\right]\end{array}$ (9)

其中， $D_2={\epsilon }_{n+1}$。结合系统(1)与系统(2)对 $\tilde{y}$ 进行求导，可得：

$\begin{array}{c}\stackrel{\dot{}}{\tilde{y}}\left(t\right)=D_1{L}_1\stackrel{\dot{}}{x}\left(t\right)+D_1{L}_1{\stackrel{\dot{}}{x}}_{n+1}\left(t\right)\\ =D_1{L}_1\left[f\left(x\left(t\right),t\right)+u\left(t\right)\right]+D_1{L}_{2}f\left(x_{n+1}\left(t\right)\right)\\ =D_1{L}_1\left[-\alpha y\left(t\right)-e\left(t\right)+f\left(x\left(t\right),t\right)\right]+D_1{L}_2{D}_2{D}_2^{-1}f\left(x_{n+1}\left(t\right),t\right)\\ =-\alpha D_1{L}_1{D}_1\tilde{y}\left(t\right)-D_1{L}_1{D}_1{D}_{1}e\left(t\right)+D_1{L}_1{D}_1{D}_{1}f\left(x\left(t\right),t\right)+D_1{L}_2{D}_2{D}_2^{-1}f\left(x_{n+1}\left(t\right),t\right)\\ =-\alpha D_1{L}_1{D}_1\tilde{y}\left(t\right)-D_1{L}_1{D}_1{D}_{1}e\left(t\right)+D_1{L}_1{D}_1\left[D_{1}f\left(x\left(t\right),t\right)-1_n{D}_2^{-1}f\left(x_{n+1},t\right)\right]\end{array}$ (10)

所以 $\stackrel{\dot{}}{V}\left(t\right)$ 可进一步表示为：

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)=2{\tilde{y}}^{\text{T}}P\left[-\alpha D_1{L}_1{D}_1\tilde{y}\left(t\right)-D_1{L}_1{D}_1{D}_{1}e\left(t\right)+D_1{L}_1{D}_1{D}_{1}f\left(x\left(t\right),t\right)-1_n{D}_2^{-1}f\left(x_{n+1}\left(t\right),t\right)\right]\\ =-2\alpha {\tilde{y}}^{\text{T}}P{D}_1{L}_1{D}_1\tilde{y}\left(t\right)-2{\tilde{y}}^{\text{T}}P{D}_1{L}_1{D}_1{D}_{1}e\left(t\right)+2{\tilde{y}}^{\text{T}}P{D}_1{L}_1{D}_1\left[D_{1}f\left(x\left(t\right),t\right)-1_n{D}_2^{-1}f\left(x_{n+1}\left(t\right),t\right)\right]\\ =-\alpha {\tilde{y}}^{\text{T}}\left(P{D}_1{L}_1{D}_1+D_1{L}_1^{\text{T}}{D}_{1}P\right)\tilde{y}\left(t\right)-2{\tilde{y}}^{\text{T}}P{D}_1{L}_1{D}_1{D}_{1}e\left(t\right)+2{\tilde{y}}^{\text{T}}P{D}_1{L}_1{D}_1{D}_{1}e\left(t\right)\\ +2{\tilde{y}}^{\text{T}}P{D}_1{L}_1{D}_1\left[D_{1}f\left(x\left(t\right),t\right)-1_n{D}_2^{-1}f\left(x_{n+1}\left(t\right),t\right)\right]\end{array}$

所以根据引理4与假设1可将上式表示为：

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)\le -\alpha {\lambda }_0{\Vert \tilde{y}\left(t\right)\Vert }^2+2\Vert \tilde{y}\left(t\right)\Vert \cdot \Vert P\Vert \cdot \Vert L_1\Vert \cdot \Vert \tilde{e}\left(t\right)\Vert +2\Vert \tilde{y}\left(t\right)\Vert \cdot \Vert P\Vert \cdot l\cdot \Vert \tilde{y}\left(t\right)\Vert \\ =-\alpha {\lambda }_0{\Vert \tilde{y}\left(t\right)\Vert }^2+2\Vert \tilde{y}\left(t\right)\Vert \cdot \Vert P\Vert \cdot \Vert L_1\Vert \cdot \Vert \tilde{e}\left(t\right)\Vert +2l{\Vert \tilde{y}\left(t\right)\Vert }^2\cdot \Vert P\Vert \\ =-\left(\alpha {\lambda }_0-2l\Vert P\Vert \right){\Vert \tilde{y}\left(t\right)\Vert }^2+2\Vert P\Vert \cdot \Vert L_1\Vert \cdot \Vert \tilde{e}\left(t\right)\Vert \cdot \Vert \tilde{y}\left(t\right)\Vert \end{array}$ (11)

由式(8)可以得到：

$\Vert \tilde{e}\left(t\right)\Vert \le \frac{\sigma \left(\alpha {\lambda }_0-2l\Vert P\Vert \right)}{2\Vert P\Vert \cdot \Vert L_1\Vert }\cdot \Vert \tilde{y}\left(t\right)\Vert$

所以可以得到：

$\stackrel{\dot{}}{V}\le \left(\sigma -1\right)\left(\alpha {\lambda }_0-2l\Vert P\Vert \right){\Vert \tilde{y}\left(t\right)\Vert }^2$

由条件可知， $\stackrel{\dot{}}{V}\left(t\right)<0$，所以可以得到： $\underset{t\to +\infty }{\lim }\tilde{y}\left(t\right)=0$，从而使得系统(1)与系统(2)能够达到二分一致性跟踪控制。

定理2：针对跟随者系统(1)与领导者系统(2)，若限定事件触发函数(8)成立，则在控制协议(3)作用下，智能体在任意两个连续事件触发时刻之间的间隔 $t_{k+1}-t_k$ 不小于：

$\tau =\frac{2\alpha \sigma l\Vert P\Vert -\sigma a^2{\lambda }_0}{\left(2\sigma l\Vert P\Vert -\sigma \alpha {\lambda }_0-2\alpha \Vert P\Vert \cdot \Vert L_1\Vert \right)\left(\alpha l+{\alpha }^2\Vert L_1\Vert \right)}$

证明：由事件触发控制原理知，系统任意两个连续事件触发时刻之间的间隔时间为： $\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }$ 从0增长到 $\frac{\sigma \left(\alpha {\lambda }_0-2l\Vert P\Vert \right)}{2\Vert P\Vert \cdot \Vert L_1\Vert }$ 所需要的时间，记为 $\tau$。

对 $\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }$ 求导可得：

$\begin{array}{c}\frac{\text{d}\Vert \tilde{e}\left(t\right)\Vert }{\text{d}t\Vert \tilde{y}\left(t\right)\Vert }=\frac{\text{d}{\left({\tilde{e}}^{\text{T}}\left(t\right)\tilde{e}\left(t\right)\right)}^{1/2}}{\text{d}t{\left({\tilde{y}}^{\text{T}}\left(t\right)\tilde{y}\left(t\right)\right)}^{1/2}}\\ =\frac{{\tilde{e}}^{\text{T}}\left(t\right)\stackrel{\dot{}}{\tilde{e}}\left(t\right)\frac{1}{\Vert \tilde{e}\left(t\right)\Vert }\Vert \tilde{y}\left(t\right)\Vert -{\tilde{y}}^{\text{T}}\left(t\right)\stackrel{\dot{}}{\tilde{y}}\left(t\right)\frac{1}{\Vert \stackrel{\dot{}}{\tilde{y}}\left(t\right)\Vert }\Vert \tilde{e}\left(t\right)\Vert }{{\Vert \tilde{y}\left(t\right)\Vert }^2}\\ =\frac{{\tilde{e}}^{\text{T}}\left(t\right)\stackrel{\dot{}}{\tilde{e}}\left(t\right)}{\Vert \tilde{e}\left(t\right)\Vert \cdot \Vert \tilde{y}\left(t\right)\Vert }-\frac{\Vert \tilde{e}\left(t\right)\Vert {\tilde{y}}^{\text{T}}\left(t\right)\stackrel{\dot{}}{\tilde{y}}\left(t\right)}{{\Vert \tilde{y}\left(t\right)\Vert }^3}=\frac{-\alpha {\tilde{e}}^{\text{T}}\left(t\right)\stackrel{\dot{}}{\tilde{y}}\left(t\right)}{\Vert \tilde{e}\left(t\right)\Vert \cdot \Vert \tilde{y}\left(t\right)\Vert }-\frac{\Vert \tilde{e}\left(t\right)\Vert {\tilde{y}}^{\text{T}}\left(t\right)\stackrel{\dot{}}{\tilde{y}}\left(t\right)}{{\Vert \tilde{y}\left(t\right)\Vert }^3}\\ \le \frac{\alpha \Vert \stackrel{\dot{}}{\tilde{y}}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }+\frac{\Vert \tilde{e}\left(t\right)\Vert \cdot \Vert \stackrel{\dot{}}{\tilde{y}}\left(t\right)\Vert }{{\Vert \tilde{y}\left(t\right)\Vert }^2}=\left(\alpha +\frac{\Vert \tilde{e}(t)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\right)\frac{\Vert \stackrel{\dot{}}{\tilde{y}}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\end{array}$

所以根据式(10)可进一步表示为：

$\begin{array}{c}\frac{\text{d}\Vert \tilde{e}\left(t\right)\Vert }{\text{d}t\Vert \tilde{y}\left(t\right)\Vert }=\left(\alpha +\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\right)\frac{\Vert \stackrel{\dot{}}{\tilde{y}}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\\ \le \left(\alpha +\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\right)\frac{\alpha \Vert L_1\Vert \cdot \Vert \tilde{y}\left(t\right)\Vert +\Vert L_1\Vert \cdot \Vert \tilde{e}\left(t\right)\Vert +l\Vert \tilde{y}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\\ =\left(\alpha +\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\right)\left(\alpha \Vert L_1\Vert +\Vert L_1\Vert \frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }+l\right)\\ =l\left(\alpha +\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }\right)+\Vert L_1\Vert {\left(\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }+\alpha \right)}^2\\ =\alpha l\left(1+\frac{\Vert \tilde{e}\left(t\right)\Vert }{\alpha \Vert \tilde{y}\left(t\right)\Vert }\right)+{\alpha }^2\Vert L_1\Vert {\left(\frac{\Vert \tilde{e}\left(t\right)\Vert }{\alpha \Vert \tilde{y}\left(t\right)\Vert }+1\right)}^2\end{array}$ (12)

根据控制增益 $\alpha$ 满足的范围，所以可得： $1+\frac{\Vert \tilde{e}\left(t\right)\Vert }{\alpha \Vert \tilde{y}\left(t\right)\Vert }\ge 1$，且 $\left(1+\frac{\Vert \tilde{e}\left(t\right)\Vert }{\alpha \Vert \tilde{y}\left(t\right)\Vert }\right)\le {\left(1+\frac{\Vert \tilde{e}\left(t\right)\Vert }{\alpha \Vert \tilde{y}\left(t\right)\Vert }\right)}^2$。

所以根据式(12)可得：

$\frac{\text{d}\Vert \tilde{e}\left(t\right)\Vert }{\text{d}t\Vert \tilde{y}\left(t\right)\Vert }\le \left(\alpha l+{\alpha }^2\Vert L_1\Vert \right){\left(1+\frac{\Vert \tilde{e}\left(t\right)\Vert }{\alpha \Vert \tilde{y}\left(t\right)\Vert }\right)}^2$ (13)

令 $z=\frac{\Vert \tilde{e}\left(t\right)\Vert }{\Vert \tilde{y}\left(t\right)\Vert }$，则有：

$\stackrel{\dot{}}{z}\le \left(\alpha l+{\alpha }^2\Vert L_1\Vert \right){\left(1+\frac{1}{a}z\right)}^2$ (14)

且z满足 $z\le \varphi \left(t,{\varphi }_0\right)$，这里 $\varphi \left(t,{\varphi }_0\right)$ 是方程 $\left(\alpha l+{\alpha }^2\Vert L_1\Vert \right){\left(1+\frac{1}{a}\varphi \right)}^2$， $\varphi \left(0,{\varphi }_0\right)={\varphi }_0$ 的解。

由式(8)知方程的解满足：

$\varphi \left(\tau ,0\right)=\frac{\sigma \left(\alpha {\lambda }_0-2l\Vert P\Vert \right)}{2\Vert P\Vert \cdot \Vert L_1\Vert }$

求解方程可得：

$\tau =\frac{2\alpha \sigma l\Vert P\Vert -\sigma a^2{\lambda }_0}{\left(2\sigma l\Vert P\Vert -\sigma \alpha {\lambda }_0-2\alpha \Vert P\Vert \cdot \Vert L_1\Vert \right)\left(\alpha l+{\alpha }^2\Vert L_1\Vert \right)}$

所以定理得证。

3.2. 分布式事件触发二分一致性

本小节研究如下的控制协议：

$u_i\left(t\right)=-\alpha y_i\left(t_k^i\right)$ (15)

其中， $\alpha$ 表示控制增益， $t_k^i$ 表示智能体i的触发时刻， $y_i$ 的定义如下：

$y_i\left(t\right)={\displaystyle \underset{j=1}{\overset{n+1}{\sum }}\left|a_{ij}\right|}\left(x_i\left(t_k^i\right)-sign\left(a_{ij}\right)x_j\left(t_{k^{\prime }}^j\right)\right),i=1,2,\cdots ,n$ (16)

其中， $t_{k^{\prime }}^j=\arg \underset{l\in N,t\ge t_l^j}{\min }\left\{t-t_l^j\right\}$。

定义每个智能体的状态测量误差为：

$e_i\left(t\right)=\alpha y_i\left(t_k^i\right)-\alpha y_i\left(t\right),i=1,2,\cdots ,n$ (17)

则式(17)可以进一步表示为：

$u_i\left(t\right)=-\alpha y_i\left(t\right)-e_i\left(t\right)$ (18)

根据 $\tilde{y}\left(t\right)=D_{1}y\left(t\right)$， $\tilde{e}\left(t\right)=D_{1}e\left(t\right)$， $D_1=diag\left\{{\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n\right\}$。

则 $\tilde{y}\left(t\right)$ 可进一步表示为：

$\tilde{y}\left(t\right)=D_1{L}_{1}x\left(t\right)+D_1{L}_2{x}_{n+1}(\; t\; )$

接下来给出本节的主要结论：

定理3：针对系统(1)与系统(2)，智能体的事件触发函数可以设计为：

$f\left(e\right)={\tilde{e}}_i^2-\frac{\theta {\sigma }_{i}K}{2{\Delta }_i{\xi }_{\max }}{\tilde{y}}_i^2$ (19)

其中， $0<{\sigma }_i<1$， $0<\theta$，控制增益 $\alpha$ 足： $\alpha >\frac{2l\Vert P\Vert +2{\xi }_{\max }{\Delta }_i\theta }{{\lambda }_0}$， $K=\alpha {\lambda }_0-2l\Vert P\Vert -2{\xi }_{\max }{\Delta }_i\theta$，

${\lambda }_0={\lambda }_{\min }\left(P{D}_1{L}_1{D}_1+D_1{L}_1^{\text{T}}{D}_{1}P\right)$， ${\xi }_{\max }$ 为引理4中正定矩阵P的最大元素。

那么在控制协议(15)的作用下，系统(1)与系统(2)可以达到二分一致性跟踪控制。

证明：构造如下Lyapunov函数：

$V\left(t\right)=\tilde{y}{\left(t\right)}^{\text{T}}P\tilde{y}(\; t\; )$

则

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)=2{\tilde{y}}^{\text{T}}P\stackrel{\dot{}}{\tilde{y}}\\ =2{\tilde{y}}^{\text{T}}P\left[-\alpha D_1{L}_1{D}_1\tilde{y}\left(t\right)-D_1{L}_1{D}_1{D}_{1}e\left(t\right)\right]+2{\tilde{y}}^{\text{T}}P\left[D_1{L}_1{D}_1{D}_{1}f\left(x\left(t\right),t\right)-1_n{D}_2^{-1}f\left(x_{n+1}\left(t\right),t\right)\right]\\ \le -\alpha {\lambda }_0{\Vert \tilde{y}\left(t\right)\Vert }^2+2l\Vert P\Vert \cdot {\Vert \tilde{y}\left(t\right)\Vert }^2+2{\tilde{y}}^{\text{T}}P{L}_1\tilde{e}\left(t\right)\\ =-\left(\alpha {\lambda }_0-2l\Vert P\Vert \right){\Vert \tilde{y}\left(t\right)\Vert }^2+2{\tilde{y}}^{\text{T}}P{L}_1\tilde{e}\left(t\right)\\ \le -\left(\alpha {\lambda }_0-2l\Vert P\Vert \right){\displaystyle \underset{i=1}{\sum }{\tilde{y}}_i^2+}2{\displaystyle \underset{i=1}{\sum }{\displaystyle \underset{j\in N_i}{\sum }{\xi }_i{a}_{ij}{\tilde{y}}_i({\tilde{e}}_i\left(t\right)-{\tilde{e}}_j(\; t\; ))}}\end{array}$

根据引理2可以得到：

${\tilde{y}}_i{\tilde{e}}_i-{\tilde{y}}_i{\tilde{e}}_j\le \theta {\tilde{y}}_i^2+\frac{1}{2\theta }{\tilde{e}}_i^2+\frac{1}{2\theta }{\tilde{e}}_j^2$

因此可以对 $\stackrel{\dot{}}{V}$ 进行放缩：

$\begin{array}{c}\stackrel{\dot{}}{V}\le -\left(\alpha {\lambda }_0-2l\Vert P\Vert \right){\displaystyle \underset{i=1}{\sum }{\tilde{y}}_i^2}+2{\displaystyle \underset{i=1}{\sum }{\displaystyle \underset{j\in N_i}{\sum }{\xi }_i}}{a}_{ij}{\tilde{y}}_i\left({\tilde{e}}_i\left(t\right)-{\tilde{e}}_j\left(t\right)\right)\\ \le -\left(\alpha {\lambda }_0-2l\Vert P\Vert \right){\displaystyle \underset{i=1}{\sum }{\tilde{y}}_i^2}+2{\xi }_{\max }{\displaystyle \underset{i=1}{\sum }{\displaystyle \underset{j\in N_i}{\sum }{a}_{ij}\left(\theta {\tilde{y}}_i^2+\frac{1}{2\theta }{\tilde{e}}_i^2+\frac{1}{2\theta }{\tilde{e}}_j^2\right)}}\\ =-\left(\alpha {\lambda }_0-2l\Vert P\Vert \right){\displaystyle \underset{i=1}{\sum }{\tilde{y}}_i^2}+2{\xi }_{\max }{\displaystyle \underset{i=1}{\sum }{\Delta }_i\theta {\tilde{y}}_i^2}+2{\xi }_{\max }{\displaystyle \underset{i=1}{\sum }\frac{1}{2\theta }{\Delta }_i{\tilde{e}}_i^2}+2{\xi }_{\max }{\displaystyle \underset{i=1}{\sum }{\displaystyle \underset{j\in N_i}{\sum }\frac{1}{2\theta }{a}_{ij}{\tilde{e}}_j^2}}\\ =-{\displaystyle \underset{i=1}{\sum }\left(\alpha {\lambda }_0-2l\Vert P\Vert -2{\xi }_{\max }{\Delta }_i\theta \right){\tilde{y}}_i^2}+2{\xi }_{\max }{\displaystyle \underset{i=1}{\sum }\frac{1}{2\theta }{\Delta }_i{\tilde{e}}_i^2}+2{\xi }_{\max }{\displaystyle \underset{i=1}{\sum }\frac{1}{2\theta }{\Delta }_i{\tilde{e}}_j^2}\end{array}$

因为 ${\displaystyle \underset{i}{\sum }{\displaystyle \underset{j\in N_i}{\sum }\frac{1}{2\theta }{a}_{ij}{e}_j^2}}={\displaystyle \underset{i}{\sum }\frac{1}{2\theta }{\Delta }_i{e}_i^2}$，

所以可得： $\stackrel{\dot{}}{V}=-{\displaystyle \underset{i=1}{\sum }\left(\alpha {\lambda }_0-2l\Vert P\Vert -2{\xi }_{\max }{\Delta }_i\theta \right){\tilde{y}}_i^2}+2{\xi }_{\max }{\displaystyle \underset{i=1}{\sum }\frac{1}{\theta }{\Delta }_i{\tilde{e}}_i^2}$

所以根据式(19)可得： ${\tilde{e}}_i^2\le \frac{\theta {\sigma }_{i}K}{2{\Delta }_i{\xi }_{\max }}{\tilde{y}}_i^2$

所以可以得到：

$\stackrel{\dot{}}{V}\left(t\right)\le {\displaystyle \underset{i=1}{\sum }\left({\sigma }_i-1\right)K{\tilde{y}}_i^2}$ (20)

由上可见， $\stackrel{\dot{}}{V}\left(t\right)<0$，所以可以得到： $\underset{t\to +\infty }{\lim }\tilde{y}\left(t\right)=0$，从而使得系统(1)与系统(2)能够达到二分一致性跟踪控制。

定理4：针对跟随者系统(1)与领导者系统(2)，若限定事件触发函数(19)成立，则在控制协议(15)作用下，至少存在一个智能体q，使得该智能体任意两个连续事件触发时刻之间的时间间隔 $t_{k+1}^q-t_k^q$ 不小于：

$\tau =\frac{\alpha \theta {\sigma }_{i}K}{\left({\alpha }^2\Vert L_1\Vert +\alpha l\right)\left(\theta {\sigma }_{i}K-2\alpha N{\Delta }_i{\xi }_{\max }\right)}$

证明：令 $h=\arg \underset{i\in V}{\max }\left|{\tilde{y}}_i\right|$， $\left|{\tilde{e}}_i\right|\le \left|\tilde{e}\right|$ 对于所有的智能体都满足，则有： $\frac{\left|{\tilde{e}}_h\right|}{N\left|{\tilde{y}}_h\right|}\le \frac{\Vert \tilde{e}\Vert }{\Vert \tilde{y}\Vert }$。通过证明定理2的证明过程以及式子(19)可以解出：

$\tau =\frac{\alpha \theta {\sigma }_{i}K}{\left({\alpha }^2\Vert L_1\Vert +\alpha l\right)\left(\theta {\sigma }_{i}K-2\alpha N{\Delta }_i{\xi }_{\max }\right)}$

所以定理得证。

4. 数值仿真

考虑由5个智能体组成的非线性多智能体系统，其系统的通信拓扑结构设计如下：

Figure 1. Communication topology diagram

图1. 通信拓扑图

其中，节点0为领导者，节点1~4为跟随者。从图1可以看出领导者与智能1与智能体2之间为合作关系，智能体2与智能体3为对抗关系，智能体3和智能体4为合作关系，即： $V_1=\left\{0,1,2\right\}$， $V_2=\left\{3,4\right\}$。

根据该通信拓扑图，所以对应的Laplacian矩阵L为：

$L=\left[\begin{array}{cccc}2& -2& 0& 0\\ 0& 3& 3& 0\\ 0& 0& 6& -6\\ 0& 0& 0& 0\end{array}\right]$

在系统中 $f\left(x_i\left(t\right),t\right)=\sin \left(x_i\right)$，初始状态 $x_1\left(0\right)=2$， $x_2\left(0\right)=-1$， $x_3\left(0\right)=3$， $x_4\left(0\right)=-2$。领导者 ${\stackrel{\dot{}}{x}}_0=\sin \left(x_0\right)$，初值为5。

在集中式事件触发机制(14)下，参数设置为： $l=1$， $\alpha =3$， $\sigma =0.3$。图2给出了系统(1)与系统(2)在该机制下的状态轨迹：

Figure 2. Results of binary consistency tracking control of multi-agent system triggered by centralized events

图2. 集中式事件触发的多智能体系统二分一致性跟踪控制结果

从图2中可以看出，在集中式事件触发机制下智能体之间达到了二分一致性跟踪目标，智能体1与智能体2收敛到与领导者相同的状态，智能体3与智能体4收敛到与领导者模相等，符号相反的状态。

在分布式事件触发机制(26)下，设置参数为： $l=1$， $\alpha =6$， ${\sigma }_1=0.8$， ${\sigma }_2=0.9$， ${\sigma }_3=0.6$， ${\sigma }_4=0.7$。图3给出了系统(1)与系统(2)在该机制下的运动轨迹：

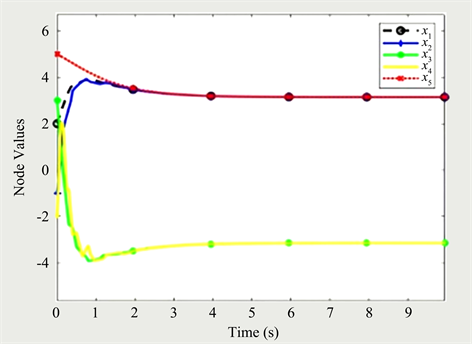
Figure 3. Results of binary consistency tracking control of multi-agent system triggered by distributed events

图3. 分布式事件触发的多智能体系统二分一致性跟踪控制结果

从图3中可以看出，在分布式事件触发机制下智能体之间达到了二分一致性跟踪目标，智能体1与智能体2收敛到与领导者相同的状态，智能体3与智能体4收敛到与领导者模相等，符号相反的状态。

5. 结论

本文研究了非线性多智能体系统的二分一致性跟踪控制问题，为解决传统时间采用控制造成的资源浪费问题，基于事件触发控制策略，设计了分布式和集中式控制协议。通过理论分析得出了所给的控制协议能够解决二分一致性跟踪控制问题。数值仿真结果验证了理论分析的正确性。

基金项目

重庆市自然科学基金(cstc2019jcyj-msxmX0491)；重庆市教委科技项目青年项目(KJQN201901145)。

NOTES

^*第一作者。

^#通讯作者。