1. 引言
我国经济持续增长,基础设施建设日益完善,人们越来越追求交通的便利与快捷,高速公路和高铁的建设正在飞速发展,隧道工程作为基础建设中的重要组成部分,也离不开各方面的研究 [1]。
隧道的开挖不可避免的会改变土体的原始形态,在隧道开挖过程中引起土体的扰动,从而引起土体的变形,改变土体的应力分布,并导致隧道周围塑性区的变化以及隧道周围地表的沉降 [2]。在双马蹄形隧道工程施工过程中,两条隧道是相互独立且相互联系的,双马蹄形隧道在施工过程中难度高于普通双线独立隧道。隧道开挖前后准确的确定土体的应力状态和塑性区域,将为隧道的开挖过程及支护等提供必要的理论支撑 [3]。
近年来大量国内学者外在隧道开挖数值研究方面,进行了大量研究工作。华薇 [4] 等通过有限元模型的计算分析得到隧洞的每次开挖,其周围都会产生变形,以及每次开挖后,隧洞受到的应力将会重新分布,通过支护围岩的方法,缓解了应力集中的问题,大大提高了隧洞侧壁的支撑强度。通过有限元进行隧洞灌浆压力模拟分析,给出3个方案,认为其中一个方案最为可行,仅在隧洞顶拱和底板的中点区域产生拉应力,其它的部位为压应力,竖向应力仅在隧洞顶拱中点及顶拱另外的转折点处出现拉应力且值很小,其它部位为压应力值。
本文通过有限元软件COMSOL建立双马蹄形隧道开挖模型,并分析计算出应力分布状况、安全塑性区域以及地表沉降量,为实际隧道的开挖提供了参考。
2. 有限元模拟
2.1. 模型建立
在实际工程中,隧道开挖是分两步进行的,本文利用有限元软件COMSOL也是分两步进行模拟分析的。首先在第一个研究中,计算了隧道开挖前土壤的应力状态。然后在第二项研究中,计算了土壤被去除后的弹塑性行为。这需要结合在第一个研究中计算的应力反应。利用线性弹性材料模型中的活化特征来模拟土壤去除情况。为了加快计算速度,第一步考虑土壤为弹性,有现场通过测量和计算就可以确定初始地应力的值,第二步加入Drucker-Prager (Drucker-Prager模型,简称DP模型,该模型对MC模型的屈服面函数作了适当的修改并且考虑了体积力对屈服的影响,易于程序的编制和进行数值计算,可用于颗粒状的材料,例如:土壤、岩石、混凝土等)土壤塑性模型。在二维平面应变下求解了该例子。最后再将仿真计算出来的结果与开挖前土体的状态进行对比分析 [5]。
本隧道开挖模型采用二维建模,采用平面问题的求解方法。在自由岩土体中挖出两条平行马蹄形隧道,土体高40 m,宽90 m,第一个隧道正方形截面中心距土体下端15 m,距土体左端35 m,第二个隧道正方形截面中心距土体下端15 m,距土体左端55 m,正方形截面的边长均为10 m,两隧道的间距为10 m。第一个隧道半圆形截面圆心距土体下端20 m,距土体左端35 m,第二个隧道半圆形截面中心距土体下端20 m,距土体左端55 m,半圆形截面的半径均为5 m。线弹性材料为各向同性,土体力学参数分别为杨氏模量取12e6 Pa,泊松比为0.495,密度为2000 kg/m3,内聚力为130 kPa,内摩擦角为30˚。土体的下边界设置为固定约束,土体的左右边界设置为辊支承,隧道开挖后的作业面和上边界均为自由边界 [6]。建立模型如图1所示。
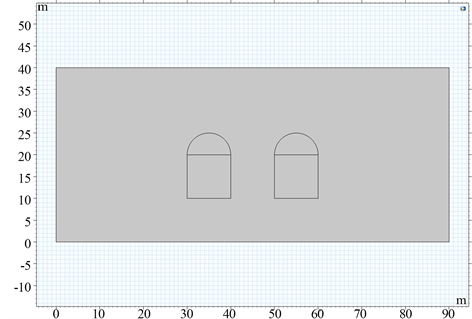
Figure 1. Establishment of double horseshoe tunnel excavation model
图1. 双马蹄形隧道开挖模型建立
2.2. 网格划分
COMSOL软件提供了便捷的网格划分工具,本文通过软件自动生成网格单元。采用自动生成网格,计算结果准确、精度高。由于计算机储存功能较大和计算量要求较高,在利用COMSOL软件操作时采用比较多的三角网格和一些节点数的个数 [7]。如图2所示,靠近隧道半圆形边界的网格很密集,尤其是在隧道的上部,而在其余区域网格较稀疏。

Figure 2. Mesh generation of double horseshoe tunnel
图2. 双马蹄形隧道的网格划分
2.3. 稳态计算
岩土体的单元实验模拟分析就是为了尽可能还原真实的隧道开挖现场,所以模型的稳态计算主要分为两个部分 [8]。第一部分先计算隧道开挖前的应力状态,一般情况下以自然状态的岩土体初始应力值作为岩土体的应力状态;第二部分进行隧道开挖后的应力状态以及等效塑性应变计算,以第一部分计算得到的应力值作为岩土体此时的外部应力进行计算 [9]。
3. 计算结果及分析
开挖前后土体的应力分布图如图3和图4所示。开挖前的最大初始应力为14 kPa,出现在土体的最下侧。开挖后,土体中隧道周边的应力较大,最大应力发生在两个隧道的下边角位置,为90 kPa。
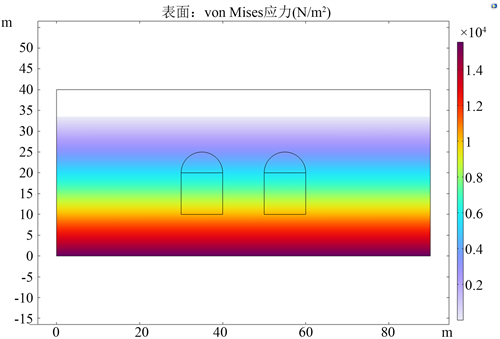
Figure 3. Stress distribution diagram of soil before excavation
图3. 土体开挖前应力分布图
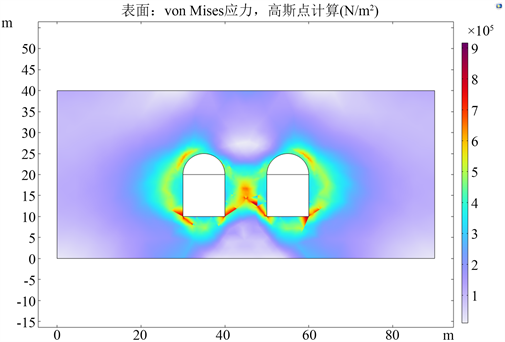
Figure 4. Stress distribution diagram of soil after excavation
图4. 土体开挖后应力分布图
本文还研究了隧道间距对隧道开挖后的应力状态的影响,如图4和图5所示。当两个隧道的间距比较大时,最大应力为90 kPa,出现在隧道的底角位置,此时隧道周边的应力与底角位置的应力相差较大,为30 kPa,这主要是因为当隧道间距较大时,两个隧道相当于是独立的个体,而隧道的底角是直角,容易引起应力集中,所以此时隧道底角处应力最大;但当两个隧道的间距减小到一定程度时,隧道周边的应力整体小幅度增加,可底角处的应力大幅减小,此时的最大应力仅有70 kPa,且分布较为均匀,这主要是因为当隧道间距减小到一定程度时,两隧道渐渐被视为一个整体,各自所受到的应力相互影响,从而使两隧道周边的应力小幅提升,底角的应力大幅减小,这是由于底角处的应力被周围分担了。

Figure 5. Stress distribution diagram when tunnel spacing is too small
图5. 隧道间距过小时的应力分布图
隧道开挖中的塑性区直接影响施工中隧道的支护方案,因此塑性区的形状和大小至关重要 [10]。图6显示的是隧道正常间距时开挖后的塑性区,此时最大的塑性应变区域出现在两隧道内侧的底角位置,最大塑性应变为0.3,这主要是因为当隧道间距较大时,两个隧道相当于是独立的个体,隧道之间的土体同时受到两隧道的影响,底角又是应力集中部位,所以导致隧道内侧底角位置塑性应变最大;图7显示的是隧道间距过小时开挖后的塑性区,可以明显看出此时的塑性变形比隧道正常间距开挖后的塑性变形更加严重,此时最大的塑性应变区域出现在两个隧道之间的中心点及内侧底角位置,最大塑性应变为0.39,这主要是因为当隧道间距减小到一定程度时,隧道之间的土体受到两隧道的影响增加,不但最大塑性应变变大,最大塑性应变区域也由隧道内侧底角位置延伸到隧道间土体中心区域。由此可知,两隧道之间的间距不应过小,否则塑性应变会大幅增加。
地表的沉降对地面建筑设施的安全有着很大的影响,所以隧道开挖模拟是非常重要的 [9]。地表的沉降如图8和图9所示。图8和图9的横坐标表示地表上从土体左端开始的坐标,纵坐标表示地表沉降值。可以看到,最大沉降位移发生在两个隧道各自的中线位置,当隧道间距逐渐减小时,两隧道之间的土体沉降量也随之增大,这是因为随着间距减小,两隧道渐渐被视为一个整体,这也佐证了上面的分析。
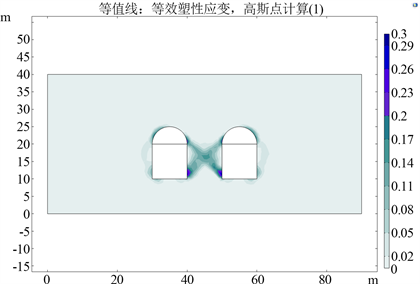
Figure 6. Equivalent plastic strain diagram after excavation at normal spacing
图6. 正常间距时开挖后的等效塑性应变图
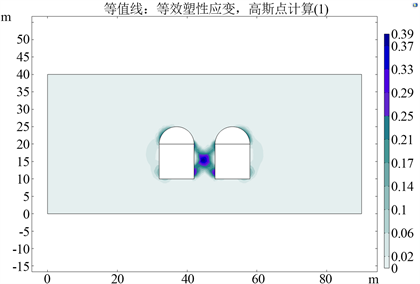
Figure 7. Equivalent plastic strain diagram after excavation when the spacing is too small
图7. 间距过小时开挖后的等效塑性应变图
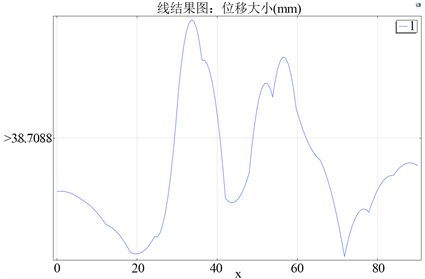
Figure 8. Surface settlement curve after excavation at normal spacing
图8. 正常间距时开挖后的地表沉降曲线
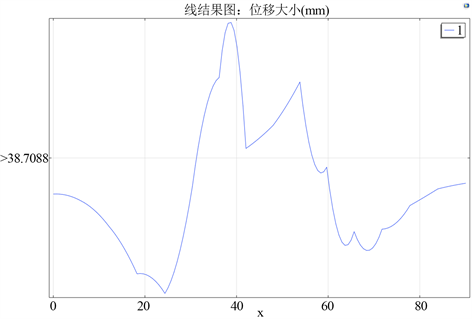
Figure 9. Surface settlement curve after excavation when the spacing is too small
图9. 间距过小时开挖后的地表沉降曲线
4. 结论
经过研究各种隧道开挖的理论和方法,决定采用有限元软件COMSOL对双马蹄形隧道开挖进行仿真计算。应用Drucker-Prager本构模型对隧道开挖问题进行弹塑性力学分析。本文给出了采用COMSOL软件进行仿真平行双马蹄形隧道开挖的原理和过程,模拟了自由土体中隧道开挖时的土体应力分布、塑性区位置和地表沉降。给出了应力分布图、等效塑性应变图和地表沉降曲线。得出的主要结论为:
在自由土体中开挖双马蹄形隧道后,正常间距时,两个隧道的底角位置应力最大,最大应力为90 kPa,塑性应变也是隧道内侧的底角位置较大,最大塑性应变为0.3;但当两个隧道的间距缩小到一定程度时,隧道周边的应力会小幅增大,可隧道底角位置的应力会大幅减小,此时的最大应力仅有70 kPa,且分布较为均匀,塑性应变最大的区域出现在两个隧道之间的中心点及内侧底角位置,此时的最大塑性应变为0.39;最大沉降位移发生在两个隧道各自的中线位置。
NOTES
*通讯作者。