双曲空间上具有组合非线性项的半线性热方程Fujita指标的一个注记

A Note on the Fujita Exponent of a Semilinear Heat Equation with Combined Nonlinearities on the Hyperbolic Space

摘要: 本文研究了在Hⁿ上带有时间加权函数的半线性热方程的Fujita指标。文章将时间加权项的研究从两项扩展到了k重组合非线性项，并通过比较定理，对方程的Fujita指标给出了一个简单而统一的证明。

Abstract: In this short note, we study the Fujita exponent for a time-weighted semilinear heat equation on Hⁿ. The results of this paper extend the time-weighted functions from two to k-multiple combined nonlinearities. We give a simple and unified proof for the Fujita exponent by the comparison theorem.

1. 引言

本文考虑带有时间加权项的半线性热方程

$\{\begin{array}{ll}{u}_t={\Delta }_{{ℍ}^n}u+{\displaystyle \underset{i=1}{\overset{k}{\sum }}{\text{e}}^{{\alpha }_{i}t}}{u}^{p_i},\hfill & \left(x,t\right)\in {ℍ}^n\times \left(0,T\right),\hfill \\ u\left(x,0\right)=u_0\left(x\right),\hfill & x\in {ℍ}^n,\hfill \end{array}$ (1-1)

其中 ${ℍ}^n$ 是n维双曲空间， ${\Delta }_{{ℍ}^n}$ 是 ${ℍ}^n$ 上的拉普拉斯–贝尔特拉米算子， $k\ge 2$， ${\alpha }_i>0$， $p_i>1$， $u_0\left(x\right)$ 是 $C\left({ℍ}^n\right)\cap L^{\infty }\left({ℍ}^n\right)$ 上的正函数。

在1966年，Fujita [1] 考虑了半线性热方程的Cauchy问题

$\{\begin{array}{ll}{u}_t=\Delta u+u^p,\hfill & \left(x,t\right)\in {ℝ}^N\times \left(0,T\right),\hfill \\ u\left(x,0\right)=u_0\left(x\right)\ge 0,\hfill & x\in {ℝ}^N.\hfill \end{array}$ (1-2)

他证明了存在临界指标 $p^{\ast }=1+2/n$ ：如果 $1<p<p^{\ast }$，则方程(1-2)不存在全局正解；如果 $p>p^{\ast }$，当初值 $u_0$ 足够小时，方程(1-2)存在全局正解。对于临界情况 $p=p^{\ast }$，方程的所有正解都会在有限时间爆破(详见 [2] [3] [4] [5])。这一类研究临界指标的问题被称为Fujita问题。在Fujita的论文以后，很多人去关注Fujita型的方程，也得到了很多有意思的结果(参看 [6] [7] [8] [9] [10] 和它们的参考文献)。半个世纪以来，Fujita型方程的研究已经形成了一个庞大的理论体系。

特别地，对于 ${ℝ}^n$ 上的有界域，Meier [11] 考虑了初边值问题

$\{\begin{array}{ll}{u}_t=\Delta u+{\text{e}}^{\alpha t}{u}^p,\hfill & \left(x,t\right)\in D\times \left(0,T\right),\hfill \\ \begin{array}{l}u\left(x,0\right)=u_0\left(x\right)\ge 0,\\ u\left(x,t\right)=0,\end{array}\hfill & \begin{array}{l}x\in D,\\ \left(x,t\right)\in \partial D\times \left(0,T\right)\end{array}\hfill \end{array}$ (1-3)

其中D是 ${ℝ}^n$ 上的有界域， $\alpha >0$ 和 $p>1$。他证明了方程(1-3)的临界指标是 $p_{\alpha }^{\ast }=1+\alpha /\lambda$，其中 $\lambda$ 是D上具有Dirichlet边界的 $-\Delta$ 的第一特征值。而后，Wang和Yin [12] 证明了该临界指标本身是属于爆破情况。

Fujita指标问题不仅在欧氏空间上取得很多的成果，它也有很多在非欧氏空间上的研究成果。在文献 [13] 中，Bandle、Pozio和Tesei在双曲空间中得到了一类Fujita型结果。他们研究了方程(1-1)当 $k=1$ 时的情况。他们获得了以下结果

定理1 ( [13]，定理1.1)设 $p_{{\alpha }_1}=1+{\alpha }_1/{\lambda }_0$，其中 ${\lambda }_0={\left(n-1\right)}^2/4$ 是 $-{\Delta }_{{ℍ}^n}$ 的 $L_2$ 谱的下确界。则

1) 如果 $1<p_1<p_{{\alpha }_1}$，方程的每个非平凡非负解在有限时间内爆破；

2) 如果 $p>p_{{\alpha }_1}$，对于小的初始数据，问题具有全局正解；

3) 如果 $p_1=p_{{\alpha }_1}$， ${\alpha }_1>2/3{\lambda }_0$，则方程存在全局正解。

而对于临界情况 $p_1=p_{{\alpha }_1}$， $0<{\alpha }_1\le 2/3{\lambda }_0$，Wang和Yin [12] 在2014年证明了该指标也是存在全局正解的。 [12] 和 [13] 的结果表明双曲空间上的临界指标和欧氏空间上的临界指标解的情况是不一样的。在有界域上临界指标本身是属于爆破情形，而在双曲空间上解却是全局存在的。

Wu [14] 将 [13] 的结果将一个时间加权项拓展到两个时间加权 ${\text{e}}^{\alpha t}{u}^p+{\text{e}}^{\beta t}{u}^q$，即考虑了方程(1-1)当 $k=2$ 的情况。设 $p_{{\alpha }_1}=1+{\alpha }_1/{\lambda }_0$ 和 $p_{{\alpha }_2}=1+{\alpha }_2/{\lambda }_0$。她证明了如果 $1<p_1<p_{{\alpha }_1}$ 或 $1<p_2<p_{{\alpha }_2}$，方程的非负解会在有限时间爆破；如果 $p_1>p_{{\alpha }_1}$ 且 $p_2>p_{{\alpha }_2}$，则方程存在非负全局解。对于临界情况，如果 $p_1=p_{{\alpha }_1}$ 且 $p_2=p_{{\alpha }_2}$，方程存在正的全局解。而对于剩下的临界指标 $\left\{\left(p,q\right)|p=p_{\alpha },q>q_{\beta }\right\}\cup \left\{\left(p,q\right)|p>p_{\alpha },q=q_{\beta }\right\}$ (下图1实线部分)还是一个开放的问题。

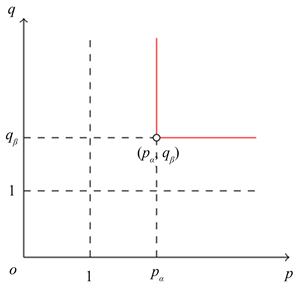
Figure 1. Critical exponents of the equation

图1. 方程的临界指标

在 [14]，对于爆破部分，文章采用了 [13] 中导出矛盾的方法。对于全局存在解的证明分为三部分：1)

如果 $1<p_1<p_{{\alpha }_1}$ 或 $1<p_2<p_{{\alpha }_2}$，构造了一个全局上解 $\bar{u}={\text{e}}^{-{\lambda }_{0}t}\xi \left(x\right)\psi \left(x\right)$，其中 $\psi \left(x\right)$ 是 ${ℍ}^n$ 上的第一特征值；2) 如果 $\left(p_1,p_2\right)=\left(p_{{\alpha }_1},p_{{\alpha }_2}\right)$，且 ${\alpha }_1\ge {\alpha }_2>2/3{\lambda }_0$ 或 ${\alpha }_2\ge {\alpha }_1>2/3{\lambda }_0$，构造了一个全局上解 $\bar{u}=\zeta \left(t\right)g_n\left(x,0,t+t_0\right)$，其中 $g_n\left(x,y,t\right)$ 是双曲空间上的热核；3) 如果 $\left(p_1,p_2\right)=\left(p_{{\alpha }_1},p_{{\alpha }_2}\right)$，且a) ${\alpha }_1\ge {\alpha }_2$， $0<{\alpha }_2\le 2/3{\lambda }_0$ 或b) ${\alpha }_2\ge {\alpha }_1$， $0<{\alpha }_1\le 2/3{\lambda }_0$，则构造了一个非线性全局上解 $\bar{u}={\text{e}}^{-{\lambda }_{0}t}\bar{\xi }\left(x\right)$。

在本文中，我们的结果包括了 [14] 的结论，并补充了 [14] 中未证明的情形。对于爆破部分，本文采用了相对简单的证明方法。对于全局存在部分，我们给出了一个统一的证明。

以下是本文的主要结果。

定理2 设 $p_{{\alpha }_i}=1+{\alpha }_i/{\lambda }_0$，( $i=1,\cdots ,k$ )。假设初值 $u_0\ge 0$ 和 $u_0\in C\left({ℍ}^n\right)\cap L^{\infty }\left({ℍ}^n\right)$。则

1) 如果存在 $i\in \left\{1,\cdots ,k\right\}$，使得 $1<p_i<p_{{\alpha }_i}$，则方程(1-1)的每个非平凡非负解都会在有限时间爆破；

2) 如果对任意 $i=1,\cdots ,k$ 有 $p_i\ge p_{{\alpha }_i}$，则方程(1-1)对小初值有正的全局解。

对于定理2(1)，我们将构造问题(1-1)的爆破下解 $\underset{\_}{u}$。对于定理2(2)，我们将对 [12] 中的Wang和Yin的所采用的证明方法进行修正，以证明定理，即将问题(1-1)转化为一个无时间t的抛物型方程。证明的思想是利用非线性椭圆方程正解的存在性构造一个正的上解。

论文的结构如下：在第2节中，我们将介绍双曲空间 ${ℍ}^n$ 的一些基本性质，证明问题(1-1)解的存在唯一性，以及引入证明定理2所需要的一个引理。在第3节中，我们将证明本文的结果。

2. 准备工作

首先，我们在本章节引入双曲空间的一些基本性质。设 $B_r=\left\{x\in {ℝ}^n:\left|x\right|<r\right\}$，则双曲空间 ${ℍ}^n$ 等价于赋予庞加莱度量的 $B_1$

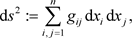
其中

$g_{ij}:={\left(\frac{2}{1-{\left|x\right|}^2}\right)}^2{\delta }_{ij}\left(i,j=1,\cdots ,n\right).$

用 $\text{d}\mu$ 表示双曲体积，它可以表示为

对于任意固定点 $o\in {ℍ}^n$ 和 $x\in {ℍ}^n$，考虑测地距离

$\rho \left(x\right)={\displaystyle {\int }_0^{\left|x\right|}\frac{2}{1-s^2}\text{d}s}=\log \left(\frac{1+\left|x\right|}{1-\left|x\right|}\right),$

因此有

$\left|x\right|=\tanh \frac{\rho }{2},\frac{2}{1-{\left|x\right|}^2}=2{\left(\cosh \frac{\rho }{2}\right)}^2.$

在 ${ℍ}^n$ 上的函数 $u\in C^2\left({ℍ}^n\right)$ 的拉普拉斯-贝尔特拉米算子可以表示为

${\Delta }_{{ℍ}^n}u=\frac{1}{4}{\left(1-{\left|x\right|}^2\right)}^2{\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{{\partial }^{2}u}{\partial x_i^2}}+\frac{n-2}{2}\left(1-{\left|x\right|}^2\right){\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\frac{\partial u}{\partial x_i},$

和

${\Delta }_{{ℍ}^n}u=\frac{{\partial }^{2}u}{\partial {\rho }^2}+\left(n-1\right)\coth \rho \frac{\partial u}{\partial \rho }+\frac{1}{{\left(\sinh \rho \right)}^2}{\Delta }_{\theta }u,$

其中 ${\Delta }_{\theta }$ 是 ${ℝ}^n$ 的 $n-1$ 维球面上的拉普拉斯-贝尔特拉米算子。关于双曲空间的更多性质，可以查看 [13] 和 [15]。

接下来，我们引入弱解的概念以及问题(1-1)解的存在唯一性。对于任何 $T>0$，设 ${\Omega }_T={ℍ}^n\times \left(0,T\right]$。

定义1 假设 $u_0\left(x\right)\in C\left({ℍ}^n\right)\cap L^{\infty }\left({ℍ}^n\right)$ 和 $u_0\ge 0$。如果函数 $u\in C\left({\bar{\Omega }}_T\right)$ 满足下列条件，则称函数u为问

题(1-1)的弱解

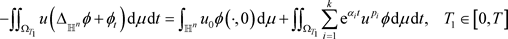
其中 $\varphi \in C^{2,1}\left({\bar{\Omega }}_{T_1}\right)$ 是一个任意函数，且使得对任意的 $t\in \left[0,T_1\right)$， $\text{supp}\varphi \left(\cdot ,t\right)⋐{ℍ}^n$ 和 $\varphi \left(\cdot ,T_1\right)=0$。

命题1 设 $u_0\left(x\right)\in C\left({ℍ}^n\right)\cap L^{\infty }\left({ℍ}^n\right)$ 且 $u_0\ge 0$。则存在 $T>0$ 使得问题有唯一的弱解 $u\in L^{\infty }\left({\Omega }_T\right)$。

对 $k=1$ 和 $k=\text{2}$ 的情形，在( [13]，定理3.1)和( [14]，定理2.3)已经证明命题1是正确的。而对于更一般的k，也可以用类似的方法加以证明。在这里，我们省略这一部分证明细节。

最后，我们介绍了Mancini和Sandeep关于双曲空间中非线性椭圆型方程正解存在性的一个结果。

引理1 ( [16]，定理1.3)设 $p>1$，如果 $n=2$ 且 $1<p<\left(n+2\right)/\left(n-2\right)$，或者 $n\ge 3$，则方程

${\Delta }_{{ℍ}^n}v+\lambda v+v^p=0$

对任意的 $\lambda \le {\left(n-1\right)}^2/4$ 都有一个正解，且满足

${\left|v\right|}_{\lambda }:={\left[{\displaystyle {\int }_{{ℍ}^n}\left({\left|{\nabla }_{{ℍ}^n}v\right|}^2-\lambda v^2\right)\text{d}\mu }\right]}^{\frac{1}{2}}<\infty .$

3. 定理证明

证明定理2(1)。

假设存在 $i\in \left\{1,\cdots ,k\right\}$ 使得 $1<p_i<p_{{\alpha }_i}$。设 $\underset{\_}{u}$ 是下列方程的解

$\{\begin{array}{ll}{u}_t={\Delta }_{{ℍ}^n}u+{\text{e}}^{{\alpha }_{i}t}{u}^{p_i},\hfill & \left(x,t\right)\in {ℍ}^n\times \left(0,T\right),\hfill \\ u\left(x,0\right)=u_0\left(x\right)\ge 0,\hfill & x\in {ℍ}^n.\hfill \end{array}$

显然， $\underset{\_}{u}$ 是问题的下解。由定理1(1)， $\underset{\_}{u}$ 会在有限时间爆破。通过比较定理，问题(1-1)的解也会在有限时间爆破，定理2(1)证明完毕。

证明定理2(2)。

通过直接计算，如果 $\bar{v}\left(x\right)$ 满足下列不等式，则 $\bar{u}\left(x,t\right)={\text{e}}^{-{\lambda }_{0}t}\bar{v}\left(x\right)$ 是问题(1-1)的上解

${\Delta }_{{ℍ}^n}\bar{v}+{\lambda }_0\bar{v}+{\displaystyle \underset{i=1}{\overset{k}{\sum }}{\text{e}}^{\left({\alpha }_i+{\lambda }_0\left(1-p_i\right)\right)t}{\bar{v}}^{p_i}}\le 0.$ (3-1)

接下来，我们的目标是找到一个函数 $\bar{v}\left(x\right)$ 满足(3-1)。

因为 $p_i\ge p_{{\alpha }_i}$，( $i=1,\cdots ,k$ )，可以得到

${\alpha }_i+{\lambda }_0\left(1-p_i\right)\le {\alpha }_i+{\lambda }_0\left(1-p_{{\alpha }_i}\right)={\alpha }_i+{\lambda }_0\left(1-\left(1+{\alpha }_i/{\lambda }_0\right)\right)=0.$

则

${\text{e}}^{\left({\alpha }_i+{\lambda }_0\left(1-p_i\right)\right)t}\le 1,i=1,\cdots ,k.$ (3-2)

取 $q\in \left(1,\underset{1\le i\le k}{\min }\left\{p_i,\left(n+2\right)/\left(n-2\right)\right\}\right)$。

显然，如果 $n=2$，则 $q<\infty$ ；如果 $n>2$，则 $q<\left(n+2\right)/\left(n-2\right)$。所以q满足引理2.1的条件，并且下列非线性椭圆方程

${\Delta }_{{ℍ}^n}v+{\lambda }_{0}v+v^q=0,$ (3-3)

存在正解 $v\left(x\right)$。

设

$v_{\eta }\left(x\right)=\frac{1}{\eta }v\left(x\right),$

其中 $\eta =\max \left\{k^{1/\left(q-1\right)},{\Vert v\Vert }_{L^{\infty }\left({ℍ}^n\right)}\right\}$，则 ${\Vert v_{\eta }\Vert }_{L^{\infty }\left({ℍ}^n\right)}\le 1$。因为 $q<\underset{1\le i\le k}{\min }\left\{p_i,\left(n+2\right)/\left(n-2\right)\right\}$，可以得到 $p_i>q$ 和 $v_{\eta }^{p_i}\le v_{\eta }^q$，结合(3-2)和(3-3)，则有

$\begin{array}{c}{\Delta }_{{ℍ}^n}{v}_{\eta }+{\lambda }_0{v}_{\eta }+{\displaystyle \underset{i=1}{\overset{k}{\sum }}{\text{e}}^{\left({\alpha }_i+{\lambda }_0\left(1-p_i\right)\right)t}}{v}_{\eta }^{p_i}\le {\Delta }_{{ℍ}^n}{v}_{\eta }+{\lambda }_0{v}_{\eta }+{\displaystyle \underset{i=1}{\overset{k}{\sum }}{v}_{\eta }^{p_i}}\\ \le \frac{1}{\eta }{\Delta }_{{ℍ}^n}v+\frac{1}{\eta }{\lambda }_{0}v+k{v}_{\eta }^q\\ =\frac{1}{\eta }{\Delta }_{{ℍ}^n}v+\frac{1}{\eta }{\lambda }_{0}v+\frac{k}{{\eta }^{q-1}}\frac{1}{\eta }{v}^q\\ \le \frac{1}{\eta }\left({\Delta }_{{ℍ}^n}v+{\lambda }_{0}v+v^q\right)\\ =0.\end{array}$

因此， $\bar{v}\left(x\right)=v_{\eta }\left(x\right)$ 满足条件(3-1)。所以，对于所有的 $i\in \left\{1,\cdots ,k\right\}$，如果 $p_i\ge p_{{\alpha }_i}$，问题(1-1)会有一个上解。通过比较原理，对于初值 $0\le u_0\left(x\right)\le v_{\eta }\left(x\right)$，问题(1-1)会有一个正的全局解。证明完毕。