1. 引言
有限状态分布检验有三个常用方法。第一个是Х2拟合优度检验方法 [1] [2] [3] 。设一总体有K个状态,其中第i个状态出现的概率为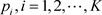 。对总体进行m次重复抽样,其中第i个状态出现得
。对总体进行m次重复抽样,其中第i个状态出现得 次。由皮尔孙(Pearson)定理,拟合优度检验的Х2统计量的极限分布为自由度为
次。由皮尔孙(Pearson)定理,拟合优度检验的Х2统计量的极限分布为自由度为 的卡方分布,其中q为原总体分布要估计的参数个数。
的卡方分布,其中q为原总体分布要估计的参数个数。
 (1.1)
(1.1)
记有限状态分布的假设检验为
 (1.2)
(1.2)
给定显著水平 ,根据皮尔孙定理(1.1),当m充分大时,Х2拟合优度检验为
,根据皮尔孙定理(1.1),当m充分大时,Х2拟合优度检验为
 (1.3)
(1.3)
作为一个特例,当总体只有两个状态时,其分布检验就是二项检验(binomial test)。二项检验既可以用Х2拟合优度检验方法,也可以用二项分布进行精确分布检验 [4] [5] [6] 。对总体进行m次独立抽样,其中状态1和状态2分别抽得 次和
次和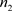 次,抽样分布为
次,抽样分布为
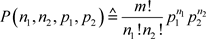 (1.4)
(1.4)
记假设检验为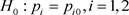 ,
,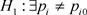 。在这个假设条件下,给定显著水平
。在这个假设条件下,给定显著水平 ,检验公式为
,检验公式为
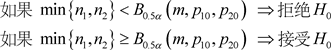 (1.5)
(1.5)
其中 为
为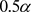 分位数。
分位数。
有限状态分布检验的另一个常用方法是利用似然比检验方法 [3] [7] 。在大样本的条件下,似然比可以表示为Х2统计量。
 (1.6)
(1.6)
在假设检验(1.2)的条件下,给定显著水平 ,根据皮尔孙定理(1.1),当m充分大时,Х2拟合优度检验为
,根据皮尔孙定理(1.1),当m充分大时,Х2拟合优度检验为
 (1.7)
(1.7)
过去,由于计算机和程序都比较落后,在不能找到精确分布时,我们只能借助极限分布处理假设检验问题。但这种方法有两个问题。首先,由于真实分布构造的拒绝域被用极限分布所构造的拒绝域替代。而这两种拒绝域的差异并不能在假设检验中表现出来。因此,用极限分布构造的假设检验含有无法评估的分布误差。我们只能寄希望于样本量足够大,两种分布误差足够小,使拒绝域的差异可以忽略不计。
其次,本文提出的带判别函数的方法可以有各种不同的判别函数。即使检验有极限分布,其极限分布也可能有不同的形式。我们只能逐个判别函数进行讨论。如果用精确分布的话,就是多项分布,与判别函数无关。现在,由于计算机的发展,用精确分布处理假设检验变得越来越可行,特别在抽样个数不是很大的时候。
本文第二节将介绍有限状态分布检验的一种带判别函数检验方法。第三节将说明几种传统的检验方法,例如二项分布检验方法,Х2拟合优度检验和似然比检验方法都是带判别函数检验方法的特例。最后,本文比较几种判别函数检验方法的检验效率。
2. 一种检验方法
设一总体有K个状态,其中第i个状态出现的概率为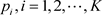 。记
。记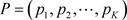 。对总体进行m次重复抽样,其中第i个状态出现得
。对总体进行m次重复抽样,其中第i个状态出现得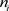 次。样本空间Ω由如下的K维向量构成,
次。样本空间Ω由如下的K维向量构成, ,其中
,其中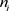 为非负整数,且
为非负整数,且 。样本空间Ω服从K项分布
。样本空间Ω服从K项分布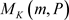 ,样本点N的概率为 [8]
,样本点N的概率为 [8]
 (2.1)
(2.1)
现对总体的分布进行假设检验(1.2)。记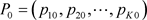 。对总体进行m次重复抽样,记抽到的样本为
。对总体进行m次重复抽样,记抽到的样本为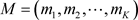 。记假设检验的判别函数为:
。记假设检验的判别函数为:
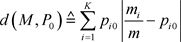 (2.2)
(2.2)
判别函数是样本的分布频率与目标概率的平均距离。在零假设成立的条件下,样本空间为服从K项分布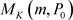 。记
。记
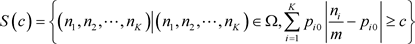 (2.3)
(2.3)
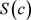 为在样本空间中,分布频率与假设概率平均距离大于等于c的点组成的集合。
为在样本空间中,分布频率与假设概率平均距离大于等于c的点组成的集合。
在零假设成立的条件下,样本的分布频率应该与假设概率相差不大。如果样本的分布频率与概率相差较大,那说明抽样出现不正常的情况。因此,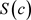 是由异常样本构成的集合。如果异常点集合的概率很小,它就是拒绝域。其思路是,如果样本落在拒绝域上,它表明异常的小概率事件发生,统计学上的“反例”出现,推翻了原假设。
是由异常样本构成的集合。如果异常点集合的概率很小,它就是拒绝域。其思路是,如果样本落在拒绝域上,它表明异常的小概率事件发生,统计学上的“反例”出现,推翻了原假设。
给定显著水平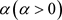 ,假设检验的拒绝域定义为
,假设检验的拒绝域定义为
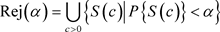 (2.4)
(2.4)
简单地说,拒绝域就是在 中概率小于
中概率小于 的最大集合,而接受域就是
的最大集合,而接受域就是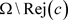 。
。
在检验中,我们可以通过计算检验的概率值p来判断零假设是否被拒绝。根据检验的定义,概率值表达如下,
 (2.5)
(2.5)
它是由满足某个条件的样本构成的集合的概率,这个条件是样本的分布频率与目标概率的平均距离大于等于抽到的样本的分布频率与目标概率的平均距离。
如果概率值p小于显著水平 ,我们就拒绝零假设;否则我们就接受(不拒绝)零假设。这个结论的证明很简单。从(1.6)可知,如果概率值p小于显著水平
,我们就拒绝零假设;否则我们就接受(不拒绝)零假设。这个结论的证明很简单。从(1.6)可知,如果概率值p小于显著水平 ,说明抽到的样本落在拒绝域里,因此拒绝零假设。如果概率值p大于等于显著水平
,说明抽到的样本落在拒绝域里,因此拒绝零假设。如果概率值p大于等于显著水平 ,说明抽到的样本落在接受域里,因此接受零假设。
,说明抽到的样本落在接受域里,因此接受零假设。
在重复抽样个数不是很大的时候,上述概率值可利用精确分布(K项分布)计算。
例1:设一色子在随机抛掷中每个数字朝上的概率相等。现随机抛掷100次,数字1到数字6朝上的频数分别为 。给定显著水平
。给定显著水平 ,进行检验假设:
,进行检验假设:
 ,
,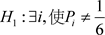 。
。
解法1:根据公式(1.6)计算检验的概率值,记抽样频率与目标概率的平均距离为

检验概率值为: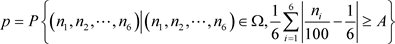
用Python语言,得概率值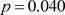 。由于
。由于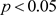 ,拒绝原假设。
,拒绝原假设。
3. 几种检验方法的效率比较
带判别函数的假设检验方法是一种一般性的方法,不同的判别函数构成不同的检验方法。上一小节的方法只是一个特例,传统的二项分布检验方法、拟合优度方法、和似然比检验方法也是这个方法的特例。本文还列举了其它判别函数的检验方法。
二项分布检验有一种精确分布计算方法。设一总体为0-1分布,其中成功的概率为p。对总体进行m次重复抽样,其中成功 次,不成功
次,不成功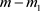 次,可以得到
次,可以得到 服从二项分布
服从二项分布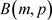 。
。
现进行假设检验,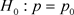 ,
,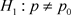 。给定显著水平
。给定显著水平 ,拒绝域为
,拒绝域为 分布中两端概率各为
分布中两端概率各为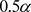 的区间。因此检验的概率值为
的区间。因此检验的概率值为 分布中
分布中 两端中概率小的一端的两倍数值,
两端中概率小的一端的两倍数值,
 (3.1)
(3.1)
当概率值小于显著水平时,就拒绝原假设,否则就接受(不拒绝)原假设。
这样定义的拒绝域有两个缺点。首先,由于二项分布左右不对称,这种两端拒绝域的概率各为 的设计不太合理,因为它的接受域的长度不是最短的。其次,这种定义不能推广的多个状态分布的假设检验,因为多项分布是多维的,不能定义各方向的极端区域概率相等。
的设计不太合理,因为它的接受域的长度不是最短的。其次,这种定义不能推广的多个状态分布的假设检验,因为多项分布是多维的,不能定义各方向的极端区域概率相等。
本文对这种检验方法做了修改,并推广到K个状态分布检验(1.2)的情形。二项分布检验只是一个特例,在此不做专门描述。先待定一个正常数c,记
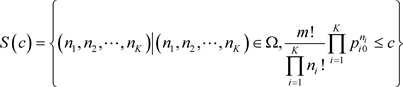 (3.2)
(3.2)
 是在样本空间中,概率小于等于c的点组成的集合。给定显著水平
是在样本空间中,概率小于等于c的点组成的集合。给定显著水平 ,假设检验的拒绝域定义为
,假设检验的拒绝域定义为
 (3.3)
(3.3)
拒绝域是在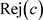 中概率小于
中概率小于 的最大集合,而接受域就是
的最大集合,而接受域就是 。
。
上述方法的判别函数为样本的概率
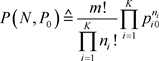 (3.4)
(3.4)
检验的概率值为概率小于等于抽到的样本概率的所有样本构成的集合的概率。
 (3.5)
(3.5)
当概率值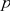 小于显著水平时,抽到的样本落在拒绝域里,因此拒绝原假设;否则就接受原假设。
小于显著水平时,抽到的样本落在拒绝域里,因此拒绝原假设;否则就接受原假设。
例1的解法2:用公式(2.5)计算检验的概率值。记抽样样本的概率为
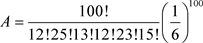
检验的概率值为:
用Python语言,得概率值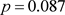 。由于
。由于 ,接受原假设。
,接受原假设。
下面说明似然比检验方法是带判别函数检验的一个特例。似然比定义为无条件的最大似然值除以在零假设限制下的最大似然值。在K个状态分布检验(1.2)中,给定样本点N,
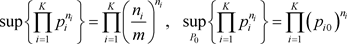 (3.6)
(3.6)
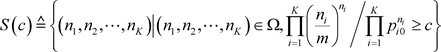 (3.7)
(3.7)
 是在样本空间中,似然比大于等于c的点组成的集合。检验的思路是,似然比越大,与无条件最大似然值相比,在零假设条件下最大似然值减少越多,零假设越不可能是真实的。
是在样本空间中,似然比大于等于c的点组成的集合。检验的思路是,似然比越大,与无条件最大似然值相比,在零假设条件下最大似然值减少越多,零假设越不可能是真实的。
给定显著水平 ,假设检验的拒绝域定义为
,假设检验的拒绝域定义为
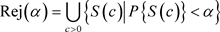 (3.8)
(3.8)
拒绝域就是在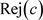 中,概率小于
中,概率小于 的最大集合,而接受域就是
的最大集合,而接受域就是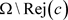 。
。
在似然比检验中,判别函数为似然比,
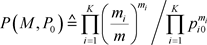 (3.9)
(3.9)
检验的概率值为似然比大于等于抽到的样本的似然比的所有样本构成集合的概率。
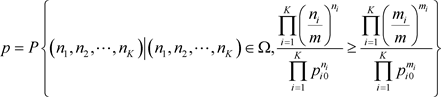 (3.10)
(3.10)
当概率值p小于显著水平时,抽到的样本点落在拒绝域里,拒绝原假设,否则就接受原假设。
例1的解法3:用公式(2.10)计算检验的概率值。记抽样样本的似然比为
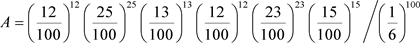
检验的概率值:
用Python语言,得概率值 。由于
。由于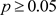 ,接受原假设。
,接受原假设。
下面说明Х2拟合优度检验是带判别函数假设检验的一个特例。在K个状态分布检验(1.2)中,拟合优度检验的Pearson Х2统计量为
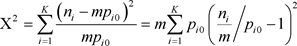 (3.11)
(3.11)
统计量可转化为该检验的判别函数
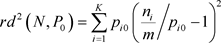 (3.12)
(3.12)
判别函数是样本频率与目标概率相对差的二阶矩。样本的判别函数越大,样本频率与目标概率相差就越大,样本与零假设就越相悖。记,
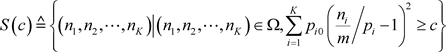 (3.13)
(3.13)
给定显著水平 ,假设检验的拒绝域定义为
,假设检验的拒绝域定义为
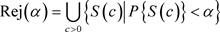 (3.14)
(3.14)
拒绝域就是在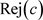 中,概率小于
中,概率小于 的最大集合,而接受域就是
的最大集合,而接受域就是 。
。
检验的概率值为判别函数大于等于抽到的样本的判别函数的所有样本构成集合的概率,
 (3.15)
(3.15)
当概率值p小于显著水平时,抽到的样本点落在拒绝域里,拒绝原假设,否则就接受原假设。
例1的解法4:用公式(2.15)计算检验的概率值。记样本频率与目标概率相对差的二阶矩为
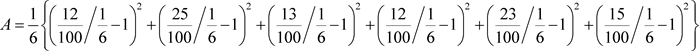
检验的概率值:
用Python语言,得概率值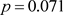 。由于
。由于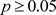 ,接受原假设。
,接受原假设。
带判别函数检验方法的函数形式是很多的。除了上述四种判别函数,本文补充两个,都是反映样本的分布频率与目标概率的差距。例如,对假设检验(1.2),判别函数可定义为样本的分布频率与目标概率的差距的二阶矩
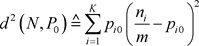 (3.16)
(3.16)
也可以定义为样本的分布频率与目标概率的差距的最大值
 (3.17)
(3.17)
不同的检验方法存在检验效率的差异,其中一个检验效率的指标是概率值。面对同一个样本,如果方法A比方法B有更小的概率值,方法A的检验效率就比方法B更高。这是因为较小的概率值更容易小于显著水平,也就更容易拒绝原假设。
针对例1这个案例,我们看到,方法1的概率值最小(为0.040),概率值小于0.05,检验拒绝了原假设。其次是方法4、方法3和方法2,其概率值分别为0.071、0.087和0.087。这三个检验的概率值都大于0.05,不能拒绝原假设。可以看到,以样本的分布频率与目标概率的距离的平均值为判别函数的检验方法,比传统的三个检验方法都更有检验效率。
4. 结论
本文引进了一种带判别函数的单样本有限状态分布检验,并给出了基于精确分布的检验计算方法。在本文方法中,给出不同的判别函数,检验可表示不同的具体检验方法,其中几个经典的检验方法,例如X2拟合优度检验、二项检验和似然比检验都是本文检验方法在不同判别函数下的特例。
主流的分布检验理论都是借用极限分布来处理的。在这个方法中,真实分布与极限分布的差异会导致检验结果出现误差,且这种误差并不能在检验中被衡量得到。由于计算机和软件的快速发展,使用精确分布处理假设检验变得越来越可行。
精确分布方法可带来两大改进。首先,该方法可以避免由分布差异导致的检验误差问题,特别是在样本量不是很大的时候。其次,在借用极限分布处理分布检验时,不同的判别函数会导致不同的极限分布,甚至有可能连极限分布都不存在。在这种情况下,判别函数的选取会受制于它的极限分布的存在性和表达形式。而在使用精确分布处理假设检验时,精确分布就是总体分布,与判别函数的选取无关。在这种情况下,我们就可以选择最大程度地表现样本频率和目标概率差异的判别函数,以提高假设检验的效率。
本文并没有从理论上给出上述六个检验方法的优劣,因此未能得出一般性结论。但针对例1这个案例,本文分析显示,以样本的分布频率与目标概率的距离的平均值为判别函数的检验方法,比传统的检验方法更有效率,这类方法值得我们进一步研究。