1. 引言
函数族的收敛性在数学和工程中扮演着非常重要的角色。
例如,用多项式逼近光滑函数(Taylor级数与幂级数),用三角函数逼近分段连续函数(Fourier级数)等,都是通过函数空间的正交基对函数进行逼近。
机器学习等领域的实践表明,映射的复合可能会带来更多的结构。
本文介绍的指数定律给出了多元映射与复合映射之间的某种同构关系:两个变量的函数可以被视为一个变量的变量函数。
在集合论、高等代数和数学分析中,指数定律的例子包括:
例1.1. 对集合 ,指数定律是指双射
,指数定律是指双射
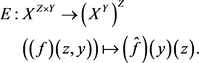
例1.2. 对于有限维线性空间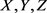 和它们之间的线性映射,有线性同构
和它们之间的线性映射,有线性同构
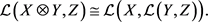
证明由 得到线性空间的同构。
得到线性空间的同构。
例1.3. 在欧氏空间 中考虑m阶连续可微函数
中考虑m阶连续可微函数 ,则对任意的
,则对任意的 ,有
,有

又由多线性性质,有

其中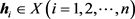 。
。
特别地,对 ,由多项式定理,有
,由多项式定理,有
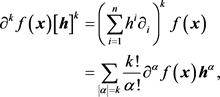
其中 为n重指标。由此可以得到Taylor定理的多元多项式表示。
为n重指标。由此可以得到Taylor定理的多元多项式表示。
上面三个例子中的映射或是不附带任何结构,或是线性映射,或与线性映射只相差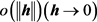 。因此应当考虑更广的一类函数,这类函数具有某种结构(如连续性),并研究这类映射的性质与映射族的收敛性。为此需要引入映射空间的拓扑结构。
。因此应当考虑更广的一类函数,这类函数具有某种结构(如连续性),并研究这类映射的性质与映射族的收敛性。为此需要引入映射空间的拓扑结构。
数学分析中主要考虑紧集上的连续函数空间。例如,有界闭区间上的连续函数列若一致收敛,则其极限函数也是连续的。这意味着有界闭区间上的连续函数全体作为某个拓扑空间中的集合是闭的。因此自然地考虑定义一致收敛度量。
一般地,需要考虑任意的拓扑空间。参考文献 [1] 中介绍了拓扑学中的基本内容。
对给定的拓扑空间可以进行大量操作,例如取乘积、商、推出等。但拓扑空间全体未必有足够好的性质,因此常只考虑某些具有特定性质的拓扑空间,例如紧致性、Hausdorff性质等。
函数空间拓扑的概念可以追溯到度量
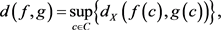
其中C是紧致空间,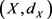 是度量空间。
是度量空间。
为了考虑C仅局部紧的情形,R. H. Fox在连续函数集 上引入了紧–开拓扑,其中Y和X是拓扑空间。对于Y中的紧集C和X中的开集U,紧–开拓扑有一个子基
上引入了紧–开拓扑,其中Y和X是拓扑空间。对于Y中的紧集C和X中的开集U,紧–开拓扑有一个子基 ,其中的元素是一些连续函数
,其中的元素是一些连续函数 ,它们满足
,它们满足 。Fox还开始研究这与“指数定律”的关系。
。Fox还开始研究这与“指数定律”的关系。
Fox给出了与指数定律类似的结果,即将例1.1中的 替换为
替换为 。这要为连续函数空间赋予拓扑。遗憾的是,人们发现这只适用于Y是局部紧的情形,即具有紧集构成的邻域基,并且需要的拓扑是紧–开拓扑。
。这要为连续函数空间赋予拓扑。遗憾的是,人们发现这只适用于Y是局部紧的情形,即具有紧集构成的邻域基,并且需要的拓扑是紧–开拓扑。
关于指数定律,R. Arens和J. Dugundji给出了 中拓扑的详细分析。
中拓扑的详细分析。
指数定律的有效性对局部紧空间的限制对于拓扑学来说是困难的。E. Spanier在参考文献 [2] 中提出,这种情况可以通过使用“准拓扑空间(quasi-topological spaces)”来改善,该空间由从紧Hausdorff空间C上的一族映射 确定了X,还满足特定的公理。在这之后,参考文献 [3] 也对其进行了讨论。
确定了X,还满足特定的公理。在这之后,参考文献 [3] 也对其进行了讨论。
Hausdorff紧生成空间最初称为k-空间,来源于德语单词kompakt。Hurewicz对k-空间进行了研究。其他数学家如Kelley、Dugundji、Félix、Halperin和Thomas也发现了它们。
20世纪60年代,他们进行深入研究的动机来自于常见拓扑空间类别的众所周知的缺陷:这不是笛卡儿闭范畴,通常笛卡儿积的识别映射并不总是识别映射。有两种方法可以改善这种情况。一是限制在Hausdorff紧生成的Hausdorff空间的全子范畴内,这实际上是笛卡尔闭的。另一种是考虑通常的Hausdorff空间,但使用紧致子集上的连续函数。
R. Brown在参考文献 [4] 中发现,在具有Hausdorff性质的k-空间和连续映射的范畴中,指数定律是满足的。参考文献 [5] 指出,这一类别“可能对拓扑的所有目的都是充分和方便的”。而参考文献 [6] 中的论述提出了Hausdorff空间和

的定律,解释了指数定律不能在所有空间中存在。
可以通过将紧生成表示为“具有关于紧Hausdorff空间到空间的所有映射的最终拓扑”将Hausdorff条件移除。在参考文献 [7] 中,这被推广到紧Hausdorff空间的特定集族 的情况,考虑拓扑空间之间的
的情况,考虑拓扑空间之间的 -连续映射
-连续映射 ,其上赋予了以
,其上赋予了以

为子基的拓扑,其中U是Y中的开集,而 是“测试”映射。
是“测试”映射。
这些观点可以推广到非Hausdorff情形,例如紧生成的空间。这是因为Hausdorff空间的标识空间不必是Hausdorff。
在现代代数拓扑中,该性质通常与弱Hausdorff性质结合。弱Hausdorff性质这一概念是由M. C. Cord引入的,以弥补使用Hausdorff空间范畴带来的不便。其讨论在参考文献 [8] 中。
本文用了对角映射和对角集证明弱Hausdorff的性质,而对角集的作用在其他地方也有体现,为此本文还介绍了滤子基。
序列足以描述度量空间中的拓扑性质,或者更一般地,描述拓扑具有可数基的拓扑空间中的拓扑性质。然而,在更抽象的空间中需要滤子基或网。
滤子的研究是描述一般拓扑空间收敛性的一种非常自然的方法。滤子于1937年由Cartan引入。在Kowalsky的文献中可以看见拓扑的发展对滤子的影响。滤子也是泛函分析中描述非拓扑收敛概念的重要工具。此外,Preuss在他关于分类拓扑的书中应用了滤子。
在拓扑空间中,滤子可以用于刻画连续性、紧性等重要概念。本文将采用滤子基说明对角集的应用。
此外,关于滤子和滤子基的许多性质可以在参考文献 [9] 中找到。
本文中对拓扑空间的一个重要操作是k化。而本文中定义的k化是给空间赋予某个终拓扑,这是基于如下一系列事实:
终拓扑是拓扑空间上使所有测试函数连续的最细拓扑。商空间上的商拓扑是关于单个满射函数的终拓扑,即商映射。不相交并拓扑是关于包含映射的终拓扑。终拓扑也是拓扑空间范畴中每个直接极限所赋予的拓扑。拓扑与一些子空间集合是一致当且仅当拓扑是由自然包含诱导的终拓扑。
关于终拓扑的详细讨论和例子见参考文献 [10] [11] [12] 。
本文由k化入手定义k-空间,其中k化是给空间赋予终拓扑,接下来本文依次定义了k-映射,并对k-映射全体赋予了测试–开拓扑,使之成为k-映射空间。
在上述定义下,本文证明了指数定律。
接下来本文还介绍弱Hausdorff性质。在k-空间和弱Hausdorff性质的判定中,都出现了对角集。从滤子基的角度可以看到对角集在定义度量空间中函数的一致连续时起到的作用。
在本文的最后,将把含参积分作为k-空间中的例子讨论其性质。为了一般化,本文利用滤子基直接将定义域推广到 。在证明含参积分对参数的连续性时,通过一致连续的滤子基定义再次用到了对角集。
。在证明含参积分对参数的连续性时,通过一致连续的滤子基定义再次用到了对角集。
本文的主要结果是给出k-映射的指数定律的一个证明,并举出了一个k-空间的具体例子,展示了对角集在k-空间判定和含参积分中的应用。
2. 相关理论基础和模型
2.1. 积空间与映射空间
首先敘述积空间与映射空间的概念和性质。
定义2.1. 设 是一族集合。对J-元组
是一族集合。对J-元组

定义投影映射

定义2.2. 设 是一族拓扑空间,对每个
是一族拓扑空间,对每个 定义
定义 的子集族
的子集族

则 导出的拓扑
导出的拓扑 称为积拓扑。称
称为积拓扑。称

为积空间,其中每个 称为坐标空间。
称为坐标空间。
推论2.1. 积空间到坐标空间的投影映射是连续映射。
定义2.3. 对从J到Y的映射全体

称其中的元素 为选择函数。
为选择函数。
假设(选择公理)。设 为某一集合的子集族。若
为某一集合的子集族。若 ,且
,且 ,则
,则

即选择函数存在。
积空间有以下三个性质,证明见点集拓扑教科书,例如参考文献 [1] 。
引理2.1. 映射 连续当且仅当对任意
连续当且仅当对任意 ,有
,有 连续。
连续。
引理2.2. 积空间保持连通性和Hausdorff性。
引理2.3 (Tychonoff)。积空间保持紧致性。
定义2.4. 设X是集合, 是拓扑空间,则称
是拓扑空间,则称

导出的拓扑为 -开拓扑。
-开拓扑。
定义2.5. 称映射

为赋值映射。
2.2. 度量空间
实际应用中,常考虑度量空间。这里列出本文将用到的度量空间中的性质,许多点集拓扑学的教科书中都有它们的证明,例如参考文献 [1] 。
引理2.4. 给定集合X上的度量d,定义标准有界度量 ,则d与
,则d与 诱导相同的拓扑。
诱导相同的拓扑。
度量空间中可以定义收敛和一致收敛。而从点集拓扑学中知道,与一致收敛对应的还有等度连续。
定义2.6. 设 为度量空间,
为度量空间, ,若对任意
,若对任意 ,存在
,存在 的邻域U,对任意
的邻域U,对任意 和任意
和任意 ,有
,有 ,则称
,则称 在
在 等度连续。又若
等度连续。又若 在x处等度连续对任意的
在x处等度连续对任意的 成立,则称
成立,则称 等度连续。
等度连续。
完备度量空间具有更好的性质,并且给定度量空间时,完备化是唯一的。
定义2.7. 设X是度量空间, 是完备度量空间,若X与
是完备度量空间,若X与 的一个稠密子集
的一个稠密子集 等距同构,则称
等距同构,则称 是X的一个完备化。
是X的一个完备化。
引理2.5. 等距同构意义下,每个度量空间的完备化是唯一的。
这一引理在泛函分析或点集拓扑学中都会用到,参考文献有 [1] [12] 。特别地,在映射的陪域是度量空间的情形下,还能为映射空间赋予度量。
定义2.8. 设X为拓扑空间, 为度量空间,任意给定映射
为度量空间,任意给定映射 ,X的紧致子集C和
,X的紧致子集C和 ,称
,称

生成的拓扑为紧收敛拓扑。
例2.1. 设X为拓扑空间, 为度量空间,
为度量空间, ,赋予紧收敛拓扑,则有:
,赋予紧收敛拓扑,则有: 等价于对X的任意紧致子集C,有
等价于对X的任意紧致子集C,有 一致收敛于
一致收敛于 ,其中
,其中 表示限制。
表示限制。
2.3. 滤子基上的收敛
绪论中已经简要介绍了滤子基,数学分析中的相关定理也可以用滤子基的语言证明。参考文献 [13] [14] 中给出了许多对许多在数学分析中实用的滤子基,并对滤子基的各项性质进行了证明。下面举出在本文的例子中会用到的滤子基。
定义2.9. 若集合族 满足:
满足: ,且有
,且有

则称 为X上的一个滤子基。
为X上的一个滤子基。
定义2.10. 设X是集合, 是滤子基。若满足
是滤子基。若满足

则称 比
比 细。
细。
例2.2.在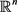 中考虑
中考虑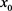 的邻域和去心邻域,可以得到两个滤子基
的邻域和去心邻域,可以得到两个滤子基
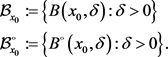
例2.3. 设
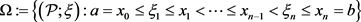
为带标记的有限分划的集合,则
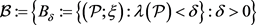
是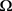 上的滤子基。
上的滤子基。
例2.4. 设X为拓扑空间, 是
是 的邻域基,则
的邻域基,则 也构成X上的一个滤子基。
也构成X上的一个滤子基。
反之,给定滤子基,将其作为邻域基也可生成一个拓扑。
定义2.11. 设Y是拓扑空间,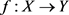 ,
, 是X上的滤子基,若对
是X上的滤子基,若对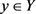 的任一邻域V,存在
的任一邻域V,存在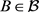 使得
使得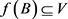 ,则称y为f在
,则称y为f在 上的极限,记为
上的极限,记为

特别地,本文的例子中考虑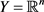 的情形,此时滤子基上的极限具有唯一性,局部有界性和保序性,且保持四则运算。
的情形,此时滤子基上的极限具有唯一性,局部有界性和保序性,且保持四则运算。
定理2.1 (Cauchy准则)。设 是完备度量空间,则f在
是完备度量空间,则f在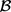 上极限存在当且仅当
上极限存在当且仅当
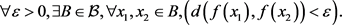
下面可以用滤子基的语言刻画连续性。
引理2.6. 对任意函数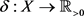 ,定义
,定义

则集族
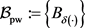
构成滤子基。
定理2.2. 设 是度量空间,则
是度量空间,则 连续当且仅当
连续当且仅当

为了描述一致连续性,需要引入更多度量。
定义2.12. 在 上定义度量
上定义度量
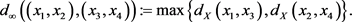
对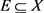 ,定义
,定义
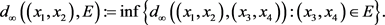
定义2.13. 称
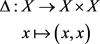
为对角映射。称 为对角集。
为对角集。
对角映射和对角集的作用在后面将会多次看到。
引理2.7. 对任意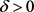 ,定义
,定义

则 构成滤子基。
构成滤子基。
定理2.3. f在X上一致连续当且仅当
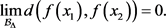
推论2.2. 比
比 细,即按点连续是一致连续的必要条件。
细,即按点连续是一致连续的必要条件。
定理2.4. 设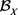 与
与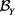 是滤子基,则
是滤子基,则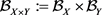 是滤子基。
是滤子基。
这一性质意味着相对于网,滤子基可以更方便地处理多变量情形。
参考文献 [9] [13] [14] 中介绍了更深入的内容和许多例子。
2.4. 极限的换序
数学分析中常会遇到极限换序的问题,例如函数列的连续性、含参积分的连续性等。一致收敛给出了极限换序的充分条件。
定义2.14.设 为集合,
为集合, 为Y上的滤子基,
为Y上的滤子基,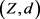 为完备度量空间,
为完备度量空间, 。若对任意
。若对任意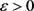 ,存在
,存在 ,对任意
,对任意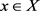 和
和 ,都有
,都有 ,则称
,则称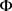 在X上沿
在X上沿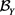 对x一致地收敛到
对x一致地收敛到 ,记为
,记为
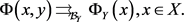
定理2.5. (一致收敛的Cauchy准则)。
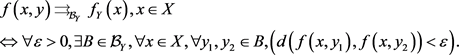
定理2.6. 设 为集合,
为集合, 为完备度量空间,
为完备度量空间, 分别为
分别为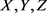 上的滤子基。若
上的滤子基。若 和
和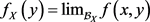 都存在,且其中至少一个是一致的,则
都存在,且其中至少一个是一致的,则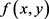 的两个累次极限和重极限均存在且相等。
的两个累次极限和重极限均存在且相等。
证明 不妨设 ,则由一致收敛的定义,存在
,则由一致收敛的定义,存在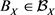 ,当
,当 ,对任意的
,对任意的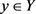 ,有
,有 。
。
由于 ,取定
,取定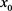 ,则由Cauchy准则,存在
,则由Cauchy准则,存在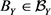 ,有
,有

下一步是证明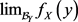 存在:取
存在:取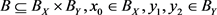 ,则有
,则有
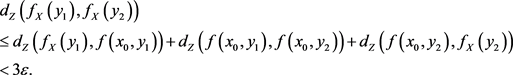
由Cauchy准则知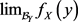 存在,记为A。
存在,记为A。
接着证明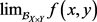 存在且等于A:由
存在且等于A:由 的定义,注意到
的定义,注意到

即得证。
最后可以证明 存在且等于A:由
存在且等于A:由 存在和
存在和 存在,命题得证。
存在,命题得证。
由此可以看到一致收敛和等度连续在滤子基的视角下是完全对称的。
3. k-映射的指数定律
3.1. k-映射和k-映射空间
本文将通过k化定义k-空间,而k化是给空间赋予终拓扑。
定理3.1. 给定一族拓扑空间 ,一个集合Y和X上一族映射
,一个集合Y和X上一族映射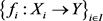 ,则Y上存在一个拓扑
,则Y上存在一个拓扑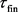 ,使得对任意拓扑空间Z,及映射
,使得对任意拓扑空间Z,及映射 ,有g连续当且仅当对任意的
,有g连续当且仅当对任意的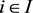 ,有
,有 连续,并且
连续,并且 还是满足这一条件的最细的拓扑。称
还是满足这一条件的最细的拓扑。称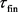 为Y关于
为Y关于 的终拓扑。
的终拓扑。
证明 考虑集族
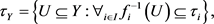
显然 。设
。设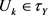 。由原像的性质,对任意的k有
。由原像的性质,对任意的k有

对有限的k有

因此 是一个拓扑。
是一个拓扑。
由连续映射的定义,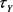 是满足终拓扑条件最细的拓扑,因此
是满足终拓扑条件最细的拓扑,因此 即为所求。
即为所求。
推论3.1. 若为Y赋予关于 的终拓扑,则
的终拓扑,则 均是连续的。
均是连续的。
证明 由连续映射的定义即得。
定义3.1. 对拓扑空间X和任意紧Hausdorff空间C,为X赋予关于连续映射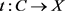 的终拓扑,记为kX,称为k化。若
的终拓扑,记为kX,称为k化。若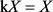 ,则称X为k-空间或紧生成空间,记为CG。称C为测试空间,其上的映射t称为测试映射。
,则称X为k-空间或紧生成空间,记为CG。称C为测试空间,其上的映射t称为测试映射。
显然kX (未必严格地)细于X,并且有:
推论3.2.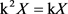 。
。
证明 k-空间具有终拓扑,它是最细的,因此k-空间的k化不会给拓扑增加更多开集。
直接根据定义判定一个空间是否是k-空间很不方便,引入k-闭这一概念后,就可以利用起具有更多性质的测试空间。
定义3.2. 设X是拓扑空间, ,如果对任意紧Hausdorff空间K以及任意连续映射
,如果对任意紧Hausdorff空间K以及任意连续映射 ,有
,有 在K中闭,则称A在X中k-闭。
在K中闭,则称A在X中k-闭。
定理3.2. X是k-空间等价于X中的k-闭子空间是闭的。
证明对任意测试空间C,集合 及连续映射
及连续映射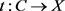 ,X具有关于t的终拓扑等价于
,X具有关于t的终拓扑等价于
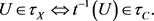
当 取X的k-闭子空间时就得到了结论。
取X的k-闭子空间时就得到了结论。
有了上面这一定理,就可以利用原像在测试空间中的性质更方便地判定k-空间。
定理3.3. 局部紧Hausdorff空间是k-空间。
证明设X是局部紧Hausdorff空间,K是X的k-闭子空间。下证K是闭的。
设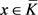 ,由于已知X是局部紧Hausdorff空间,存在x的邻域U使得
,由于已知X是局部紧Hausdorff空间,存在x的邻域U使得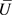 是紧Hausdorff的,因此
是紧Hausdorff的,因此 。又由于K是k-闭的,考虑包含映射
。又由于K是k-闭的,考虑包含映射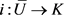 知
知 在
在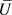 中闭,得到
中闭,得到 。
。
定理3.4. 设X是k-空间,Y是任意拓扑空间,则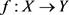 连续当且仅当
连续当且仅当 连续。
连续。
证明 由连续映射的定义得到充分性。
反之,设K为Y的k-闭子空间, 是测试映射。
是测试映射。 也是测试映射,有
也是测试映射,有
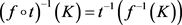
在C中闭。故 在X中k-闭,因此闭,由连续映射的定义得到
在X中k-闭,因此闭,由连续映射的定义得到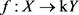 连续。
连续。
定义3.3. 对任意拓扑空间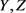 ,定义
,定义
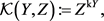
其中的元素称为从Y到Z的k-映射。
这一定义表明,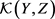 中的元素实际上取自
中的元素实际上取自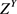 中那些在复合了测试映射
中那些在复合了测试映射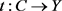 后就能成为
后就能成为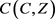 中元素的映射。
中元素的映射。
例3.1. 恒等映射 是k-映射,但未必是连续映射。
是k-映射,但未必是连续映射。
例3.2. 若 是k-映射,则
是k-映射,则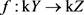 是连续映射。
是连续映射。
对于拓扑空间之间的k-映射,可以定义其映射空间中的拓扑。
定义3.4. 对拓扑空间Y,拓扑空间 ,测试空间C和测试映射
,测试空间C和测试映射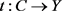 ,定义
,定义
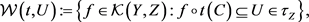
其导出的拓扑称为k-映射空间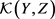 上的测试–开拓扑。
上的测试–开拓扑。
接下来假设每个k-映射空间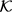 中的拓扑都是测试–开拓扑
中的拓扑都是测试–开拓扑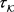 。
。
至此写出指数定律所需要的各个定义都已经给出。
例3.3. 若Y为Hausdorff空间,则依此定义得到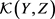 上的紧–开拓扑。
上的紧–开拓扑。
3.2. 指数定律
在集合的指数定律中,只需考虑元素的对应,因此指数映射的定义是自然的。然而,尝试在k-映射空间中定义“指数映射”时需要处理三个问题:
第一,将k-映射经过“指数映射”之后,是否还能得到k-映射?
第二,“指数映射”涉及多个k-映射空间,对它们k化时,不同的k化次数是否不会影响积空间的拓扑?
第三,“指数映射”是否保持了拓扑性质,即“指数映射”是不是同胚?
下面将看到,在k-映射空间中,这些问题都有肯定的答案。
首先证明将k-映射经过“指数映射”之后,得到的仍然是k-映射。
定理3.5. 设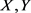 和Z为拓扑空间,
和Z为拓扑空间, ,则
,则 。
。
证明设 是测试映射,则
是测试映射,则 也是测试映射。因此
也是测试映射。因此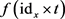 连续,
连续,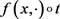 连续,由k-映射的定义得到
连续,由k-映射的定义得到 。
。
引理3.1. 对任意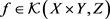 ,定义
,定义

则有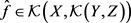 。
。
证明只要证明对任意测试映射 ,有
,有 连续。
连续。
设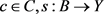 是测试映射,
是测试映射, 是
是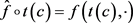 在
在 中的邻域。由于
中的邻域。由于 也是测试映射,
也是测试映射,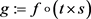 连续。而
连续。而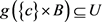 ,即
,即 ,c有开邻域V使得
,c有开邻域V使得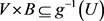 。因此
。因此 ,即
,即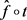 连续。
连续。
引理3.2. 设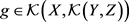 ,定义
,定义

则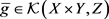 。
。
证明 设 是测试空间,
是测试空间,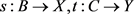 是测试映射。考虑交换图
是测试映射。考虑交换图


由于 都连续,
都连续, 也连续。因此
也连续。因此 。
。
有了以上两个引理,才可以放心地定义指数映射:
定理3.6. 对任意拓扑空间 和Z,有良定双射
和Z,有良定双射

证明 即为所求。
即为所求。
此时的指数映射只是集合意义上的映射,其对拓扑的影响仍然未知。
接下来处理第二个问题。
定理3.7. 设Y和Z为拓扑空间, 为测试映射,则
为测试映射,则

是连续映射。
证明 设 ,
, ,V为
,V为 的一个开邻域。
的一个开邻域。
由于 连续,存在c的开邻域U使得
连续,存在c的开邻域U使得 。由于测试空间C是局部紧的,存在c的紧致邻域B满足
。由于测试空间C是局部紧的,存在c的紧致邻域B满足 。
。
定义 ,则s是测试映射,且
,则s是测试映射,且 ,因此
,因此 连续。
连续。
推论3.3. 若Y是局部紧Hausdorff空间,则赋值映射 是连续映射。
是连续映射。
定理3.8. 设 ,则
,则 当且仅当对任意测试映射
当且仅当对任意测试映射 和
和 ,有
,有

连续。
证明 充分性:设D为测试空间, 是测试映射,下证
是测试映射,下证 连续。
连续。
设 。则
。则

其中 为对角映射。由于
为对角映射。由于 和
和 都连续,得到
都连续,得到 连续。
连续。
必要性:若 都为测试映射,则
都为测试映射,则 也为测试映射,命题得证。
也为测试映射,命题得证。
作为推论,至此第二个问题也可以得到肯定的回答。
推论3.4. 设 为拓扑空间,则有
为拓扑空间,则有 。
。
证明 由于 和
和 都连续,得到
都连续,得到

连续。因此

连续。
设 是测试映射,则
是测试映射,则

都是测试映射。因此

连续。
综上, 。
。
由以上推论知,先k化,做笛卡尔积后再次k化得到的拓扑与直接笛卡尔积后再k化得到的拓扑是相同的,因此可以定义k-空间的乘积:
定义3.5. 对k-空间Y和Z,定义

定义3.6. 对任意拓扑空间Y和Z,定义

有了前面的铺垫,最终可以证明E就是本文想要得到的“指数映射”,它不仅是集合意义上的映射,还是同胚,保持了拓扑性质。
定理3.9 (指数定律)。对任意k-空间 和Z,映射空间赋予测试–开拓扑,则有如下同胚:
和Z,映射空间赋予测试–开拓扑,则有如下同胚:

证明 定义映射

其中 。E是良定的双射。
。E是良定的双射。
考虑映射

和赋值映射

有 ,因此E连续。
,因此E连续。
考虑

有

是连续映射。由于 ,
, 连续。
连续。
综上,E是同胚映射。
4. 具有弱Hausdorff性质的k-空间
4.1. 弱Hausdorff性质
一些参考文献,例如 [11] [15] 中,k-空间会与弱Hausdorff性质一起出现。在此先给出它的定义。
定义4.1. 若对任意紧Hausdorff空间K以及任意连续映射 ,有
,有 闭,则称X是弱Hausdorff空间,记为WH。记弱Hausdorff的紧生成空间为CGWH (即弱Hausdorff的紧生成空间,compactly generated weakly Hausdorff spaces)。
闭,则称X是弱Hausdorff空间,记为WH。记弱Hausdorff的紧生成空间为CGWH (即弱Hausdorff的紧生成空间,compactly generated weakly Hausdorff spaces)。
弱Hausdorff性质介于 和Hausdorff性质之间。有下面两个定理:
和Hausdorff性质之间。有下面两个定理:
定理4.1. 弱Hausdorff空间是 空间。
空间。
证明 只要证弱Hausdorff空间中的单点集是闭集。取定义中的紧Hausdorff空间K为单点集就得到了证明。
定理4.2. Hausdorff空间是弱Hausdorff空间。
证明 设X是Hausdorff空间, 同弱Hausdorff空间的定义,则由定义知
同弱Hausdorff空间的定义,则由定义知 是X的紧子集,因此闭。
是X的紧子集,因此闭。
下面这个例子说明弱Hausdorff空间未必是Hausdorff空间。
例4.1. 的单点紧化是弱Hausdorff空间,但不是Hausdorff空间。
的单点紧化是弱Hausdorff空间,但不是Hausdorff空间。
与关注原像性质的k-闭相反,弱Hausdorff空间中,像的性质被保留。
定理4.3. 若X是WH,则对任意紧Hausdorff空间K以及连续映射 ,有
,有 紧致且Hausdorff。
紧致且Hausdorff。
证明 连续映射保持紧致性,因此 紧。
紧。
设 ,则
,则 是不相交的闭集。因此有不交的开集
是不相交的闭集。因此有不交的开集 使得
使得

则 给出了
给出了 的不交的开邻域。
的不交的开邻域。
推论4.1. 若X是WH,则: 是k-闭的当且仅当A与X的任意紧子空间的交是闭的。
是k-闭的当且仅当A与X的任意紧子空间的交是闭的。
定理4.4. 设X是CGWH, 是映射,且对任意紧子空间
是映射,且对任意紧子空间 ,有
,有 连续,则f连续。
连续,则f连续。
证明 设 ,由于
,由于

得 ,因此f连续。
,因此f连续。
定理4.5. 若X是k-空间,则X是WH当且仅当对角集 在
在 中是闭的。
中是闭的。
证明 设K是紧Hausdorff空间。
必要性:设 是两个测试映射,记
是两个测试映射,记


f也是测试映射。L紧致且Hausdorff,因此 是
是 的紧Hausdorff子空间,在
的紧Hausdorff子空间,在 中是闭的。
中是闭的。 在K中闭,因此
在K中闭,因此

在 中闭。
中闭。
充分性:设f是测试映射。只要证 在X中k-闭。设
在X中k-闭。设 是测试映射,则
是测试映射,则

也是测试映射。因此

在 中闭,故紧致。进一步有
中闭,故紧致。进一步有

在C中紧致,故闭。即 在X中k-闭。
在X中k-闭。
在这一定理的证明中,对角集再次起到了作用。对角集可以被用来判定Hausdorff性质,例如参考文献 [16] 。这也体现了弱Hausdorff性质与Hausdorff性质的相似之处。
例4.2. 若X是CGWH, 是度量空间,则
是度量空间,则 在紧收敛拓扑下是
在紧收敛拓扑下是 中的闭集。
中的闭集。
参考文献 [1] 中有关于这一例子的详细讨论。
4.2. 例子:含参积分
数学分析中主要考虑 的情形,而
的情形,而 是局部紧Hausdorff空间,因此也是k-空间。
是局部紧Hausdorff空间,因此也是k-空间。
下面以 中的含参黎曼积分作为k-映射空间中的具体例子。
中的含参黎曼积分作为k-映射空间中的具体例子。
定义4.2. 设 为若尔当可测闭区域,T为集合,
为若尔当可测闭区域,T为集合, 满足对任意
满足对任意 ,有
,有 是D上的黎曼可积函数,则可定义含参积分
是D上的黎曼可积函数,则可定义含参积分

定理4.6. 设 为若尔当可测闭区域,
为若尔当可测闭区域, 为开集,
为开集, ,则
,则 。
。
证明 对任意 ,取
,取 的紧致邻域
的紧致邻域 ,则f在
,则f在 上一致连续。因此对任意
上一致连续。因此对任意 ,存在
,存在 ,使得当
,使得当 时有
时有 。取
。取 ,有
,有

其中 表示D的若尔当测度,是常数。
表示D的若尔当测度,是常数。
此定理的证明完全采用数学分析的语言,但从一致连续性的滤子基定义中可以看到,这一证明实际上用到了对角映射。
5. 总结与展望
本文首先以数学分析和高等代数中的直观例子引入了指数定律。接着介绍了相关理论基础和模型,并通过终拓扑定义的k化定义了k-映射。而为了使k-映射全体构成拓扑空间,本文定义了测试–开拓扑。
为了证明k-映射的指数定律,给出了多元映射与复合映射之间的关系。对k-映射而言,经过k化后的多元映射空间与多重映射空间是同胚的,且有着具体的对应方式。
此外,由于k-映射常与弱Hausdorff性质共同起作用,本位还介绍了弱Hausdorff性质。而在弱Hausdorff性质中,对角集在判定时起到了重要作用。
由于度量空间是k-空间,其上的连续映射空间在紧收敛拓扑下构成了闭集。对角集可以应用于一致连续的一般定义。在CGWH的判定中还通过对角集体现了弱Hausdorff性质与Hausdorff性质的相似之处。
本文最后用证明了数学分析中含参积分对参数的连续性,给出了k-空间的一个例子。用滤子基的语言可以更清晰地看到,对角集在一致连续中起到的作用。
指数律结果的一个重要推广涉及闭子集上的部分映射空间。与此相关的一个有用的技巧是此类部分映射的可表示性,这一思想来自以下结果:
具有闭域的部分映射集 与
与 是双射的,其中
是双射的,其中 ,且C在
,且C在 中闭当且仅当C在X中闭或
中闭当且仅当C在X中闭或 ,即
,即 在
在 中开但不闭。
中开但不闭。
在参考文献 [17] 中给出了更多相关的讨论。
还有基于其他类型的 -开拓扑和基于图拓扑的方法,以此类应用为目的的结果可以在参考文献 [18] [19] 中找到。
-开拓扑和基于图拓扑的方法,以此类应用为目的的结果可以在参考文献 [18] [19] 中找到。
参考文献 [20] [21] 中有关于k-空间的更多讨论。k-映射和k-空间还可以用于处理微分方程对参数的依赖性,参考文献 [22] 中给出了一系列定理和例子。
指数定律还有其它形式,例如参考文献 [23] 。
关于拓扑空间中滤子的作用,参考文献 [24] 对其作了介绍。
进一步,用范畴的语言还可以揭示CGWH空间全体具有的泛性质。参考文献 [25] - [32] 等对范畴语言下的CGWH进行了讨论。
相对于Hausdorff性质,具有弱Hausdorff性质的紧生成空间全体在范畴论中具有更好的性质。
记紧生成弱Hausdorff拓扑空间的范畴为CGWH,记紧生成Hausdorff拓扑空间为CGH。两者都是拓扑空间的实用范畴(convenient category),这一概念见参考文献 [32] 。
然而,CGWH还有一个进一步的关键属性:推出结构在CGWH中的表现优于CGH,具体地,CGWH在推出下是闭的,而CGH并没有这么好的性质。参考文献 [33] 中提供了更多相关内容。
致谢
本文的最初想法源自我的读书笔记,但想要将其整理成论文是远远不够的。疫情期我由于管控措施不能返校,这导致本文写作过程中曾进度缓慢。
在此郑重感谢我的指导老师——南京工业大学数理科学学院副院长马树建教授。
无论是课题的学习、研究,还是写作、格式修改等方面,马老师都给予了我宝贵的支持,尤其是在科研上的高超洞察力帮助我迅速理清了论文的思路。疫情期间,马老师根据实际情况通过线上或线下方式与我交流并对我进行指导。正因为这些交流和指导,我才能最终完成这篇论文。在学习、科研的方方面面,马老师对我的教诲我都将铭记在心。
在教科研工作的百忙之中,马老师还不时关心我的学习和生活,让我在疫情期间也能保持良好的生活态度。平时马老师散发的人格魅力也在潜移默化中让我有了更好的心态面对遇到的困难和挫折。
最后,再次向马老师致以衷心的感谢、真诚的敬意和美好的祝福!
基金项目
本研究为国家级大学生创新创业训练项目成果(项目编号:202010291082Z)。